基于深層神經網絡的雷達波形設計

趙俊龍， 李 偉， 王泓霖， 鄒 鯤

(空軍工程大學信息與導航學院， 西安， 710077)

雷達是現代戰爭不可或缺的探測工具，歷次戰爭都證明具有良好目標探測與識別能力的雷達對戰爭態勢的塑造具有決定性作用。雷達通過接收和處理目標反射的電磁波來獲取目標信息，其發射波形關系到反射波中包含信息的多少，因此，發射波形對雷達性能有重要影響。雷達波形設計方法多種多樣，其中，SNR準則和MI準則是雷達波形設計中常用的兩種設計準則。Pillai[1]首次提出最大化雷達接收信號的信噪比來設計波形，提高了雷達目標檢測能力，但其產生的波形往往將能量聚集在雷達工作頻帶的某一頻段，減縮了雷達正常工作帶寬，降低雷達分辨率[2]。Bell[3]提出最大化回波信號與目標沖激響應間的互信息量來設計波形，降低了目標響應不確定性，然而該方法將更多的能量置于互信息量更高的頻點，制約了雷達其他性能。Romero[4]針對確定目標和隨機目標分別采用SNR與MI準則設計波形，并推導出兩準則之間關系。胡旭[5]提出了一種聯合準則，通過最大化信噪比與互信息之間的差異來設計波形。在此基礎上，本文基于多準則聯合優化思想，聯合SNR與MI準則設計波形。

近年來深度學習成為研究熱門，其可有效提取數據高維特征，在圖像處理、語音識別、機器翻譯、自動駕駛[6]等領域幫助人類取得了前所未有的成就，同時在雷達領域也得到了廣泛應用[7-9]，例如基于深度學習的SAR圖像目標檢測[10]和識別[11]，基于深度學習的SAR地物分離以及深度學習在多普勒雷達身體姿態感知中的應用[12]。然而深度學習目前在雷達領域主要應用于雷達目標識別，并未涉及雷達波形設計。

雷達根據任務類型選擇不同波形設計準則，進行參數估計時常用MI準則，針對目標檢測則常用SNR準則[13]。基于上述單一準則的波形設計方法，會在提高某個指標的同時影響其他指標，無法兼顧檢測性能和參數估計性能；如果聯合2個準則，則面臨目標函數難于建立的問題。而DNNs具有極強數據內在規律學習能力，可將不同數據的內在規律提取、綜合，達到數據特征融合的目的。利用DNNs對復雜數據規律的學習能力，將SNR與MI準則生成信號的內在規律進行提取、融合，兼顧兩種準則信號產生方式，進而達到聯合目的。

基于上述聯合思想及DNNs對數據內在規律的學習能力，本文提出一種基于深層神經網絡的雷達波形設計方法，利用DNNs將SNR和MI準則聯合起來設計波形。首先設定環境變量，根據SNR與MI準則分別進行波形設計，產生相應數據；其次將SNR與MI準則生成信號進行混合且與其對應的環境變量共同組成訓練集，并對DNNs進行訓練；最后將另一部分由MI準則產生數據與其對應環境信息一起構成測試集，進行測試。

1 雷達信號模型與深層神經網絡基本原理

1.1 雷達信號模型

信號模型見圖1所示，設x(t)為雷達發射信號，n(t)為雷達接收機噪聲，目標沖激響應h(t)為定義在區間[0,Th]中的一個隨機過程，c(t)為信號雜波沖激響應，y(t)是雷達接收機接收信號，f(t)為理想低通濾波器的系統響應。x(t)的傅里葉變換為X(f)，n(t)的功率譜密度為Snn(f)，且h(t)的傅里葉變換為H(f)，c(t)的功率譜密度為Scc(f)。由圖1可知：

y(t)=f(t)[x(t)h(t)+x(t)c(t)+n(t)]

(1)

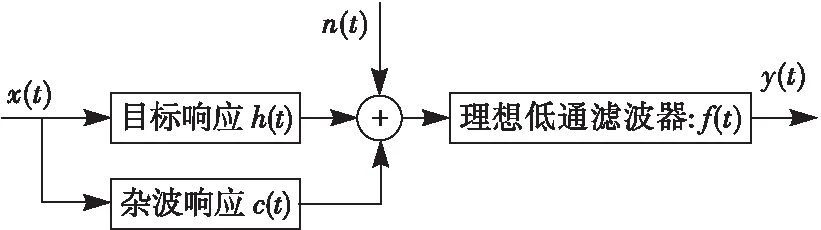
圖1 隨機擴展目標信號模型

雷達波形設計中常用兩種設計準則[4]，即MI準則和SNR準則：

(2)

MI =I(y(t)；h(t)|x(t))=

(3)

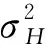
1.1.1 SNR準則

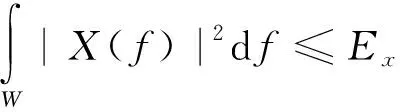
|X(f)|2=max[0,B(f)(A-D(f))]

(4)

式中：B(f)和D(f)分別為：

(5)

(6)

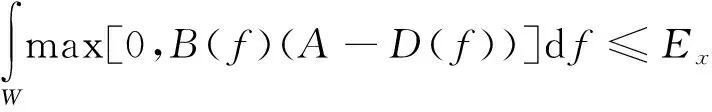
1.1.2 MI準則

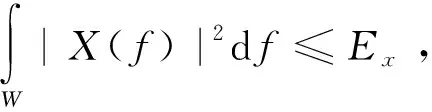
|X(f)|2=

(7)

式中：

(8)

(9)

(10)

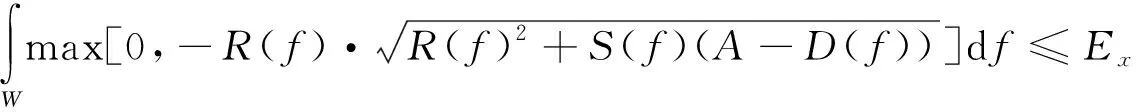
1.2 深層神經網絡基本原理

早在20世紀40年代，心理學家McCulloch和數理邏輯學家Pitts就提出了一種MP神經網絡模型，該模型實際上只是單個神經元的數學描述，開啟了神經網絡研究的大門。2006年，Hinton提出了深度置信網絡以及快速學習算法，拉開深度學習大幕。隨著近年來在大量數據驅動下，神經網絡已經發展出諸多變體，學術界迎來了研究神經網絡的熱潮。

神經元是由輸入、輸出以及計算單元組成的自適應非線性模型，人工神經網絡(Artificial Neural Network，ANN)由眾多神經元組成，具有刻畫輸入數據與對應輸出數據之間復雜非線性關系的能力[14]。一般具有輸入層、隱藏層、輸出層3層結構，每層輸出端設置相應激活函數，層與層之間具有相應權值。數據由輸入層進入神經網絡，神經網絡中每個神經元將其接收到的數據進行疊加，并將其與該神經元對應偏置之和經由激活函數處理后輸出。經過網絡中所有神經元的處理之后可得神經網絡的輸出。理論上，只要隱藏層神經元數量足夠多，單隱層神經網絡便可以無限逼近任何函數[15]。然而，為提高網絡對數據特征的刻畫能力，通常增加隱藏層的數量，這樣就得到了DNNs，其結構見圖2。

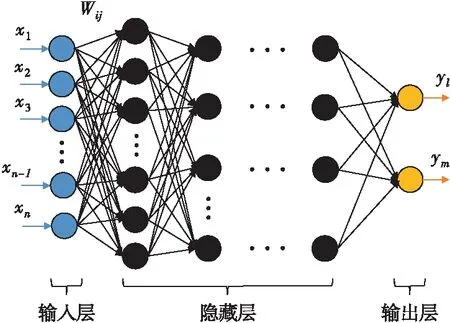
圖2 深層神經網絡

(11)

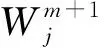
2 基于DNNs的雷達波形設計

2.1 訓練與測試過程

使用DNNs設計雷達波形，即利用DNNs高效學習能力，對環境信息與該環境下經MI準則和SNR準則生成的最優波形之間非線性映射關系進行學習，調整DNNs自身權值參數，使DNNs權值兼具MI準則和SNR準則特性，避免建立聯合優化目標函數，達到聯合MI和SNR準則自適應生成最優波形的目的。由基于MI準則和SNR準則的波形設計過程可知，若已知環境中目標、雜波、噪聲、干擾等信息，可使用相關準則來設計最優波形。利用神經網絡進行波形設計，神經網絡生成信號的影響因素同樣為環境中目標、雜波、噪聲、干擾等4個因素。在實驗中，通常將噪聲設置為白噪聲，干擾的功率譜密度為高斯分布，故可將噪聲與干擾合并。綜上，神經網絡生成信號的影響因素為環境中目標、雜波、噪聲與干擾之和等3個因素。

本文方法分為訓練階段和測試階段，見圖3～4。

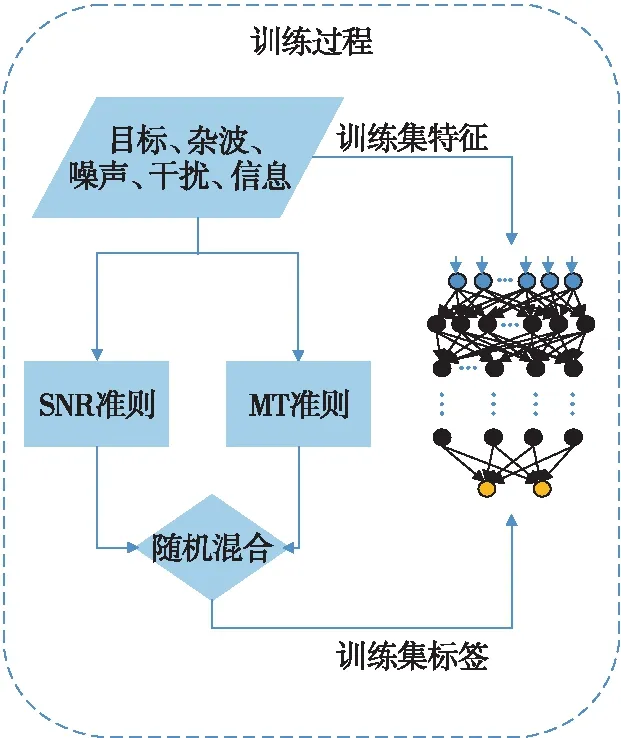
圖3 訓練流程圖

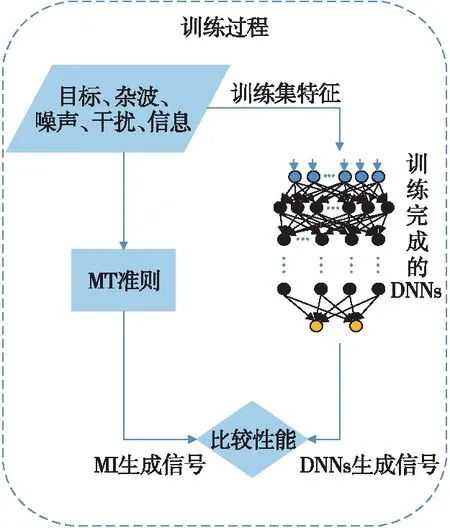
圖4 測試過程

圖3為訓練流程圖，該過程中，環境變量均為假設，首先對目標能量譜方差、雜波功率譜密度、噪聲與干擾之和的功率譜密度等3個變量進行假設取值，這3個變量的取值組成訓練集特征。然后根據MI準則和SNR準則來生成相應最優發射信號，將2種準則產生的波形進行混合并與其所對應的環境信息組成訓練集。之后使用訓練集對DNNs進行訓練，使得DNNs同時具有MI準則和SNR準則特性，達到2種準則融合的目的。該過程中，DNNs輸入層輸入為目標能量譜方差、雜波功率譜密度、噪聲與干擾之和的功率譜密度等3個變量的頻域采樣構成的序列，而輸出層希望得到的序列為不同準則生成波形的頻域采樣。

圖4為測試流程圖，經訓練階段得到訓練完成的DNNs，測試過程目的在于檢測本文方法有效性。為確保訓練集與測試集之間差異，測試過程中環境信息取值與訓練流程中不同。將同一組環境信息分別經由MI準則和訓練完成的DNNs來產生相應發射信號，將兩者生成信號分別作為雷達發射波形時，對比目標響應與回波之間的互信息量。該過程中，DNNs輸入層輸入為目標能量譜方差、雜波功率譜密度、噪聲與干擾之和的功率譜密度等3個變量的頻域采樣構成的序列，輸出層輸出為訓練完成的DNNs生成信號的頻域采樣序列。對比數據為MI準則產生的信號，并與線性調頻信號也進行了對比。

2.2 神經網絡參數設計

DNNs的層數以及各層神經元數量決定了其學習能力。一般來說，層數越多，每層神經元數量越多，網絡學習能力越強。但在實驗中，選取過多層數以及每層過多神經元數量會造成網絡的過擬合，導致其在訓練集上表現突出，而在測試集上表現不佳。故對網絡層數以及每層神經元的選擇至關重要，不可過多或過少。本文采用數據是在雜波響應、噪聲與干擾之和、目標響應、發射波形等4個變量頻譜上采樣500點得到的，其中前3個變量的1 500個采樣點作為DNNs輸入數據，發射波形的500個采樣點為網絡希望預測的數據。故本文神經網絡輸入層神經元數量為1 500，輸出層神經元數量為500。根據文獻[7]神經網絡設計經驗，本文設計的DNNs模型具有5層神經元，其中有3層隱藏層。每層所對應神經元數量分別為：1 500，3 000，1 500，750，500。輸入層1 500個神經元對應輸入的1 500點數據，而輸出層500個神經元對應輸出的500點數據。

激活函數為神經網絡提供處理非線性問題的能力，決定了網絡收斂速度與精度。常見激活函數有ReLU函數、sigmoid函數、LeakyReLU函數以及雙曲正切(tanh)函數。本文采用tanh函數，由于本文是回歸過程，故在網絡輸出層不使用激活函數。式(12)給出了tanh函數的數學表達式：

(12)

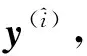
(13)

通過優化器將損失函數最小化，即把實際輸出與預測輸出之間的差距減小以提高預測精度。為提高運算速度，本文使用小批梯度下降法。其中學習率α=0.1，最小批數batch_size=100，迭代次數為10 000次。

3 實驗仿真

3.1 數據準備

3.2 實驗結果

將3.1節中生成的6 000組訓練數據送入DNNs進行訓練，之后將測試集1 000組數據送入訓練完成的DNNs得到神經網絡輸出，進而可得當發射信號為DNNs生成信號、MI準則生成信號和線性調頻信號時，雷達回波與目標之間的互信息量，見圖5。

從圖5可以看出，DNNs生成信號對應的互信息量要高于MI準則生成波形所對應的互信息量，且兩者要遠高于線性調頻信號所對應的互信息量。與僅基于MI準則產生的信號相比，采用本文方法生成的信號作為發射波形時，雷達回波與目標的互信息量最大提高了21.37 nat，與線性調頻信號相比提高了950.76 nat，由文獻[13]知，相應互信息量的提升降低了目標響應不確定性。

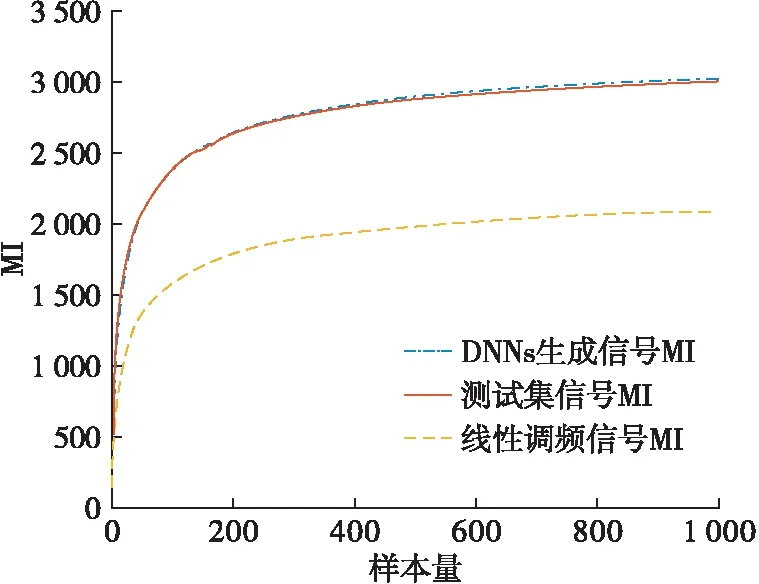
圖5 DNNs產生信號的MI對比圖

得到DNNs生成信號后，由式(3)可得接收機信號的SINR，經過10log(SINR)處理后，可得DNNs產生信號與MI準則生成信號以及線性調頻信號的SINR對比圖，見圖6。圖6中SINR曲線的分布規律與圖5中MI曲線大致相同，這是由SINR的表達式(3)與MI的表達式(4)之間的相似性來決定的，經過10log(SINR)處理，SINR的曲線趨于緊湊，使得SINR曲線與MI曲線大致趨勢相似。由圖6可知，采用本文方法生成的信號，相較于MI準則生成的信號所對應的SINR最大提高了1.35 dB，而相較于線性調頻信號最大提高了18.23 dB，由文獻[3]可知，信干噪比的提升提高了目標的檢測性能。

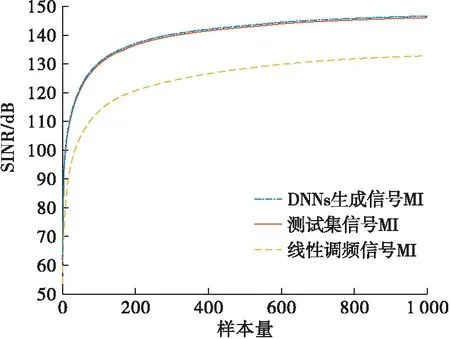
圖6 DNNs產生信號的SINR對比圖

由圖5和圖6可知，利用DNNs生成的信號無論是在MI還是SINR指標上都有所進步，這是因為DNNs綜合了MI和SNR 2種準則，結合了SNR準則分配更多能量在使SNR最大化的頻點上的特點與MI準則分配能量在利于信息提取頻點上的特點，優化發射波形能量分配，提高了雷達回波與目標之間的互信息量，降低了目標響應的不確定性，且提高了SINR指標，改善了雷達檢測性能。

4 結語

針對雷達波形設計多準則聯合優化問題，本文提出基于SNR準則與MI準則的DNNs的雷達波形設計方法。通過DNNs學習數據內在規律的能力，將SNR準則與MI準則分別產生的數據聯合起來訓練DNNs模型，使得DNNs模型兼顧SNR準則與MI準則的特征，且實驗結果表明，相較于MI準則，采用本文方法產生的信號與目標響應之間的互信息量與接收信號的信干噪比更高，降低了目標響應的不確定性，提高了雷達的檢測性能，為雷達波形設計提供了一個新思路。