基于動態布放的潛標錨系浮力配置優化研究

米智楠 ，程 堃 ，楊群慧 ，吳正偉 ，金 璐 ，唐 松

（1.同濟大學 機械與能源工程學院，上海 201804；2.同濟大學 海洋地質國家重點實驗室，上海 200092；3.同濟大學 國家海底科學觀測系統項目辦公室，上海 200092）

海洋潛標錨系是對海洋水下環境進行長期、定點、多參數剖面觀測的儀器設備系統[1]，具有全天候、長期無人值守、原位觀測的特點，能夠在惡劣的海洋環境條件下自動地對水體內部情況進行多參數剖面綜合監測，為其他海洋觀測手段所無法替代。國內外潛標錨系多采用單點繃緊系留方式，通過浮力保證錨系（尤其是掛載的儀器設備）的空間位置相對固定[2]。目前，對于潛標錨系的研究主要集中在錨系靜態和動態力學問題、計算方法驗證與實用軟件編寫，以及運用仿真軟件進行錨系動態過程分析等方面。Chee Meng Low等[3]采用雙速率時間步長方法建立了系留索動態方程；Sebastiao等[4]運用歐拉-拉格朗日方程構建系留索動態模型；Gobat等[5-6]在麻省理工學院（MIT）與伍茲霍爾海洋研究所（WHOI）的合作研究項目中，詳細分析了伍茲霍爾海洋研究所設計的多種海洋錨系姿態計算問題，并編寫了一套應用于實際工程的錨系姿態計算軟件；Baddour等[7]對拖纜布放/回收動力學進行了研究；Ablow等[8]最早運用數值仿真方法分析海纜動力學特性；王明午等[9]建立錨系數學模型，求解了靜態姿態問題；葛德宏等[10]基于集中質量法，通過MATLAB程序解算深海潛標在海流作用下的姿態；操盛文等[11]研究了一種潛標平臺受到不同參數海流作用下的姿態穩定性問題；劉愉強等[12]詳細分析了水動力學阻力系數，開發了對應的潛標錨系靜態姿態計算軟件；丁晶磊等[13]使用OrcaFlex仿真軟件對單點錨泊系統進行了水動力學建模與仿真；Wang Fei等[14]對拖纜在布放/回收期間的動態響應問題進行了研究，開發了一套數值仿真程序。

國內外研究人員做了很多有意義的工作，但目前只有較少的工作考慮了實際錨系裝置布放過程中的動態分析，更少有研究著重于分析浮力配置這一關鍵設計問題對于動態布放過程的影響，而布放過程是錨系經受的惡劣工況之一，系留索上的張力變化極大。因此，本文以對錨系動態布放過程的解算為基礎，研究浮力配置方案對潛標錨系的實際影響，進而為潛標錨系的浮力設計優化提供一定參考依據。

1 水動力學分析與建模

1.1 錨系模型與坐標系說明

文中所研究的潛標錨系基本構成為：浮球、傳感器儀器包、多段系留索、海床基（包括聲學釋放器）等，如圖1所示。不同顏色節點代表不同的組成部件：黑色代表海床基節點，黃色代表浮球裝置節點，藍色代表傳感器儀器包裝置節點。布放采用浮球和儀器包先行投放的方案，即標錨法。作業船只以較低的恒定速度頂流航行，首先將浮球、系留索和傳感器儀器包依次放入水中，浮球和傳感器儀器包入水后在船尾順列排布；當系留索基本拉成一條直線，且作業船只行駛到預定位置后，將海床基投放入水。圖1中，布放初始時刻錨系為平放在海面狀態，經過下沉過程之后在水平海流和浮力的作用下呈現傾斜豎立的狀態。

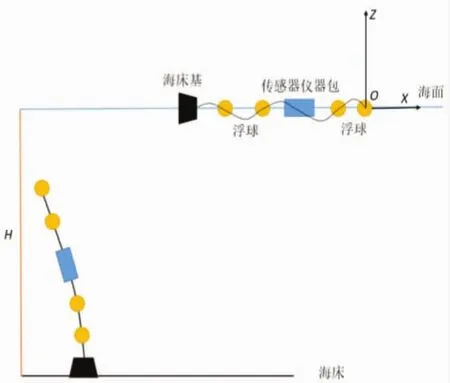
圖1 錨系與坐標系示意圖

潛標錨系工作水深為水下100 m，海流以平面線性流為主，采用二維坐標系進行分析和計算，所采用的流速廓線如圖2所示。計算所采用的坐標系以海平面水平線為X軸，豎直方向為Z軸。原點設在頂部浮球的型心，即每個錨系模型第一個下水節點的初始坐標均為（0,0）。在水中所有節點的Z軸坐標都為負值。海流方向與X軸正向相反。

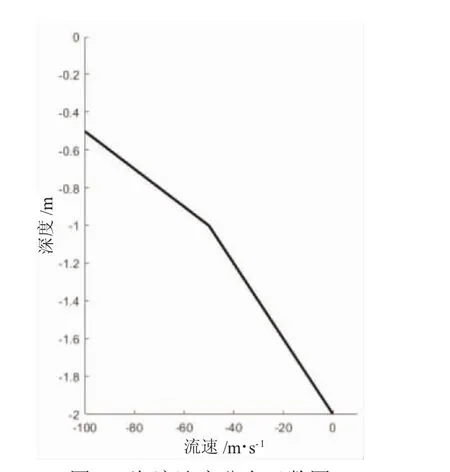
圖2 海流速度分布函數圖

1.2 力學分析

根據集中質量法，將系留索簡化為多段忽略彎曲剛度的彈簧，系留索自身及儀器裝置的質量、截面積等參數集中在系留索兩端的節點，受力分析如圖3所示。

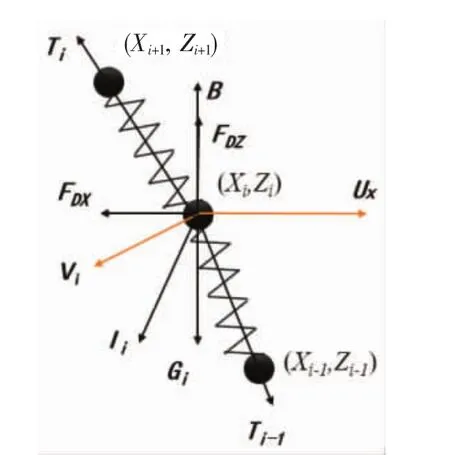
圖3 節點受力分析圖

在布放過程中，節點（Xi，Zi）受到的作用力包括：浮力B，重力G，系留索張力T，水動力阻力FD和慣性力I。圖中，UX為海流水平流速，V為該節點的運動速度。下標i表示第i個節點。

重力、慣性力和浮力的計算分別遵循牛頓第二運動定律和阿基米德定理。

1.2.1 張力計算 系留索上張力計算遵循胡克定律，如圖4所示。

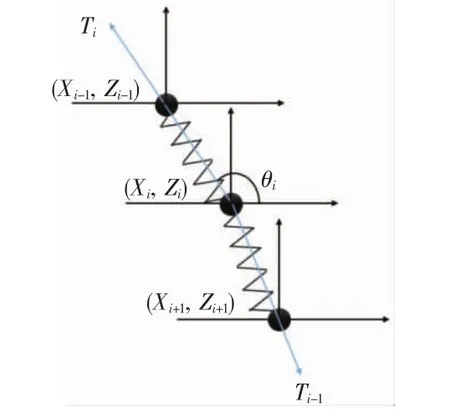
圖4 張力計算示意圖

式中：Ki為彈性系數；ΔLi為第i段系留索變化長度；Li為第i段系留索原長；Ei為彈性模量；Ai為系留索截面積。

節點i所受張力為上下緊鄰兩繩段的繩上張力之和:

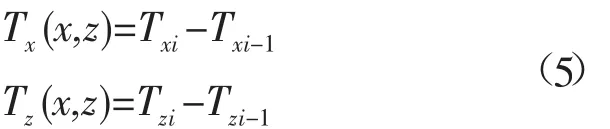
1.2.2 水動力阻力計算 水動力阻力計算方法遵循莫里森方程：

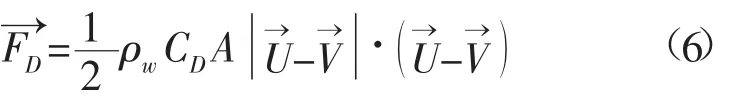
式中：ρw為流體密度；CD為流體綜合阻力系數；Ai為與海流作用方向垂直的有效面積；Ui為節點i處海流速度向量；Vi為節點i的速度向量。計算中將海流假設為理想的水平流，只有水平速度。

1.2.3 海底邊界條件 假定海底為泥沙地質。布放過程中，錨系的海床基在觸及海床時會與之發生碰撞及摩擦，并最終會陷入海床一定深度。將泥沙質海床簡化為彈簧阻尼系統模型[15]。其對節點產生的支持力FB和摩擦力fB邊界條件如下：

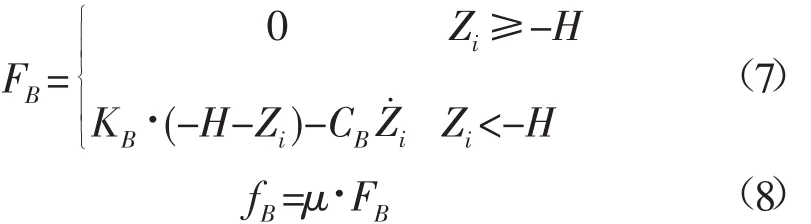
式中:KB為海床彈性系數；CB為海床阻尼系數；μ為海床摩擦力系數；H為海水深度。

1.2.4 運動控制微分方程 根據上述力學分析寫出對于節點i的運動控制微分方程:

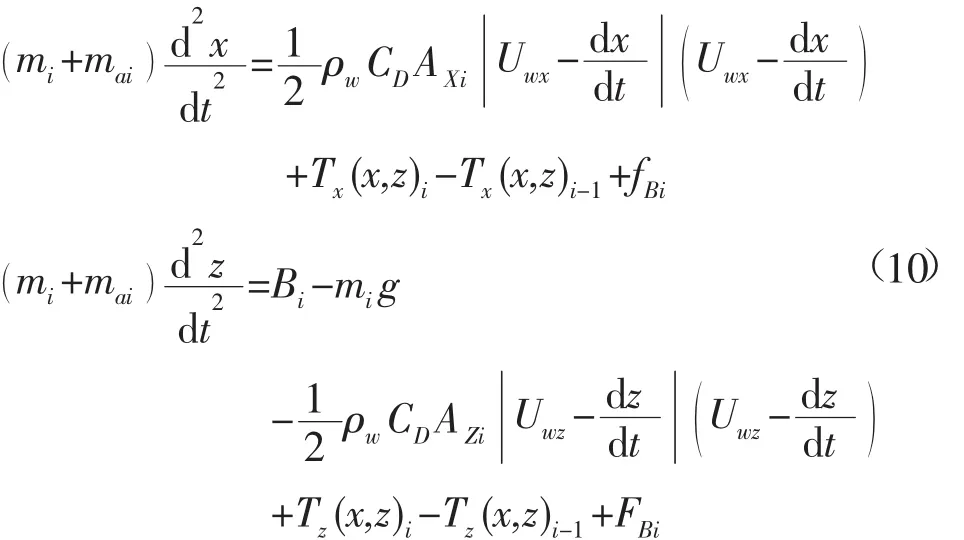
使用龍格-庫塔數值方法在時間域上解算上述微分方程組，即可求得運動過程中錨系節點的位移、速度等參數。

2 不同浮力配置的結構方案

潛標錨系通過多個浮球提供浮力，所設計錨系共需28個某型號浮球提供浮力。可采用4種浮力配置的結構方案：

（1）方案1：浮球依次串聯布置在整個潛標錨系的頂部。

（2）方案2：全部浮球均分為兩組，一組依次串聯置于潛標錨系頂部，即儀器包裝置上方，另一組浮球依次串聯安裝在海床基上方、儀器包下方，以提高海床基回收的成功率。

（3）方案3：全部浮球均分為7組（28個浮球每4個一組，共7個緊湊浮球組），每組為一整體（通過捆綁固定等方式），依次串聯布置在整個錨系頂部。

（4）方案4：全部浮球均分為7組，每組為一整體（通過捆綁固定等方式），其中4組置于潛標錨系頂部，即儀器包裝置上方，另外3組布置在儀器包裝置下方，即海床基上方，確保海床基的成功回收。

4種浮力配置方案的結構示意圖依次如圖5（a）～（d）所示。

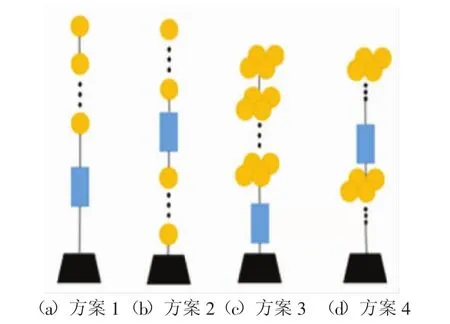
圖5 浮力配置結構方案示意圖

3 動態布放過程仿真與分析

3.1 節點劃分

以圖5中方案3的計算模型初始信息作為示例。如圖6所示，將整個潛標錨系分為14個節點，1號節點為海床基節點，2～6號節點為系留索節點，7號節點為儀器包裝置節點，8～14號節點為浮球節點。每相鄰兩個節點之間由一個系留索段連接,整個系統按照圖6順序排列共有13個纜段,后續計算將研究節點的運動參數信息和系留索段上的張力分布。

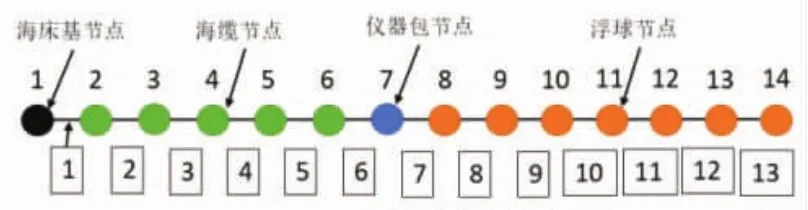
圖6 方案3計算用節點劃分方案

3.2 仿真參數說明

數值計算中所使用的各項力學公式系數、系留索材料參數、結構節點質量信息參數分別如表1～表3所示。

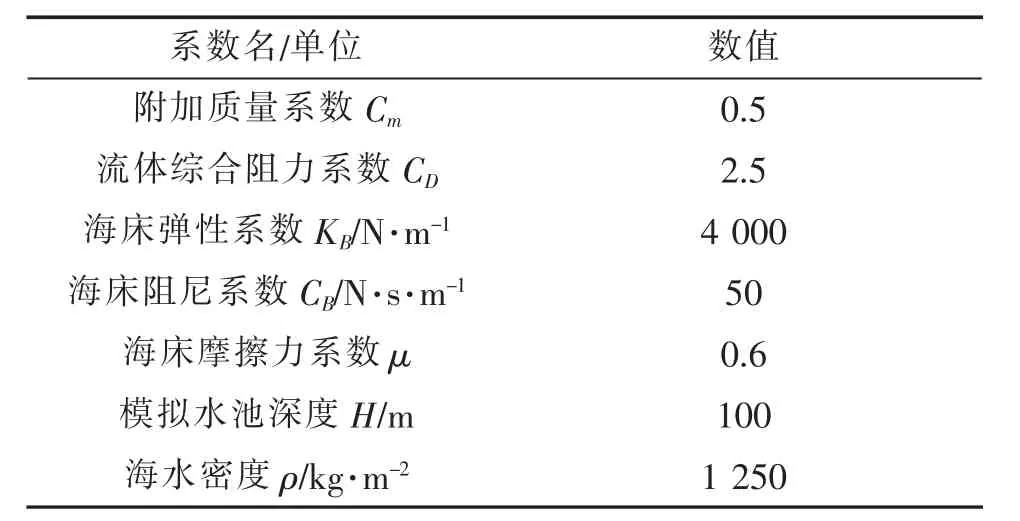
表1 各項水動力學系數

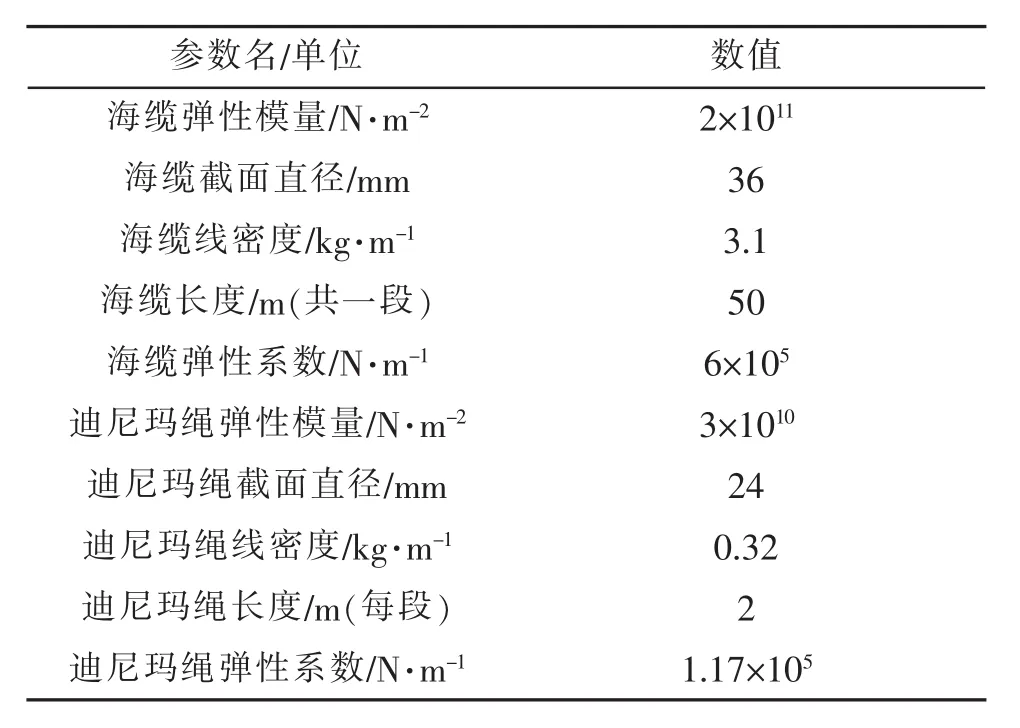
表2 系留索材料參數

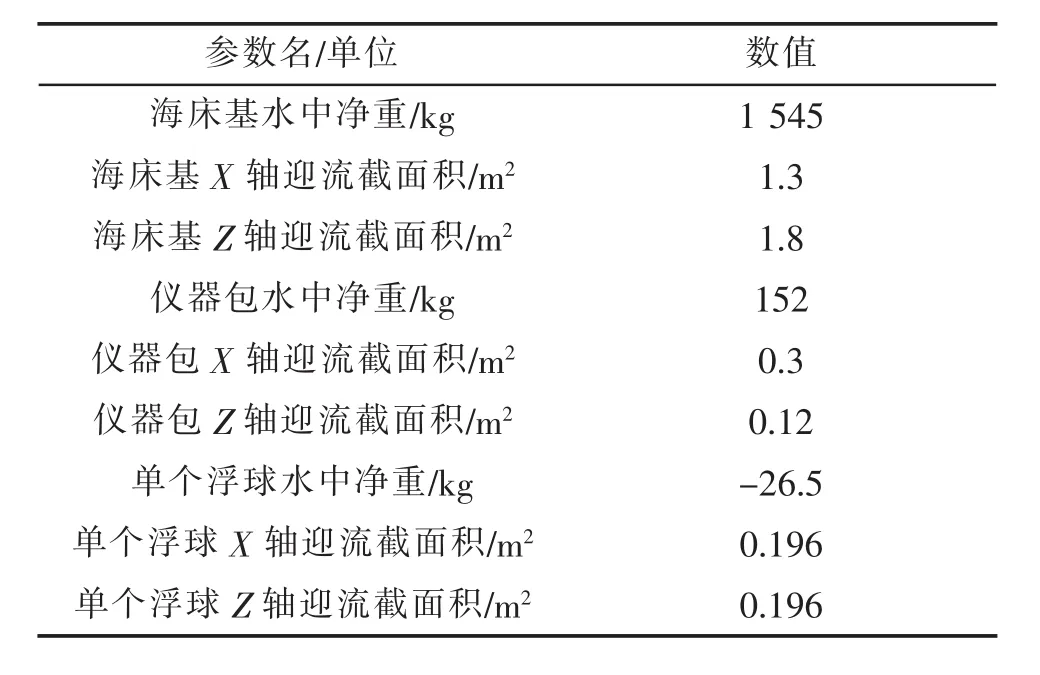
表3 各結構節點參數

3.3 姿態變化

數值計算程序模擬了從潛標錨系水平放置于海平面開始，一直到海床基著底的完整過程。經過多次計算，確定模擬時長約為80 s（方案1錨系的模擬運動難以達到穩定態，設置模擬計算時長為150 s）。通過對4種方案的垂直和水平兩方向位移、運動軌跡圖像進行分析和比較，以探究4種方案的各自特性。

以方案3錨系的姿態變化圖說明錨系布放過程的姿態變化情況。將整個布放過程時間等分為10段，在11個時刻點上考察錨系節點位置，將各時刻點上全部錨系節點的位置連線得圖7，直觀表現了方案3所示錨系姿態在布放過程中的變化情況。入水時刻錨系處于水平漂浮姿態；0～16 s區間，浮球節點保持漂浮狀態，海床基和儀器包節點之間的錨系逐漸下沉，本文稱為布放初始階段；24～56 s區間，整個錨系水平方向上收攏，保持近似豎直狀態下沉，稱為聚攏下沉階段；64～80 s區間，海床基沉底，錨系海床基以上節點在海流的作用下漂移至穩定位置，錨系最終呈現傾斜狀態，稱為著底穩定階段。

圖7 方案3潛標錨系水中姿態變化示意圖

3.4 垂向運動和著底過程分析

4種浮力配置方案在垂向運動和著底的仿真分析如圖 8（a）～（d）依次所示。

以圖8（c）為例，14條線代表14個節點的垂向位移規律。

錨系節點垂向運動規律與圖7中的姿態變化過程一致。整個錨系布放過程大致經歷0～16 s的布放初始階段，浮球節點幾乎不發生垂直方向位移，海床基、儀器包和EM纜逐漸下沉；16～56 s的聚攏下沉階段，整個錨系同步下沉；56～80 s的著底穩定階段，海床基錨定，其余各節點逐漸達到穩定態。

垂向運動分析主要對比考察海床基沉降深度和著底時間。沉降深度過大會導致海床基無法回收，影響海床基正常工作；著底所需時間越長，錨系布放安全性越低。

沉降深度方面，4種方案海床基的沉降深度幾乎相同，沒有明顯差別。著底時間方面，方案1錨系下沉速度最快，最早著底，但海床基沒有穩定，而是緩慢地被逐漸拉起，分析可知是由于大量浮球分散在淺層海流快速區域，受到海流拖曳力過大使得錨系無法錨定；方案3和方案4的著底時間較方案1和方案2更遲，分析可知是由于錨系結構緊湊，錨系更早進入到聚攏階段，受到浮球浮力作用的時間更長。

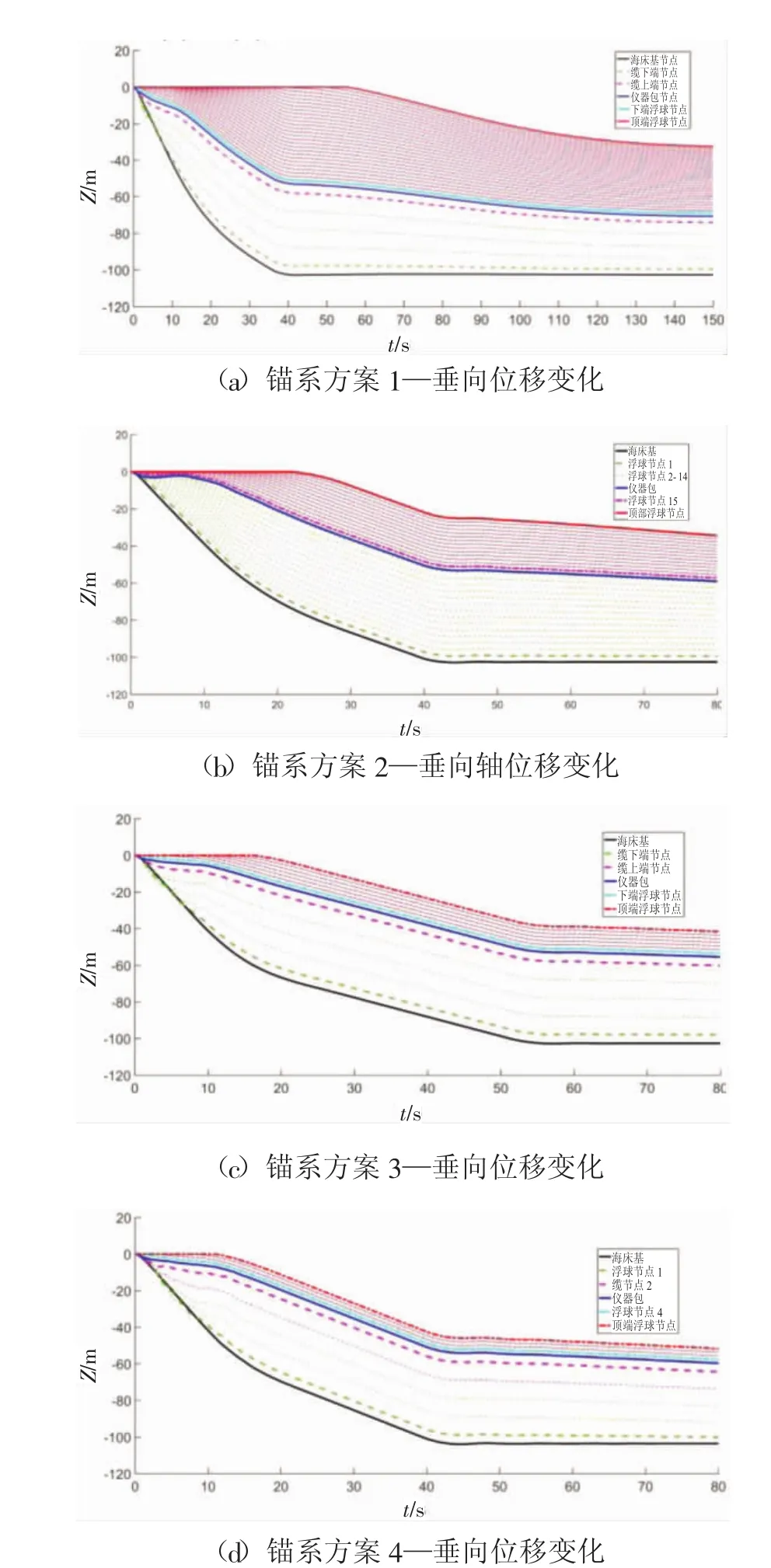
圖8 垂直方向位移圖對比

3.5 水平運動分析

4種方案的潛標錨系在水平方向的運動狀態如圖 9（a）～（d）所示。

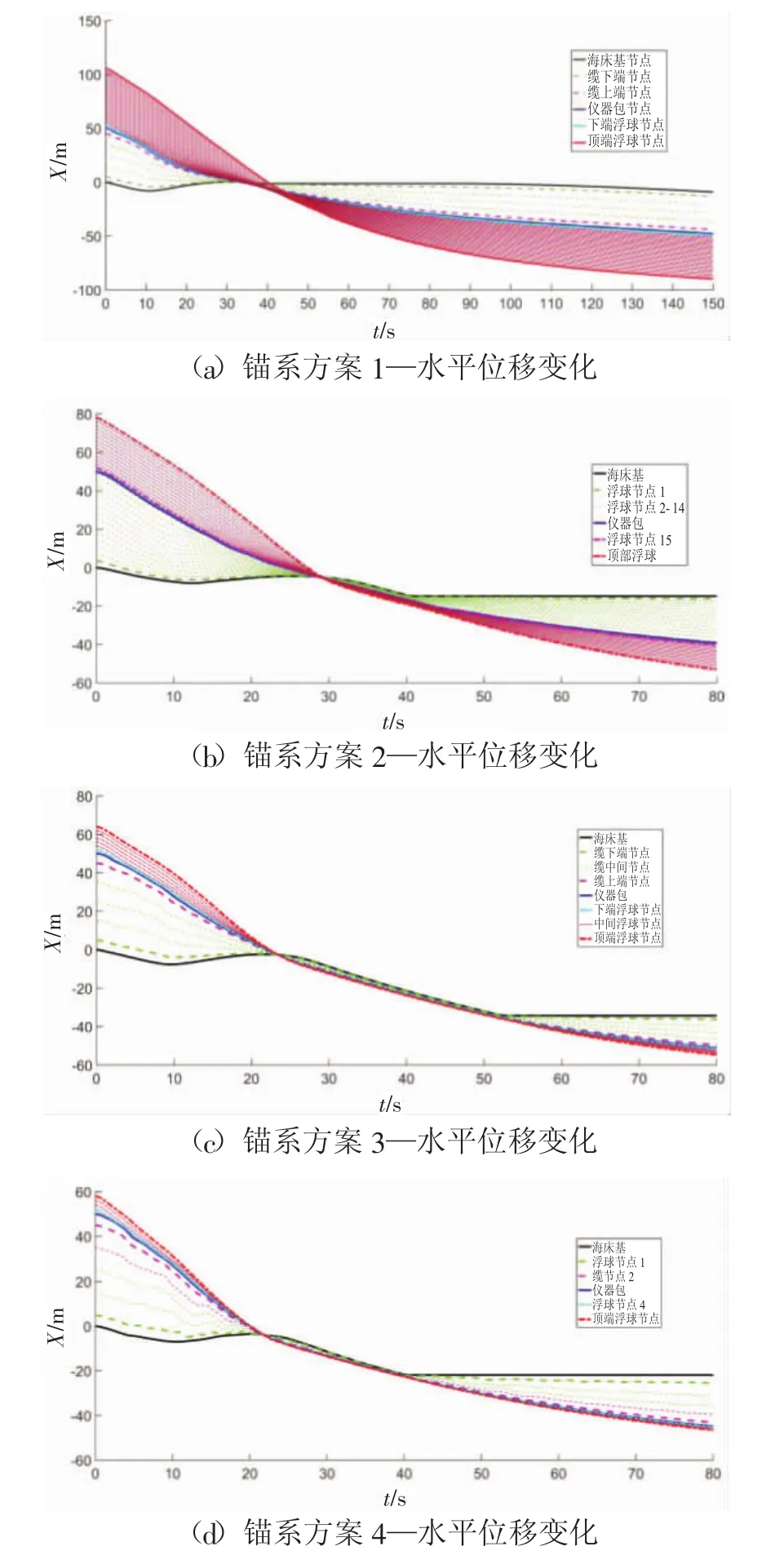
圖9 水平方向位移圖對比

以圖9（c）為例，14條線代表14個節點的水平位移規律。整個錨系經歷以下過程：0～16 s區間的布放初始階段；16～56 s區間的聚攏漂移階段，整個錨系被海流拖曳向X軸負方向偏移；56～80 s的著底穩定階段，海床基錨定在海底，不再發生水平位移。

水平運動分析主要對比考察錨系海床基水平偏移距離，偏移距離越大，越難被定位回收，可能造成工程損失。

圖9（a）表明方案1始終未能達到穩定平衡狀態，海床基在著底后仍然被錨系緩慢拖動，產生位移。分析可知，大量浮球分布在淺層海流速度較快的區域，受到的海流拖曳力較大，導致海床基無法錨定。其余3種方案中，方案2的錨系漂移距離最小，方案3和方案4的漂移距離近似，均大于方案2。分析可知，方案3和方案4的錨系節點少而緊湊，更快進入到聚攏漂移階段，導致更大的漂移距離。推斷隨著水深的增加，方案3和方案4的漂移距離將與方案2接近。

綜合分析錨系節點水平位移與垂直位移的規律，可得到如下結論：錨系長度方向上設計越緊湊，則海床基在布放后越早受到浮力節點的作用，這會使整個錨系著底時間變長，漂移距離變大。若要改善這一性能指標，應適當加長上部浮球節點與下部儀器設備連接系留索的長度，使海床基等結構在布放初期能快速原位下沉。

3.6 布放過程運動軌跡分析

圖10為4種錨系方案在布放中的運動軌跡。如圖所示，4種錨系方案運動趨勢近似，只在趨于穩態的階段呈現出靜態姿態的差別。方案1和方案2整個錨系長度更長，占據的水域也更大。方案3和方案4結構緊湊，系留索段與豎直方向夾角更小，從而可以保證傳感器等設備的傾角較小，因此，方案3和方案4更能滿足其對工作姿態的要求。綜合可得如下結論：減少上部浮球的數量和浮力總量配置以及減小錨系長度，有利于錨系保持姿態垂直度。

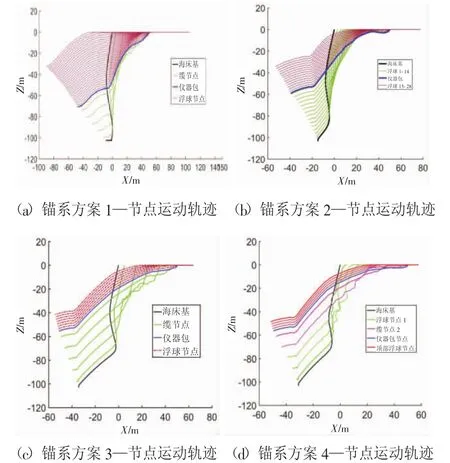
圖10 錨系運動軌跡圖對比

3.7 張力分布變化分析

圖11 為4種浮力配置結構方案在布放過程中的張力變化圖。布放過程中，系留索承受交變應力。

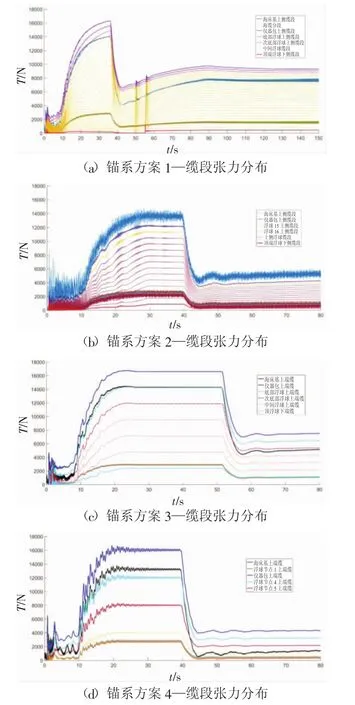
圖11 纜段張力分布圖對比

方案1和方案3的最大張力出現在儀器包上側連接浮球節點的纜段上，而方案2和方案4的最大張力出現在海床基上側的纜段上。根據系統結構設計方案，方案2和方案4的海床基節點與方案1和3的儀器包節點都是浮力和重力性質分界節點。由此推斷，錨系中系留索最危險的部分出現在浮力節點與非浮力節點的連接段上。

在最大張力值方面，方案2和方案4的最大張力值約為1.4×104N，方案1和方案3的最大張力值約為1.6×104N。在穩態張力值方面，方案2和方案4中緊鄰海床基的上側纜段的穩態張力值約為5 000 N；方案1和方案3中緊靠儀器包的上側纜段穩態張力值約為7 000 N。這說明，浮球分散布置（即儀器包和海床基之間布置浮球）的結構方案有助于減少纜上載荷。作為強度參考，本文研究的錨系對象采用的系留索材料為迪尼瑪繩和鎧裝海纜，這兩種材料的抗拉強度都超過了50 kN。

在纜段張力的波動振蕩方面，方案1和方案3的纜段張力值振蕩幅值較小，方案2和方案4的纜段張力值震蕩幅值更大。這說明浮球分散布置的結構設計會導致纜段張力的震蕩程度加劇。

系留索上張力值的最大值均出現在海床基著底的瞬間，海床基著底這一行為會帶來劇烈的系留索張力變化。圖11中方案1、方案2、方案3的著底張力變化值約為9 kN，方案4的著底張力變化值約為10 kN。

綜合分析張力變化分布圖，可得到如下結論：采用緊湊浮球組設計的錨系纜索動態張力指標更優；采用纜索上下部分散布置浮球方案的錨系纜索穩態張力值指標更優。設計時應根據纜索的實際工況要求，選擇合適的浮力配置方案。

4 結論

通過對錨系動態布放過程中運動姿態軌跡、垂向運動、水平運動、著底時間、全程張力變化等關鍵項目的仿真，對比分析了4種浮力配置結構方案的力學性能指標區別和原因，提出了如下改進思路：

（1）方案3和方案4所采用的緊湊浮球組的設計方式有效縮短了錨系長度，改善了錨系的姿態垂直度，但在著底時間和水平漂移指標上表現較差。為了改善這兩個指標，可在減少上部浮球節點數量（用大浮球替代多個小浮球）和浮力總量的基礎上，適當加長上部浮球節點與下部非浮力節點之間的距離。

（2）浮力節點分散布置（即儀器包和海床基之間布置浮球）的方式可以有效減少纜索上的張力極值，但是會導致更大的張力變化幅度。在本研究中，由于纜段張力極值遠遠低于所用系留索的抗拉強度，因此方案3的設計在穩態張力值和動態張力變化方面具有較好的綜合性能，能有效改善纜索的受力情況。

（3）采用以下4種錨系浮力配置方案，可有助于改善錨系布放動態性能：①減少浮力節點數量；②適當加長上部浮力節點與下部非浮力節點之間的距離；③浮力節點分散分布；④適量減少上部的浮力節點。