基于雙變異策略差分進化算法的模糊PI參數整定

陳春霞，孫祥娥

(長江大學電子信息學院，湖北 荊州,434024)

模糊PID控制器因融合了模糊控制優良的動態性能和PID控制器良好的穩定性能而得到廣泛應用，根據所應用的系統不同，通常采用比例、積分、微分3個控制規律中的全部或部分構成3種不同的控制器，即模糊P+I+D控制器(FPID)、模糊P+I控制器(FPI)和模糊P+D控制器(FPD)。模糊PID控制器的性能與輸入量化因子、輸出比例因子、隸屬函數以及模糊控制規則等參數的選擇密切相關，而參數間的相互影響使模糊PID控制器的參數整定相比于傳統PID控制器更為復雜。到目前為止，也沒有特別好的適用于模糊PID參數整定的指導性方法。

隨著智能優化算法的發展，其在PID控制器參數整定領域的應用已成為一個研究熱點[1-5]。其中，差分進化(Differential Evolution，DE)算法因結構簡單、待定參數少，在求解非線性、不可微、多極值和高維復雜函數時表現出較強的全局收斂能力和魯棒性而受到青睞，并在PID參數優化整定中得到成功應用[6-8]。然而，差分進化算法仍然存在以下問題：進化后期的種群多樣性急劇下降，全局搜索能力被削弱，導致算法極易陷入局部最優而早熟收斂[9]。為此，研究者提出了一系列針對變異策略、變異因子和交叉因子的改進差分進化算法[10-12]，提高了算法的應用性能。

本文提出一種基于雙變異策略協同工作的自適應差分進化算法(簡稱為DSDE)。該算法將經典差分進化算法中的DE/target-to-best/1和DE/rand/2兩種變異策略各自生成的變異個體通過一個標量權重因子組合成新的個體，并采用隨當前迭代次數變化的正弦函數來動態調整該權重因子，同時采用Z型函數根據當前迭代次數動態調整變異因子，使得算法在“開發”和“探索”之間達到一個良好的平衡，在一定程度上提高算法的收斂速度和搜索精度。然后，將該算法應用于模糊PI控制器的參數整定，并通過仿真實驗來驗證其優越性。

1 差分進化算法

差分進化算法是一種基于群體差異的智能優化算法，其包括初始化、變異、交叉和選擇4個基本步驟。

(1)初始化。根據式(1)在解空間隨機產生一個初始種群：

(1)

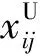
(2)變異操作。在初始種群中隨機選擇若干與當前個體xi(t)互不相同的個體xp1(t)、xp2(t)、xp3(t)、…，根據不同策略進行變異操作，生成新的個體hi(t+1)。差分進化算法常用的5種變異策略如下：

①DE/rand/1：

hi(t+1)=xp1(t)+F(xp2(t)-xp3(t))

(2)

②DE/best/1：

hi(t+1)=xbest(t)+F(xp1(t)-xp2(t))

(3)

③DE/target-to-best/1：

hi(t+1)=xi(t)+F(xbest(t)-xi(t))+

F(xp1(t)-xp2(t))

(4)

④DE/best/2：

hi(t+1)=xbest(t)+F(xp1(t)-xp2(t))+

F(xp3(t)-xp4(t))

(5)

⑤DE/rand/2：

hi(t+1)=xp1(t)+F(xp2(t)-xp3(t))+

F(xp4(t)-xp5(t))

(6)

式(2)～式(6)中：t為當前迭代次數；xbest(t)為當前最優個體；F為變異因子。

(3)交叉操作。根據式(7)將hi(t+1)和xi(t)按照一定的交叉概率進行交叉操作，產生試驗個體vi(t+1)：

(7)

式中：下標j代表個體向量的第j維分量；CR為交叉概率因子。

(4)選擇操作。按式(8)將試驗個體與目標個體基于適應度函數進行比較，確定進入下一代的個體：

xi(t+1)=

(8)

式中：f(·)為適應度函數。

按以上步驟進行迭代，直至最大進化代數或滿足其他停止進化條件。

2 雙變異策略差分進化算法DSDE

2.1 雙變異策略

大多數基于群體的搜索算法都試圖在算法的全局探索能力和局部開發能力之間取得平衡[13]。對于差分進化算法而言，一種有效的方法是通過選擇合理的變異策略來實現。

在差分進化算法的5種變異策略中，DE/target-to-best/1策略因所有個體在進化過程中都朝著適應度值最好的個體進化，使得算法更快地收斂于最優值，有利于提高算法的局部開發能力；而DE/rand/2策略因基礎向量的隨機性以及采用兩個向量差進行變異，增強了算法的全局探索能力。

有別于傳統DE算法通常選取一種策略進行變異操作，本文采用雙變異策略協同工作，在進化過程中使用DE/rand/2和DE/target-to-best/1兩種變異策略各產生一個變異向量，并采用基于當前迭代次數的正弦函數動態調整加權因子ω，將兩個向量線性組合成最終的變異個體向量。具體計算過程如式(9)～式(12)所示：

F(xp4(t)-xp5(t))

(9)

F(xp1(t)-xp2(t))

(10)

(11)

(12)

式(11)中：tmax為最大進化代數。

2.2 變異因子F

變異因子F是差分進化算法的重要參數，它控制著種群的多樣性和收斂性。進化過程中，F值較小時，群體的多樣性減小，算法極易陷入局部極值而過早收斂；F值較大時，群體的多樣性增加，算法雖然容易跳出局部極值，但收斂速度會減慢。標準差分進化算法中F一般在[0,2]區間取一個固定值，這種取值方法不能充分發揮變異因子在不同進化階段的作用。為此，本文采用隨迭代次數的增加而減小的Z型函數對變異因子F進行動態調整，計算公式如下：

(13)

F(t)=Fmin+α(t)(Fmax-Fmin)

(14)

式中：Fmax和Fmin分別為變異因子的上限和下限。

結合式(9)～式(12)可知，在進化初期，種群多樣性較高，F取較大值有利于種群朝著最優解進化的同時還能保持其多樣性；在進化后期，算法逐漸收斂，F取較小值有利于在最佳區域周圍進行搜索的同時適當提高種群多樣性，從而提高算法的收斂速度和搜索精度。

DSDE算法的具體流程如圖1所示。

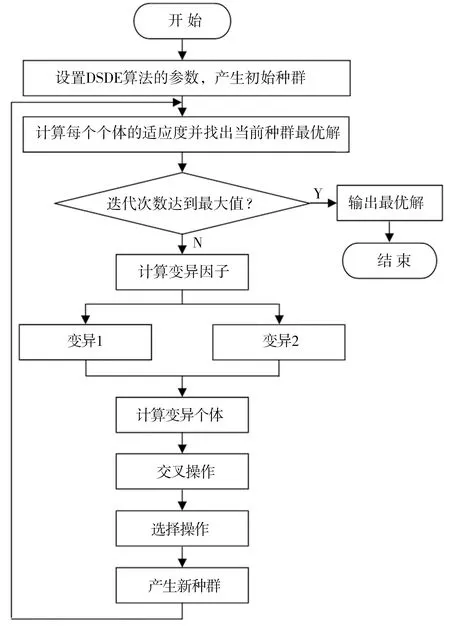
圖1 DSDE算法流程

3 基于DSDE的模糊PI參數整定

如圖2所示，本文研究的模糊調諧PI控制器由模糊控制器和PI控制器組成。模糊控制器首先將偏差e、偏差變化ec通過量化因子Ke和Kec變換成模糊量E和EC，然后根據模糊規則對模糊輸入量進行模糊推理得到模糊控制量，最后乘以相應的比例因子，輸出到PI控制器，對其比例系數和積分系數進行在線修改。

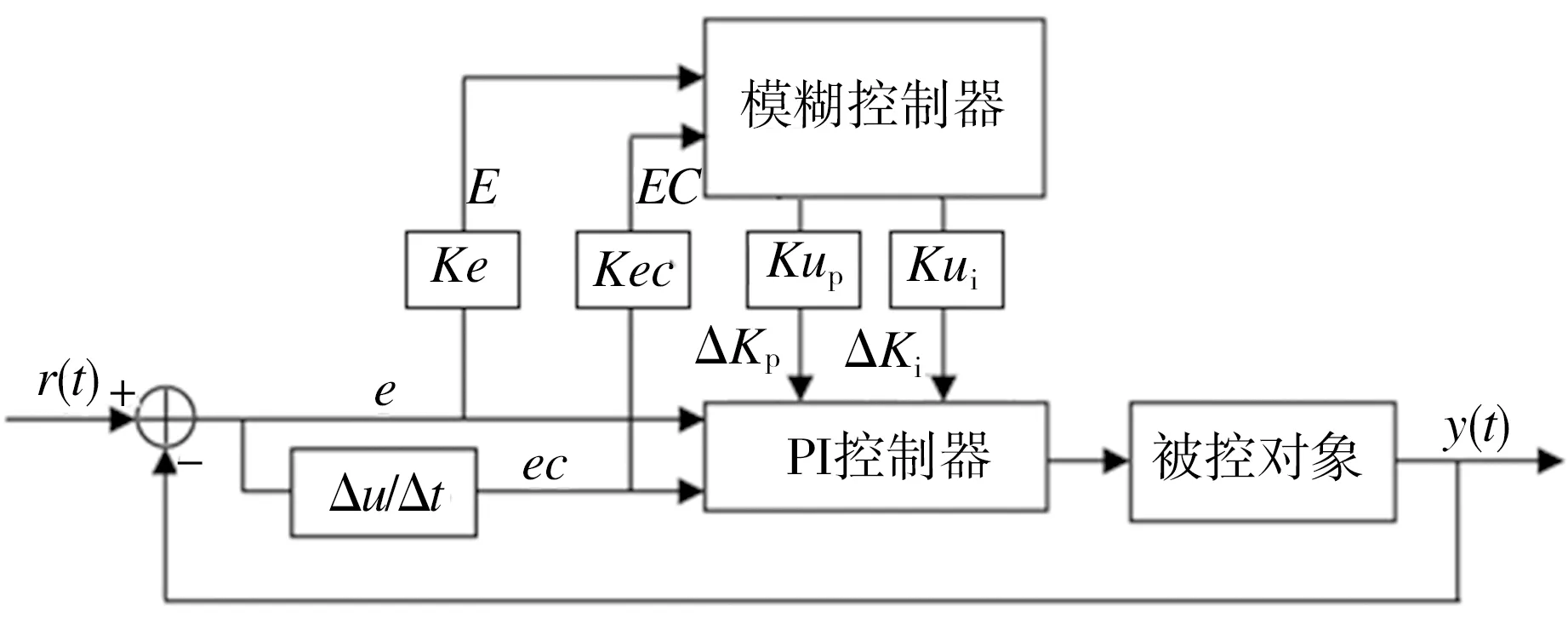
圖2 模糊PI控制器結構

然而，模糊調諧PI控制器的控制效果很大程度上取決于輸入量化因子、輸出比例因子、隸屬函數和模糊規則的選擇，其中輸入量化因子和輸出比例因子是影響全局的參數。為此，本文通過DSDE算法對模糊PI控制器參數進行整定優化，將Ke、Kec、Kup、Kui這4個參數構成一個4維向量，進行浮點數編碼，組成差分進化算法的個體向量。以常用的系統性能指標函數ITAE(時間乘絕對偏差積分)作為DSDE算法的適應度函數。

4 仿真實驗

在MATLAB環境下，采用某二階系統作為仿真對象，其傳遞函數如下：

(15)

首先設定DSDE參數：種群規模通常為問題空間維度的5～10倍，種群數越大，種群多樣性越豐富，獲得最優解概率越大，但是計算時間更長，本文問題空間維度為4，為節省計算量，取種群數為維度的5倍，即NP=20；變異因子下限Fmin=0.1、上限Fmax=2；交叉概率因子CR=0.6；最大迭代次數tmax=50；個體各個維度分量的尋優范圍均設為[0.001,2]。仿真開始時給系統施加一個階躍輸入信號，采樣時間ts=0.001 s，仿真時長為1 s。

經過DSDE算法針對上述系統進行FPI控制器的參數整定優化，得到最優控制器參數為Ke=1.03、Kec=0.001、Kup=1.897、Kui=0.05，控制系統性能指標ITAE值為3.667。

圖3為DSDE算法優化得到的性能指標ITAE變化曲線。由圖3可以看出，ITAE值在進化過程中不斷減小，DSDE算法收斂速度較快，且在進化后期仍然具有較強的探索能力，在第44步時收斂到最優值。

為了驗證DSDE算法在FPI參數整定中的優越性，將本文DSDE-FPI與傳統FPI、采用標準差分進化算法進行參數整定的DE-FPI以及基于文獻[8]中自適應變異PID參數整定的AMDE-FPI進行仿真對比分析，得到二階系統(式(15))的階躍響應曲線如圖4所示，部分性能指標(調節時間ts、峰值時間tp、超調量δ)如表1所示。

圖3 ITAE指標變化曲線

圖4 系統階躍響應曲線

Table 1 Comparison of performance indexes of different control methods

控制方法ts/stp/sδ/%FPI0.2650.2286.16DE-FPI0.0690.1401.13AMDE-FPI0.0930.2200.57DSDE-FPI0.0640.1390.69

由表1可知：從這3項指標來看，DSDE-FPI均優于FPI和DE-FPI，并且DSDE-FPI的超調量比DE-FPI的超調量降低了38.9%；與AMDE-FPI相比，雖然DSDE-FPI的超調量大了0.12個百分點，但調節時間和峰值時間分別減少了31.2%和36.8%。綜合來看，與FPI、DE-FPI及AMDE-FPI控制相比較，DSDE-FPI控制具有比較明顯的優勢。

5 結語

本文提出了一種基于雙變異策略協同工作的差分進化算法DSDE。該算法選用有助于提升局部開發能力的DE/target-to-best/1變異策略以及有助于提升全局探索能力的DE/rand/2變異策略，在進化過程中同時生成兩個變異個體，并采用隨進化代數變化的權重因子ω將兩個變異個體線性組合成一個新的個體，同時還采用隨進化代數變化的Z型函數對變異因子F進行動態調節。在進化初期種群多樣性較好的情況下，其朝著最優解進化的同時搜索范圍也得到有效擴大；在進化后期算法收斂的情況下，種群在最佳區域周圍進行搜索的同時也能適當提高多樣性。從本文算法在以某二階模型為被控對象的模糊PI參數整定中的應用效果來看，與FPI，DE-FPI、AMDE-FPI控制器相比，DSDE-FPI控制器在考慮超調量、調節時間和峰值時間3個主要指標的綜合性能上優勢明顯。