對于2020年北京市適應性考試圓錐曲線題的思考
2020-06-13 08:38:18楊雪芹鄭拴平
高中數(shù)理化 2020年2期
關鍵詞:探究
楊雪芹 鄭拴平
解析幾何是運用代數(shù)方法研究幾何問題或用幾何方法研究代數(shù)問題的一門學科.解析幾何知識與其他知識聯(lián)系緊密,綜合性強,是選拔人才的必考內(nèi)容,能重點考查學生知識儲備中的基礎性、通用性的知識.著名的數(shù)學教師孫維剛曾表示學數(shù)學應該“八方聯(lián)系,渾然一體,漫江碧透,魚翔淺底”. 這是一種體現(xiàn)數(shù)學美感的意境,更是彰顯學生能力的一個層面.本文對2020年北京市適應性考試圓錐曲線試題進行探究,供讀者參考.
1 問題呈現(xiàn)

(1)求橢圓C的方程;

2 解法探究

(2)證法1 (直線方程角度代數(shù)法)


圖1




證法2 (點的坐標角度代數(shù)法)

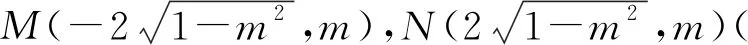
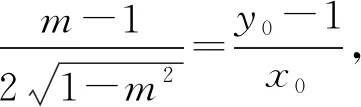



證法3 (參數(shù)方程角度換元法)




所以點D在x軸上.
證法4 (壓縮變形角度幾何法)
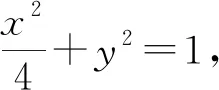
如圖2所示,設直線BD交圓O于點P,連接AM,AP. 在四邊形AMBP中,∠MBD=90°,∠AMB=∠APB=90°,所以四邊形AMBP是矩形,則BP=AM. 又因為AM=AN,所以BP=AN.
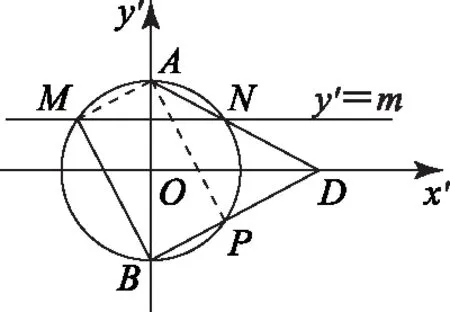
圖2
根據(jù)相交弦定理得DP·DB=DN·DA,即(DB-BP)·DB=(DA-AN)·DA.所以DB=DA,因此點D在線段AB的垂直平分線上,即點D在x′軸上.所以,在原坐標系下,點D在x軸上.

3 推廣與變式
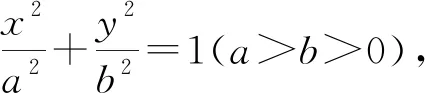
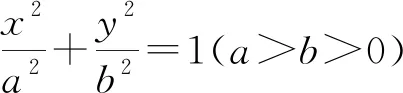
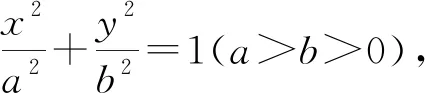



有興趣的讀者可對上述幾個變式進行推導,限于篇幅,此處不再贅述.
2020年是北京市新一輪高考改革的起始年,試題既要平穩(wěn)過渡,又要呈現(xiàn)出“一核四層四翼”的功能.從本文可以看出,試題設計明確、簡潔,解答角度靈活,有利于人才的選拔及教學方向的引導,能培養(yǎng)學生提出問題、分析問題、解決問題等能力.
猜你喜歡
中國交通信息化(2023年11期)2023-12-26 07:43:50
中學生數(shù)理化·高三版(2023年1期)2023-09-04 09:24:31
中學生數(shù)理化·七年級數(shù)學人教版(2022年5期)2022-06-05 07:51:48
中等數(shù)學(2021年11期)2021-02-12 05:11:46
今日農(nóng)業(yè)(2019年14期)2019-09-18 01:21:42
快樂語文(2018年13期)2018-06-11 01:18:16
中等數(shù)學(2018年11期)2018-02-16 07:47:42
中學生數(shù)理化·高一版(2017年5期)2017-06-07 07:09:32
中學數(shù)學雜志(初中版)(2016年4期)2016-10-08 09:21:22

