基于三角模糊熵-折衷排序法的終端區管制運行效率評估模型

閆少華，孫佳琦，張兆寧

(中國民航大學空中交通管理學院，天津 300300)

管制系統運行效率是管制單位最大限度的運用管制規則和系統資源，通過優化資源配置，使空中交通流處于快速、暢通、有序的程度，是反映管制系統運行狀態的重要指標[1]。終端區管制系統是民航管制系統的重要組成部分，該系統中，空域資源有限，航路航線結構復雜，飛行狀態復雜，這使得終端區成為空中交通運輸網絡的瓶頸。為了解決空域擁堵、航班延誤的問題，需要客觀科學地對終端區管制系統運行效率進行評估。

目前，中外學者已經逐步開展了空中交通管制系統運行效率的相關研究。在國外，美國交通運輸部和聯邦航空管理局，共同建立并完備了空中交通管制專家績效評價數據庫，為空中交通管理評價提供了有效工具[2]。EuroControl 2002在客觀數據的基礎上，從容量、效率、安全和環境影響四個方面評價空中交通管理系統的效率[3]。Viswanathan等[4]采用串聯設計進行仿真建模，同時考慮層次結構，從戰略、預戰術以及戰術三個層面研究管制運行效率。Bronsvoort等[5]提出了一種分階段飛行效率的評估方法，構建了空中交通管理(air traffic management，ATM)性能與飛行效率的評估關系框架。

在中國，羅貫中等[6]以效率的內涵作為出發點，基于系統工程理論，從人-機-環三方面建立空管運行效率指標體系。張兆寧等[7]建立了基于數據包絡分析(data envelopment analysis，DEA)的空域系統定量評估模型。杜實等[8]基于管制間隔運用現狀建立了管制運行效率評估指標體系，利用含約束錐的DEA模型進行了管制運行效率評估。王夢麗等[9]利用DEA法中的兩階段BCC模型，對機場管制系統運行效率進行評估。林碩等[10]引入管制運行效率性指標，利用灰色關聯逼近理想解法，對終端區管制系統運行質量進行定量評估。

綜上所述，現有的管制運行效率相關研究通常是針對整個管制系統，專門針對終端區管制系統運行效率的研究相對缺乏,并且常用的主觀賦權法多為基于1～9標度法的層次分析法，該方法構造一致性矩陣較困難，且所得出的結果與人的實際思維有較大差距。

首先根據終端區管制系統實際運行特點，構建適用于終端區管制系統運行效率評估的指標體系；其次選擇能夠更好反映專家真實判斷的三角模糊數法確定主觀權重，利用最小信息熵法將三角模糊數法求得的主觀權重和熵權法求得的客觀權重相結合，得到優化后的組合權重；最后運用折衷排序法(VIKOR)結合組合權重求出終端區管制系統運行效率評估值，并根據效率評估值進行排序，對終端區管制系統運行效率進行科學評價。

1 終端區管制系統運行效率評估指標體系建立

終端區管制系統是一個多元的輸入輸出系統，為其所轄空域的航空器提供空中交通管制服務。其基本運行過程為：根據現有的管制規則、終端區空域結構、天氣狀況以及航行情報等輸入信息，通過利用通信導航監視設備、進程單填寫來實施管制行為，輸出進離場管制服務。因此，終端區管制系統運行效率是可以用管制系統提供管制服務能力來描述。

終端區管制系統的主要目標是保障終端區空域內的航空器快速、安全、有序的運行。因此，可以通過空中交流的快速、有序、安全的程度來反映終端管制系統管制服務能力，評價終端區管制系統運行效率。本文從終端區管制單位的運行實際出發，結合文獻[11-13]充分考慮指標的典型性和可采集性，對終端區管制系統運行效率評價指標進行篩選、歸納和總結。終端區管制系統運行效率評價指標因素眾多，將同類指標映射為同屬性效率因子，每個屬性對應管制運行過程中所關心的效率的一個方面。因此，從延誤性、業務量、管制員工作負荷、終端區擁擠程度以及安全性五個方面構建終端區管制系統運行效率評價指標體系，如表1所示。

表1 終端區管制系統運行效率評價指標體系

各指標定義如下：

A1、A2、A3為由于航班延誤的致因較多，在終端區運行效率評估時，只考慮由管制原因導致的進離場延誤架次和延誤時間。

A4、A5為由于離場航空器都按照標準儀表離場程序運行，管制員不需要過多進行調配，而進場航空器需要管制員不斷地調整其速度、航向、高度來引導進場飛行，因此選擇終端區進場效率來衡量終端區管制系統運行效率。終端區進場效率定義為：進場效率=1-額外進場時間/暢通進場時間，其中額外進場時間=總進場時間-暢通進場時間。

B1為經由終端區各邊界點進出的小時流量。

B2、B3為B1中包含的起飛和著陸航班的小時流量。

C1為進近各扇區的管制員工作負荷。根據管制負荷直接測度法，假設管制員平均通話時間為t1，發布每條指令的思考時間t2=1.5 s，在工作時間段t內，共發出n條指令的工作負荷為：w=(nt1+nt2)/t×100%。

C2為指揮架次和通話總時長之比。

C3為通話總時長和值班時長之比。

D1、D2為航班的排隊長度指等待排序的航空器架次。

D3為跑道的飽和度。已知跑道的實際容量Ccapacity，D1=B2+B3/Ccapacity。

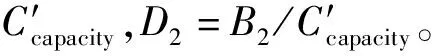
E1為根據自動化系統監視到的航空器4D航跡信息，實時監測航空器危險接近態勢，得出終端區內航空器內的間隔沖突告警。沖突性指標監控航空器間隔標準，反映管制員的間隔情況，是反映運行效率的重要前提和依據。

2 終端區管制系統運行效率評估模型構建

基于三角模糊熵-VIKOR法的終端區管制系統運行效率評估，實質上就是綜合運用三角模糊數法和熵權法求出主、客觀權重，利用最小相對信息熵的原理得到組合權重，增大評估指標間的差異性，根據VIKOR法的原理，計算終端區管制系統運行效率指數值，對終端區管制系統運行效率進行量化評價。

2.1 指標打分及標準化處理

對不同指標進行標準化處理就為了是使不同指標具有可比性和一致性。“終端區航班小時流量”等指標為正向指標，指標指數值越大越優。“終端區進場因管制原因延誤架次率”等指標為負向指標，指標指數越小越優。設Vij為第j個評估時段終端區管制系統內第i個評估指標值，n為待評估時段數量，一致性處理后的值為dij，正、負向指標的打分公式如下：

(1)

(2)

對所有指標進行標準化處理后，得到標準化矩陣D:

(3)

2.2 指標賦權

2.2.1 熵權法權重確定

根據熵權的定義，熵權值越大，該指標在效率評估中的作用越大；反之，熵權值越小，該指標在效率評估中的作用越小[14]。熵值法確定指標權重的方法如下：

(1)計算第i個指標，第j個評估時段的特征比重zij。

(4)

(2)根據熵值公式，計算第i個評估指標的熵值。

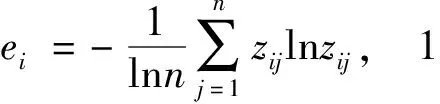
(5)

(3)假設評估指標的熵權集α=[α1,α2,…αm]T，第i個指標的熵值權重為

(6)

2.2.2 三角模糊法權重確定

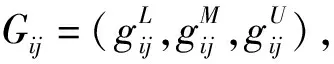
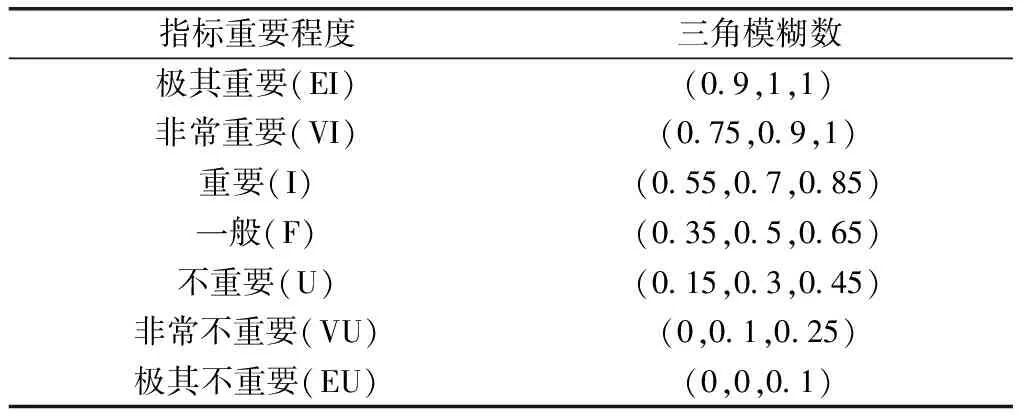
表2 指標重要程度及對應三角模糊數

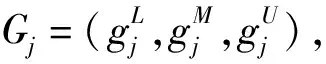
(7)

(3)采用加權平均法對三角模糊數進行去模糊化，評估指標j的重要性精確評價值為

(8)

(4)設三角模糊權重集為β=[β1,β2,…,βm]T，將其歸一化處理后得到第j個指標的模糊權重：

(9)

2.2.3 最小相對信息熵確定組合權重

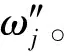
(10)

用拉格朗日乘子法求解式(10)得到組合權重wj：

(11)

式(11)利用幾何平均數的方法，避免了在組合賦權過程中增加其他附加信息。

2.3 基于VIKOR的終端區管制系統運行效率評估模型

VIKOR是由Opricovic等基于折衷優化思想，并考慮正負理想解距離之間的相對重要性，提出的用于解決復雜系統多準則評價的方法[16]。終端區管制系統運行效率的評估是典型的多屬性決策問題，因此，選擇VIKOR法，構建終端區管制系統運行效率評估模型。

基于VIKOR法的終端區管制系統運行效率評估模型，具體步驟如下。

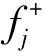
(12)

(13)

式中：Ωb是效益型指標集合；Ωc是成本類指標集合。效益型指標為A5、B1、B2、B3、C3，而包含A1、A2、A3在內的其余11個指標為成本型指標。

(2)計算各個評價對象的群體效用值Si和個體遺憾值Ri。

群體效益表示第i個方案到正理想解的加權距離，Si越小，代表群體效益越好，待評價的對象越優秀。

(14)

將第i個評價對象的最大遺憾值記為Ri，評價對象的個體遺憾值越小，評價對象越優。

(15)

式(15)中：ωj表示前文求得的第j個指標的權重。

(4)計算終端區管制運行效率折衷可行解Qi：

(16)

(5)計算終端區管制運行效率指數值。

折衷可行解Qi是待評價方案與理想解的距離，取值的范圍在[0,1]之間，Qi值越小，效率越高。為了使評價值更符合生活實際，需對Qi逆向修正，本文定義終端區管制運行效率指數Ej，計算公式為

Ej=1-Qj

(17)

則可根據Ej大小進行排序，對不同時段終端區管制系統運行效率進行比較，Ej越大，管制效率越高。

3 實例分析

3.1 實例情況

選取中國某機場的終端區作為研究對象，采用雙跑道隔離平行運行模式，該運行模式下，開設APP(S)和APP(N)兩個雷達管制服務扇區。終端區邊界設有5個進場點和4個出口點，其中，DOREX、MIKOS為進離場用點。以北京時間整點小時做時間段，選取該終端區某典型日8:00—22:00間的14 h段作為評價對象進行管制系統運行效率評估。

3.2 計算結果

根據三角模糊數法和熵權法求得主客觀權重，然后利用最小相對信息熵法求得組合權重，結果如表3所示。

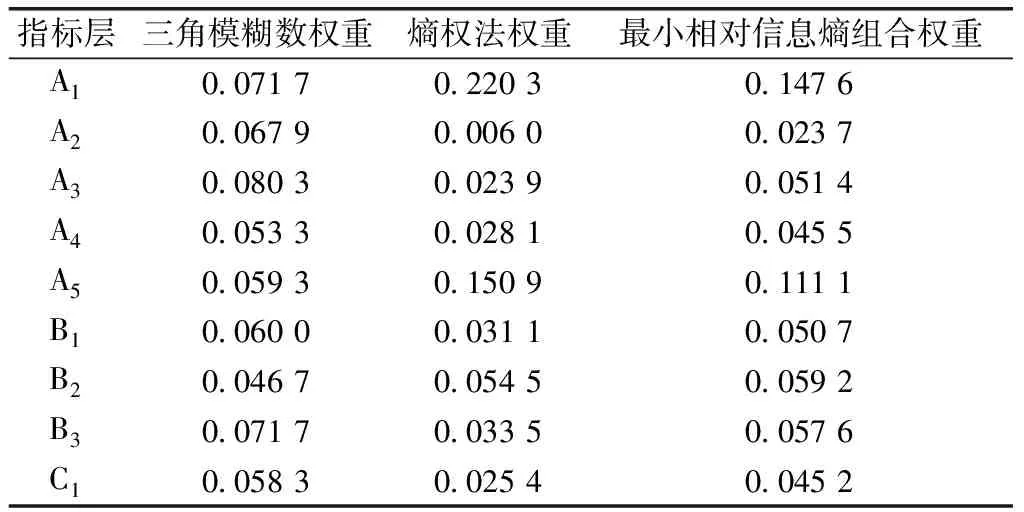
表3 評價指標標準權重

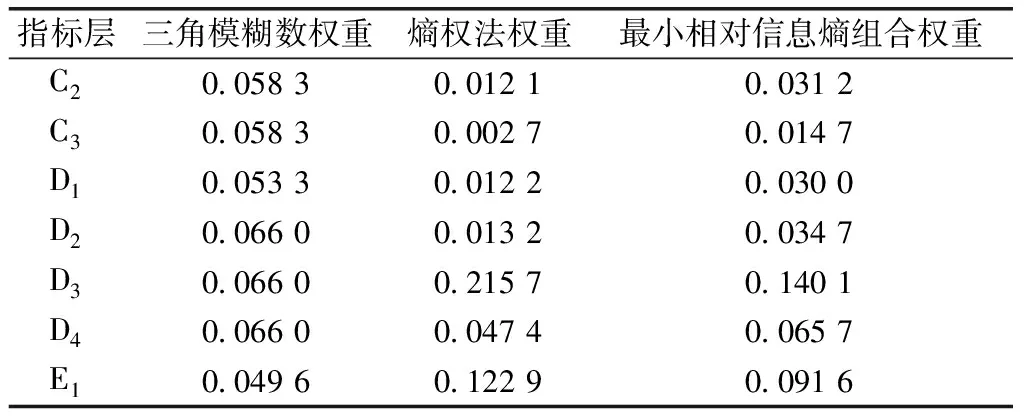
續表3

對原始數據進行標準化處理，結合指標的綜合權重，計算14個時段的群體效益值Si和個體遺憾值Ri，取v=0.5，計算折衷可行解Qj，最后計算終端區管制運行效率指數Ej，并根據Ej值進行遞減排序。評價結果如表4所示。

3.3 結果分析

由表4可知，VIKOR法和GRA-TOPSIS法所得到的同一時段終端區管制系統運行效率評價結果基本一致，排名位次差均不超過2，利用Spearman等級相關法，得到兩種方法的相關系數為0.949(P<0.01)，該結果表明這兩種評價法的關聯度極高，說明兩種方法所得評價結果具有較高的一致性，因此VIKOR評價法的計算結果是充分合理的。

此外，VIKOR法和GRA-TOPSIS兩種方法所得的終端區管制系統運行效率綜合評價值的極差分別為0.869 3和0.298 7，變異系數分別為0.486 0和0.170 9。極差越大，評價結果的分辨水平越強，離散程度越高。顯然，VIKOR法的評價值極差和變異系數均大于GRA-TOPSIS法，因此，VIKOR法所得到的綜合評價值相較于GRA-TOPSIS法，評價結果分布更加均勻合理，相鄰排序間評價值差異更明顯，更有利于直觀區分各時段終端區管制系統運行效率水平，對終端區管制系統運行效率評價有較強的適宜性。

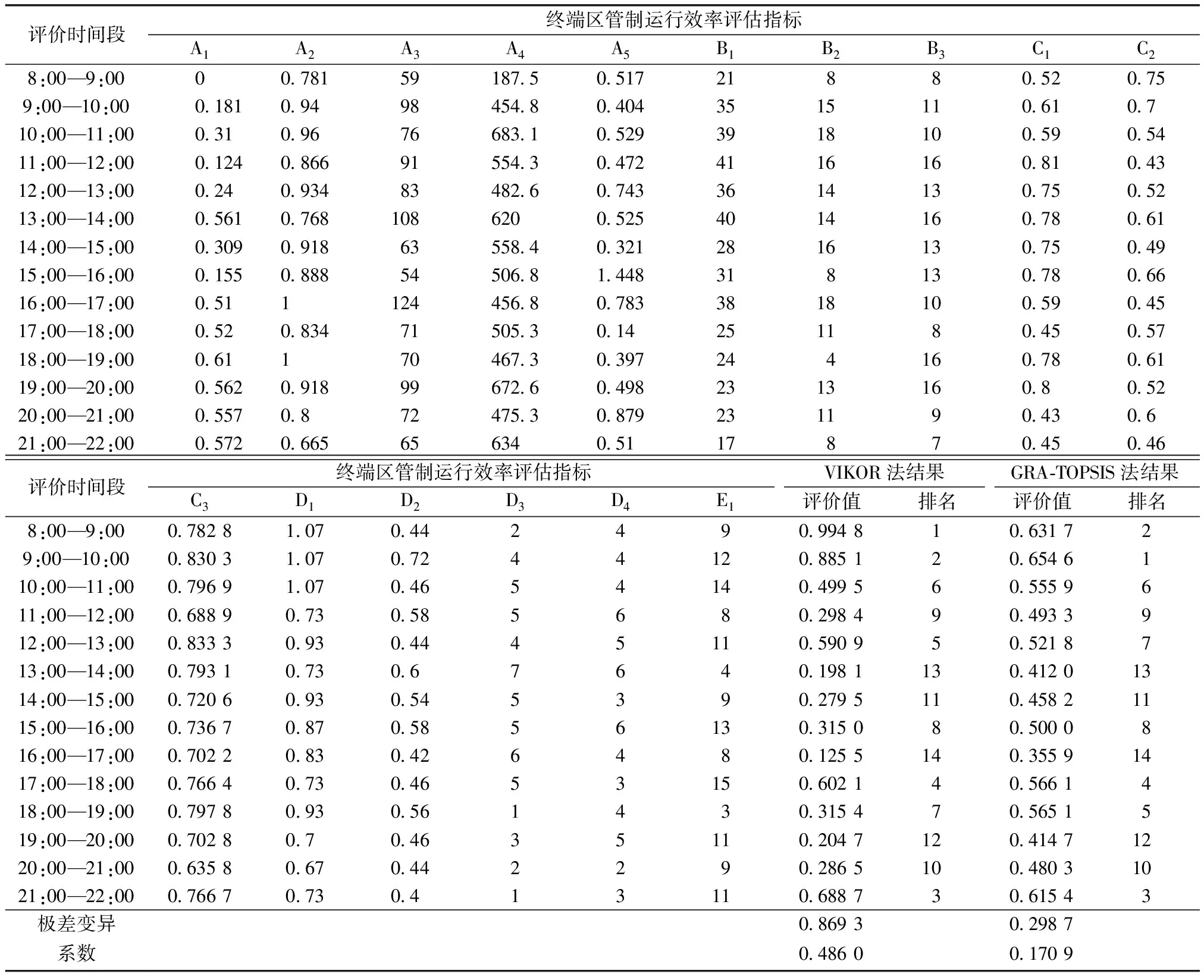
表4 某典型日某終端區8:00—22:00管制運行效率評估指標原始數據及評估結果

此外，在確定主觀權重時，選擇三角模糊數法。由圖1可知，通過層次分析法(analytic hierarchy process，AHP)和三角模糊數得到的指標權重對比可知，三角模糊數確定主觀權重時，通過語言變量對評價值進行模糊處理，更符合人的思維，得出的指標權重分布更平均，更加合理。

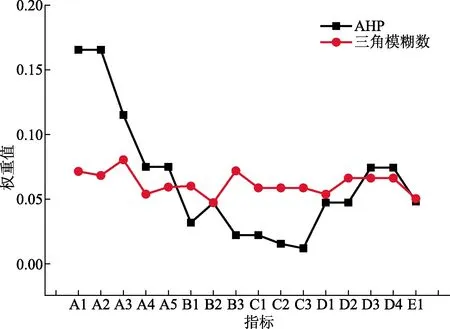
圖1 層次分析和三角模糊數主觀權重比較

由此可知，基于三角模糊熵-VIKOR法的終端區管制系統運行效率評估模型是合理且適宜的，根據當日終端區管制運行狀況，綜合評價得出如下結果。

(1)當日8:00—9:00、9:00—10:00這兩個時段的終端區管制運行效率指數較小，管制運行效率較高。根據資深管制員經驗，在這個時間段內，航班量較少，管制員工作負荷較低，由于早晨出港航班量較多，空中交通流較為穩定，空域利用率較高，不易出現飛行沖突，終端區管制系統整體運行效率較高，運行較為穩定。

(2)在13:00—14:00、16:00—17:00、19:00—20:00這三個時段運行效率最低。首先，這幾個時段內航班量較大，終端區內交通流復雜，排隊航班較多，跑道和終端區管制扇區始終處于飽和狀態，導致飛行延誤的發生，并且管制員工作負荷增加，不安全事件頻發，管制系統運行效率較低，符合管制運行實際。

4 結論

從終端區管制系統實際運行過程出發，建立終端區管制系統運行效率評估指標體系；接著采用三角模糊數法得到評估指標的主觀權重，利用熵權法得到客觀權重，并利用最小相對信息熵法得出了組合權重。利用VIKOR法，計算出終端區管制系統運行效率指數值，對終端區管制系統運行效率進行量化評估。根據算例，得到如下結論。

(1)三角模糊數法確定主觀權重時，克服了AHP法主觀賦權時的主觀臆斷性，賦權過程更符合人的思維，得到的主觀權重更加合理。利用最小相對信息熵法得出組合權重，最大限度地保留原始數據，同時使專家評分的客觀性提高，指標權重量化結果更加合理。

(2)VIKOR法和GRA-TOPSIS法對同時段的終端區管制系統運行效率評估結果相關系數高達0.949，評價結果具有極高的一致性。但基于三角模糊熵-VIKOR法的率評估方法，評價結果分辨度更強，離散程度更高，評價結果更加均勻合理。且評價結果與管制運行實際結果相符，是有效可行的評估方法。

在對終端區管制系統運行效率準確評價之后，如何找出對終端區管制系統運行效率有重要影響的因素，并得出相應的效率提升策略，有待進一步研究。