強可能性與弱必然性的邏輯

陳佳

1 哲學背景與動機

是什么讓現實世界區別于其他可能世界？有些人主張，現實世界是實在的，其他的可能世界只不過是語言的構造。（[2]，第9 頁）D.Lewis 等模態實在論者堅持，所有可能世界都同樣是實在的，在這點上現實世界和其他可能世界沒有區別。（[10]，第2 頁）無論如何，我們至少可以有一條簡單有效的標準以幫助我們識別出現實世界，這條標準本質地使用了第一人稱索引詞，所以可稱之為第一人稱標準：

我們所生活的世界是現實的，其他的世界（如果它們確實存在的話）不是現實的。因此，“豬會飛的世界”、“日本征服中國的世界”、“希拉里當選第45 屆美國總統的世界”等這些世界頂多是可能的，但它們不是我們所生活的世界，因而不是現實的。我們只與現實世界中的事物具有時空聯系，但與其他可能世界中的事物不具有時空聯系。然而有趣的是，人們常常會關心那些非現實的可能世界，甚至著迷于此。人與動物以及人工智能的一個區別是人能夠想象非現實的情境。這種反事實思維不僅能給人帶來精神愉悅（許多藝術都可以被視為是一種想象活動），而且對于人類文明的延續和發展至關重要。比如Lewis（[9]）和Williamson（[18]）分別用反事實推理來刻畫因果和模態概念，而掌握這兩種概念對于人類進行決策實踐和科學探究而言無疑都是必要的。

可能世界思想為模態邏輯提供了標準語義學。一個命題如果它在現實世界中是真的，則它是實然的；如果它在某個現實世界可及的可能世界中是真的，則它是可能的；如果它在所有現實世界可及的可能世界中都是真的，則它是必然的。現實世界相對于自身而言也是一個可及的可能世界，所以實然性蘊涵了可能性。然而，若某命題的可能性僅僅出于其實然性，那么這種可能性不免是有些平庸的。當我們討論可能性時，我們更關心那些非現實的可能世界中有哪些命題成立。因此，本文將考察兩種新的真勢模態性質：強可能性和弱必然性。一個命題是強可能的，如果它在某個非現實的但可及的可能世界中是真的；它是弱必然的，如果它在所有非現實的但可及的可能世界中都是真的。不難發現，強可能性蘊涵了可能性，必然性蘊涵了弱必然性。此外，強可能與弱必然性互為對偶。這就是說，一個命題是強可能的，當且僅當它的否定不是弱必然的；它是弱必然的，當且僅當它的否定不是強可能的。在邏輯性質上，強可能性類似于可能性，弱必然性類似于必然性，但它們也具有顯著的不同：實然性不蘊涵強可能性，弱必然性不蘊涵實然性，而且弱必然性不蘊涵強可能性。

與強可能性概念（以及弱必然性概念）直接相關的是他世界模態（modality for other-world），也被稱為不等性模態（modality of inequality）。對于世界w而言，命題p在他世界上成立，當且僅當存在一個不同于w的世界v使得p在v上成立。他世界模態的概念起源于von Wright 對空間邏輯的研究1von Wright（[19]）稱之為地點的模態邏輯（a modal logic of place）。，在此語境下它表達的意義是（某命題）在非此地的其他某個地點上（elsewhere）成立（對elsewhere 算子的研究，參見[15，16，19]）。類似地，在時態邏輯語境下它表達了（某命題）在非此時的其他某個時刻上（elsewhen）成立。2作為“elsewhere”在時態上的對應物，“elsewhen”是Segerberg 所生造的英語詞。Segerberg認為刻畫“elsewhere”和“elsewhen”的是同一種邏輯，更詳細的討論見[13，15，16]。在時態邏輯語言上了加入不等性算子（等同于“elsewhen”算子），從而能夠刻畫更加豐富的時間結構（比如嚴格線序）。他世界模態也可以作為一種真勢模態來理解，比如Humberstone（[8]）認為，他世界模態邏輯為區分模態實在論、反實在論以及不可知論提供了恰當的邏輯基礎，而這是普通的模態邏輯所做不到的。他世界模態與強可能性模態的聯系和區別是顯而易見的。一方面，當可能世界之間的可及關系是近全通關系時（即任意兩個不同的可能世界之間都是可及的），他世界模態與強可能性模態是等價的，因此可以將他世界模態邏輯視為強可能性模態邏輯的特例。事實上，他世界模態邏輯的極小系統（即[19]中的系統SW B+A5，[16]中的系統KAB，[13]中的系統DL以及[8]中的系統KB4′）等價于下文所給出的系統4（及其等價系統5）。另一方面，他世界模態不涉及可能世界之間的可及關系，或者說它只涉及一種可及關系，即不等關系3在不等關系下，兩個世界w 和v 是可及的，當且僅當wv。，而強可能性模態則可以容納任意可及關系。從多模態邏輯角度來看，他世界模態只是一種模態，而對任何可能型模態而言（包括形而上學可能、物理可能、認知可能、置信可能、道義可能等等）都存在與之對應的一種強可能型模態，這也使得強可能性模態具有更寬廣的應用前景。

強可能性和弱必然性概念也啟發了我們去考察其他相關的真勢模態。萊布尼茨提出：有些實然命題不僅是真的，而且是必然的；有些實然命題卻僅僅是偶然的，“它們的反面是可能的”。4參見萊布尼茨《單子論》第33 節，中文譯文見[20]，第482 頁。按照可能世界語義的分析，萊布尼茨所謂“事實的真理”指的是這樣的命題：它在現實世界中是真的，但在某個非現實的可及世界中不真，即它的否定是強可能的。萊氏“事實的真理”在當代文獻中也被稱為偶真性（accident）5與偶真性容易混淆的一個概念是偶然性（contingency），它是與非偶然性（non-contingency）相對偶的概念。稱命題p 是偶然的，指的是p 及p 的否定都是可能的。關于偶然性邏輯，可參考[3，5，7]以概覽這個領域。，它與本質性（essence）構成了一組對偶概念，它們作為非正規的真勢模態而受到了邏輯學家的關注（參見[4，11，17，21]）。盡管在相關文獻中，偶真性與本質性由可能性和必然性所定義，但實際上它們也可以被強可能性和弱必然性定義。不僅如此，利用強可能性和弱必然性模態我們還可以定義出一種新的偶然真理概念：稱一個命題是“超偶然真理”，當且僅當它在現實世界中是真的，但它在任何非現實的可及世界中都不真，即它的否定是弱必然的。6值得與“超偶然真理”概念加以比較的還有Pan 和Yang（[12]）提出的強偶性概念（strong accident）。稱一個命題具有強偶性，當且僅當該命題成立但其否定必然不成立。顯然，任何滿足強偶性的命題都是“超偶然真理”，但反之不必然。“超偶然真理”反映的是那些幾乎不可能為真但偏偏竟然成真的命題，因此可以說它們是“奇跡”，構造關于“奇跡”的邏輯將是一個有趣的探索方向。

我們關心強可能性和弱必然性的另一個動機來自于動態邏輯。（[6]）模態邏輯除了是刻畫可能性和必然性的，它也是刻畫變化的。在這種解釋之下，菱形算子代表的是在某種動作之后系統狀態發生了轉移，但這種解釋并不排除“原地踏步”式的狀態轉移，即經過某種動作之后狀態實際上未發生變化。與之對照的是，強可能性刻畫的是狀態轉變，即經過某種動作之后系統的狀態發生了變化。因此，強可能性在更嚴格的意義上刻畫了變化。

綜上所述，強可能性和弱必然性不僅在邏輯上是兩種新的真勢模態，在哲學上無疑也是頗具吸引力的重要概念。盡管如此，本文的目標主要在邏輯上而非哲學上，即對強可能性和弱必然性的邏輯（以下簡稱強可弱必邏輯）作一個初步但力圖系統的研究。本文的安排如下：第2 節給出強可弱必邏輯的形式語言和語義，提出了適用于強可弱必邏輯的互模擬概念，并將之運用于對強可弱必語言和模態邏輯語言以及一階語言的表達力比較；第3 節給出強可弱必邏輯的極小公理系統以及在各框架類上的擴張系統，并證明它們的可靠完全性；第4 節考慮了在同時含有必然和弱必然算子的雙模態語言下的公理刻畫，給出了兩個具有普遍性的橋接公理但又指出了它們的局限性。

2 強可弱必邏輯：語言、語義和表達力

2.1 語言和語義

令Φ 是一原子命題集合，定義形式語言L(?)為：

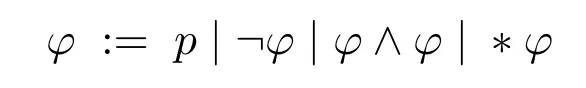
其中p ∈Φ。當?取弱必然算子時，那么得到的是強可弱必邏輯語言SW；當?取必然算子時，得到的是單模態邏輯語言ML；當?既可以取也可以取時，得到的是帶必然算子和弱必然算子的雙模態邏輯語言ML+。給定公式φ和ψ，規定以及分別是?(?φ ∧?ψ)，?φ ∨ψ，的縮寫。直觀上，以及分別可以讀作：“φ是弱必然的”，“φ是強可能的”，“φ是必然的”以及“φ是可能的”。

一個Kripke 模型（以下簡稱模型）是一個三元組M=(W，R，V)，其中W是一個非空的可能世界集合，R?W2是W上的二元可及關系，賦值函數V:Φ2W給每個原子命題指派一個滿足它的可能世界集合。二元組F=(W，R)被稱為M所基于的框架。對于w ∈W，稱(M，w)是一個點模型。公式在點模型上的真值條件被歸納定義為：

由上述定義不難得出的真值條件：

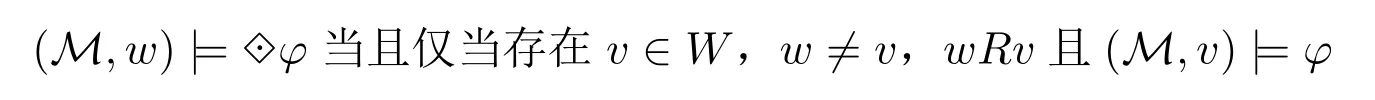
這就是說，在w上是真的，當且僅當存在某個w可及的但又不同于w本身的可能世界v，φ在v上是真的，即在世界w中φ是強可能的。

給定可及關系R，令R?={(w，v)，那么的真值條件可以被重新表述為必然型模態的“常規”形式：

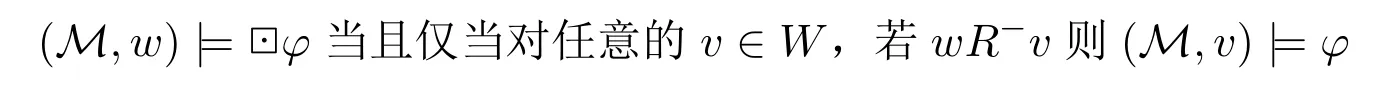
這表明強可能性算子和弱必然算子在邏輯性質上仍然是一種正規模態。

對于公式集Γ 和公式φ：如果Γ 中的所有公式都在點模型(M，w)上是真的，那么稱(M，w)滿足Γ；令X是一框架類或模型類，如果對所有X中的模型M，以及M中的世界w都有(M，w)|=Γ 蘊涵(M，w)|=φ，那么稱在X上φ是Γ 的語義后承，記作Γ|=X φ。如果，那么稱在X上φ是有效的，并簡記為。特別地，當X是全部框架構成的類（或全部模型構成的類）時，Γ被簡記為Γ|=φ，并稱φ是Γ 的語義后承，同樣地被簡記為，并稱φ是有效的。

通過限制可及關系R的性質，我們可以得到許多有趣的框架（模型）類。本文主要考察以下常見的框架（模型）類，其中由同樣的可及關系性質所規定的框架類和模型類使用了同樣的記法，在下文中易由語境辨別出它們指稱的是框架類還是模型類：

記法 名稱 可及關系R的性質

D持續框架（模型）類 持續性：?x?y(xRy)

T自反框架（模型）類 自反性：?x(xRx)

A禁自反框架（模型）類 禁自反性：?x(?xRx)

B對稱框架（模型）類 對稱性：?x?y(xRy →yRx)

4傳遞框架（模型）類 傳遞性：?x?y?z(xRy ∧yRz →xRz)

5歐性框架（模型）類 歐性：?x?y?z(xRy ∧xRz →yRz)

S4自反傳遞框架（模型）類 自反性+傳遞性

S5等價框架（模型）類 自反性+對稱性+傳遞性

此外，由所有框架（模型）構成的類被記為K。對于框架（模型）類X和Y，我們用XY表示它們的交集。

2.2 與模態邏輯語言的表達力比較

給定模型類X，如果對于語言L2中的任何公式φ都存在語言L1中的某個公式ψ，使得，那么稱在X上L1的表達力至少和L2一樣強，記作。如果但，那么稱在X上L1的表達力嚴格強于L2，記為。如果且，那么稱在X上L1和L2的表達力一樣強，記作。如果且，那么稱在X上L1和L2的表達力不可比較，記作。

當可及關系R滿足禁自反性時，那么R=R?，因而對任何公式φ都有以及。此時，強可能性坍塌為可能性，必然性坍塌為弱必然性。這說明在禁自反框架中，強可弱必邏輯語言和模態邏輯語言的表達力一樣強，即SW ≈A ML。

當可及關系R滿足自反性時，那么R=R?∪{(w，w)|w ∈W}，因而不難驗證對任何公式φ都有并且。因此可以用強可能算子和弱必然算子來定義可能算子和必然算子。這說明在自反模型類中，強可弱必邏輯語言表達力至少和模態邏輯語言一樣強，即。事實上下文（定理2）還將進一步表明，在自反模型類上強可弱必邏輯語言的表達力嚴格強于模態邏輯語言。

在更多的模型類中這兩種語言的表達力不可比較，其證明思路是考察它們分辨不同模型的能力。給定語言L，稱點模型(M，w) 和(M′，w′) 是L等價的，記作(M，w)≡L(M′，w′)，如果對任何L公式φ都有(M，w)(M′，w′)。當(M，w)≡L(M′，w′)時，我們無法利用語言L來分辨這兩個模型。一個語言的表達力越強，它分辨模型的能力也越強。顯然，如果可以構造出兩個基于X的點模型(M，w)和(M′，w′)，使得(M，w)≡L1(M′，w′)但(M，w)2(M′，w′)，那么L1X L2。

如何發現兩個模型是否關于某個語言等價？在模態邏輯中，互模擬為我們發現模態不變性提供了基礎。但是相對于我們的新語義，需要對互模擬關系加以修訂。

定義1(互模擬和3互模擬).給定模型M=(W，R，V)和M=(W′，R′，V ′)。稱二元關系Z?W×W′是M和M′之間的互模擬，記為Z:，如果下述條件成立：

(1) 如果wZw′那么w和w′滿足同樣的原子命題；

(2) 如果wZw′，wRv并且wv，那么存在（M′中的）v′使得vZv′，w′R′v′并且w′v′；

(3) 如果wZw′，w′R′v′并且w′v′，那么存在（M中的）v使得vZv′，wRv并且。

如果存在Z使得它是將M中的w以及M′中的w′連接起來的3·互模擬，那么稱w和w′之間互相似，記作。

若將上述條款(2)和(3)修改為：

(2′) 如果wZw′且wRv，那么存在（M′中的）v′使得vZv′并且w′R′v′；

(3′) 如果wZw′且w′R′v′，那么存在（M中的）v使得vZv′并且wRv；

那么我們得到了通常的互模擬關系，這里不妨把它稱做互模擬關系。

例1.考慮如下模型，其中{w1，w2，w3，w4，w5，w6}滿足同樣的原子命題，{w7，w9}滿足同樣的原子命題，{w8，w10}滿足同樣的原子命題，其余的世界所滿足的原子命題不盡相同：

注意這些模型中，除了M1其他都滿足持續性，除了M2其他都滿足對稱性，除了M5其他都滿足傳遞性以及歐性，并且只有M3、M4和M6滿足自反性。不難驗證，，其余的世界兩兩不互相似；，其余的世界兩兩不3互相似。

從例1 可以看出，互模擬和互模擬相互不蘊涵對方。但是它們仍然存在著緊密的聯系：

命題1.對于模型M=(W，R，V)，令M?=(W，R?，V)。那么對任何點模型(M，w)和(M′，w′)，當且僅當。

證明.只要注意到對任何Z?W×W′都有：

那么結論顯然成立。

互模擬是通向模態不變性的階梯，因為存在著下述定理：

定理1.對任意點模型(M，w)和(M′，w′)，

證明.(1)和(2)的證明請參考[1]第67 頁定理2.20，第69 頁定理2.24。(3)和(4)仿照之亦容易證明。

因此，對于有限模型而言，互相似等同于SW等價，互相似等同于ML等價。這樣在例1 中，我們就構造出了一些ML等價但SW不等價的模型，以及一些SW等價但ML不等價的模型，從而我們得到了下述結論：

定理2.對模型類X ∈{T，T B，S4，S5}，有。對模型類X ∈{K，D，B，4，5，45，DB，B45}，有SW?X ML。

2.3 與一階語言的表達力比較

每個Kripke 模型都可以被自然轉化為一個一階模型，因此我們可以對模態語言和一階語言的表達力進行比較。眾所周知，在模型層面上模態語言是一階語言的互模擬不變片段。對于強可弱必邏輯也存在著類似的結果。

每個SW公式都存在著一個與之語義等價的一階對應公式，該公式被稱作原公式的標準翻譯，它含有且僅含有一個自由變元。令x是一個一階變元，標準翻譯STx是一個從SW公式到一階公式的映射，它被遞歸地定義為：

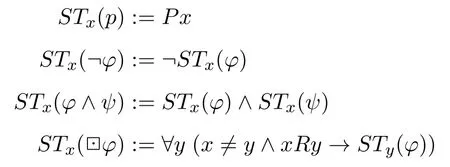
類似于van Benthem 刻畫定理的證明（[1]，第103 頁定理2.68）我們有如下的刻畫定理：

定理3(刻畫定理).令α(x)是一個一階公式。那么α(x)相對于互模擬不變，當且僅當它等價于某個SW公式的標準翻譯。

因此，在模型層面上強可弱必邏輯語言SW是一階語言的互模擬不變片段。

3 強可弱必邏輯：公理化與完備性

本節將給出強可弱必邏輯的極小公理系統以及它關于各種框架類的擴張系統，并證明它們的可靠完全性。這里先對一些必要的預備概念和引理作些說明。注意，在非指明的情況下本節所說的公式均指SW公式。

一個公理系統L 由若干公理和推理規則構成。如果只使用這些公理和推理規則能推導出公式φ的話，那么稱φ是L 的定理，記作Lφ。如果公式集Γ 中存在φ0，...，φn使得Lφ0∧···∧φn →φ，那么稱在L 下可由Γ 衍推出φ，記作ΓLφ。稱公式集Γ 是L 一致的，如果ΓLp ∧?p。如果L 是經典命題邏輯的擴充的話，那么對任何公式集Γ 和公式φ有：Γ∪{?φ}是L 不一致的，當且僅當ΓLφ。

證明某個公理系統L 相對于框架類F是完全的，其通常的思路是先證明對于每個L 一致的集合都存在一個基于F的點模型(M，s)，使得(M，s)滿足Γ。這時，若有Γ，那么Γ∪{?φ}不可被任何基于F的點模型滿足，從而Γ∪{?φ}是L 不一致的，因此有ΓLφ。這說明了L 關于框架類F是完全的。

典范模型方法是為一致集尋找滿足它的模型的標準方法，其思想是利用邏輯系統的語形特征來構建語義模型。典范模型方法非常依賴于極大一致集的概念。給定公理系統L，稱公式集Γ 是L 極大一致集，當且僅當(i)Γ 是L 一致的，(ii)Γ 是極大的，即對所有L 一致集Γ′，若Γ?Γ′，那么Γ=Γ′。所有L極大一致集構成的集合被記為MCS(L)。關于極大一致集，有如下重要性質：

引理1.令L 是一個包含經典命題邏輯的擴張系統，Γ 是任意L 極大一致集，那么

(1) 任何L 一致集都可以擴充為L 極大一致集；（Lindenbaum引理）

(2) 對任何公式φ，或者φ ∈Γ，或者?φ ∈Γ；

(3) 若φ →ψ，φ ∈Γ，那么ψ ∈Γ；

(4)φ0∧···∧φn ∈Γ 當且僅當對所有i ∈{0，...，n}，φi ∈Γ；

(5)φ0∨···∨φn ∈Γ 當且僅當存在i ∈{0，...，n}使得φi ∈Γ。

3.1 極小系統

引理2.對任何L 極大一致集Γ，若，那么是L 一致的。其中，。

集合(Γ)也被稱為Γ 的去弱必然化集。

我們將嘗試為L 構建典范模型。對此，一個自然的思路是：用MCS(L)作為其典范模型的可能世界集，并規定L 極大一致集Γ′對于L 極大一致集Γ 是可及的，當且僅當L 的去弱必然化集合(Γ)包含于Γ。但這樣構建的典范模型是不可行的。考慮集合S=，當它是L 一致的時候，它可以被擴張為L 極大一致集Γ。從Γ 所包含的命題來看，它聲稱它有且僅有一個非它自身的可及世界，而這個世界所包含的命題又和Γ 完全相同。然而作為極大一致集，這個和Γ 包含了一樣的命題的可能世界又只能是Γ 本身，矛盾！

對此的解決方法是為每一個“有問題的”L 極大一致集建立一個它的副本。7本文建立副本的技巧與文獻[14，16]中的“bulldozing”方法類似。所謂“有問題的”L 極大一致集，指的是那些包含所有形如的公式的L 極大一致集。這樣的L 極大一致集之所以是“有問題的”，因為它暗示了存在某個它可及的世界，這個世界不同于它，但又和它滿足完全相同的命題。因為形式上是模態邏輯的(T)公理，所以我們將所有“有問題”的L 極大一致集所構成的集合記為T(L)，并令=MCS(L)/T(L)。由于極大一致集的性質（引理1），容易證明：對所有L 極大一致集Γ，Γ∈T(L)當且僅當(Γ)?Γ。

語言SW對于所描述的世界是否滿足自反性無所說，即我們不能通過它的語句來判斷某個世界是否是其自身的可及世界。這既為我們構造典范模型造成了一定的障礙，但也提供了一些靈活性。這就是說，我們可以自己調整可及關系，使之滿足自反性或不滿足自反性。這里我們希望構造的是滿足自反性的典范模型。

定義2(自反典范模型).給定任意K 的一致正規擴張L，定義L 的自反典范模型為RC(L)=(W，R，V)，其中

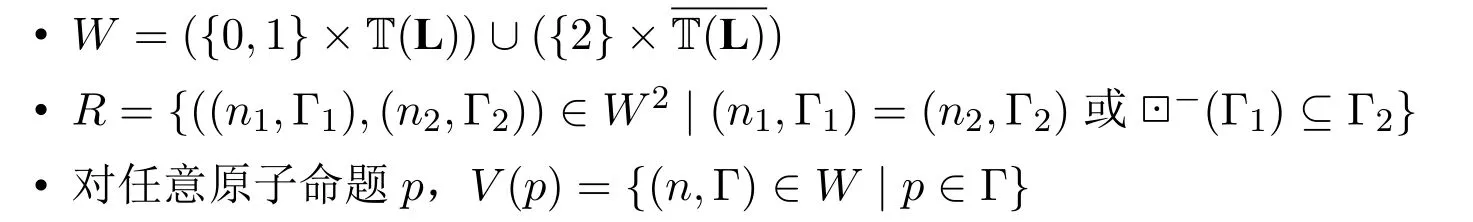
注意，根據我們對R定義，顯然R是自反的。對于(n，Γ)∈W，參數n表明了L 極大一致集Γ 的性質：當Γ/∈T(L)時，n的取值只能是2，此時(2，Γ)沒有額外的副本；當Γ∈T(L)時，n取值為0 或1，此時(0，Γ)和(1，Γ)互為對方的副本。

引理3(RC(L) 的真值引理).給定任意K 的一致正規擴張L，令RC(L)=(W，R，V)是其自反典范模型，那么對任意(n，Γ)∈W以及任意公式φ都有：

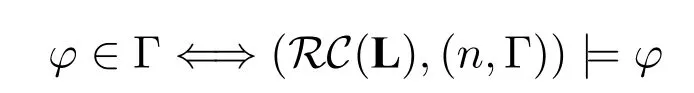
證明.我們對公式結構歸納，布爾情況易證，這里只考慮φ=的情況。

首先，當Γ 時，那么(Γ)，因而由定義2 可知對W中的任意元素(m，Γ′)(n，Γ)，若(n，Γ)R(m，Γ′)，那么α ∈Γ′，再由歸納假設，有(RC(L)，(m，Γ′))。由的真值條件可知，(RC(L)，(n，Γ))。

其次，當/∈Γ 時，由/∈Γ 和引理2 可知，(Γ)∪{?α}是L 一致的，從而可以擴充為極大一致集Γ′。我們這時分兩種情況討論：

? 情況1：n=2。此時Γ/∈T(L)，從而存在公式β使得2·β ∈Γ 但β/∈Γ。因為Γ，所以β ∈Γ′。又因為β/∈Γ，從而ΓΓ′。當Γ′ ∈T(L)時，我們令m=0，否則令m=2，因而由定義2 可知(m，Γ′)∈W。因為(Γ)?Γ′，所以(n，Γ)R(m，Γ′)；因為ΓΓ′，有(n，Γ)(m，Γ′)；因為?α ∈Γ′，由歸納假設，有(RC(L)，(m，Γ′))α。因此，根據的真值條件，有(RC(L)，(n，Γ))。

? 情況2：n ∈{0，1}。此時Γ∈T(L)，即(Γ)?Γ。當Γ′ ∈T(L)時，那么令m=1?n，否則令m=2。因此有并且(m，Γ′)∈W。從而我們同樣有(n，Γ)R(m，Γ′)，(n，Γ)(m，Γ′)，但(RC(L)，(m，Γ′))α。因此，(RC(L)，(n，Γ))。

當我們將引理3 運用到系統K 上時，我們為每個K 極大一致集Γ 找到了一個滿足它的模型：當Γ∈T(K) 時，有(RC(K)，(0，Γ))Γ；當Γ/∈T(K)時，有(RC(K)，(2，Γ))Γ。而且，這個模型滿足自反性，從而也滿足持續性。又因為K 在全框架類上是可靠的，所以我們得到了如下的完備性結果：

定理4(K 的完備性).系統K 相對于全框架類K、持續框架類D和自反框架類T都是可靠完全的，即：對X ∈{K，D，T}，以及任意公式集Γ 和公式φ，ΓKφ當且僅當Γ。

在下一節中，我們將引理3 運用于更多的擴張系統上去。

3.2 擴張系統

本節將要考察如下的特征公理（模式）和擴張系統:

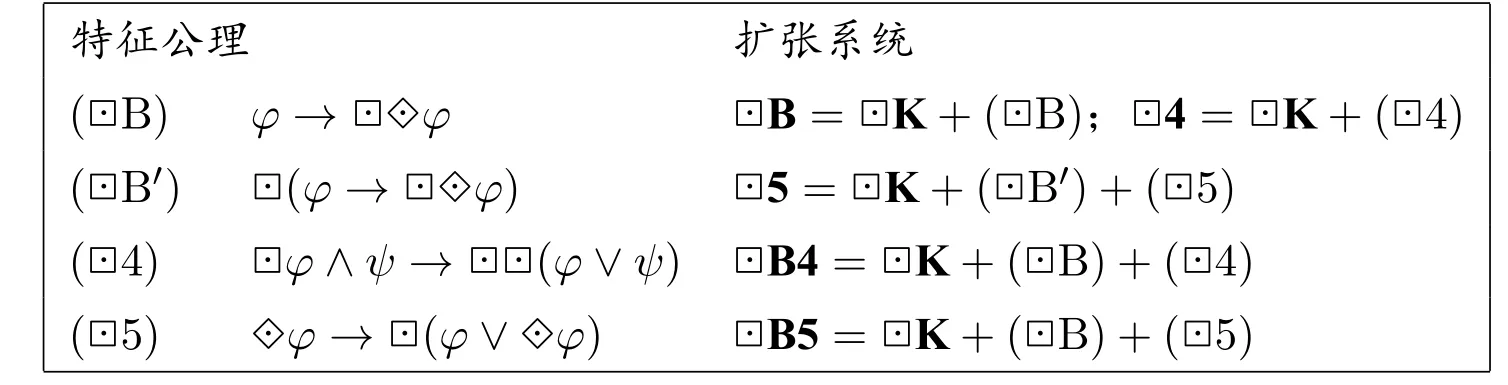
在證明擴張系統的語義完全性之前，我們需要對這些公理和系統的性質作簡要討論。首先，這些公理的命名會讓人自然聯想到模態邏輯的(B)、(4)以及(5)公理。我們知道(B)、(4)、(5)公理分別定義了對稱性、傳遞性以及歐性。8稱公式φ 定義了框架性質P，指的是對所有框架F，F 具有性質P 當且僅當φ 在F 上有效。那么公理(B)、(B′)、(4)以及(5)是否也定義了相應的框架性質呢？不難驗證，除了(B)公理，它們所定義的框架性質要更弱一些。

命題2.

公理(B)定義了對稱性：?x?y(xRy →yRx)；

公理(B′)定義了弱對稱性：?x?y?z(xRy ∧yRz →zRy ∨x=y)；

公理(4)定義了弱傳遞性：?x?y?z(xRy ∧yRz →xRy ∨x=z)；

公理(5)定義了弱歐性：?x?y?z(xRy ∧xRz →yRz ∨x=z ∨y=z)。

這里作五點評論，其正確性請讀者自行驗證：(1) 系統B4 和系統B5是等價的；(2) 對于任何包含有(4) 的擴張系統，若將(4) 替換為(4′)：，那么得到的新系統與原系統是等價的；(3)對稱性蘊涵弱對稱性，傳遞性蘊涵弱傳遞性，歐性蘊涵弱對稱性以及弱歐性；(4)不存在SW公式能夠定義持續性、自反性、傳遞性和歐性；(5)盡管如此，模態語言仍然能夠定義弱對稱性、弱傳遞性和弱歐性（見命題3）。

命題3.存在模態公式可以定義弱對稱性、弱傳遞性和弱歐性，具體而言：

模態公式()定義了弱對稱性；

模態公式(φ ∨ψ)（或者）定義了弱傳遞性；

模態公式(ψ →φ)()定義了弱歐性。

通過以上討論，可得關于上述擴張系統的可靠性結果：

命題4.

接下來我們考慮這些擴張系統的語義完全性。我們希望能將引理3 運用于對這些系統的完全性證明上，這要求我們證明它們的自反典范模型滿足相應的框架性質。

引理4.對于系統4 的任意一致正規擴張L，其自反典范模型RC(L)=(W，R，V)都基于傳遞框架。

證明.我們假設(n1，Γ1)R(n2，Γ2) 且(n2，Γ2)R(n3，Γ3)，以此來證明(n1，Γ1)R(n3，Γ3)。當(n1，Γ1)=(n3，Γ3) 或者(n1，Γ1)=(n2，Γ2) 或者(n2，Γ2)=(n3，Γ3)時，因為RC(L)基于自反框架，我們立刻有所需結論，所以我們僅需考慮這三者兩兩不相等的情況，此時(Γ1)?Γ2并且(Γ2)?Γ3，而我們需要證明(Γ1)?Γ3。令φ是屬于(Γ1)的任意公式，即Γ。如果Γ1=Γ3，那么必然n13，因此有n1，n3∈{0，1}而且Γ1=Γ3∈T(L)，此時(Γ1)?Γ1=Γ3，即所需結論成立。如果Γ1Γ3，那么不妨假設ψ ∈Γ1而?ψ ∈Γ3。由公理(4)可知(φ ∨ψ)∈Γ1，又因為Γ1且ψ ∈Γ1所以有(φ ∨ψ)∈Γ1。因為(Γ1)?Γ2，所以(φ ∨ψ)∈Γ2，又因為(Γ2)?Γ3，所以φ ∨ψ ∈Γ2，再由于?ψ ∈Γ3，所以φ ∈Γ3。因為φ的任意性，所以有(Γ1)?Γ3，因而(n1，Γ1)R(n3，Γ3)。

引理5.對于系統B 的任意一致正規擴張L，其自反典范模型RC(L)=(W，R，V)都基于對稱框架。

證明.我們假設(n1，Γ1)R(n2，Γ2)，以此來證明(n2，Γ2)R(n1，Γ1)。當(n1，Γ1)=(n2，Γ2)時，因為RC(L)基于自反框架，所以結論直接成立。因此，我們考慮(n1，Γ1)(n2，Γ2)的情況，此時有(Γ1)?Γ2，而我們需要證明(Γ2)?Γ1。考慮任意公式φ，并假設φ/∈Γ1，這等價于?φ ∈Γ1。又由公理(B)有Γ1，因此Γ1。再由(Γ1)?Γ2，有Γ2，因此/∈Γ2。由φ的任意性，有(Γ2)?Γ1。

因此，RC(B)、RC(4)和RC(B4)（=RC(B5)）分別基于自反對稱框架、自反傳遞框架以及等價框架（即自反對稱傳遞框架），從而利用引理3（以及命題4）我們有如下的完備性結果：

定理5(B、4、B4、B5 的完備性).

(1) 系統B 相對于對稱框架類B、持續對稱框架類DB以及自反對稱框架類T B都是可靠完全的；

(2) 系統4 相對于傳遞框架類4、持續傳遞框架類D4以及自反傳遞框架類S4都是可靠完全的；

(3) 系統B4 及其等價系統B5 相對于對稱傳遞框架類B4（它等同于對稱歐性框架類B5）以及等價框架類S5都是可靠完全的。

目前為止都很順利，但是對于系統5 而言卻存在著麻煩，因為它的自反典范模型不滿足歐性。為此，我們需要為它構造新的典范模型，這個典范模型滿足歐性但不滿足自反性。我們的做法是對2·5 極大一致集進一步分類。首先定義ΛB=是任意SW公式}，再定義B(5)={Γ∈MCS(5)|ΛB?Γ}。因此若Γ∈B(5)，那么Γ 包含了公理(B):的所有代入例，從直觀上來講這樣的Γ 似乎“聲稱”自己滿足對稱性；反之那些B(5)以外的5 極大一致集，它們構成的集合被記為，則“聲稱”自己不滿足對稱性。另外，由于5 包含了公理(B′):()，所以任何5 極大一致集Γ 都滿足ΛB??(Γ)。因此，若Γ∈T(5)，即(Γ)?Γ，那么ΛB?Γ，即Γ∈B(5)。這說明了T(5)?B(5)。因此MCS(5)可以被完整地劃分為三個部分：T(5)、B(5)/T(5)以及B(5)。在這個基礎上，我們將5 的典范模型構造如下：

定義3(5 典范模型).定義5 的典范模型為CM5=(W，R，V)，其中

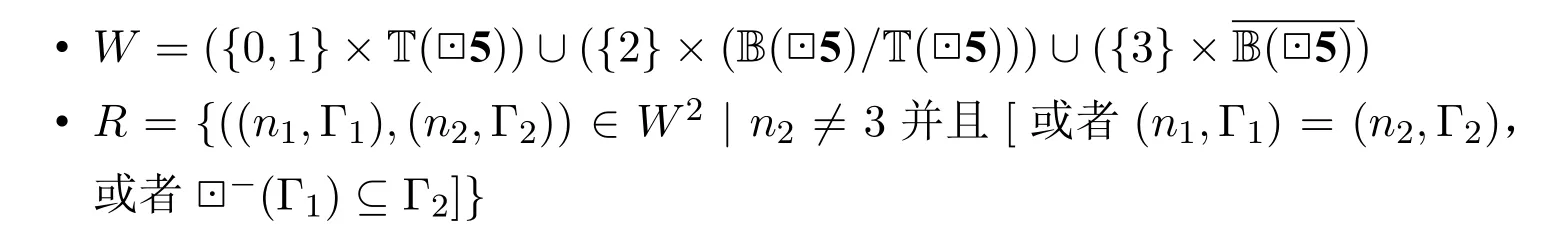
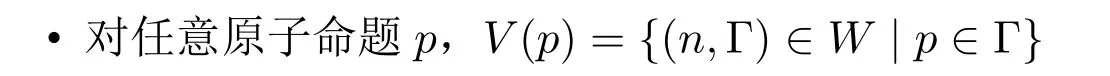
和自反典范模型的情形類似，對于CM5中的世界(n，Γ)，參數n規定了Γ的性質。當n ∈{0，1}時，，并且存在一個(n，Γ)的副本(1?n，Γ)；當n ∈{0，1，2}時，，并且(n，Γ) 可以連接到自身；當n=3 時，，并且(n，Γ)不會被任何世界連接到。

引理6(CM5的真值引理).對任何CM5中的世界(n，Γ)以及任意公式φ都有：

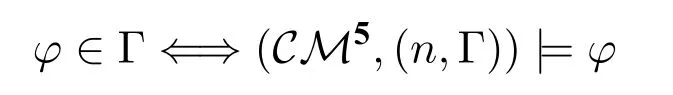
證明.我們對公式結構歸納，布爾情況易證，這里只考慮φ=的情況。

首先，當Γ 時，可知對任意(m，Γ′)∈W，若(n，Γ)R(m，Γ′)且(n，Γ)(m，Γ′)，則(Γ)?Γ′，因而α ∈Γ′，再由歸納假設，有(CM5，(m，Γ′))。因而由的真值條件可知(CM5，(n，Γ))。

其次，當/∈Γ 時，那么(Γ)∪{?α}一致，因此可以擴張為極大一致集Γ′，并且因為ΛB??(Γ)?Γ′，所以可知Γ′ ∈B(5)。進一步地，一方面，如果Γ′ ∈T(5)，那么令m=(n ?1)6?2n，易證此時無論n取何值，必然有且m ∈{0，1}，從而有(m，Γ′)∈W、(n，Γ)(m，Γ′)并且(n，Γ)R(m，Γ′)。另一方面，如果Γ′/∈T(5)，即(Γ′)?Γ′，又因為(Γ)?Γ′，所以ΓΓ′，此時令m=2，從而也有(m，Γ′)∈W、(n，Γ)(m，Γ′)并且(n，Γ)R(m，Γ′)。由歸納假設可知(CM5，(m，Γ′))α，從而由的真值條件可知(CM5，(n，Γ))。

引理7.CM5=(W，R，V)基于持續、歐性框架。

證明.首先證明CM5=(W，R，V)基于持續框架。令(n，Γ)∈W，考慮兩種情況：第一，當(Γ)是不一致的時，易證ΛB?Γ，因此Γ∈B(5)，從而可知。根據定義可知，此時有(n，Γ)R(n，Γ)。第二，當(Γ)是一致的時，那么它可以被擴充為極大一致集Γ′，并且因為ΛB??(Γ)?Γ′，所以Γ′ ∈B(5)；進一步地，如果Γ′ ∈T(5)則令m=0 否則的話令m=2，易證(m，Γ′)∈W并且(n，Γ)R(m，Γ)。

接著，我們證明CM5=(W，R，V)基于歐性框架。假設(n1，Γ1)R(n2，Γ2)并且(n1，Γ1)R(n3，Γ3)，我們以此證明(n2，Γ2)R(n3，Γ3)。首先注意，根據定義可知n2，n3∈{0，1，2}，這意味著Γ2，Γ3∈B(5)，即ΛB?Γ2且ΛB?Γ3。如果(n2，Γ2)=(n3，Γ3)，那么根據定義直接有(n2，Γ2)R(n3，Γ3)；如果(n3，Γ3)但Γ2=Γ3，那么必然有Γ2，Γ3∈T(5)，所以有(Γ2)?Γ2=Γ3，因而有(n2，Γ2)R(n3，Γ3)。因此，現在僅需考慮Γ2Γ3的情況。這時進一步分為三種情況討論：

由引理6 和引理7，以及命題4，我們得到了系統5 的完備性結果：

定理6(5 的完備性).系統5 相對于歐性框架類5以及持續歐性框架類D5都是可靠完全的。

4 雙模態邏輯：加入必然算子

第2 節指出在許多框架類上強可弱必邏輯語言SW和模態邏輯語言ML在表達力上不可比較，因此包含了必然算子和弱必然算子的雙模態語言ML+的表達力在許多框架上都嚴格強于SW和ML。9一個值得注意的事實是混合模態邏輯語言的表達力要比ML+ 更強，因為在混合模態邏輯語言中φ 和φ 可以分別被定義為↓i (?i →φ)和↓i (?i ∧φ)。本節將對ML+的公理系統作一個初步探究，因而所談論的公式也均指ML+公式。

首先，不難發現以下用于刻畫必然算子和弱必然算子之間關系的橋接公理是有效的：

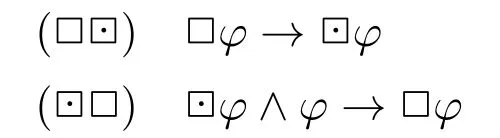
給定任意關于2的正規模態邏輯L，令，那么我們得到了一個同時刻畫必然性和弱必然性（以及可能性和強可能性）的邏輯。在很多情況下，L+作為L 的雙模態擴張都是恰當的。

定義4.給定關于的正規模態邏輯L，L+的典范模型被定義為CML+=(W，R，V)，其中

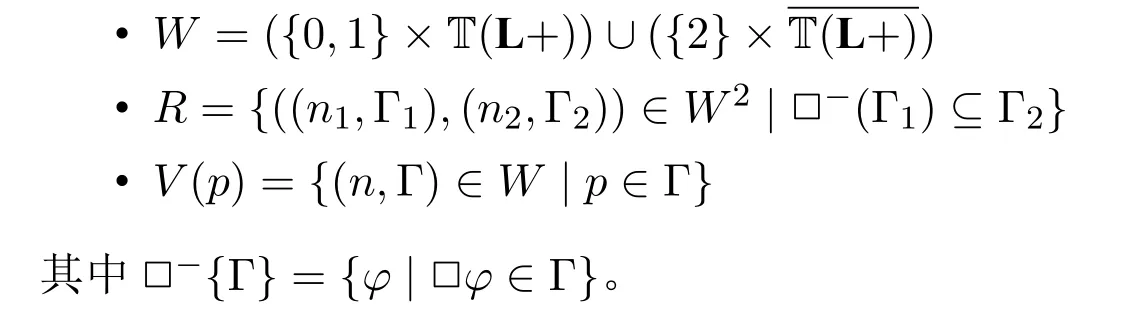
引理8(CML+的真值引理).給定關于的正規模態邏輯L，對于CML+=(W，R，V)中的任意世界(n，Γ)以及任意公式φ都有：

證明.我們只考慮φ=的情況。

首先，當Γ 時，那么考慮任意(m，Γ′)∈W滿足(n，Γ)(m，Γ′)且(n，Γ)R(m，Γ′)。一方面，如果α ∈Γ，那么因為公理() 有Γ，從而可得Γ，又由(n，Γ)R(m，Γ′)可得α ∈Γ′。另一方面，如果α/∈Γ，那么Γ/∈T(L+))，因而必然有ΓΓ′，因此存在β使得β ∈Γ但是?β ∈Γ′，由β ∈Γ 和Γ 易得(α ∨β)∧(α ∨β)∈Γ，又由公理()有(α ∨β)∧(α ∨β)(α ∨β)∈Γ，從而可得2(α ∨β)∈Γ，又因為(n，Γ)R(m，Γ′)，所以有α ∨β ∈Γ′。又因為?β ∈Γ′，所以α ∈Γ′。因此，無論如何都有α ∈Γ′。由歸納假設可得(CML+，(m，Γ′))。由的真值條件，可得(CML+，(n，Γ))。

其次，當/∈Γ 時，(Γ)∪{?α}一致，進而可擴充為極大一致集Γ′。由公理():可知(Γ)(Γ)，從而有(Γ)?Γ′。如果Γ=Γ′，那么可知Γ∈T(L+)，從而n ∈{0，1}，此時我們令m=1?n；如果ΓΓ′，那么如果Γ′ ∈T(L+)，我們令m=0，否則令m=2。在以上各種情況中都有(m，Γ′)∈W、(n，Γ)(m，Γ′)并且(n，Γ)R(m，Γ′)。由歸納假設可知，(CML+，(m，Γ′))α。由的真值條件，可得(CML+，(n，Γ))。

容易驗證，CMD+、CMT+、CM4+、CMB+、CM5+、CMS4+以及CMS5+分別基于持續框架、自反框架、傳遞框架、對稱框架、歐性框架、自反傳遞框架以及等價框架。因此，我們得到了如下的完備性結果：

定理7(雙模態系統的完備性).必然和弱必然的雙模態邏輯系統K+、D+、T+、4+、B+、5+、S4+以及S5+分別相對于全框架類、持續框架類、自反框架類、傳遞框架類、對稱框架類、歐性框架類、自反傳遞框架類以及等價框架類是可靠完全的。

一個自然的猜想是：對于任意框架類F，令LML(F)和LML+(F)分別是模態語言ML下和雙模態語言ML+下刻畫該框架類的邏輯，那么LML+(F)=LML(F)+。然而，這個猜想并不正確。考慮所謂的平庸框架類：在平庸框架上每個世界都有且僅有一個可及世界，即它自身。不難驗證，刻畫平庸框架類的單模態邏輯系統是Triv=K+(Triv):。在平庸框架中，每個世界都無法連接到除自己之外的其他世界，所以是平庸地有效的，因此刻畫平庸框架類的雙模態邏輯系統顯然是Triv=Triv+(Ver):。然而，系統Triv+和系統Triv 并不等價。

命題5.系統Triv+和系統Triv 不等價。

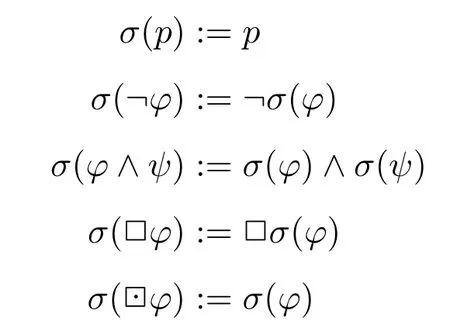
證明.令σ是一個從ML+公式到ML公式的翻譯函數，它被歸納定義為：通過對證明長度的歸納，不難驗證對于任何ML+公式φ，若Triv+φ，那么Triv+σ(φ)。因此，由于σ((p ∧?p))=(p ∧?p)并且Triv+p ∧?p，所以Triv+(p ∧?p)。但是因為Triv(p ∧?p)，所以系統Triv+和系統Triv不等價。

因此，通過給關于必然性的單模態邏輯添加橋接公理()和()，以得到相應的關于必然性和弱必然性的可靠完全的雙模態邏輯，這種方案并非永遠都是可行的。這是這兩個橋接公理在應用上的一個局限性。

盡管原來的猜想被證偽了，但這給我們提出了一個留待解決的新問題：

問題4.1.在何種充要條件下，框架類F滿足LML+(F)=LML(F)+？

5 結語

限于篇幅，本文主要對強可弱必邏輯的形式性質作了探究，未將之和他世界模態邏輯（即關于elsewhere，elsewhen 以及不等性的邏輯）、偶真性和本質性邏輯、偶然性及非偶然性邏輯等相關且重要的哲學邏輯作系統的比較研究，也未將之充分運用于哲學分析中。盡管如此，在以上的技術化工作中仍然隱含了許多哲學上有趣且重要的問題。比如說，在為強可弱必邏輯構建典范模型時，我們非常依賴于為可能世界建立“副本”的技巧。但是，既然這些互為“副本”的可能世界滿足了完全相同的命題，我們是依據何種理由將它們分辨為兩個不同的世界的？這個問題既是形而上學的，也是認識論的，但卻要留待以后再討論了。