三角函數的傅立葉變換推導公式

(大連理工大學 遼寧 大連 116023)

一、狄利克雷條件

設f(x)是以2l為周期并且定義在[-l,l]上可積。可以知道下列傅立葉級數的展開式：

(1)

然而想取等號時，需要公式(1)收斂，并且收斂于f(x)是需要條件的。其中最常見的是滿足狄利克雷條件。當f(x)滿足狄利克雷條件時，f(x)可以取等號，下列給出狄利克雷條件—函數f(x)在區間[-l,l]上滿足:

(1)連續，或只有有限個間斷點，且都是第一類間斷點；

(2)只有有限個極值點。

(2)

當函數滿足狄利克雷條件時，第一行為x∈(-l,l)在f(x)的連續點，第二行為x∈(-l,l)在f(x)的第一類間斷點，第三行為x=±l函數的端點值。

二、三角函數的傅立葉變換

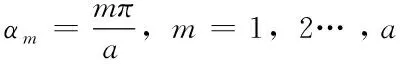
由于上述公式為非周期函數且取值范圍在[0,a]。根據上述傅立葉級數的描述情況，sin(αmx)滿足狄利克雷條件，所以我們把此三角函數進行偶延拓，再進行周期延拓，然后利用傅立葉級數進行表達：

(3)

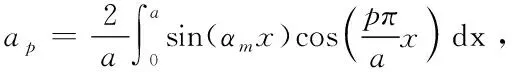
當m=p時，可以得到ap=0，所以下列為m≠p時：

將此過程置換順序之后，同理可得：

當p=0時：

根據上述得到的結論，可以把此三角函數寫成：

(4)

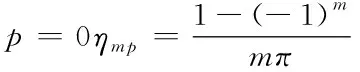
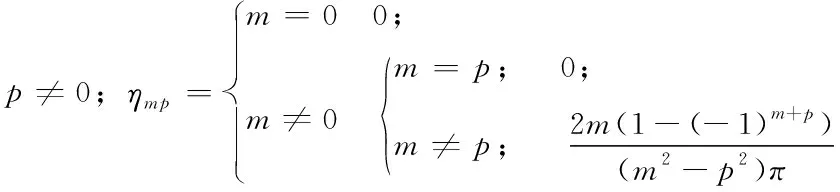
同樣，對于cos(αmx)也可以做上述推導，可以由讀者自行推導，驗證。本文簡單地介紹了傅立葉級數的使用和拓展，在純數學推導中研究傅立葉函數的應用。在我們無法進行理論證明的時候，采用直觀推斷的研究方法其實在早期的科學研究中，已經被廣泛地應用，因此也帶來了很多的重要發現，傅立葉級數就是其中之一。