MGF模型和SVM回歸法在甘河加格達奇站年最大流量長期預報中的應用
劉文斌 于成剛
(1.黑龍江省水文水資源中心,黑龍江 哈爾濱 150001;2.大興安嶺水文水資源中心,黑龍江 加格達奇 165000)
分析預測年最大流量的主要意義在于定量描述預測年份的洪水量級,為防洪決策提供支撐,但年最大流量的變化受江河前期底水,預見期內降水、蒸發、氣溫,水利工程、人類活動等諸多因素影響,具有很大不確定性。常用的時間系列分析技術和預測方法(如:多元線性回歸),對系列數據的極值和趨勢預測,不能體現年最大流量因受大氣環流變化而具有的與預報因子之間的非線性關系,存在精度不高的問題。現有的時間序列預測模型中,自回歸(AR)、自回歸滑動(ARMA)和門限自回歸(TAR)模型在進行多步預測時,預測值會趨于平均值,對極值的擬合效果欠佳。指數平滑模型和灰色模型等進行多步預測時,表示的是一種指數增長,不適用于預測起伏變化大的年最大流量。
針對時間系列預測模型對于轉折性變化預測能力較差的問題,依據氣候時間序列蘊涵不同時間尺度振蕩的特征,魏鳳英[1]拓展了數理統計中算術平均值的概念,定義了時間序列的均生函數,提出了視均生函數為原序列生成的、體現各種長度周期性的基函數的新構思。均生函數預測模型既可以作多步預測,又可較好地預測極值,為長期預報和短期氣候預測開辟了一條新途徑[3]。采用均生函數作多步預測,可以改善其他時間序列模型的不足,改善對序列極值的擬合與預測效果。
支持向量機(Support Vector Machines,SVM)以統計理論為基礎,能較好地解決小樣本、非線性、高維數和局部極小點等問題,是一種新穎有效的處理非線性分類和回歸的方法。本文即以均生函數構成的周期性函數,結合支持向量機方法建立了甘河的加格達奇站年最大流量預測模型,有機地結合兩種方法的優點,克服了傳統時間系列預測方法對極值模擬精度較低和長期預測中存在的趨勢性預測的問題。在加格達奇站年最大流量預測的應用結果顯示,本文建立的模型預測結果既實現了數量和趨勢同步預測,也實現了該年最大流量系列非線性變化的預測,大大提高了預報精度。
1 研究資料和方法
1.1 資料
甘河發源于大興安嶺東坡伊勒呼里阿侖山脈的南支英吉奇山,由西北流向東南,匯入嫩江干流,全長446km,流域面積19549km2,流域內森林覆蓋率高,沒有過多人為活動影響,下墊面條件變化不大。加格達奇水文站為甘河中游控制站,多年平均降水量531mm,年際變化大,年內分布主要集中在6—9月,該站洪水為典型山溪性洪水,暴漲暴落,漲水期間水位、流量變化劇烈。
本文所用的資料為加格達奇站1952—2019年共68年的年內最大流量序列資料。
1.2 均生函數模型
均生函數(Mean Generating Function,MGF)是時間序列均值生成函數的簡稱,是由時間序列按不同時間間隔計算均值,生成的一組周期函數[7],將此函數進行周期性延拓,即在定義域上延拓到整個數軸,可構造出均生函數延拓矩陣。魏鳳英[1]將均生函數的概念推廣到回歸分析中,給出相應的建模方案,使回歸模型的擬合效果更為理想。
利用加格達奇站年最大流量系列構造最大流量周期性均生函數,采用CSC[1]雙向評分準則,選擇最優因子,利用SVM的K-CV統計分析方法學習訓練樣本,通過逐漸改變參數的取值,獲取最佳的參數組合,而后建立回歸模型進行擬合。計算1952—2001年的擬合值。根據模型對2002—2019年最大流量進行預測,最后與2002—2019年實測資料進行對比分析。
設時間序列為X(t)(t=1,2,…,n),構造均生函數:
(1)
(2)
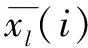
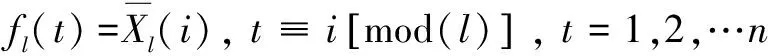
(mod表示同余)
(3)
F=(fij)n×m,fij=fl(t)
(4)
(5)
fl(t)為均生函數延拓序列,是一種周期性基函數。均生函數延拓矩陣中第1列記為f1,第2列記為f2,……,第m列記為fm。從f1、f2、…、fm中挑選出m個與原始序列密切相關的序列作為預報因子,建立模型進行模擬和預測。
1.3 支持向量機(SupportVector,SVM)回歸方法
支持向量機(SupportVector,SVM)是一種基于統計理論的算法,屬于有監督的學習方法,已知訓練點的類別,可學習求得訓練點和類別之間的對應關系,以便將訓練集按照類別分開,或者預測新的訓練點所對應的類別。
用線性回歸函數f(x)=ωx+b擬合數據{xi,yi},(i=1,2,…,n,xi∈Rd),yi∈R的問題,根據SVM理論,若采用線性ε不敏感損失函數
(6)
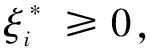
(7)
下,最小化目標函數
(8)
常數c>0控制對超出誤差ε的樣本的懲罰程度。采用優化方法可以得到其對偶問題,即在約束條件
(9)
(10)
從而得回歸模型
(11)
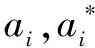
(12)
式(5)、(6)中的b*,取在邊界上的一點,即可確定。有關非線性核函數的種類較多,常用的有多項式核函數、徑向基核函數、柯西核函數等多種形式。本文采用徑向基核函數
K(x,xj)=exp(-(γ‖x-xi‖2),λ>0)(13)
1.4 年最大流量延拓均生函數
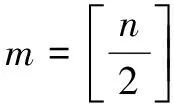
選取通過置信度0.01~0.05檢驗的函數因子作為預報因子。所選取的周期性基函數因子為5個。這5個周期性基函數分別為5年、11年、16年、18年、19年的函數,其中11年、18年的基函數因子通過了0.01的檢驗。這樣有效避免函數因子之間的復相關,確保各個因子間的獨立性。
2 周期檢驗和突變檢驗
2.1 周期檢驗
周期性檢驗采用小波分析法,該方法最早提出于20世紀80年代初,具有時-頻多分辨功能,能清晰地揭示出隱藏在時間序列中的多種變化周期。本文計算所用年最大流量系列包含“多時間尺度”變化特征且這種變化是連續的,所以選用連續復小波變換來分析該流量序列的多時間尺度特征,結果見圖1,結果顯示該系列存在11年、34年左右明顯的周期。
因此,加格達奇站流量隨時間出現周期性變化,具有一定起伏性,適合用MGF和SVM來解決極值預報的問題。
2.2 突變檢驗
流量系列的突變檢驗,采用滑動t檢驗(MMT)的方法。兩子系列長度n1=n2=11。給定顯著性水平a=0.01,t分布自由度ν=n1+n2-2=20,t0.01=±2.85,為了提高更嚴格的顯著水平,給定t0.01=±3.20。將計算出的t統計量序列和t0.01=±3.20繪成圖2。圖2顯示,流量系列自1952年以來,t統計量有一處超過0.01顯著水平,且為正值,說明年最大流量在20世紀70年代經歷了一次由大到小的突變。該次突變包含在過去的變化中,后期系列未出現突變,因此,可以依據率定的模型進行多步預測。
3 年最大流量預測模型
3.1 SVM回歸預測模型的建立
為了避免挑選出的周期性基函數因子之間的量級差異,消除各個因子由于量綱和單位不同造成的影響,首先對每個預報因子進行歸一化處理:
(14)
式中:xmax、xmin為原始數據x的最大值和最小值;ymax、ymin為映射范圍的參數,在這里取值為2和1。
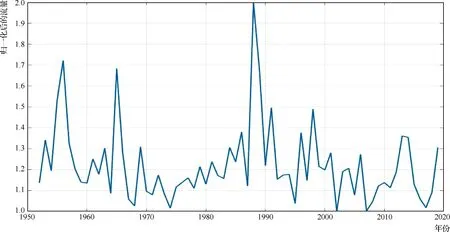
圖3 加格達奇站年最大流量歸一化后逐年數據曲線
建模時,將經過處理的預測因子(優選后的周期性基函數)作為輸入,年最大實測洪峰流量作為輸出,取前50年(1952—2001年)為檢驗樣本集,用于SVM進行學習訓練和驗證,后18年(2002—2019年)為預測檢驗樣本,歸一化后逐年數據曲線見圖3。選取線性ξ不敏感損失函數,采用徑向基核函數進行SVM建模,由于所選的參數值不同,函數形態會發生較大變化,進而引起SVM模型的變化。因此,在建模中利用K-CV[8]統計分析方法學習訓練樣本,通過逐漸改變參數的取值,以獲取最佳的參數組合,使建立的模型預測效果最好。經過多次交叉驗證學習和訓練,最終建立用于年最大洪峰流量預報的SVM回歸模型,經過計算其校正模型參數c為11.31,g為0.35,MSE為0.013。其參數計算結果見圖4、圖5。
3.2 SVM回歸模型預測效果分析
依據《水文情報預報規范》(GB/T 22482—2008)對中長期預報的精度評定的要求,流量數值預報誤差精度采用多年變幅的10%,而趨勢(定性)評分采用合格和不合格[4]。
SVM模型模擬和檢驗結果顯示:模擬和檢驗效果較好,精度較高,50個模擬數據符合誤差要求的共42個,合格率達84.0%;46個數據趨勢模擬正確,合格率達到92.0%。18個檢驗數據符合誤差要求的共13個,合格率為72.2%;14個數據趨勢模擬正確,合格率達到77.8%。極值的模擬結果較好,模擬數據的極值數據均符合誤差要求,預測值和實際觀測值對比曲線見圖6。
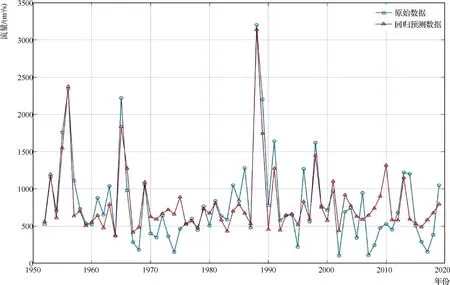
圖6 加格達奇年最大流量SVM預測值和實際觀測值對比曲線
3.3 逐步回歸預測模型
為了比較SVM回歸與逐步回歸方法的預測能力,本文同樣利用上述19個周期性基函數作為預報因子,選取不同F值引入不同的預報因子,采用逐步回歸方法建立加格達奇站年最大流量預測模型。依據模型的預測誤差最小原則,數學方程為
+0.547x19-1889.905
(15)
對檢驗樣本和預測樣本年最大流量數據進行了預測模擬,其回歸結果和實際觀測值對比見圖7。
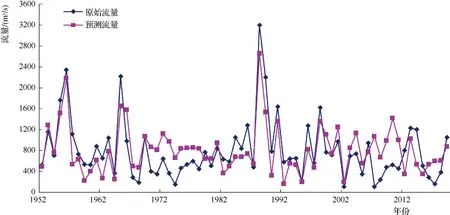
圖7 加格達奇站年最大洪峰流量多元逐步回歸預測值和實際觀測值對比曲線
3.4 逐步回歸模型預測效果分析
采用上述預報誤差精度進行評定,模擬和檢驗效果都不好,50個模擬數據符合誤差要求的共30個,合格率為60.0%;44個數據趨勢模擬正確,合格率達到88.0%。18個檢驗數據符合誤差要求的共10個,合格率為55.6%;9個數據趨勢模擬正確,合格率為50.0%。極值的模擬結果也不好,從圖7可以看出有2個極值的模擬數據差距都很大。
3.5 兩種模型對比分析結果
根據兩種方法的模擬結果,逐步回歸模型的數值預測合格率為60.0%,SVM回歸方法構建的模型合格率為84.0%,兩者相差達到24.0%。趨勢上逐步回歸模型合格率為88.0%,SVM方法構建的回歸模型合格率達到92.0%,兩者相差4.0%,但是逐步回歸在2個極值的模擬上都出現了較大差距,而SVM方法構建的回歸模型3個極值都模擬預測的很好。18年的檢驗結果中,逐步回歸模型的數值預測合格率為55.6%,趨勢模擬合格率為50.0%,而SVM回歸方法構建的模型合格率為72.2%;趨勢模擬合格率達到78.8%。
4 結 論
a.通過對加格達奇站年最大流量系列進行小波分析和滑動t檢驗,發現數據系列存在11年、34年左右周期,而在20世紀70年代存在一個由高到低的突變,說明該系列存在著明顯的非線性變化。按常規長期預報方法需提取周期、濾波趨勢,以及構建隨機過程的模型來進行外延預報。但如前文所述,常規預報方法并不能較好處理非線性數據系列,對極值和趨勢變化的預測能力尚有改善空間。本文即采用均生函數(MGF)、支持向量機(SVM)相組合的方法來提高預測能力。分析預報結果顯示,無論是極值還是趨勢預報,合格率均較高。
b.采用均生函數 (MGF)構建時間序列的周期性基函數,并對均生矩陣進行周期外延得到延拓矩陣,有效地實現了對時間系列數據的重構,一定程度上避免了單數據系列對預報結果的負面影響;而因子選取上采用CSC雙評分準則,提高了模型在數據趨勢預測上的能力,從而實現了數量和趨勢的雙預測。
c.運用SVM方法中的K-CV統計分析方法學習訓練樣本并優化參數。經過多次交叉驗證學習和訓練,最終計算其校正模型參數c為1,g為0.353,MSE為0.0081。交叉驗證提高了SVM類別識別最優參數集,間接提高了SVM回歸模型的精度。
d.通過均生函數(MGF)生成30個周期性基函數,采用CSC雙評分準則,篩選部分周期性基函數作為預測對象的影響因子,運用SVM中的K-CV統計分析方法學習訓練樣本、優化參數,最終建立年最大流量預測模型。模型預測結果顯示,無論模擬還是檢驗,本文所構建的模型均表現出明顯優勢,尤其在趨勢和極值的預測上克服了AR、ARMA等時間預測模型的極值均值化的問題。
e.對比采用均生函數(MGF)、多元逐步回歸相組合傳統預測方法,本文所構建模型的預測結果無論是極值還是趨勢預測都遠遠優于傳統預測方法,尤其在系列極值的預測能力上表現更為明顯。結果表明,新構建模型在處理年最大流量非線性變化方面有一定程度的改善。
根據目前水文行業開展年最大流量預報的實際情況,傳統中長期預報方法存在細節處理不細致、預測精度有待提高等問題,尤其針對極端洪水或干旱年份,極值預報誤差較大。本文主要針對數據系列的非線性變化和存在極值問題,利用均生函數(MGF)并結合支持向量機(SVM)構建年最大流量預測模型。通過在甘河加格達奇站的實際應用并與逐步回歸預測方法對比,本文所構建模型在模擬和檢驗中的預報結果均呈現明顯優勢,應用于工作實際是可行的。從水文領域的應用來看,該模型不僅提高了年最大流量非線性及極值預報能力,也實現了數量和趨勢雙預報,可更好應用于中長期預報。

