線性規劃布局模型在葡萄種植中的應用

李強 雷曉軍 虎良榮 阮蘭倉

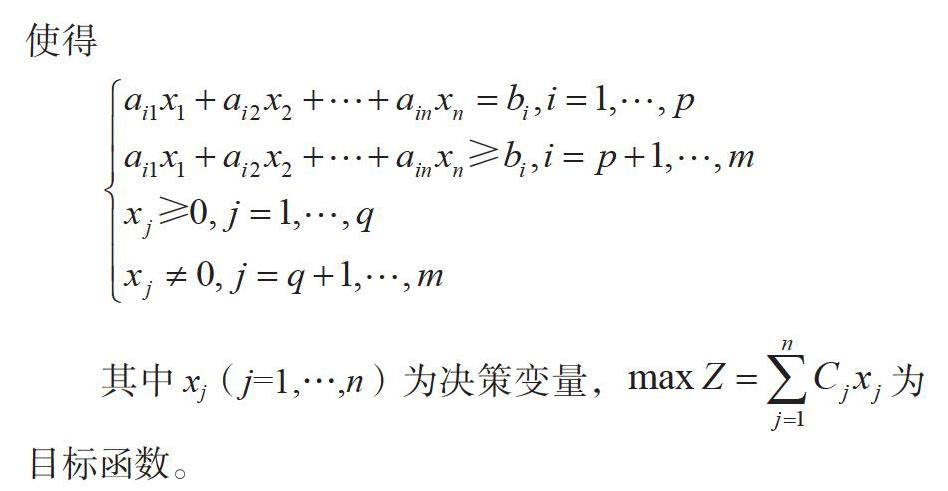
摘 要 現代農業規模化種植中，在條件不變的情況下，統籌安排、合理布局是使總的經濟效果達到最佳的科學方式，是提高農業產量的有效方法之一。基于此，結合貴州省銅仁市現階段農業現狀及銅仁市川硐鎮烏泥村葡萄種植情況，運用線性規劃就如何布局使其葡萄產量最佳進行分析，并給出葡萄種植的一般布局模型、解法及應用推廣示例。

關鍵詞 線性規劃;布局模型;農業;葡萄種植;合理布局

中圖分類號：F22 文獻標志碼：B DOI：10.19415/j.cnki.1673-890x.2020.09.090

在社會生產活動中，運用數學分析方法是提高經濟效果的科學方式。進入21世紀，隨著應用數學的高速發展，數學分析方法的運用在農業種植中的作用越來越明顯。特別是在規模化種植越來越普遍的現代農業種植中更具有不可或缺的作用。曾有過一系列關于線性規劃在經濟中應用的理論成果[1]。

在研究規模化種植業的活動中，因地制宜、合理布局、確定各種品種及不同作物在土壤上的種植面積，完成種植計劃的同時，使總產量達到最大是現代農業生產的基本要求，也是規模化種植業所面臨的巨大挑戰。基于此，結合銅仁市烏泥村葡萄種植的實際情況，就規模化葡萄種植布局進行分析。

1 銅仁市農業生產發展概況

基于黨和政府制定的一系列惠農政策，我國農業呈現出全面、穩定、協調發展的良好態勢。但與發達國家和現代農業發展的要求相比，我國農業生產發展的水平依然較低，生產組織化程度及規模化程度不夠。調整農業生產結構，使產業布局不斷優化，全面提高農村農業規模化、高度現代化是我國農業發展的必然趨勢[2]。

隨著新農村建設的推進，銅仁市新農村試點建設取得了一系列成就。但就總體而言，依然面臨以下3個方面的問題：1）外來商收購農特產品時，只有特色沒有數量和質量;2）本地農戶不敢大量種植，擔心銷路;3）種植碎片化，規模化不夠。加強科技下鄉，支持銅仁市“三農”事業發展，是改變這種現狀行之有效的手段之一，也是實現銅仁市農業現代化發展的基本要求[3]。

2 預備知識

線性規劃一般形式[4-5]為maxZ=C1x1+C2x2+…+Cnxn，使得

其中xj（j=1，…，n）為決策變量，為目標函數。

線性規劃模型的常見解法有單純形法、圖解法、兩階段法以及對偶單純形法[6-7]。

線性規劃問題解的基本性質：1）所有可行解構成的集合稱為可行域;2）如果集合k中任意兩點s、t之間連線上的點都是集合k中的點，即對于任意的s、t∈k，都有θS+（1-θ）t∈K（0≤θ≤1），則稱k為凸集;3）設k是凸集，x∈K，若x不能用不同的兩點x1∈k和x2∈k線性表示成x=θx1+（1-θ）x2（0≤θ≤1），則稱x是k的一個頂點（或極點）;4）線性規劃問題的基本可行解對應于可行域的頂點。

為了敘述討論的方便，作出如下規定：1）任何一編號區域內的土壤成分相同;2）同一種作物的不同品種均視為不同品種的作物;3）播種面積不得大于土地面積，且作物的種植面積非負。

對模型作如下2點說明：1）所有討論均是在光照、管理、水分等其他條件不變的情況下，即研究相同成分的土壤對不同品種作物的生長情況;2）所涉及數據均來自農民口中，所涉及數據可靠性較低。

3 布局模型及應用

3.1 種植布局模型

為了改變銅仁地區葡萄種植面臨的問題，擴大種植規模，進行如下的布局討論。一般地，假設將要在B1，B2，…，Bn這n塊土地上種植m中不同品種的葡萄A1，A2，…，Am。根據多年來的經驗，可知各葡萄在各土地上的產量。據此作出葡萄種植計劃如表1所示（產量單位：kg·hm-2）。

表1中：ai表示葡萄Ai今后的計劃種植面積（i=1，2，…，m）;bj表示土地Bj的作物種植公頃數（j=1，2，…，n）;Cij表示在土地Bj上種植葡萄Ai的產量（i=1，2，…，m，j=1，2，…，n）。

用線性規劃的方法來研究這一實際問題，根據規定，計劃播種總的面積不得大于土地的實際面積，即需滿足公式1。

假設xij（i=1，2，…，m，j=1，2，…，n）為土地Bj上種植葡萄Ai的公頃數，在各塊土地上種植葡萄Ai的公頃數應小于等于Ai的計劃播種公頃數，即應滿足公式2。

又因為種植面積不大于土地原有面積，即在土地Bj上種植各葡萄的公頃數應小于等于Bj的面積，于是有公式3。

其中，xij應滿足公式4。

于是，在滿足公式1～4的情況下，求一變量xij（i=1，2，…，m，j=1，2，…，n）的值，使達到最大值，這樣就可以得到一個關于線性規劃的布局模型，使得：

在這里，記模型Ⅰ的約束系數的約束矩陣為A，右端向量為b。其中，

由于，在結合實際種植時，應盡量利用土地這一客觀事實。可以證明，A的秩至多為m+n-1，因此A至多有m+n-1個線性無關的列。因此，布局模型Ⅰ的任意一個基本解都至多有m+n-1個基變量。這m+n-1個基變量對應的值就是一種葡萄的種植方案，在眾多方案（即眾多解）中一定存在一個最優解，在滿足種植計劃的前提下，使總的產量最多。而求出這個最優解，就是對應的合理布局。

3.2 最優布局模型的解法

考慮實際種植情況，不妨設種植模型Ⅰ的可行區域D={x∈Rn|Ax=d，x≥0}，其中A為模型Ⅰ的約束系數的約束矩陣，b為右端向量，x為一個滿足所有約束條件的向量[8-9]。其中，x=（x11，…，x1n，x21，…，xmn）T，b=（a1，…，am，b1，…，bn）T，

有以下3條定理。

1）種植模型的可行區域D={x∈Rn|Ax=d，x≥0}是凸集。證明：?x，y∈D，有W=θx+（1-θ）y，其中θ∈[0，1]，又x≥0，y≥0，Ax=d，Ay=d，故AW=θAx+

（1-θ）Ay=d，即W∈D。

2）種植模型可行域中的頂點是有限的，而這些頂點就是對應的種植模型的基本可行解。

3）種植模型的基本可行解是有限的，且有限的基本可行解中至多有有限個最優解。

事實上，由組合的知識可知，在n塊不同土地上種植m種不同的葡萄，可確定不超過（nm）種不同的方法;另一方面，可以根據種植計劃把現有土地分成與種植計劃相同的塊數，在實際中，這種方法是有限的。

結合定理1、2，可以知道種植模型一定存在一個基本可行解是最優解，而這個最優解就對應一種最佳的布局方案。可以用常見的線性規劃解法及數學軟件Lingo來求布局模型的最優解。

3.3 葡萄種植應用舉例

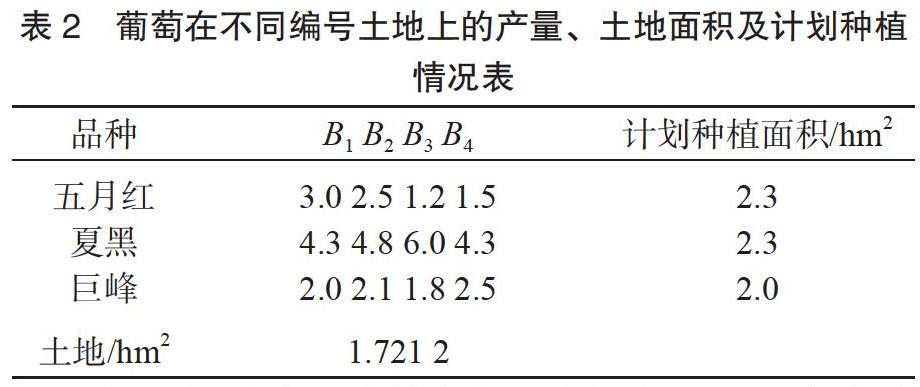
為了說明布局模型Ⅰ的合理性及可行性，結合銅仁市川硐鎮烏泥村葡萄種植情況，運用模擬數學實驗的方法來進行布局淺析。1）在烏泥村選取4塊土壤成分不同的土地各100 hm2，而每一塊土地的土壤對同一種葡萄的生長影響一致，設這4塊土地分別為B1、B2、B3、B4。2）選定五月紅、夏黑、巨峰3中優良葡萄進行種植。結合以往葡萄種植經驗，不同葡萄在不同編號土地上的單位產量、土地面積及計劃種植情況見表2。

為了討論方便，并結合實際種植時的需要，假定計劃種植面積與土地實際面積相等。

令xij（i=1，2，3，j=1，2，3，4）分別為五月紅、夏黑、巨峰在B1、B2、B3、B4這4塊土地上的種植面積，并用Z來表示3種葡萄的總產量。由模型Ⅰ可知，在完成種植計劃的前提下，總產量最大，即說明布局合理。于是，有以下結果。maxZ=3x11+2.5x12+1.2x13+1.5x14+4.3x21+4.8x22+6x23+4.3x24+2x31+2.1x32+1.8x33+2.5x34

使用Lingo來求解布局模型Ⅱ，解得x11=1.7，x12=0.7，x22=1.3，x23=1，x34=2，Z=24 067。

于是，得到一組變量x=（1.7，0.7，0，0，0，1.3，1，0，0，0，0，2），

表示在編號為B1的土地上種1.7 hm2五月紅，在編號為B2的土地上種0.7 hm2五月紅，在編號B2的土地上種1.3 hm2

夏黑，在編號B4的土地上種2.0 hm2巨峰為最佳的布局方案。此時，在往年其他情況（如管理、光照、水分等）不變條件下，葡萄總的產量預計為315 500 kg。于是得到最優布局如表3所示。

考慮葡萄種植的長期性，將編號為B2的土地分成B21和B22兩塊。其中，B21=0.7 hm2，B22=1.3 hm2，于是，就得到所要的最佳布局方案及預期產量表4。

4 布局的推廣

結合實際不難發現，該模型在水果、農產品和蔬菜等種植中均有重要的作用，如在蔬菜大棚種植蔬菜時可根據市場需求量及土壤情況，選擇最佳的土壤來種植。同時也可為制定銅仁地區未來農業發展方向提供參考。

5 結論

隨著科學技術的不斷發展，未來農業一定會走向規模化發展的道路，葡萄種植也是如此，而科學合理的布局是未來農業發展的有力武器。筆者在實際考察的基礎上給出了不同土壤中不同作物生長情況的一般布局模型，并進行了簡單的應用舉例和應用方向的推廣，促進了葡萄規模化種植中線性規劃布局模型的應用。

參考文獻：

[1] 雷曉軍，梁治安.證券組合投資模型優化[J].商場現代化，2007（24）：171-172.

[2] 付海蘭，雷曉軍.網絡環境下職業技術教育立體化教學的構建與實踐[J].中國大學教學，2011（8）：39-41.

[3] 張勇.新農村建設長效機制探索——對銅仁地區新農村建設的社會人類學調查及思考（上）[J].銅仁學院學報，2008，10（3）：54-58.

[4] 刁在筠，劉桂真.運籌學[M].北京：高等教育出版，2007.

[5] 《現代應用數學手冊》編委會.運籌學與最優化理論卷[M].北京：清華大學出版社，2001.

[6] Winston W L.運籌學概率模型應用范例與解法[M].北京：清華大學出版社，2006.

[7] 孔祥智.2009中國“三農”前景報告[M].北京：中國時代經濟出版社，2009.

[8] 焦寶聰，陳蘭芝.運籌學的思想方法及應用[M].北京：北京大學出版社，2008.

[9] 邢文訓，謝金星.現代優化計算方法[M].北京：清華大學出版社，2001.

（責任編輯：趙中正）

收稿日期：2020-02-15

作者簡介：李強（1977—），男，貴州松桃人，碩士，副教授，研究方向為數學教育與數學建模。

為通信作者，E-mail： 1132129812@qq.com。