偏心率對CFRP鋼管約束混凝土柱力學性能的影響

李 文，谷長霖，梅寶瑞

(東北石油大學，黑龍江 大慶 163318)

鋼管混凝土結構是用鋼管包裹混凝土的一種組合結構，從力學性能上看，混凝土與鋼管一起承壓可以充分發揮混凝土的受壓性能和鋼管的受拉性能，鋼管約束混凝土不但提高了混凝土的抗壓強度，也提高了其塑性變形能力和韌性性能。另一方面鋼管也可以充當施工模板，節省模板費用。纖維增強復合材料(Fiber Reinforced Polymer, FRP)[1-2]具有自重輕、抗拉強度高、抗疲勞性能優良等特點，隨著碳纖維復合材料[3-10]在工程領域越來越多的應用，該結構形式的纖維材料約束鋼管混凝土組合柱的探索與研究也成為了一項重要課題。

目前，有關FRP應用于加固方面的研究較多[11-14]，但有關將FRP與鋼管組合為復合管約束混凝土的相關研究相對較少。同時，在實際工程中的構件柱通常受軸力和彎矩的共同作用，故可以等效為一個偏心的軸向力，因此研究偏心率對構件的影響顯得尤為重要。本文研究CFRP鋼管約束混凝土柱力學性能，分析偏心率對CFRP鋼管約束混凝土柱的影響規律，為實際工程應用提供理論依據。

1 有限元模型

1.1 有限元模型的建立

CFRP為各向異性材料，其在達到極限拉應變之前定義為理想線彈性材料，當超過極限拉應變時材料發生破壞，承載力下降為0。根據簡化計算需要，鋼材采用的是雙線性隨動強化模型，屈服準則采用Von Mises屈服準則[15-16]。混凝土采用塑性損傷模型。

混凝土定義為八節點縮減積分格式的三維實體單元C3D8R，鋼管定義為殼單元S4，CFRP布定義為膜單元M3D4[17]。端板定義為三維實體單元，其厚度為20 mm。網格的密度劃分對試驗結果有一定的影響，經過不斷調整網格大小，取兩次分析結果相差較小的網格大小，對組合柱和剛性端頭進行網格劃分，設置全局單元尺寸為0.1。劃分網格后的CFRP與核心混凝土部分(圖1)。

圖1 網格劃分Fig.1 The diagram of gridding

本文借鑒文獻[18]的方法，在柱上下底面分別施加兩個剛性墊板，在兩端剛性墊塊上創建兩個偏心參考點，通過施加位移荷載來施加偏心荷載，將參考點與剛性墊塊進行耦合，對柱頂參考點約束X、Y方向位移，在參考點上施加Z方向位移荷載，對柱底參考點約束X、Y、Z三個方向位移(鉸接)，如圖2所示。

圖2 邊界條件Fig.2 The diagram of the boundary conditions

1.2 試件設計參數

根據相關規定，本文鋼管厚度取6 mm，鋼管外徑取500 mm，柱高取800 mm；采用一層加固CFRP布，其具體參數如下：理論厚度為0.167 mm，彈性模量為2.3×105N/mm2，密度為1.8 g/cm3，泊松比為0.17。

兩組長細比分別為22.4、28。A組及B組偏心率都分別為0.3、0.6、0.9、1.2。鋼管材料性能參數及所需模擬的試件參數見表1和表2。

表1 鋼材性能

表2 構件分組

1.3 模型驗證

將參考文獻[7]試驗數據與有限元模擬結果對比，表3給出了試件在ABAQUS計算所得承載力與試驗所得承載力，可以看出模擬極限承載力與試驗承載力比值介于0.83～1.04之間，平均值為0.96，均方差為0.06，誤差在可接受的范圍內，說明模擬與試驗結果比較吻合，因此可進行接下來的模擬運算工作。

表3 模擬對比驗證數據

2 有限元分析結果

2.1 不同偏心率作用下構件的等效應力云圖分析

圖3為不同偏心率作用下極限承載力下各部件的應力云圖。環向CFRP的最大等效應力均達到極限強度1 265 MPa，隨著偏心距的增大，達到極限應力的區域向柱中區域縮小，環向CFRP的緊箍力減小。鋼管均達到了屈服強度，鋼管的等效應力轉變為向柱中距荷載較遠一側擴大，柱中兩側最大應力分布相差越來越小。主要原因是偏心率較小時，柱子距荷載較遠一側因彎矩產生的拉力較小，當偏心率增大時，相同荷載產生的彎矩增大，對鋼管另一側的拉應力也相應增大。對于混凝土區域，當偏心率為0.3、0.6、0.9、1.2時，最大壓應力值分別為88.2、75.9、72.0、70.3 MPa，最大拉應力值分別為32.5、41.7、45.5、43.1 MPa，可以看出最大壓應力值隨著偏心率增高而降低。最大拉應力在偏心率0.3～0.9之間隨著偏心率增大而增大，在偏心率0.9～1.2之間略有下降。隨著偏心率的增大，受拉區域相對于受壓區域有所增大。

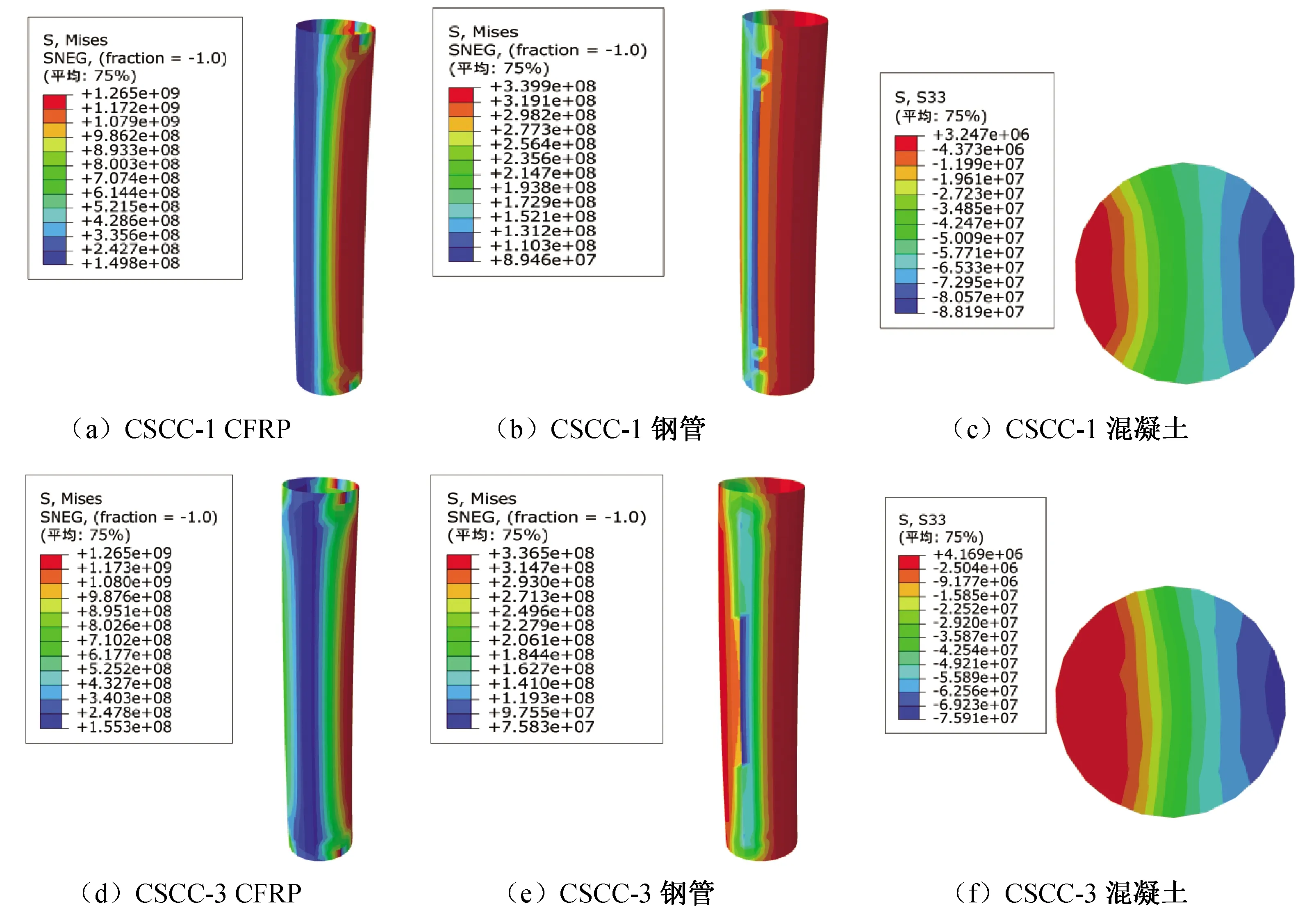
圖3 不同偏心率下試件應力云圖Fig.3 The diagram of stress nephograms of specimens with different eccentricity

偏壓柱到達極限承載力時，截面上出現不同程度的塑性變形，隨著偏心距的增大受壓區減小，壓區塑性應變也相應變小，塑性變形變小，導致被動約束緊箍力也就減小，即隨著偏心距的增大，被動約束的緊箍力減小。由于橫截面受壓區應力越靠近受壓側邊緣應力值越大，塑性變形越大，因此對于同一截面上的緊箍力是不均勻的。

2.2 荷載-撓度曲線

荷載-撓度曲線如圖4所示，可以看出偏心率對柱的荷載-撓度曲線形狀有較大的影響，偏心率大的構件極限力較小，上升段整體斜率及極限承載力對應的撓度較小，即剛度較小。如圖4(a)所示，在長細比為22.4，偏心率為0.3時，隨著極限承載力的增加，撓度呈近似線性變化，當極限承載力達到9 900.87 kN時，曲線呈下降趨勢；當長細比為22.4，偏心率為0.6，極限承載力僅達到6 341.55 kN時，曲線即開始下降。當長細比一定時，隨著偏心率的增加，荷載-撓度曲線整體呈下降的趨勢。主要原因是隨著偏心率增加，截面的受拉區及受壓區應力分布發生了改變，受拉區相對受壓區增大，在較小的荷載下受拉區混凝土就已經開裂，導致其極限承載力降低。

2.3 極限承載力對比

由表4可知偏心率對極限承載力有較大的影響，A組試件CSCC-3比CSCC-1降低了35.9%，CSCC-5比CSCC-3降低了32.7%，CSCC-7比CSCC-5降低了27.7%；對比B組數據的極限承載力有著同樣的降低趨勢，可知隨著偏心率的增大柱的承載力降低，且降低幅度減小；偏心率對不同長細比的構件影響不同，長細比為28時，試件的承載力相應地整體降低。

圖4 不同偏心率下荷載-撓度曲線Fig.4 The diagram of load-deflection curves at different eccentricity

試件組名試件名稱長細比λ鋼管約束效應系數ξs偏心率eCFRP約束效應系數ξcf混凝土強度極限承載力N/kN極限承載力提高幅度/%ACSCC-122.40.590.30.07C409 900.87-CSCC-322.40.590.60.07C406 341.55-35.9CSCC-522.40.590.90.07C404 270.61-32.7CSCC-722.40.591.20.07C403 088.26-27.7BCSCC-2280.590.30.07C408 841.7-CSCC-4280.590.60.07C405 735.57-35.1CSCC-6280.590.90.07C403 978.47-30.6CSCC-8280.591.20.07C402 892.53-27.3

根據圖5可以看出隨著偏心率的增大，曲線斜率的絕對值逐漸減小，即隨著偏心率的增大，極限承載力的降低幅度變小。

圖5 偏心率e-極限承載力N關系曲線Fig.5 The diagram of eccentricity e-ultimate bearing capacity N relation curve

3 結論

1)隨著偏心率的增大，受壓區減小，壓應力整體減小，其受壓區塑性應變也就越小，導致被動約束緊箍力也就減小，即隨著偏心率的增大緊箍力減小。

2)由于截面受壓區應力越靠近受壓側邊緣應力值越大，塑性變形越大，緊箍力在同一個截面上是不均勻的。

3)隨著偏心率的增大，受拉區域相對于受壓區域有所增大，構件的極限承載力降低，且降低幅度減小，偏心率與極限承載力呈非線性關系。

4)極限承載力隨著長細比的增大而整體減小。