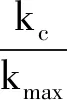常用的邊坡地震位移簡化算法對比

李存興，莫建新，王 成

(中交第二航務工程勘察設計院有限公司，湖北 武漢 430060)

近幾年來，伴隨著國家“一帶一路”倡議的拓展，我國工程建設企業在國際工程領域的影響力逐步擴大，進而參與建設的項目也逐漸增多。然而，不少工程位于環太平洋地震帶或歐亞地震帶，地震烈度高，水工結構抗震設計成為工程設計的重中之重。

斜坡式護岸作為圍海造地項目常見的結構形式，其合理的抗震設計將有利于節約工程總投資。國內規范對斜坡式護岸地震作用下穩定性分析采用的方法是擬靜力法，但擬靜力法只提供一個安全系數，不能反映邊坡最終變形情況。當安全系數小于1.0時，國際通用規范均允許采用位移法評價護岸工程在地震作用下的安全性。美國土木工程師協會和海岸、海洋、港口及內河研究所聯合發布的碼頭抗震設計規范ASCE/COPRI61-14[1]，國際航運協會的抗震設計規范PIANC WG34[2]，英國建筑工業研究與情報協會、美國陸軍工程兵團和法國生態可持續發展和能源部等聯合發布的國際堤防工程手冊USACE&CIRIA C731[3]等都明確規定：當安全系數小于規定時，可以通過計算堤體位移來評估結構的安全性，比傳統擬靜力分析更能反映結構的破壞程度。

本文結合工程實例，介紹了幾種邊坡地震位移簡化計算方法，分別選取臨界地震系數、峰值地震系數、峰值速度、地震震級、結構周期、地震反應譜或阿里亞斯烈度等指標獲取最終的邊坡永久位移，并基于美國地質地震局SLAMMER程序的SLIDE2018軟件位移分析進行對比。

1 地震位移簡化計算

1.1 理論簡介

Newmark滑塊位移法[4]最初由Newmark于1965年提出，用于岸坡和土石壩的永久變形計算。半個世紀以來，經過眾多研究者不斷探索和實踐，這種計算方法和模型在理論和工程應用等方面都得到極大的發展。如圖1所示的剛塑性滑塊模型，滑塊代表具有任意形狀滑動面的潛在滑動量，a(t)為地震波加速度時程。最初的Newmark滑塊位移法假定，坡體的地震荷載可以用一個擬靜力荷載代替，擬靜力荷載為擬靜力地震系數k與潛在滑動體重力的乘積，地震中岸坡破壞會形成明顯的滑動面，當地震荷載超過滑動體的極限承載力時，滑動體會沿著潛在的滑動面產生塑性位移。

假定屈服加速度(臨界加速度)在整個地震歷時中保持恒定(地震過程中土體強度不會發生明顯退化)。當施加在滑塊上的地震加速度超過屈服加速度(岸坡擬靜力穩定安全系數為1時的加速度)時，即t1時刻滑塊位移發生，滑塊的速度可以通過對陰影部分積分得到，滑塊的速度會一直增加到t2時刻，此時加速度再次降到屈服加速度以下，并且隨著加速度反向，速度最終在t3時刻減為零，滑塊位移可以通過對速度時間的關系進行積分得到。由圖1可知，滑塊位移的大小取決于施加加速度的幅值(地震動振幅)、單次歷時時間(頻率)和在整個地震歷時中加速度超過屈服加速度的次數(持時)。

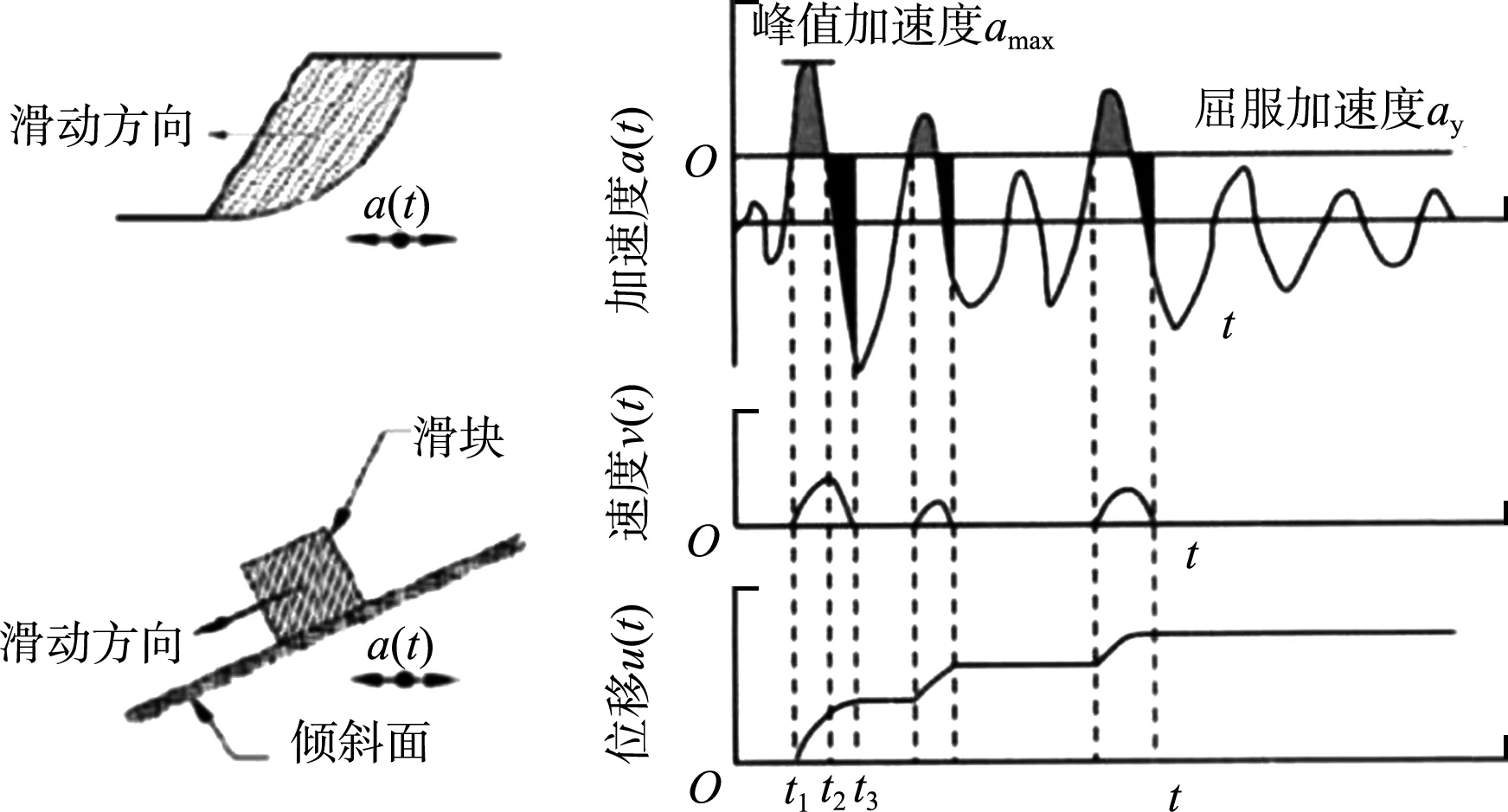
圖1 Newmark算法原理

1.2 地震位移簡化計算公式

近年來，國外諸多學者和行業協會通過對地震數據進行收集、分析和研究，基于Newmark滑塊位移概念，總結得出了多種典型的地震下永久位移的簡化經驗計算公式。經過歸納分析，根據考慮要素的不同，可以分為6大類。

1.2.1考慮臨界加速度和峰值加速度

Ambraseys & Menu[5]分析11次地震的50個強震記錄，提出了各種再回歸方程估算Newmark位移作為臨界加速度的函數，并根據研究結果提出了位移計算公式：

(1)

式中:DN為地震下永久位移；kmax為峰值地震系數，即地震峰值加速度amax與重力加速度g的比值；kc為臨界地震系數，即臨界加速度ac與重力加速度g的比值，可以通過試算確定或軟件工具求得。

1.2.2考慮臨界加速度、峰值加速度和地震震級

Jibson[6]對1994年美國加州Northridge市地震誘發的滑坡事故建模計算進行危險性評估，考慮到地震震級的影響，得出了一個適用于震級在[5.3, 7.6]范圍的位移計算公式：

0.424Mw±0.454

(2)

式中：Mw為地震震級。

1.2.3考慮峰值速度、峰值加速度和臨界加速度

美國公路合作研究組織的《擋土墻，埋入式結構，斜坡和堤防的抗震分析與設計手冊》NCHRP 611[7]對地震數據進行相關性分析，給出了永久位移與峰值速度、臨界地震系數、峰值地震系數的關系，常用的計算公式為：

lgDN=-1.51-0.74lg(kC/kmax)+3.27lg(1-kC/kmax)-

0.80lgkmax+1.59lg(PGV)

(3)

式中：PGV為地震峰值速度(以英寸計)。

美國聯邦公路局國家公路研究所出版的《交通工程巖土特性與結構地基抗震設計參考手冊》(FHWA-NHI-11-032)[8]也采用上述公式。

1.2.4考慮滑動體基本周期、地震反應譜、臨界加速度和地震震級

Bray & Travasarou[9]通過收集大量的地震資料，運用非線性耦合黏滑塊模型，采用概率方法分析地質穩定性，得出了不同條件下非零位移的計算公式：

lnDN=-1.10-2.83lnkc-0.333(lnkc)2+0.566lnkc·

ln[Sa(1.5Ts)]+3.04ln[Sa(1.5Ts)]-0.244·

ln[Sa(1.5Ts)]2+1.5Ts+0.278(Mw-7)±ε

(4)

式中：Ts為滑動體基本周期，按照圖2模式計算；Sa(1.5Ts)為1.5倍基本周期Ts對應的地震加速度反應譜；ε一般取0，正負偏差0.66。

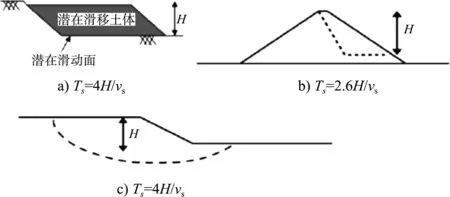
注：對于滑坡體高度大于邊坡高度的情況，Ts=4H/vs，其中H為滑動體高度，vs為滑坡區域土體的剪切波速。

圖2潛在滑動體的基本周期計算模式

1.2.5考慮滑坡體高度、坡頂峰值加速度、臨界加速度和地震震級

Makdisi & Seed[10]在Newmark模型的基礎上進行了改進，采用等效線性模型計算潛在的滑動體平均地震反應。利用靜力分析得到相關計算參數，從而近似評估岸坡在地震作用下的永久位移。基本步驟歸納如下：

1)根據地震峰值基底加速度PBA(peak base acceleration)查圖3a)求得坡頂峰值加速度PCA(peak crest acceleration),為方便對比計算，根據曲線擬合了兩者關系:

(5)

2)根據滑弧高度與堤身高度的比值，查圖3b)求得滑塊的平均加速度。由于滑弧高度大于堤身高度，按照y/h=1.0對應的上限求得滑塊的平均加速度u0max= 0.47PCA。滑動體的平均最大地震系數k0max=u0max/g。

3)求得滑塊滑動臨界地震系數kc。

4)計算臨界地震系數與平均最大地震系數的比值：

λ=kc/k0max

(6)

5)計算滑坡體結構周期Ts。

6)查圖4求得滑體位移，圖4a)為位移范圍，4b)為位移中值。為方便對比計算，對圖4b)數據進行了曲線擬合分析。

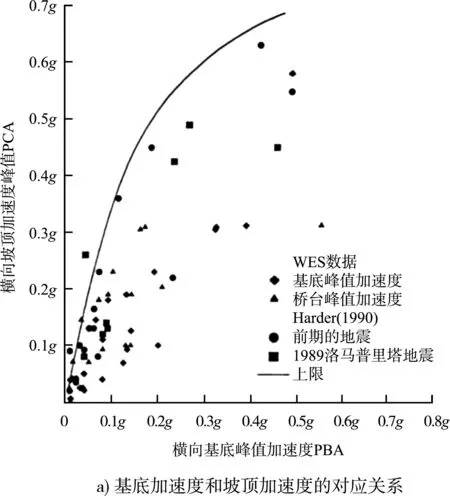
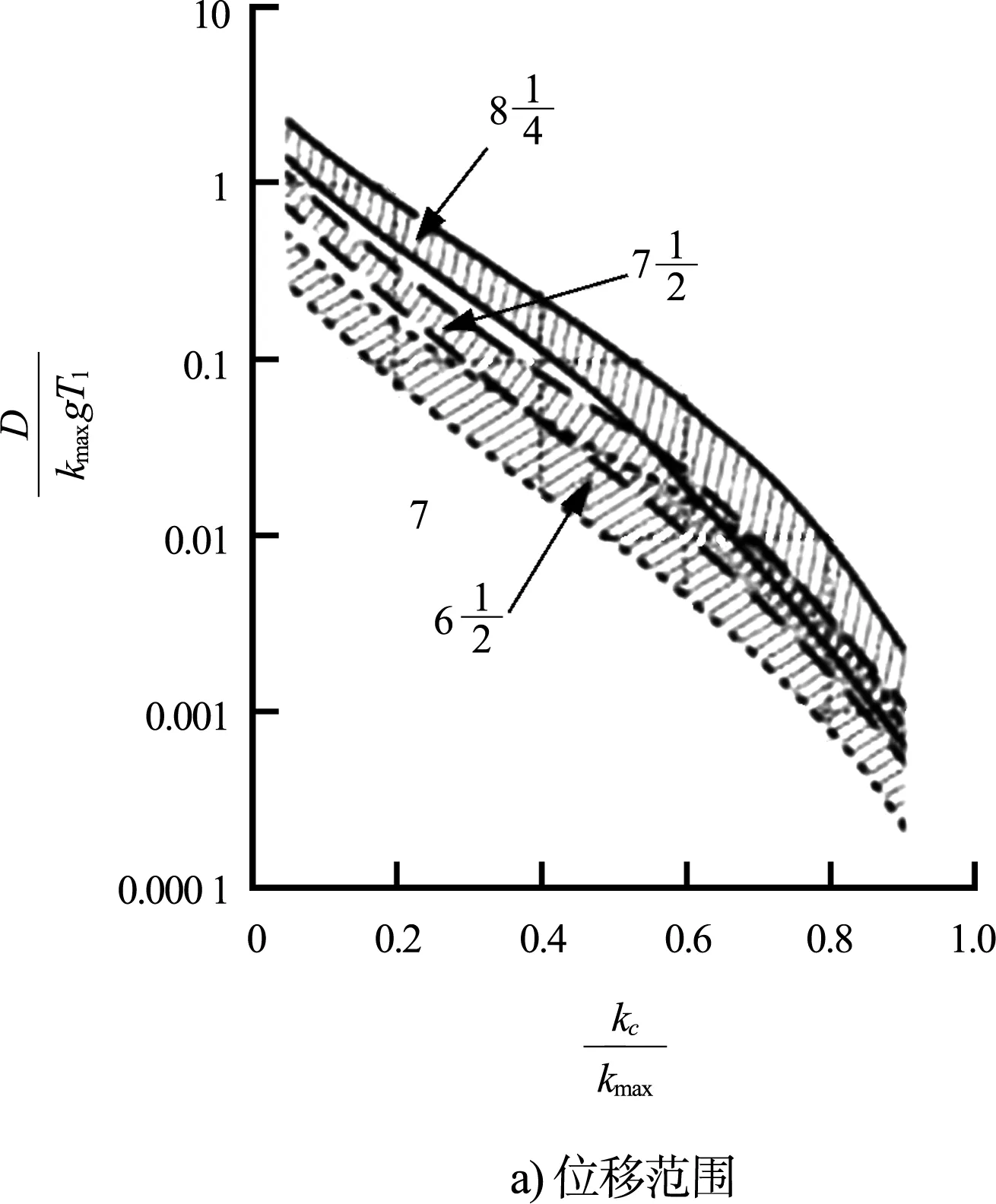
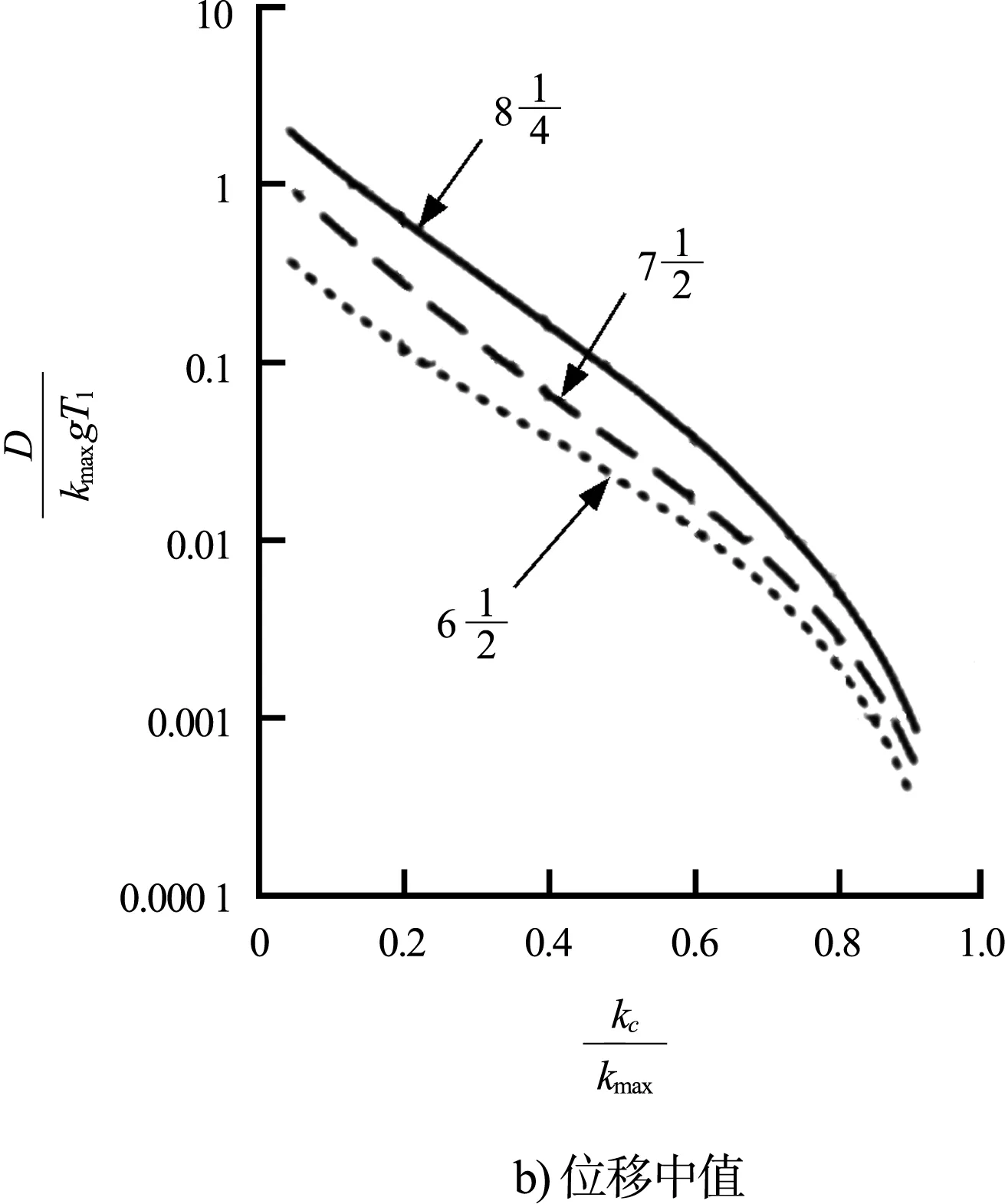
圖4 不同地震震級下永久位移與臨界地震系數的對應關系

3條主要曲線結果如下：

①地震震級為7.5級時，位移采用公式(7)計算：

(7)

式中：D75為7.5級地震下的位移。

②地震震級為6.5級時，位移采用公式(8)計算：

(8)

式中：D65為6.5級地震下的位移。

③地震震級為8.25級時，位移采用公式(9)計算：

(9)

式中：D825為8.25級地震下的位移。

1.2.6考慮阿里亞斯烈度、臨界加速度、峰值加速度

1970年，智利工程師Arturo Arias提出了一種地震動強度的參數[11]，定義為地面加速度的平方在時間上的積分，包含了地震動振幅、頻率以及持時的地震動參數，在表征地震誘發滑坡等地震災害危險性方面具有重要的意義，其表達式為：

(10)

式中：Ia為阿里亞斯烈度；g為重力加速度；a(t)為加速度(m/s2)；t為時間；Td為有效震動持續時間。一般來講，地震的加速度越大、頻率越低、持續時間越長，阿里亞斯烈度越大。

Jibson[12]通過進一步研究，提出了考慮阿里亞斯烈度、臨界加速度及峰值加速度的位移計算公式：

lgDN=0.561 lgIa-3.833 lg(kc/kmax)-1.474±0.616

(11)

Shang-Yu Hsieh和Chyi-Tyi Lee[13]通過收集、分析和研究世界范圍內的地震加速度數據，給出了巖基(式(12))和土基(式(13))的最大永久位移計算公式：

lgDn=0.788 lgIa-10.166kc+5.95kclgIa+1.779±0.294

(12)

lgDn=0.802 lgIa-10.981kc+7.377kclgIa+1.914±0.274

(13)

式中：Ia為阿里亞斯烈度。

1.3 地震位移數值模擬

隨著計算機科學的快速發展，利用軟件進行數值模擬計算地震下的永久位移成為分析地震位移最有效的工具。SLIDE 2018是由加拿大RocScience公司研發的一款功能強大的二維邊坡穩定性的分析軟件，其在條分法的基礎上根據極限平衡進行邊坡的穩定性分析，適用于各種類型的土質和巖質；其地震位移分析的核心計算基于美國地質地震局的SLAMMER程序，是目前較為權威的算法；利用該軟件來分析地震作用下邊坡的Newmark位移分析，可以同時考慮剛性、耦合和解耦算法，為地震下邊坡風險分析和工程設計提供客觀依據。

2 工程案例

2.1 工程概況

菲律賓某濱海新城項目，擬吹填造陸形成318萬m2地塊。工程水工建筑物主要為圍堰及護岸結構，永久工程護岸總長度約為10.2 km；護岸結構形式根據使用功能要求和水文地質等因素，不同區段采用斜坡結構或半斜坡半直立結構。

擬建人工島護岸區域水底泥面高程為-13.35～-4.86 m；地貌類型為海島海岸地貌；工程區地質條件復雜，表層軟土具有強度低且壓縮性高的特性，分布不均勻，工程場地土自上而下劃分為多個土層，其中②-1層含砂高液限黏土、②-2層含砂黏土、③-1層高液限黏土層物理力學指標較差，須進行地基處理；深層土的多個亞土層為含砂高液限黏土、高液限黏土、含礫黏土質砂、膠結砂、砂質彈性粉土等[14]，埋深較深且力學性能指標相對較高，不進行地基處理。

堤身主體采用常規的拋石堤結構，堤頂設擋浪墻和景觀平臺，外側采用人工塊體護面，內側設倒濾設施，斜坡段結構的典型斷面見圖5。地基處理主要采用擠密砂樁，根據水深和地質條件等不同，處理寬度為40～75 m，處理深度北島平均為14 m、最大為27 m，南島平均為8 m、最大為13 m；軟土層厚度較薄的區域采用開挖換填中粗砂振沖處理、局部采用拋石擠淤。

根據本項目地震災害專項評估報告[15]，對于項目場地，level 1(72 a一遇)地震加速度為0.28g(地表加速度，已經考慮場地放大,下同)，level 2(475 a一遇)地震加速度為0.44g。

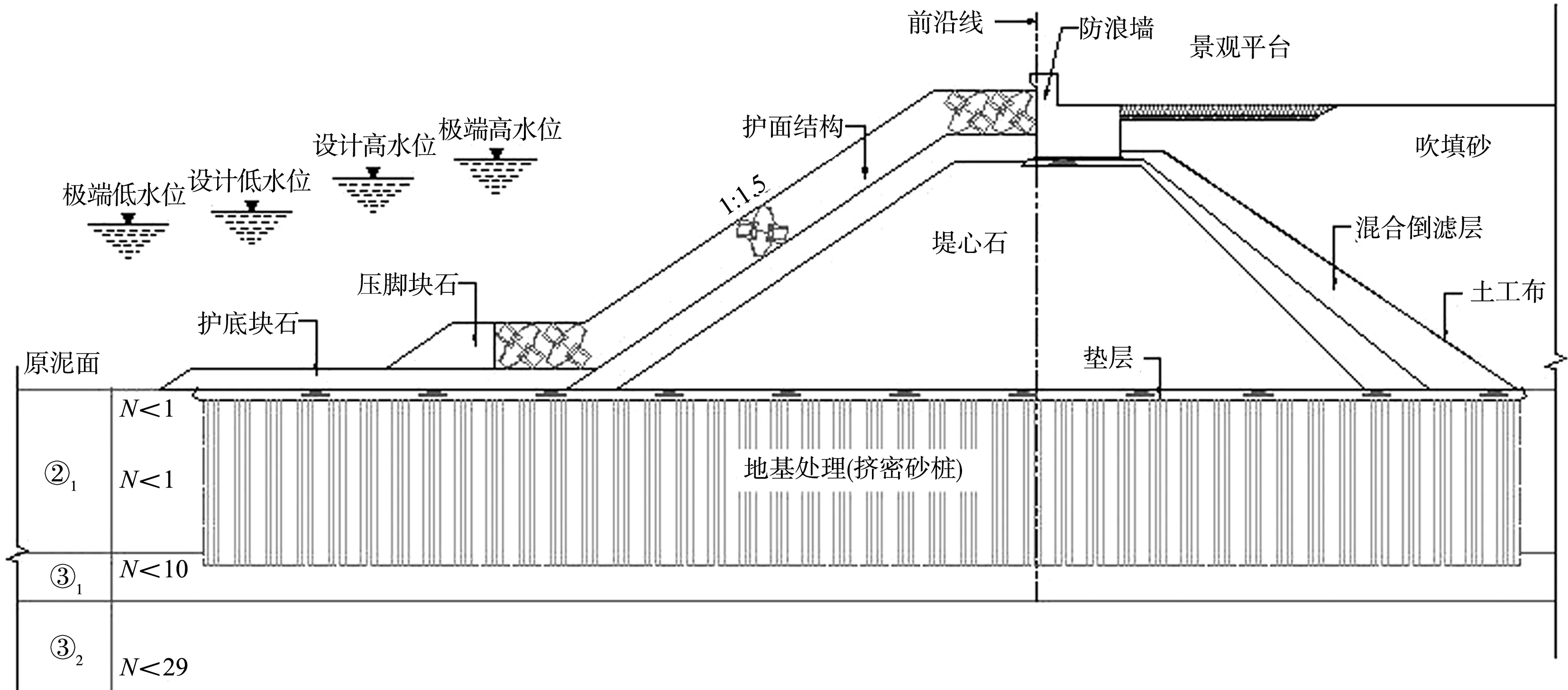
注：N為標貫擊數。

2.2 地震波選取

邊坡的永久位移(地震的破壞性)不僅與峰值加速度PGA有關，同時與地震持續的有效時間、頻率以及地震的阿里亞斯烈度密切等相關。地震波波形不僅僅與地震震級相關，而且與震源深度、震中距離、斷裂帶的距離、場地特征等密切相關。整體穩定分析時，為了盡可能接近場地特征，從數據庫中選取實測地震波，并根據場地特征進行譜匹配。根據地震災害評估報告的建議，選取8組地震32條地震波(其中16條為72 a重現期，16條為475 a重現期)經過目標譜匹配后生成的人工地震波可用于設計。其中475 a一遇地震波的基本參數見表1，不同波對應的加速度反應譜都接近目標譜，見圖6，不同波的時程曲線見圖7。

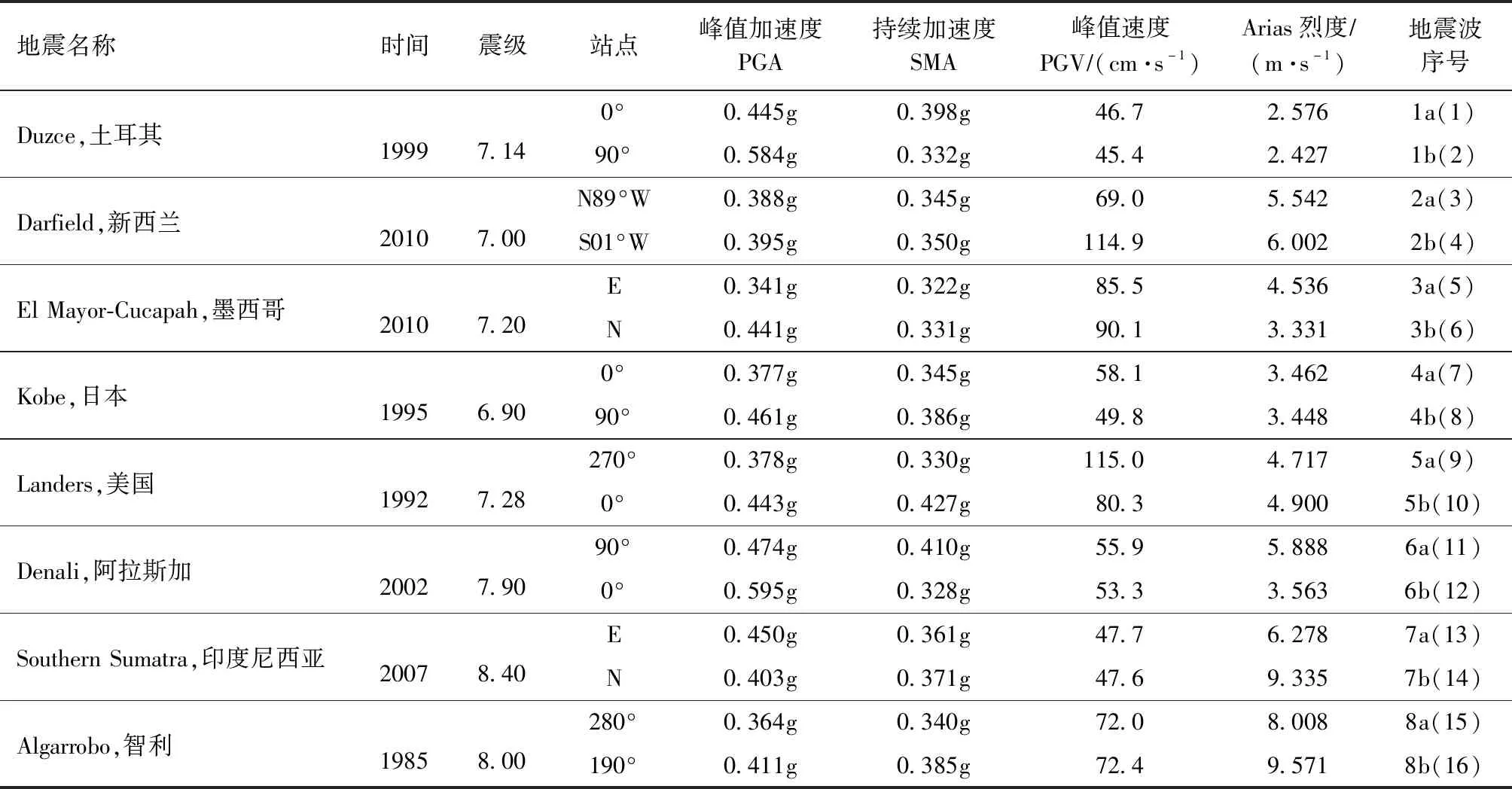
表1 抗震分析計算選用地震波

注：持續加速度SMA為地震波第3大峰值加速度。

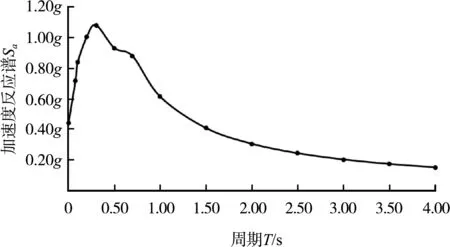
圖6 場地475 a一遇地震反應譜

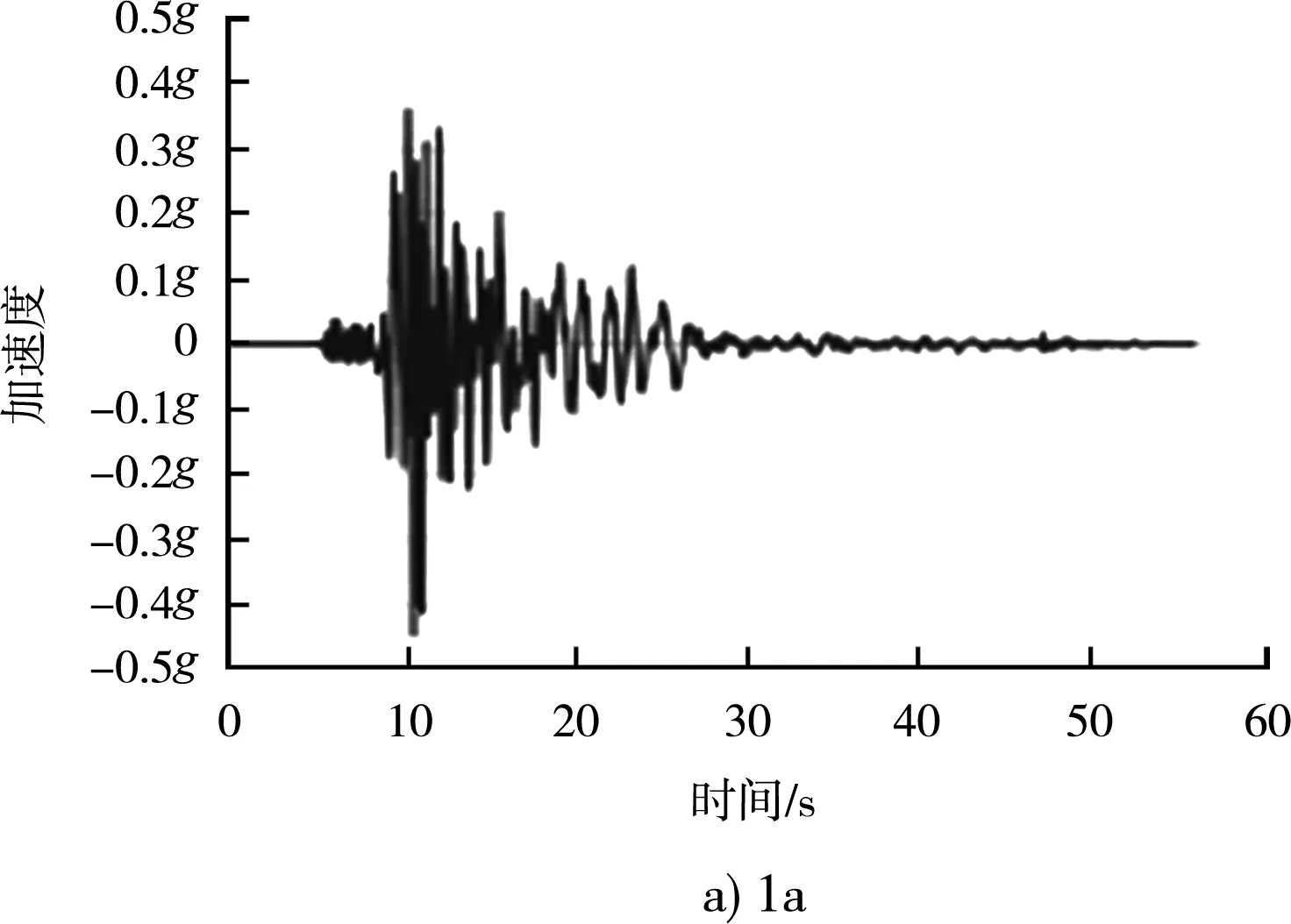
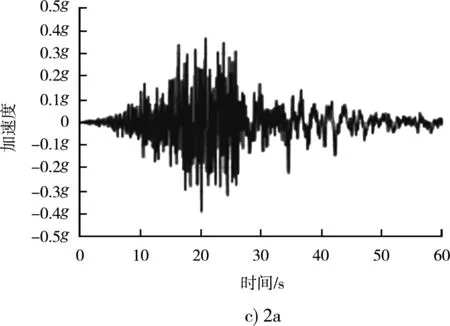
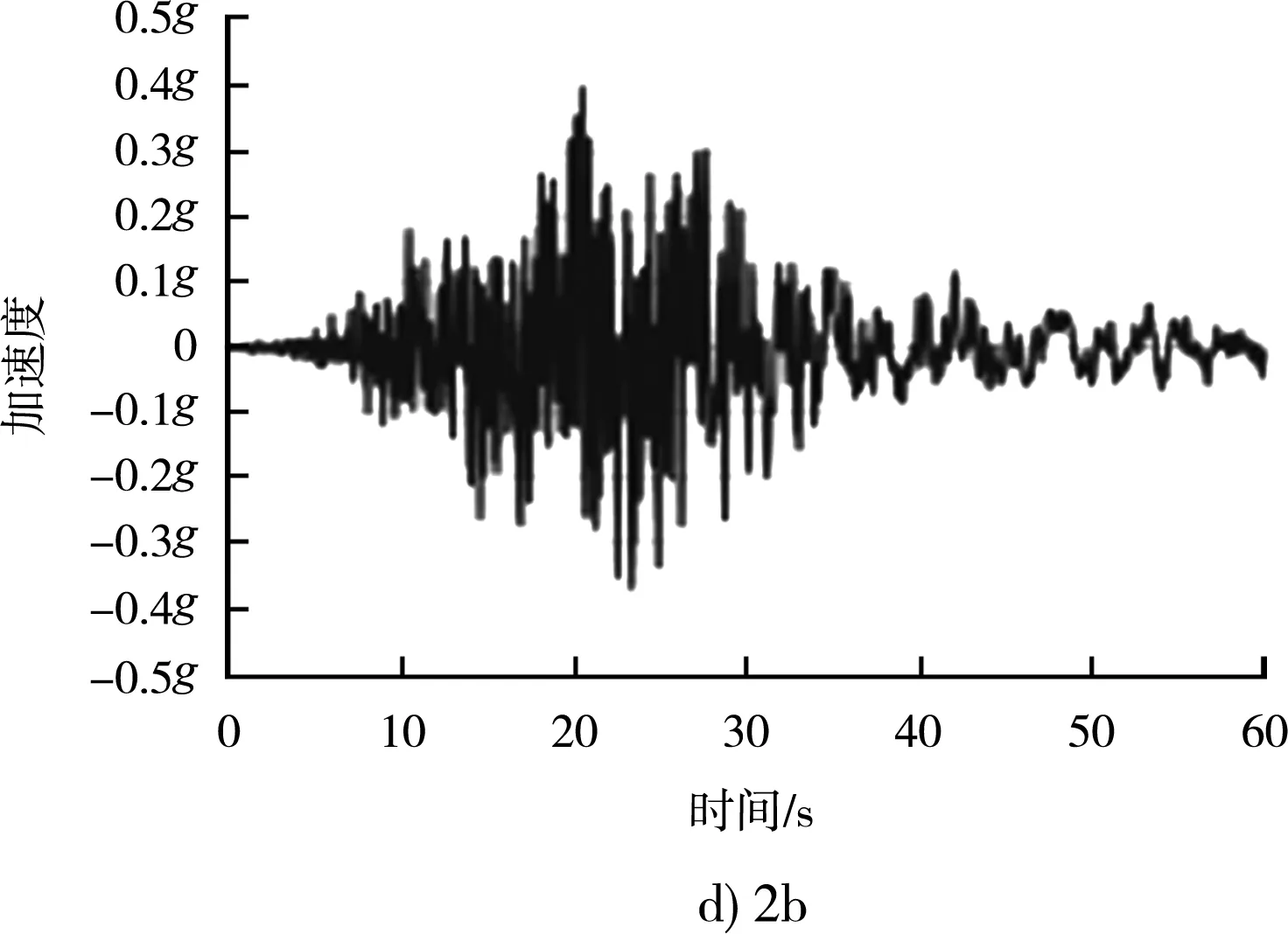
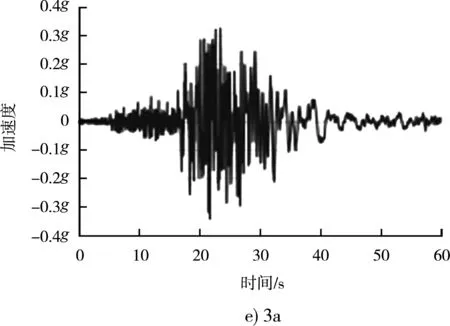
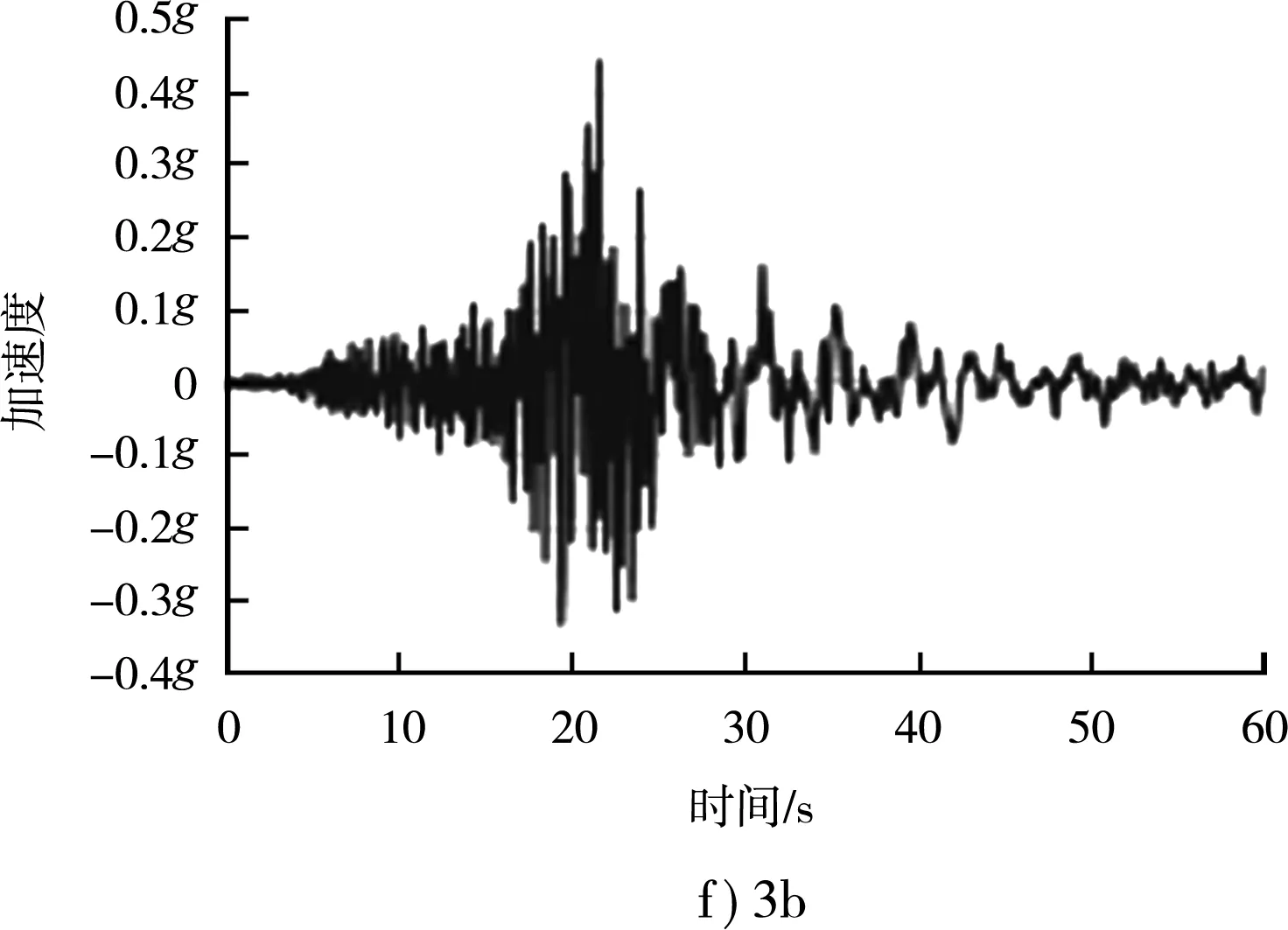
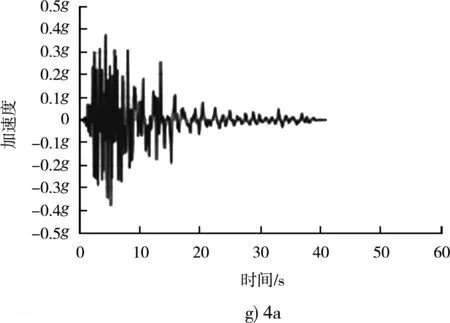
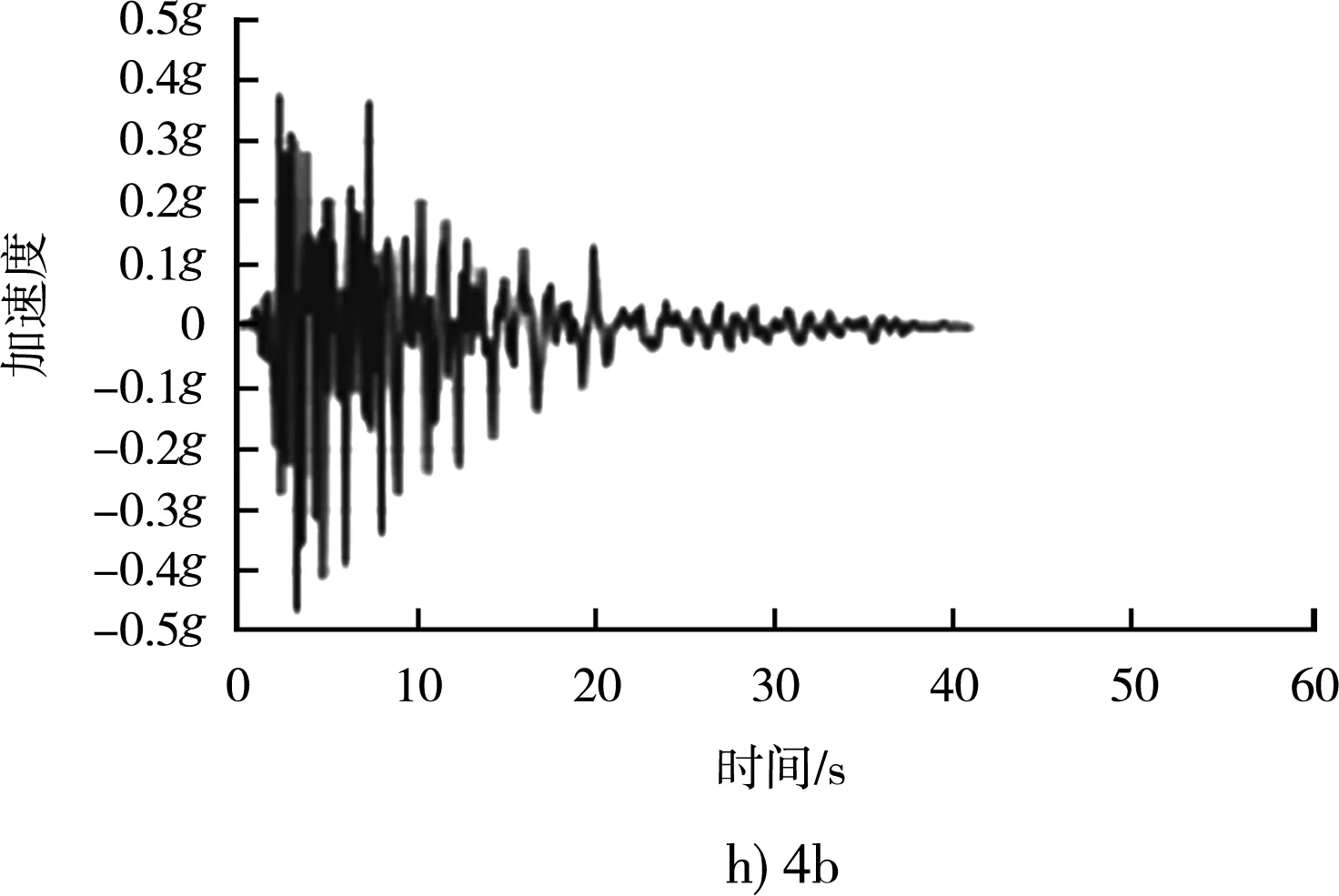
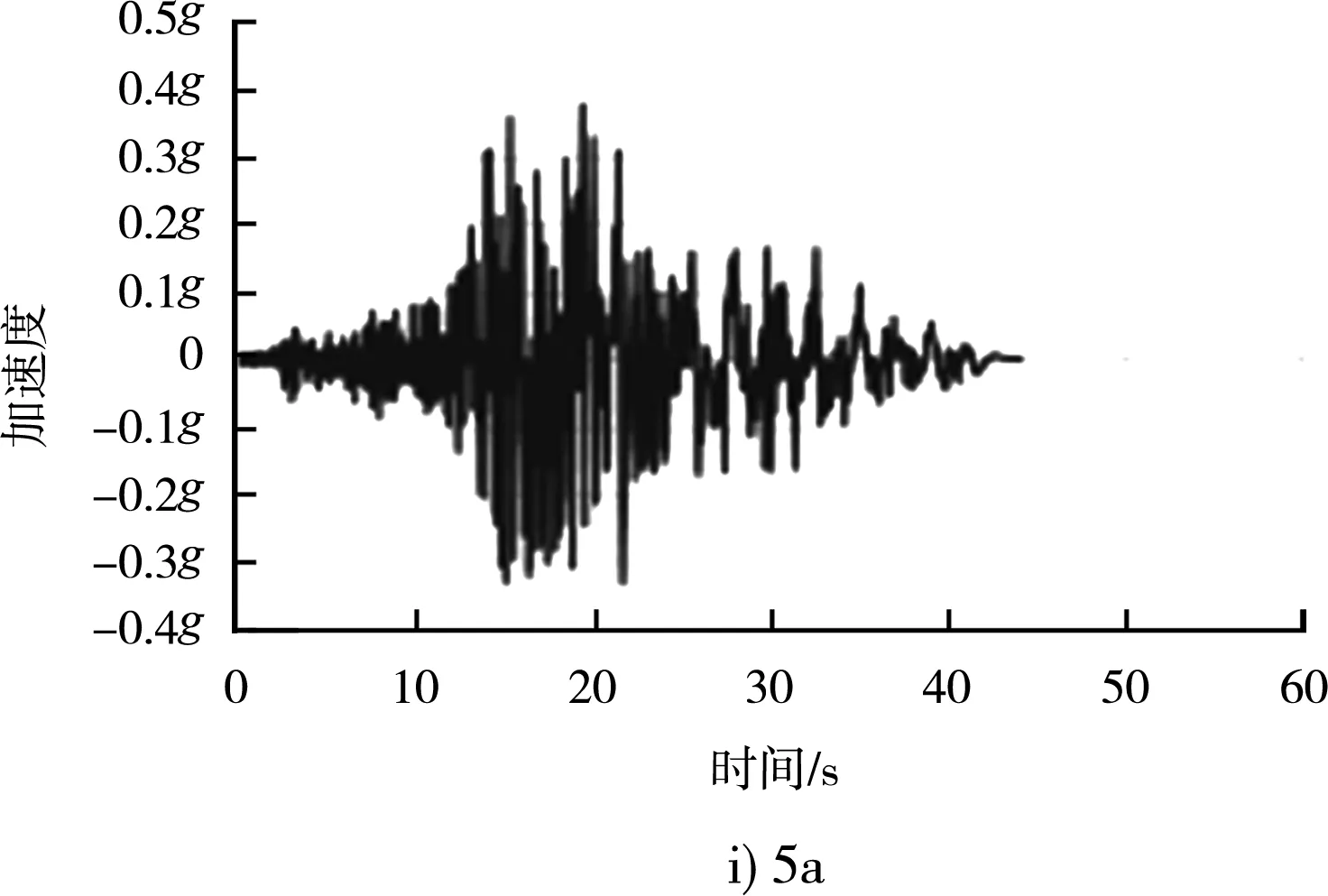
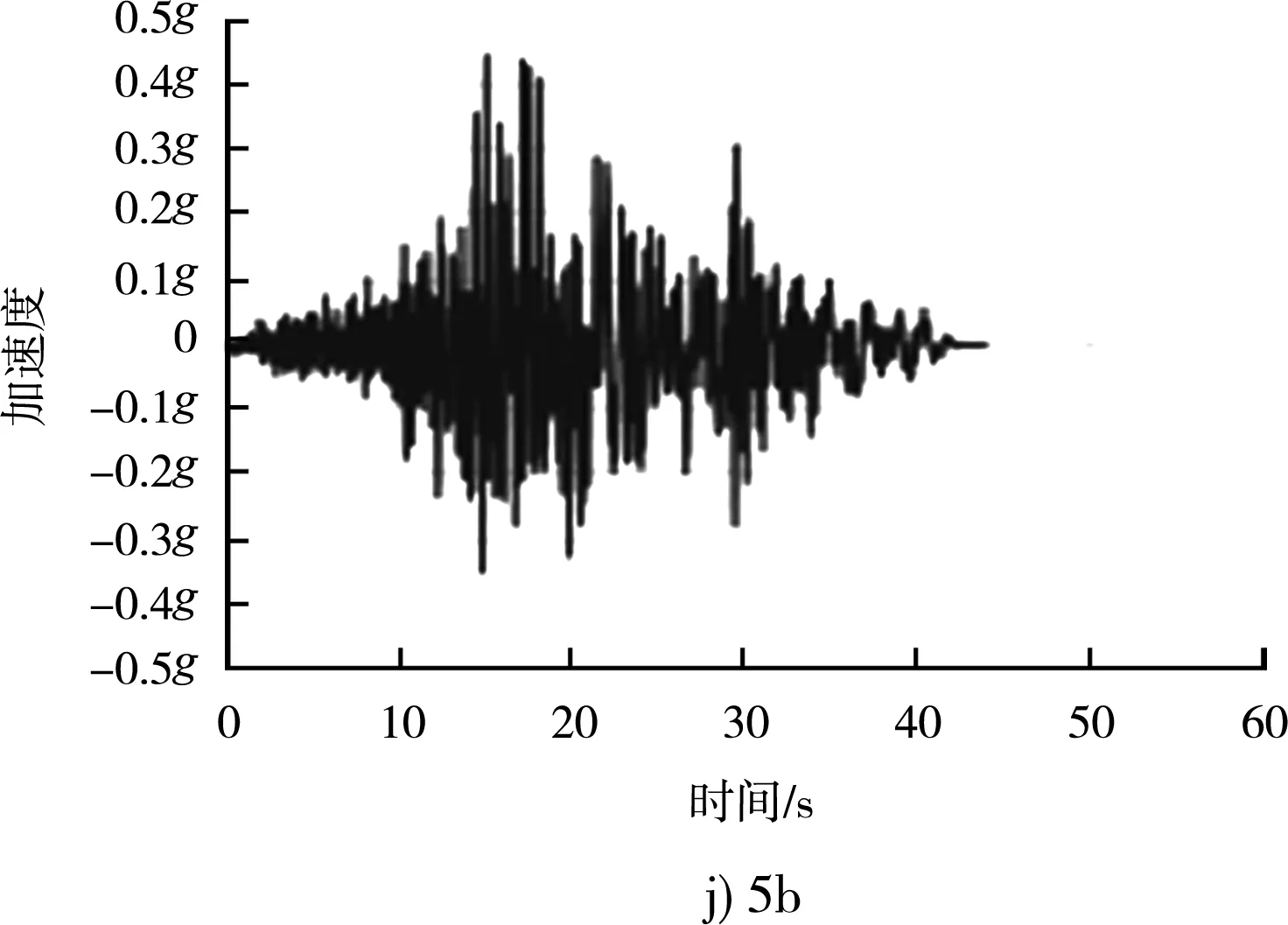
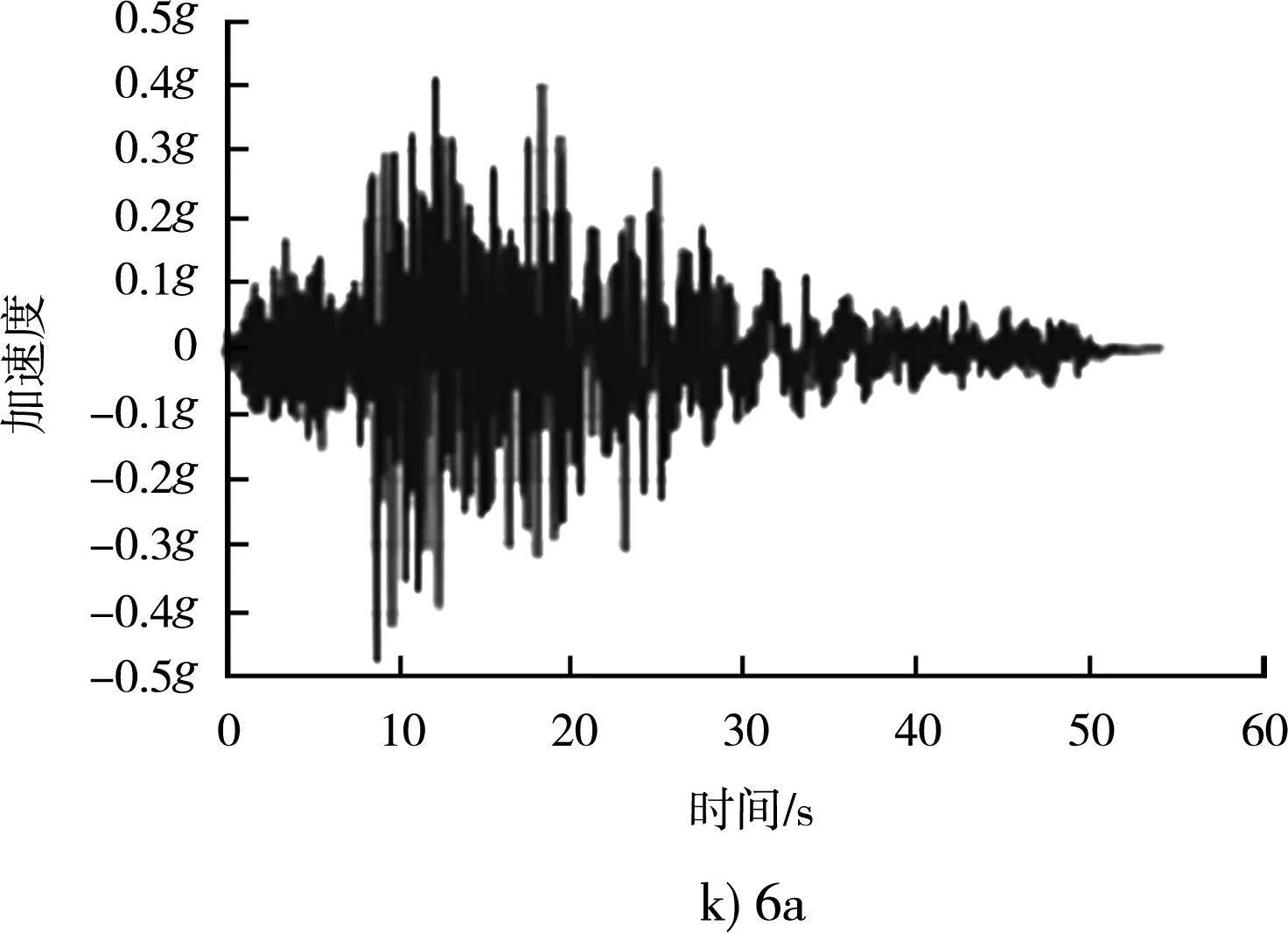
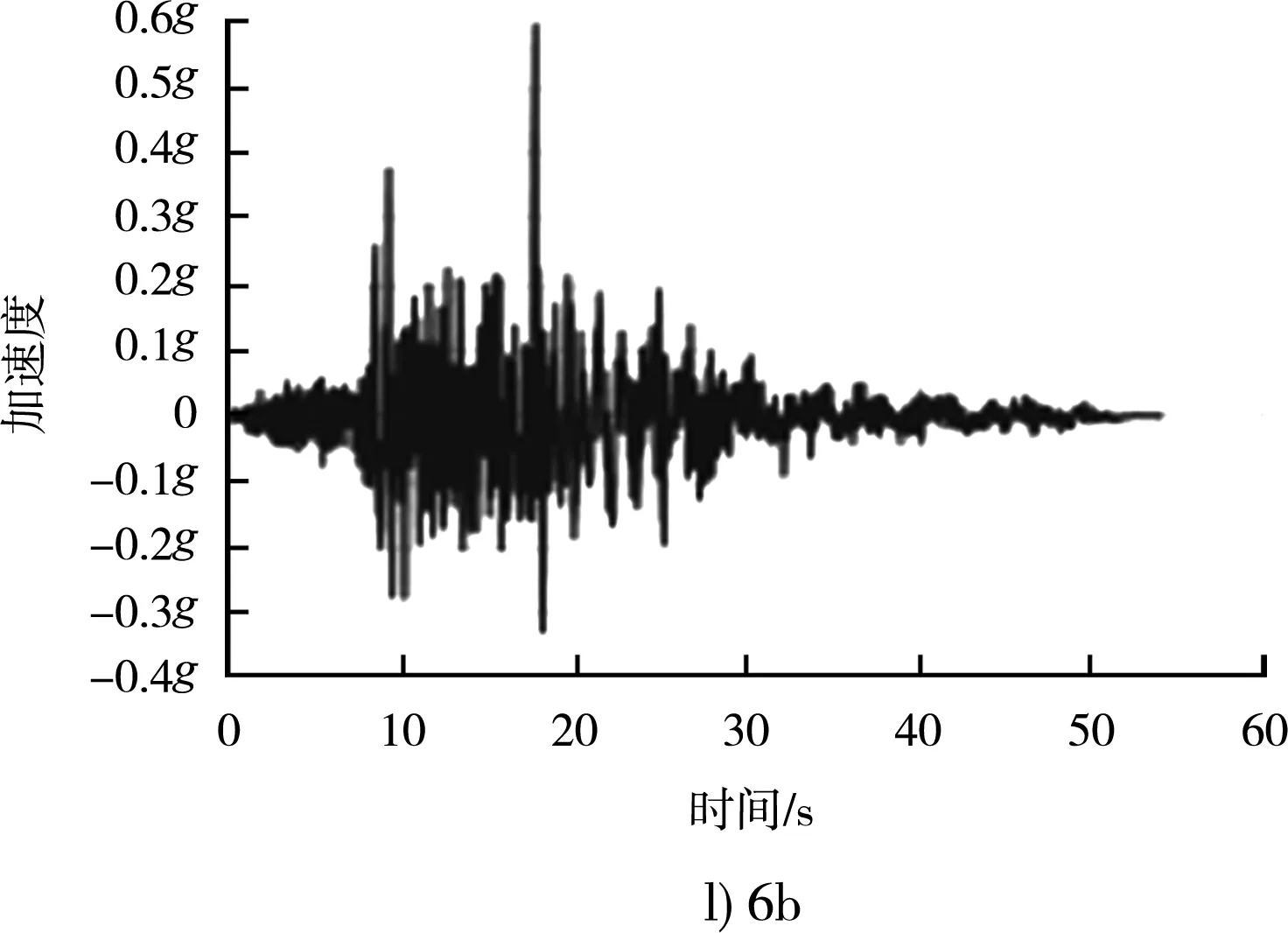
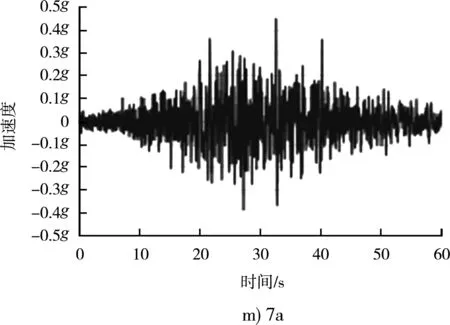
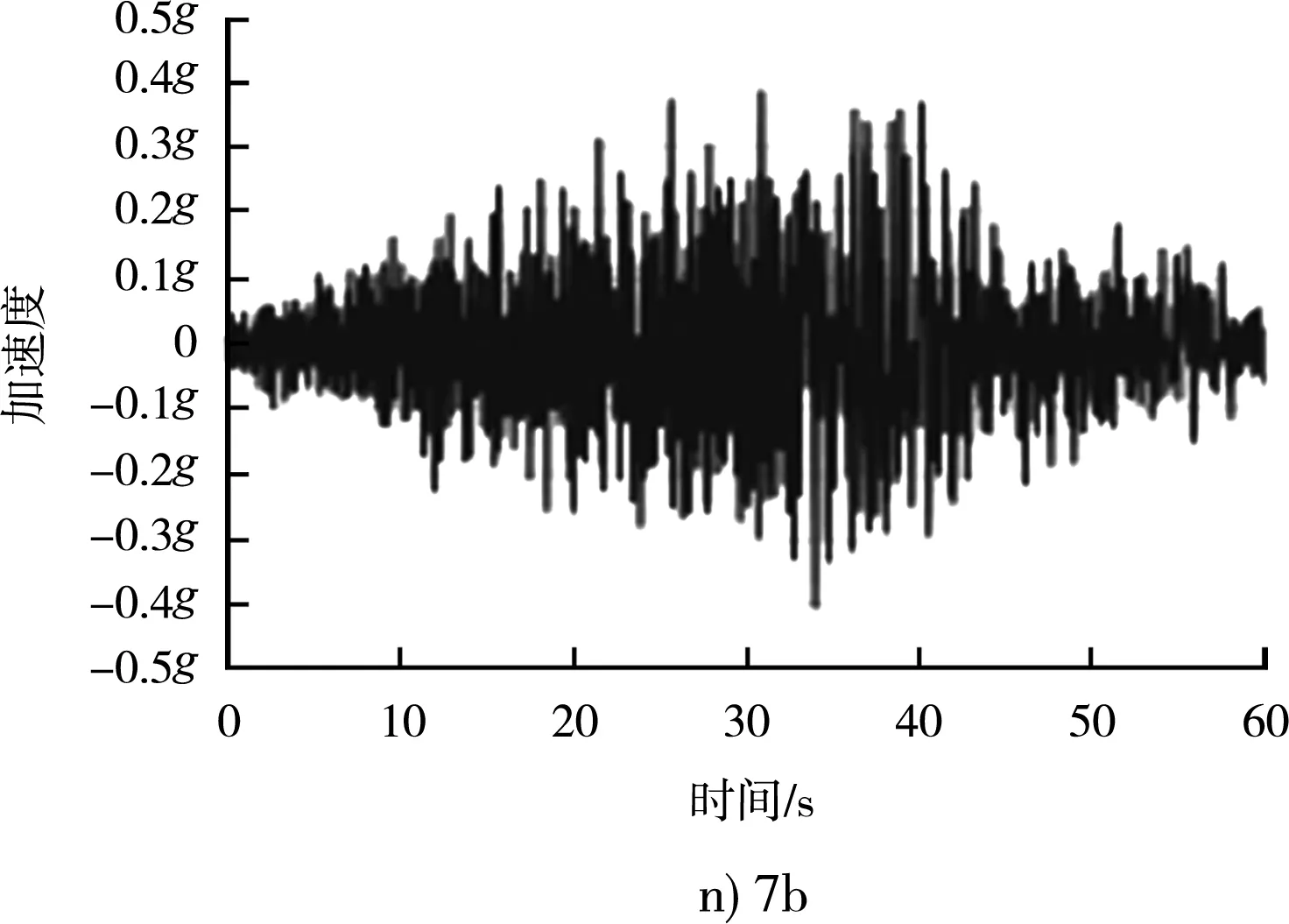
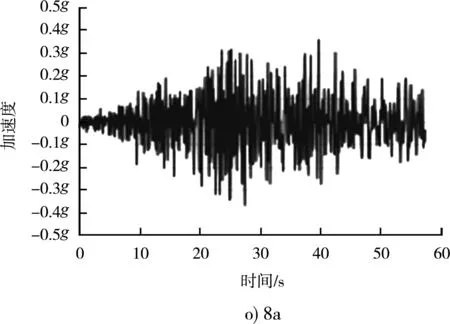
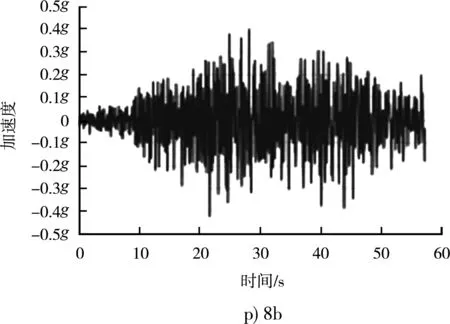
圖7 相同反應譜下不同地震波對應加速度時程曲線

不同地震波雖然差異巨大，峰值加速度、持續加速度、峰值速度、持續時間、阿里亞斯烈度都不一樣，例如1b波峰值加速度為0.584g、8a為0.364g，但對應的反應譜是一致的(反應譜的基本加速度都是0.44g)，都是可以適用于場地特征的，可以用來做工程分析。

2.3 數值模擬分析

位移分析采用SLIDE2018軟件，其核心程序基于美國地質地震局的SLAMMER程序。首先利用SLIDE軟件分析該護岸結構在地震作用下(PGA=0.44g)的整體穩定性，計算方法選用簡化Bishop法。以某鉆孔為例，地震工況下護岸結構的擬靜力分析(地震系數kh=0.5 PGA)整體穩定系數FOS只有0.586，不滿足FOS> 1的規定，因此，需要對地震下結構位移進行分析評價。對護岸臨界地震系數進行模擬分析，計算得出kc=0.098。利用SLIDE軟件自帶的基于Newmark法的地震位移分析模塊，輸入上述擬合的16條地震波，土體模型采用等效線性，阻尼比取0.05，參考應變取值0.05，分別選取剛體算法、耦合算法以及解耦算法3種模型進行計算，得到不同地震波下每個滑動面的永久位移。SLIDE地震位移計算見圖8。

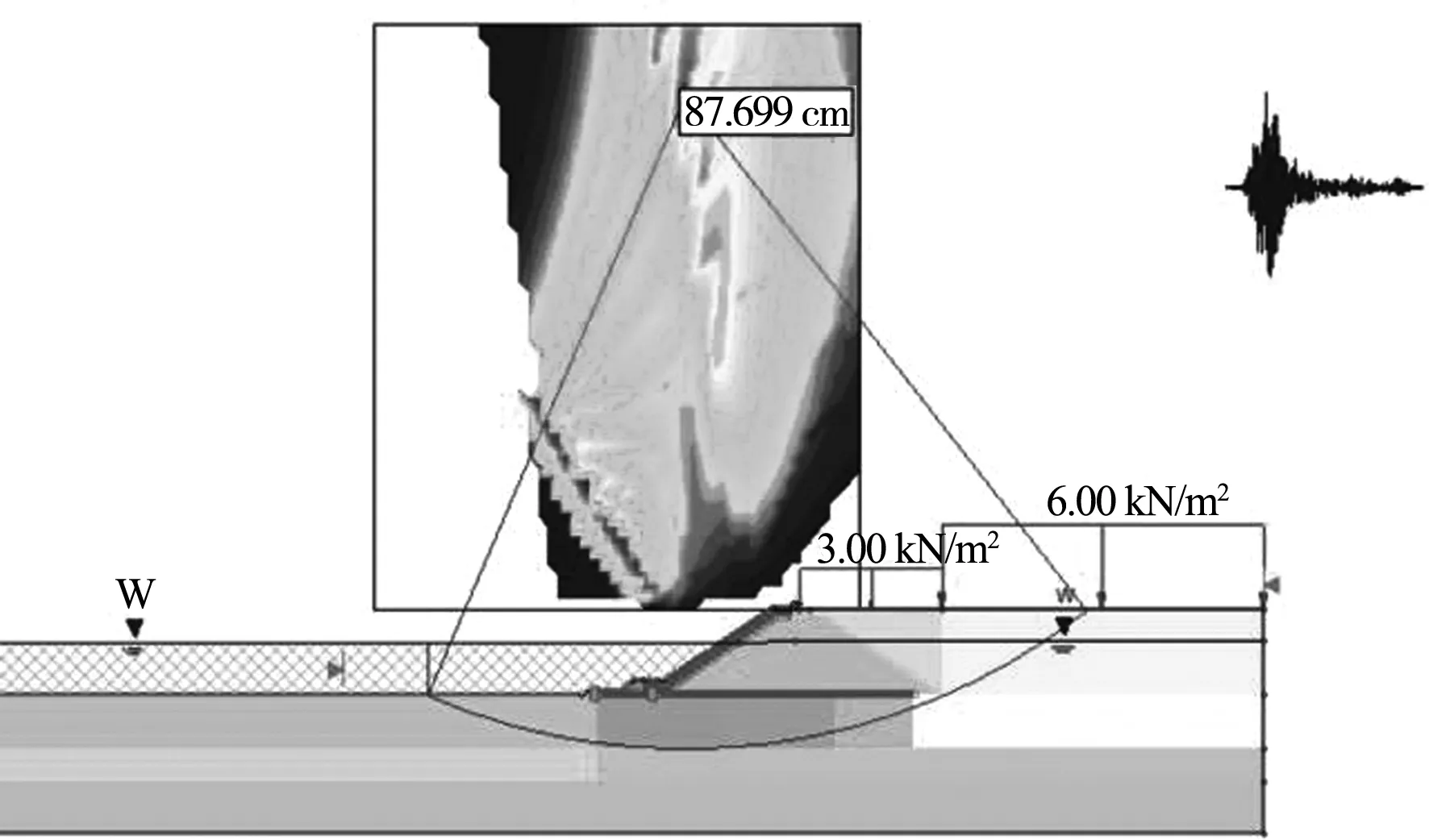
圖8 SLIDE地震位移計算

2.4 軟件與簡化公式計算結果對比

根據SLIDE計算得到的臨界加速度以及地震波主要特征參數，按照上述7種位移簡化公式進行計算，得到相應的最大永久位移值。簡化公式位移計算參數為：峰值加速度平均0.44g，臨界加速度為0.098g(最危險斷面)，阿里亞斯烈度平均值 Ia=5.2，平均峰值速度PGV=69 cm/s，地震震級 Mw=7.6，滑動體高度為25 m，剪切波速vs=163 m/s，滑動體基本周期Ts=0.613 s,1.5 倍周期0.92 s對應反應譜Sa=0.66g。

將SLIDE軟件計算和上述幾種簡化位移計算方法得到的結果進行分析擬合，對比關系見圖9。

對16條地震波進行分析，盡管16條地震對應譜相同，但是波形相差巨大，不同方法的計算差異較大。根據分析可知，目前主流簡化算法考慮的因素主要為統計值，Ambraseys & Menu 公式、Jibson 公式、NCHRP 611算法、Bray and Travasarou法、Makdisi & seed法，均無法反映具體地震波的破壞性。Jibson公式考慮了阿里亞斯烈度，計算結果可以明顯反映不同地震波的區別，Shang-Yu Hsieh、Chyi-Tyi Lee對Jibson公式進行了修正，更好地反映了破壞趨勢，與SLIDE軟件計算結果更加接近。

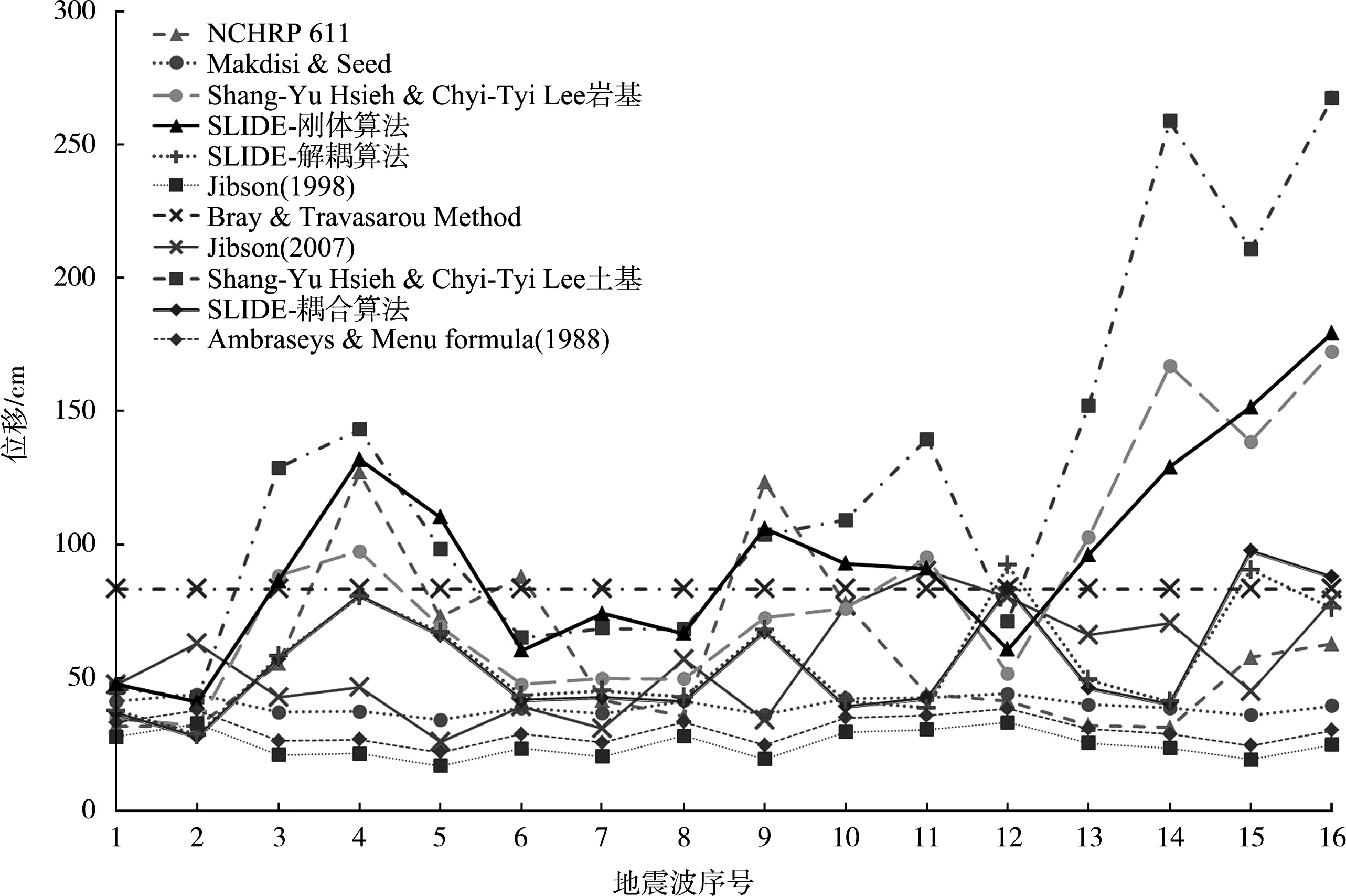
圖9 不同地震波下不同計算方法的位移結果對比

根據國內外相關文獻，地震位移分析仍然以剛體分析為主。也有學者開展了耦合算法和解耦算法的研究，本次抗震設計時，除了采用剛體算法，同時考慮了耦合算法和解耦算法的對比計算，土體模型采用目前國內外學者主流采用的等效線性模型，阻尼比取值5%，參考應變取值0.05。分析可知，采用耦合算法或解耦算法，雖然部分結果更接近于目前常用的NCHRP 611方法和Makdisi & seed法，但是參數設定對結果影響巨大。采用剛體計算方法，與目前國際主流計算結果的大值基本一致，總體上偏于保守的。因此抗震位移分析，采用剛體算法作為基準，計算結論可信。

考慮到計算結果的離散性，本文采用位移計算結果的平均值作為工程設計的依據，即取每目標反應譜下16條人工地震波在同一臨界加速度下滑塊位移的平均值作為控制標準。根據計算結果，設計方案的穩定性滿足本次抗震設計的目標。

3 基于SLIDE結果分析的簡化計算公式

前文的7種簡化算法雖然簡單易用，但相對于SLIDE軟件的精確積分計算而言，部分地震波工程不能很好地反映最終位移與地震參數之間的關系。Ambraseys & Menu 公式、Jibson公式、NCHRP 611算法、Bray and Travasarou法、Makdisi & seed法，可以計算某一地震反應譜基本參數下的地震位移，但是均無法反映具體地震波下的位移，對于相同反應譜不同地震波適應性較差。Jibso公式和Shang-Yu Hsieh公式雖然體現了阿里斯亞烈度，體現了不同地震波的差異，但是由于選取地震波參數的不同，有時誤差較大，未能直接體現阿里亞斯烈度中超出臨界加速度造成破壞的部分。

本文根據項目計算結果的歸納分析，綜合以上簡化算法的優點，提出一種基于有效阿里亞斯烈度和有效破壞時長，基本參數采用阿里亞斯烈度、臨界地震系數、峰值地震系數的永久位移表達式：

(14)

式中：Dm為簡化算法預估平均位移；A為經驗系數；Ia為地震波阿里亞斯烈度；kc為臨界地震系數；kmax為峰值地震系數；γ為經驗系數，反映最終位移與臨界地震系數和峰值地震系數的比值的因素；β為經驗系數，反映同一地震波加速度超出臨界加速度累積頻率相關的因素。

對菲律賓項目不同水深(4.5～12.5 m)、滑弧深度在原泥面以下4～13 m、滑動體高度15～30 m的20鉆孔斷面近720組計算工況數據的計算結果進行擬合和分析總結。由于不同地震波離散性較大，擬合時，kmax取值為0.6 PGA/g+0.4 SMA/g，即0.6倍最大峰值地震系數與0.4倍第3大峰值地震系數之和。根據試算的分析情況，提出兩組近似解：第1組A=5.484，β=3.0，γ=1.0;第2組A=6.221，β=3.0，γ=0.964，式(14)可以進一步寫為：

(15)

(16)

對于不同鉆孔、不同水深和不同計算斷面的16條波位移平均值，大部分斷面的SLIDE計算平均值與簡化算法式(15)平均值誤差在5%以內，個別鉆孔相差10%左右；對于單一地震波，計算位移值的誤差一般在25%以內，個別地震波誤差1倍左右，如圖10所示，主要原因為地震波比較特殊，PGA與SMA相差過大，地震波峰值懸殊。

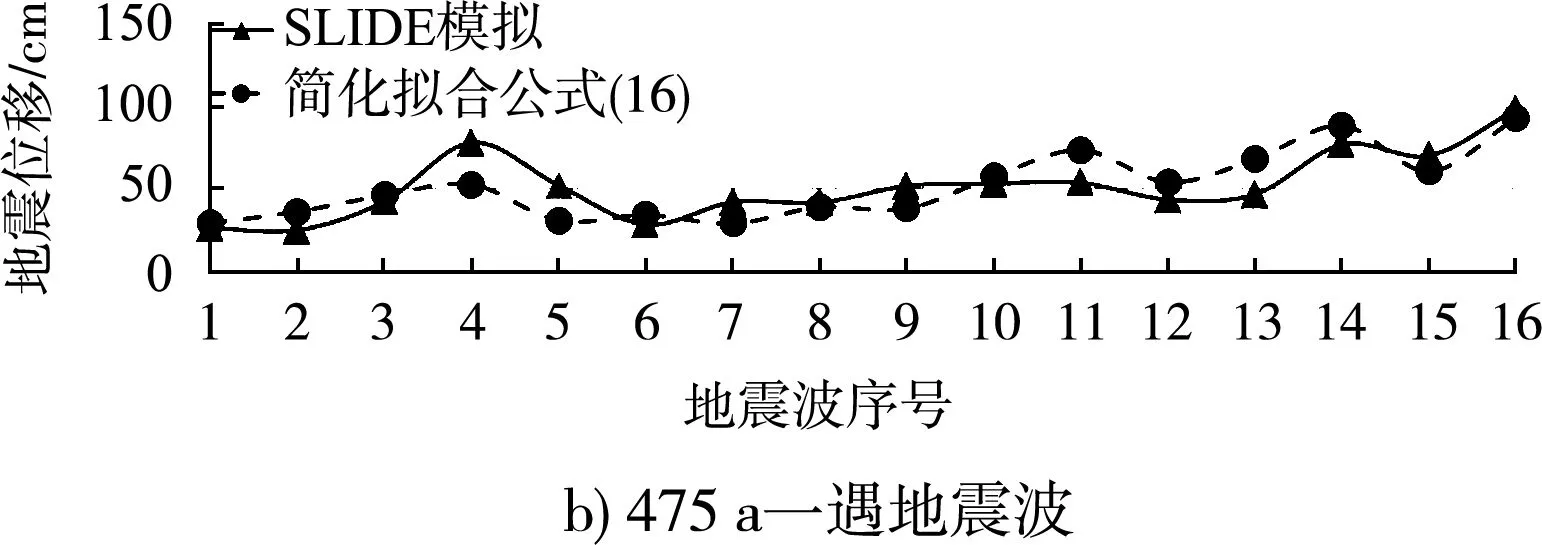
圖10 簡化計算與SLIDE軟件模擬對比

對于同一斷面采用多條地震波平均值統計時，本文推薦的簡化算法適應性較好，類似條件可以參照使用。

4 結論

1)國內規范對于地震工況下的穩定分析常采用擬靜力法，而對于海外項目尤其是位于高震區的工程，從節約工程投資的角度出發，當地震情況下整體穩定系數小于規范要求時，可采用位移分析法對結構的安全性進行評價。采用位移控制的抗震設計方法，更加真實清晰地反映破壞程度，為節省高震區的護岸結構工程造價奠定了基礎。

2)通過對國際上常用的7個地震位移簡化公式和SLIDE軟件的計算結果進行擬合對比分析，驗證了利用SLIDE軟件和其中部分簡化公式進行地震位移計算的合理性和可靠性。

3)地震分析時，SLIDE軟件推薦采用剛體算法，計算結果雖然相對偏保守，但與目前國際主流公式的計算結果基本一致。采用耦合算法或解耦算法時，土體模型的選擇和參數選取至關重要，對計算結果比較敏感，在無試驗支撐時，建議慎重選用。

4)在無地震波的情況下，可以依據地震反應譜的基本參數，使用Makdisi & seed法、NCHRP 611法、Bray and Travasarou法其中之一進行快速評估，但是具體到特定地震波可能會有較大偏差；有具體地震波參數時，可以采用Jibson、Shang-Yu Hsieh、Chyi-Tyi Lee公式對位移進行快速評估，有條件時也可采用Slide軟件進行精確計算。