基于滑模變結構的模塊化多電平鐵路功率調節器直接功率控制

宋平崗， 龍日起， 楊長欖， 雷文琪

(華東交通大學電氣與自動化工程學院，南昌 330013)

由于牽引供電系統普遍采用不平衡變壓器以及兩側機車負載的不平衡，隨之而來的便是各種負序、無功、諧波等電能質量問題。為此，日本學者于1993年提出鐵路功率調節器(railway static power conditioner，RPC)的概念，其不僅能夠維持直流電壓平衡，還可以實現左右兩側供電臂有功功率和無功功率交換、融通。但是由于耐壓水平有限、結構復雜和占地面積大等缺點，未被大規模使用[1-2]。模塊化多電平換流器(modular multilevel converter,MMC)概念于2003年由德國學者提出，其優勢在于輸出電壓等級高、耐壓性能好、開關頻率低等[3]。自此，文獻[4]提出將MMC拓撲結構構建RPC補償裝置，在實現傳統RPC所有功能的同時，兼具MMC拓撲結構的優勢

MMC-RPC由于采用的是子模塊級聯的方式，故不能使用傳統RPC滯環比較的方法跟蹤電流[5]。對于MMC的控制，普遍采用外環定電壓或者定功率、內環電流解耦的雙閉環PI控制策略，其結構較簡單，響應速度快，解耦方便，但不能很好地消除穩態誤差和易受非線性因素影響。文獻[6-8]在模型預測算法的基礎上，分別提出了基于MMC模型的預測控制策略，但MMC拓撲結構的子模塊數量多，開關的組合量多樣，會導致控制器的運算量變得繁瑣，并且控制器對于系統參數過于敏感。文獻[9]提出的直接功率控制，能夠直接在αβ坐標系下對功率進行解耦控制，無需鎖相環的情況下就可以快速精準實現跟蹤參考值，但功率波動問題對系統穩定性有著不利影響。文獻[10-11]提出的傳統的基于查詢開關表的直接功率控制需要生成控制開關動作的開關表，適用于兩電平這種電平數較少的換流器，對于MMC結構而言，開關表的編制較為復雜，無法體現出直接功率控制的優勢所在。

滑模變結構控制是20世紀50年代開始出現的一種控制方法，適用于線性與非線性系統。該控制方法通過切換控制量使控制系統沿著滑模面滑動，對外部干擾和參數樹洞具有魯棒性，且自適應強[12-13]。考慮到滑模變結構控制和直接功率控制各自具有優勢，文獻[14-17]提出滑模變結構直接功率控制并將其運用到風力發電機和PWM整流器等領域，這種控制方法無需鎖相環和同步旋轉坐標變換，不僅動態響應快，穩定性和魯棒性能同樣優越。

雖然SMVS-DPC控制策略在某些場合已經有所應用，但大多集中于風力發電機組，尚未有相關文獻提出將滑膜變結構直接功率控制理論運用到RPC中。為此，提出一種針對MMC-RPC的滑模變結構的直接功率控制策略，在建立單相MMC-RPC數學模型的基礎上，詳細推導和分析該控制策略，同時為了穩定直流電壓，設計針對MMC-RPC的穩壓控制策略。最后在 Matlab/Simulink中建立仿真模型進行仿真驗證。

1 MMC-RPC數學模型與工作原理

MMC-RPC由兩個相互對稱、背靠背相連的單相H橋MMC(single phase H-bridge MMC，SPH-MMC)構成，并聯接入V/v牽引變壓器的兩側。由于左右兩側SPH-MMC結構相同且對稱，故性質、特點相同，所以僅取其中一側的SPH-MMC進行分析與建模。

圖1所示為MMC-RPC左側的基本拓撲結構，子模塊(sub-module，SM)結構如圖1左下，N為子模塊數量。us為供電臂交流側電壓，is為供電臂流入SPH-MMC的交流電流。Ls和Rs分別表示橋臂串聯電感和電阻，L0和R0分別表示為傳輸線路等效電感和電阻，ijp和ijn分別表示流經j相上、下橋臂的橋臂電流(p代表上橋臂，n代表下橋臂)，ujp和ujn為上、下橋臂N個子模塊電容電壓之和,Udc和Idc為直流側電壓和電流。

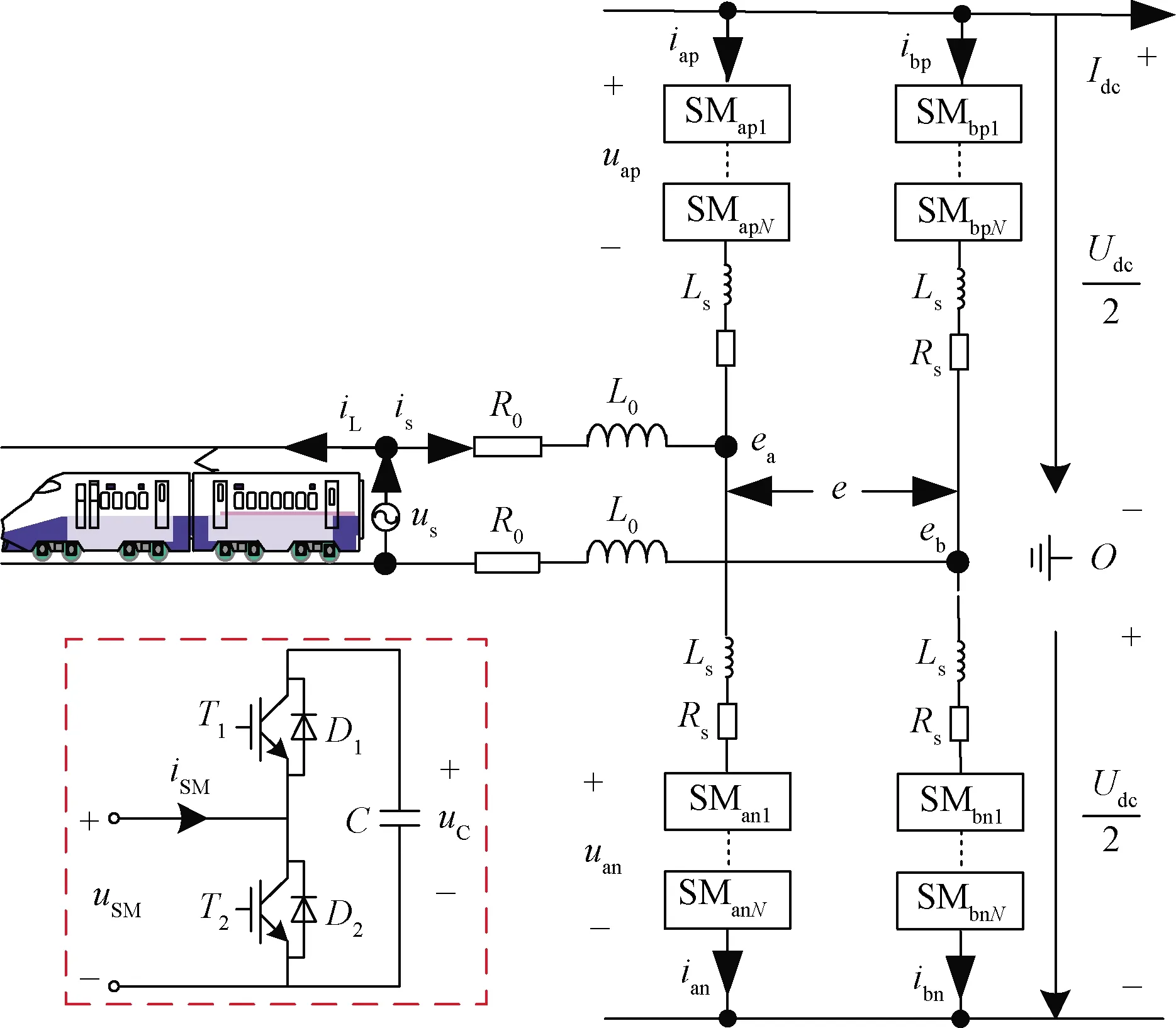
圖1 MMC-RPC一側單相等效電路Fig.1 MMC-RPC side single phase equivalent circuit

由基爾霍夫電壓定律(KVL)，得SPH-MMC交流側數學表達式為

(1)

式(1)中：e為橋臂輸出交流端口電壓，且e=ea-eb。

對SPH-MMC的中間直流側，有

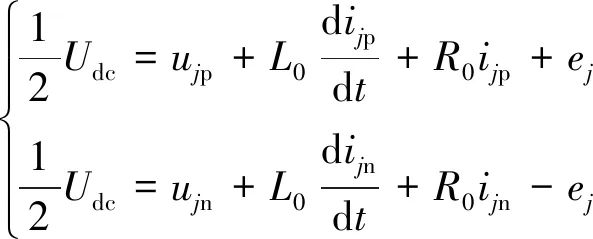
(2)

將式(2)的兩個方程式相加，可得SPH-MMC的直流側電壓

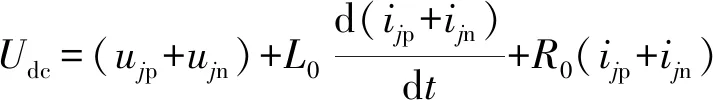
(3)

將式(2)的兩個方程式相減，可得SPH-MMC的交流側電壓：

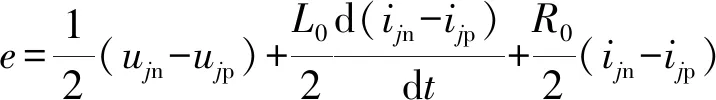
(4)

由式(3)、式(4)可以看出，通過控制橋臂投入子模塊數量來控制上下橋臂電容電壓就能夠實現控制直流電壓和交流電壓的目的。

2 MMC-RPC功率補償原理與計算

2.1 補償功率分析

分析MMC-RPC的功率，令L、R兩側供電臂負載基波視在功率為

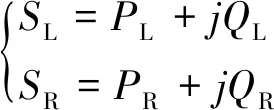
(5)

式(5)中：PL、PR、QL、QR分別表示供電臂左右兩側負載基波的有功功率以及無功功率。

為實現功率平衡，令功率因數達到1，補償效果如圖2所示。

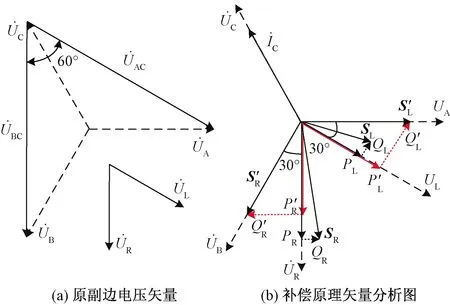
圖2 RPC補償功率前后矢量圖Fig.2 Vector diagram before and after RPC power compensation

經過補償，L、R兩側供電臂需要吸收功率為

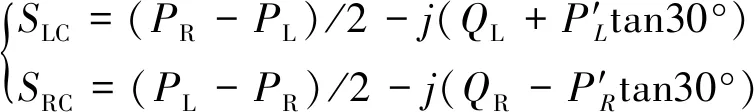
(6)

式(6)中：P′L、P′R分別表示L、R兩側供電臂消耗有功的平均值，滿足P′L=P′R=(PR+PL)/2。

由式(6)可得MMC-RPC的功率補償參考值為

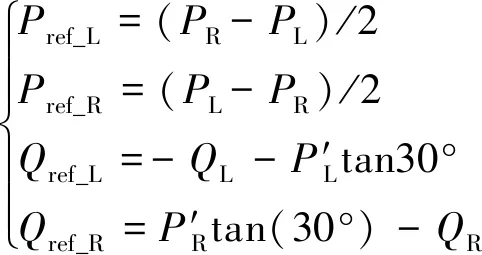
(7)

機車在實際運行時會產生大量諧波，要求RPC能夠實現有功轉移，無功支持的同時，也能夠治理諧波。

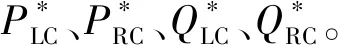
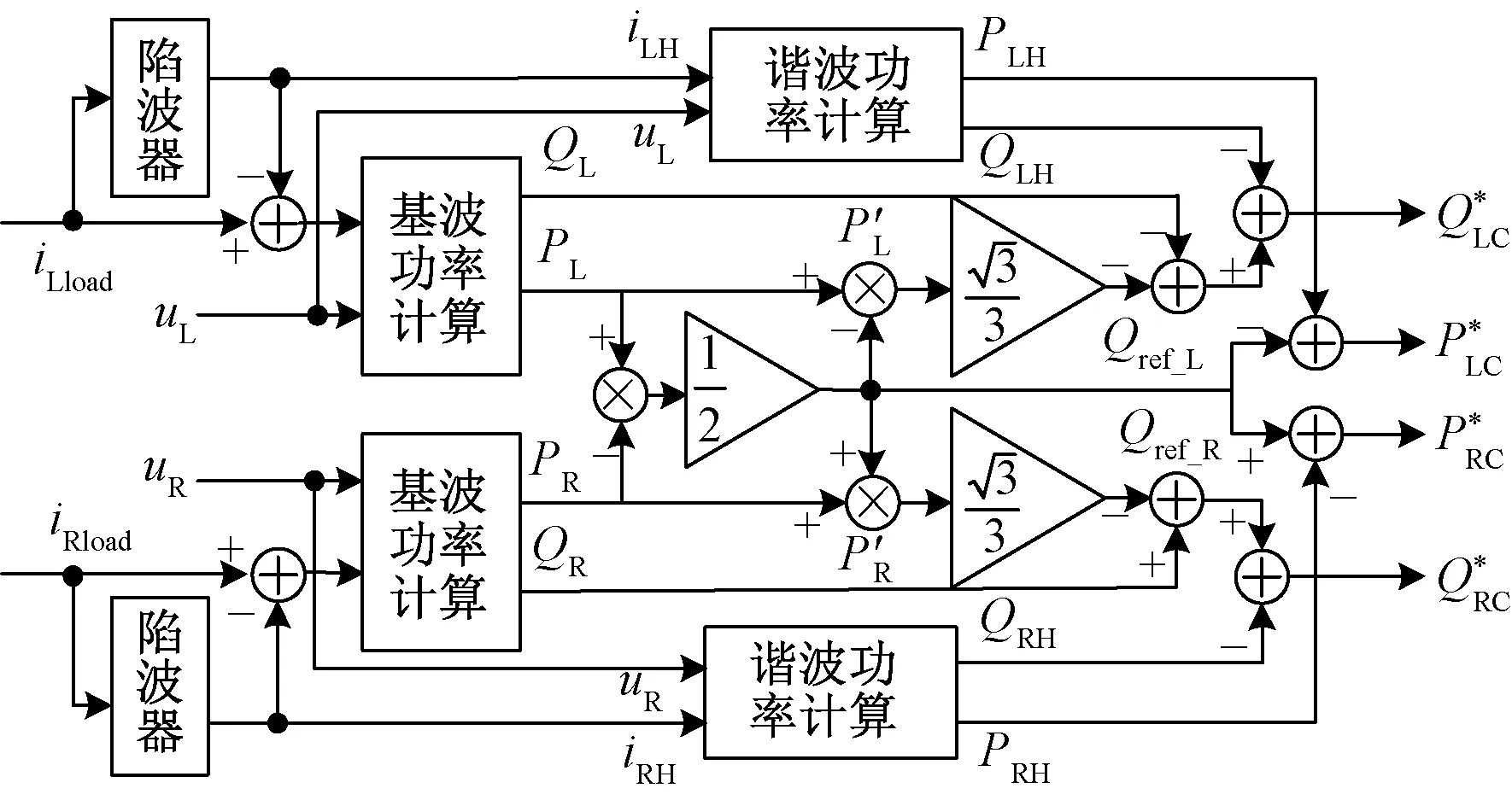
圖3 補償功率計算框圖Fig.3 Block diagram for power compensation calculation

2.2 實時功率計算

由于牽引網采用單相供電方式，SPH-MMC中的交流量僅有單一的自由度，無法使瞬時有功和無功直接分離，因此必須構造與實際交流量正交的虛擬量。構建虛擬正交分量的方法很多，現采用二階廣義積分器(second order generalized integrator，SOGI)[9]，其不僅結構簡單，還具有濾波的作用。構建αβ旋轉坐標系分量fα、fβ和原始信號fs的SOGI閉環傳遞函數為

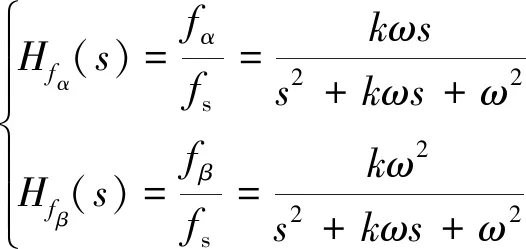
(8)

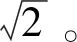
通過SOGI，供電臂交流測電壓us、供電臂流入SPH-MMC的交流電流is可以獲得在αβ坐標系下矢量表達usαβ、isαβ。這樣，就能夠得到單相負載的瞬時有功功率P和Q。

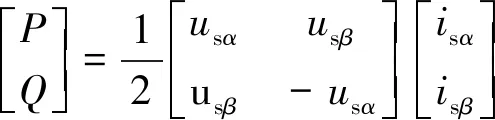
(9)

展開式(9)，得：

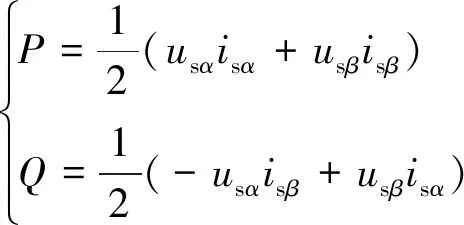
(10)

3 SMVS-DPC控制策略

3.1 SMVS-DPC控制原理與設計

SMVS控制是通過判斷切換函數S的符號，不停地切換控制量去使系統結構發生改變，從而讓系統的狀態變量在預先設定好的空間切換面S=0上，以此完成系統沿切換面運動的目標[12]。該控制器要求滿足滑模存在、可達性、穩定性等條件。由于SMVS控制是一種不連續的開關控制，因而會存在抖動現象，采用趨近率的方法可以改善抖動帶來的影響，加快響應速度和增強魯棒性。趨近率種類多樣，現采用指數趨近率來設計變滑模結構。

為使MMC-RPC交流測的瞬時有功和無功功率能夠實現零誤差跟隨需要補償的參考有功、無功值，選取如下滑模面函數:

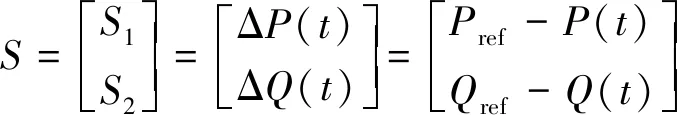
(11)

式(11)中：P(t)和Q(t)分別表示MMC-RPC交流測的瞬時有功功率和無功功率；Pref和Qref分別表示MMC-RPC的有功功率和無功功率補償量的參考值；ΔP(t)和ΔQ(t)分別表示有功功率和無功功率的瞬時誤差。

當系統沿著滑模面運動時，系統處于穩定狀態，此時有S1=0和S2=0，表示瞬時有功功率和瞬時無功功率能夠準確跟蹤參考值，存在：

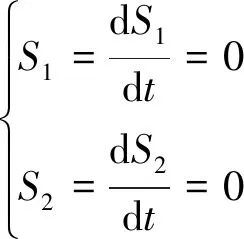
(12)

將式(11)代入式(12)中，得：

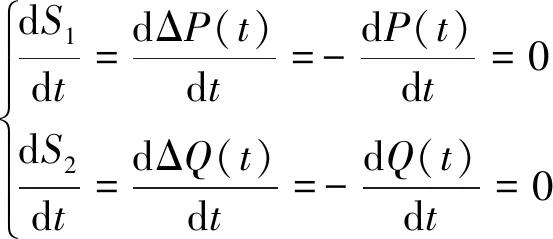
(13)

對式(10)求導，得到瞬時功率變化率為

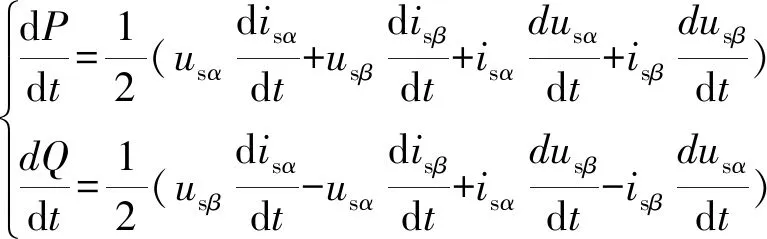
(14)

將式(1)中的交流量通過SOGI構造出兩個互相正交的虛擬分量， 則式(1)可以表達成

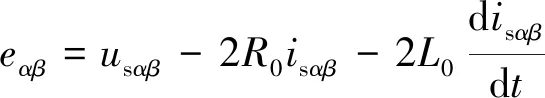
(15)

由式(15)得到isαβ和usαβ的微分表達式為

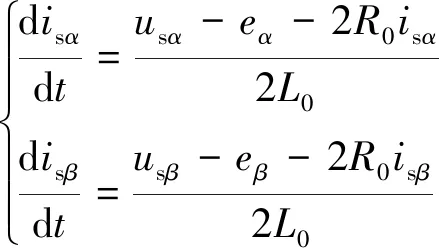
(16)

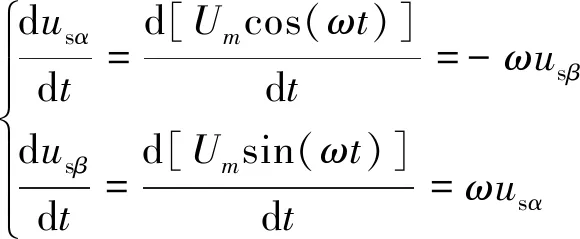
(17)

將式(16)和式(17)代入式(14),可得：

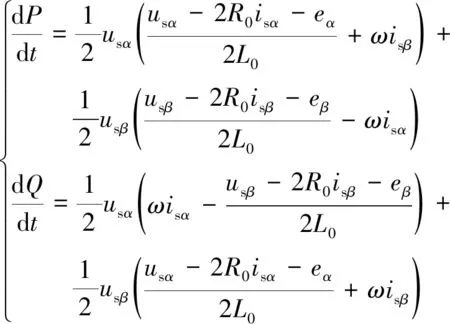
(18)

將式(18)代入式(13)，化簡得到：

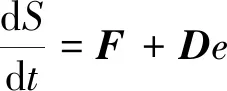
(19)

式(19)中：

由于滑模面切換過程中可能會出現高頻抖動，導致系統出現不穩定，故采用指數趨近率設計SMVS-DPC控制器，并且將傳統的開關函數用飽和函數來替代。文獻[12]對指數趨近率的抖振分析給出了詳細說明。化簡式(19)，得：

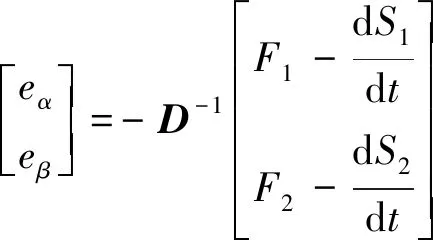
(20)

式(20)中：

dS1=-KpS1-K1sat(S1)；

dS2=-KqS2-K2sat(S2)；

Kp、Kq以及K1、K2控制參數均取正；sat(S1)、sat(S2)為飽和函數；λi表示誤差帶，為正常數，i=1,2。

通過式(20)可以求得SPH-MMC交流端口電壓u，而兩橋臂交流電壓大小相等方向相反，所以求得上下橋臂交流端口電壓ua、ub大小為

(21)

3.2 MMC-RPC直流電壓穩定設計

考慮到背靠背結構的直流電壓對有功功率波動較為敏感，在機車突然投入、切除負載或者過分相時，供電臂的負載會發生突變，導致系統的直流電壓出現大的波動，這不利于系統正常穩定工作，故需要設計如下的直流電壓穩定環節[9]：

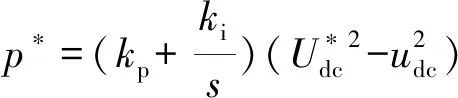
(22)

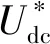
這里的功率參考值p*，同樣可作為SMVS-DPC控制的一個有功功率參考值。

綜上所述，基于SMVS-DPC的MMC-RPC控制的總體控制框圖如圖4所示。

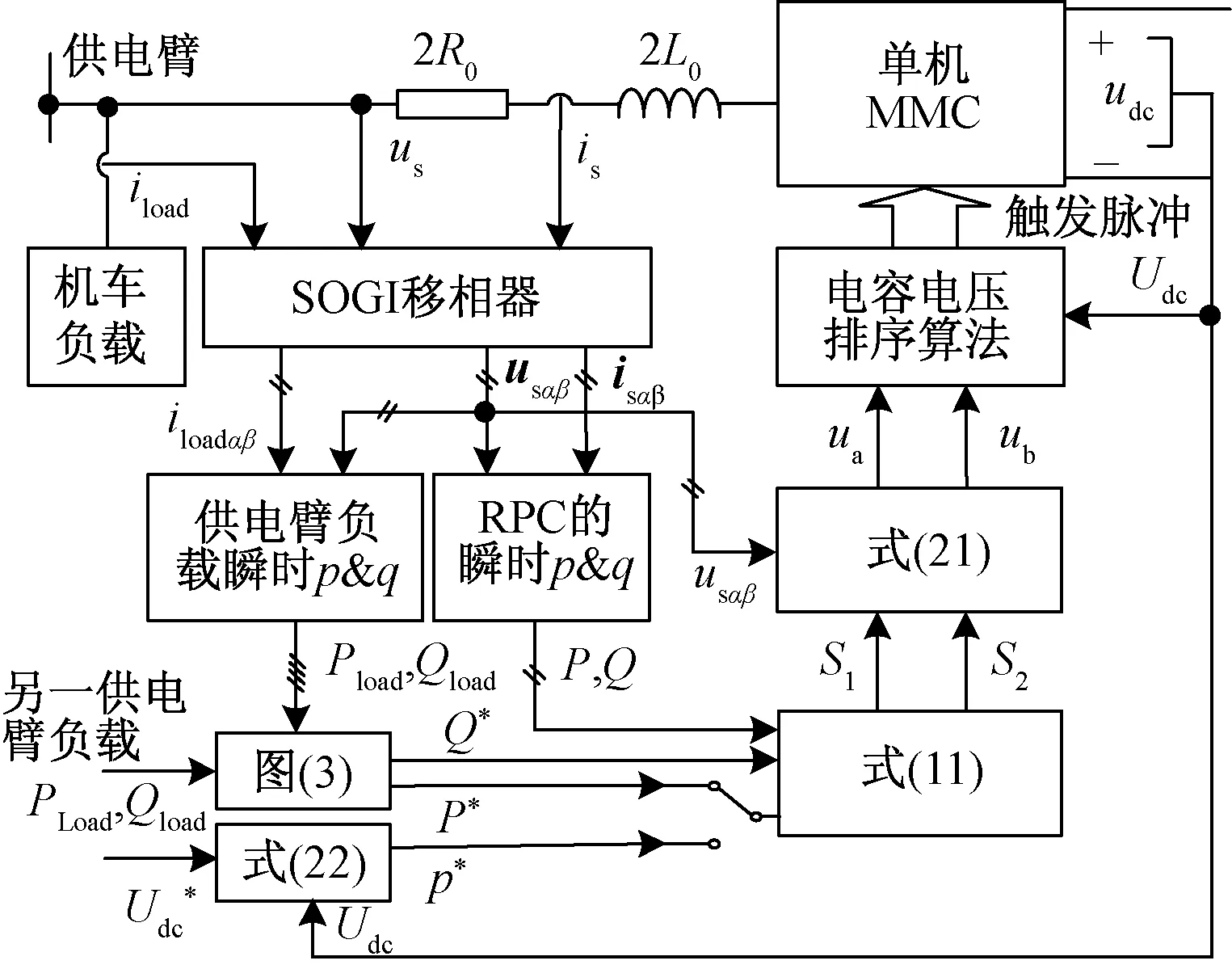
圖4 基于SMVS-DPC的MMC-RPC控制框圖Fig.4 MMC-RPC control block diagram based on SMVS-DPC

4 控制器穩定性及魯棒性分析

4.1 SMVS-DPC控制器的穩定性

選取李雅普諾夫函數：

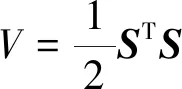
(23)

將上式對時間求導，得：

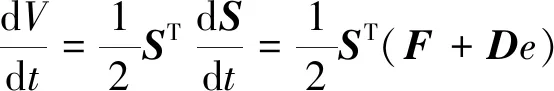
(24)

將式(20)代入式(24),得：

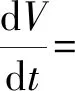
K2sat(S2)]}

(25)

當S1≠0且S2≠0、Kp、Kq以及K22、K21控制參數均取正，則上式中S1(2)與Kp(q)S1(2)+K1(2)sat(S1(2)) 同號，此時必有dV/dt<0恒成立，即dV/dt是負定的。

由式(23)，當S1≠0且S2≠0時，得：

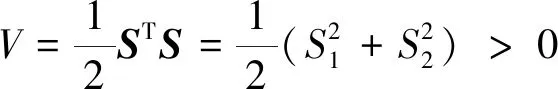
(26)

故V是正定的。因此，由李雅普諾夫第二法可證系統是漸進穩定的，滑模存在且可達。

4.2 SMVS-DPC控制器魯棒性

實際上系統在工作時，線路之間會存在阻抗以及各種誤差和干擾，這些都會對系統的切換函數有所影響。為證明控制器魯棒性，將式(19)重新定義為

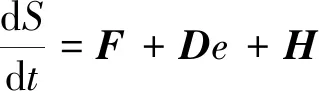
(27)

式(27)中：H=[H1H2]T，為系統的所有干擾之和。

與穩定性證明類似，運用李雅普洛夫離散系統穩定性判斷條件，只要滿足K1>H1且K2>H2，則K1sat(S1)>H1和K2sat(S2)>H2同樣成立，所以[K1sat(S1)-H1]和[K2sat(S2)-H2]大于0，系統仍漸進穩定。故SMVS-DPC具有很好的魯棒性。

5 仿真驗證

為驗證本文提出的基于滑模變結構的MMC-RPC直接功率控制策略的有效性和優越的治理性能，在MATLAB/Simlink中，分別搭建基于SMVS-DPC控制、DPC控制、雙閉環PI控制的MMC-RPC仿真模型進行對比，選取的MMC-RPC仿真參數如表1所示。

表1 仿真系統基本參數

為充分驗證基于變滑模結構MMC-RPC直接功率控制的補償效果，模擬一種機車運行在最為不平衡的情況，即左右兩側僅有一側存在機車運行。設計如下仿真工況。

(1)設計左側供電區間無機車負載，右側供電區機車負載有功功率為16 MW，無功功率為4 MVar，在運行0.15 s后，投入MMC-RPC進行治理。

(2)為模擬機車在負載投切入供電臂時MMC-RPC的補償效果，在0.3 s時刻，在右側供電臂增加有功功率12 MW,無功功率2 MVar。在0.4 s時刻，切除負載至0.2 s時刻之前有功功率為16 MW，無功功率為4 MVar的運行狀態。

(3)為模擬機車過分相潮流反轉時MMC-RPC的運行效果，于機車運行至0.6 s時刻，將右側機車負載轉移至左側供電臂。

圖5所示為模擬工況1的情況下SMVS-DPC控制與DPC、雙閉環PI控制的對比電流仿真波形。

圖5 MMC-RPC補償電流波形Fig.5 Waveform of MMC-RPC compensation current

圖5(a)～圖5(c)與圖5(d)～圖5(f)分別為補償前后左右臂電流iL、iR和V/v牽引變原邊電流iA、iB、iC。從圖5可看出，在0.15 s之前，未開啟MMC-RPC進行治理，左右兩側機車負載不平衡，電流不平衡度為1，產生大量負序電流。在0.15 s投入MMC-RPC進行治理， 左右兩側負載和三相電流很快達到平衡，很好地實現了負序治理的效果。從圖5可知，雖然SMVS-DPC控制和DPC、雙閉環PI控制，3種控制方法均能夠實現RPC基本功能，但DPC和雙閉環PI控制在MMC-RPC投入瞬間會產生較大的幅值波動，而SMVS-DPC控制下則更為平穩地進入負序治理狀態，效果顯著。

在0.16 s時刻通過檢測供電臂電流以及V/v牽引變原邊電流的總諧波畸變率(total harmonic distortion，THD)，可以發現， SMVS-DPC控制下的THD值小于DPC和雙閉環PI控制下THD值，這說明SMVS-DPC控制較DPC控制和雙閉環PI控制，對諧波有更強的抑制能力，體現了SMVS-DPC控制的優越性。

圖6所示為模擬工況1的情況下補償前后左側SPH-MMC有功功率和無功功率波形。

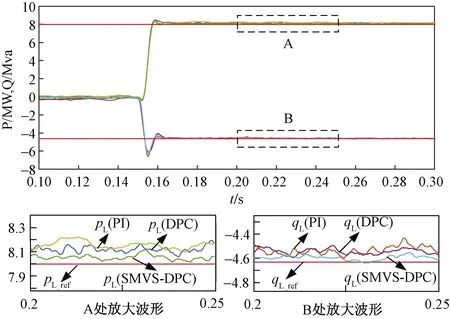
圖6 MMC-RPC補償功率波形Fig.6 MMC-RPC compensation power waveform

從圖6有功功率、無功功率波形放大圖觀察發現，SMVS-DPC控制下的實際功率波形相比較DPC和雙閉環PI而言，在投入MMC-RPC后跟蹤補償功率參考值效果更好，功率波動也較小，能夠更好地進行負序治理，控制效果最佳。

圖7所示為模擬機車在突然投入和切出負載MMC-RPC的治理效果波形。

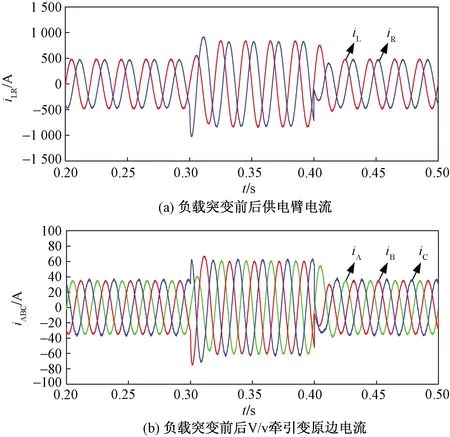
圖7 負載突變情況下MMC-RPC電流波形Fig.7 Current waveform of MMC-RPC under load change

由圖7可知，0.3 s之前機車負載有功功率為16 MW，無功功率為4 MVar。0.3 s時刻，增加機車負載至有功功率為28 MW，無功功率為6 MVar，變壓器原邊電流ia、ib、ic幅值從36 A增加至60 A，整個過渡過程十分迅速。在0.4 s模擬機車負載切除，電流也平穩恢復至原值。不難看出，無論是投入還是切除，系統均能保持三相電流對稱，說明SMVS-DPC控制方法的可靠性，能夠實現在系統突然切入切出負載時，使系統快速達到平衡。

圖8所示為模擬機車過分相時MMC-RPC的治理情況，機車實際運行中不會直接從一側供電臂切換至另一側，這里僅為了模擬牽引系統在極端條件下的控制效果。

圖8 負載過分相情況下MMC-RPC電流波形Fig.8 Current waveform of MMC-RPC under over-phase load

從圖8可以看出，在0.6 s機車過分相時，MMC-RPC能夠實現快速調節作用，雖然由于大量負載切換產生了一定的沖擊電流，但很快實現了三相平衡，整個過渡過程迅速，僅用0.02 s就完成治理，效果顯著。

6 結論

在詳細分析了MMC-RPC的工作原理與數學模型基礎上，設計了可應用于MMC-RPC的變滑模結構直接功率控制器。將該控制器與傳統的雙閉環PI控制、直接功率控制在不同仿真工況下進行詳細的仿真對比，得到以下結論。

(1)提出的滑模變結構直接功率控制策略，可以實現功率調節器的基本功能，能夠快速應對牽引供電系統可能出現的負載變化，有效地治理系統的負序電流，實現系統功率平衡。

(2)控制策略相比較傳統PI而言，能夠直接在兩相靜止坐標系下求得功率，且無需鎖相環跟蹤角頻率，結構簡單，動、靜態性能更為優越。

(3)控制策略相比較雙閉環PI控制和直接功率控制，對系統參數變化、外部干擾以及測量誤差的魯棒性更強，具有更低的網側電流諧波失真。