基于“密鋪”模式下的新圖案生成法式研究
——特魯謝法則延伸與拓展

楊 葉

（南京藝術學院 設計學院，南京 210013）

一、密鋪圖案的由來與發展

密鋪平面（Tessellation）是指一個或多個幾何形狀沒有間隙或不相重疊地平鋪一個表面，可以看做是一種二維平面網格的劃分。早在公元前4000年，蘇美爾人就開始使用密鋪法來建造由粘土磚圖案形成的墻壁裝飾。1619年，約翰尼斯·開普勒（Johannes Kepler）對“密鋪”進行了早期文獻研究。他在《世界的和諧》（Harmonices Mundi）一書中撰寫了有關規則和半規則密鋪的文章，據推測開普勒是第一個探索并解釋蜂巢六邊形密鋪結構的人。

經過一代代科學家和數學家的研究，在20世紀末，1987年，布蘭科·格林鮑姆（Branko Grünbaum）與謝潑德（G.C.Shephard）出版了著作《鋪砌與圖案》（Tilings and Patterns），該書梳理匯總了大量有關密鋪的數理法則，對后世產生深遠的影響。

二維平面密鋪分為周期性密鋪和非周期性密鋪。周期性密鋪圖案（圖1）主要分為規則密鋪（regular tessellation）、半規則密鋪（semi-regular tessellation）和不均勻半規則密鋪（Demi-regular tessellation）。密鋪法的本質是滿足多邊形頂角相接點處內角和等于360°。規則密鋪是指同一形狀的正多邊形密鋪一個平面，只有6個正三角形（內角為60°），4個正四邊形（內角為90°）和3個正六邊形（內角為120°）可以完成密鋪，因為其余正多邊形的內角度數都無法被360°整除。半規則密鋪是指兩種或兩種以上的正多邊形密鋪一個平面，但每一個相接點周圍的正多邊形種類和順序完全相同，這一密鋪法有8種組合方式。以下用（nm）表示這8種組合方式，n為正多邊形的邊數，m為正多邊形的個數，順時針排布：（34，6），（33，42），（32，4，3，4），（3，4，6，4），（3，6，3，6），（3，122），（4，6，12），（4，82）。不均勻半規則密鋪是指兩種或兩種以上的正多邊形的組合密鋪，這一法則的交接點混合了多種密鋪圖形，不同于前兩者須滿足交界點處密鋪圖形完全相同的要求。對于符合不均勻半規則密鋪的圖形組合在學術上一直存在爭議，目前認同的較為精確的圖形組合共有20種，由格倫鮑姆于1987年發表在著作Tilings and Patterns上。此外，約公元600年，從古羅馬、薩珊王朝及拜占庭帝國衍生出的伊斯蘭密鋪圖案也是周期性密鋪模型的重要分支，由于伊斯蘭文化的無神主義論促使藝術家們基于數學探索出了一套完備的圖案裝飾法則，以正方形和圓作為基底展開創作。

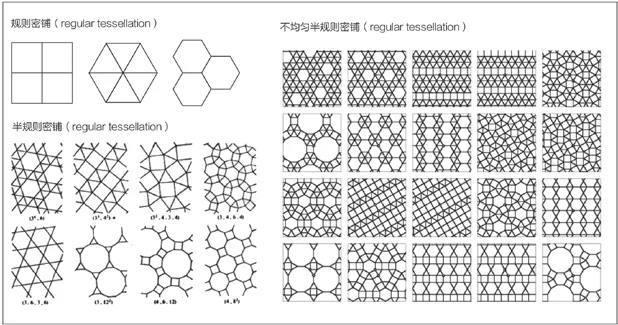
圖1 周期性密鋪圖案的分類

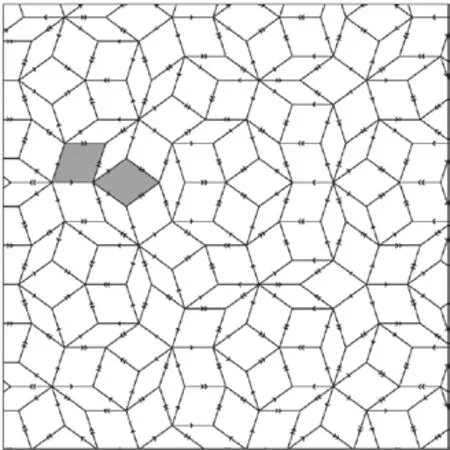
圖2 彭羅斯型密鋪

圖3 特魯謝法則的兩個基本模型

圖4 以正三角形和正六邊形作為框架模件的圖案設計（作者自繪）

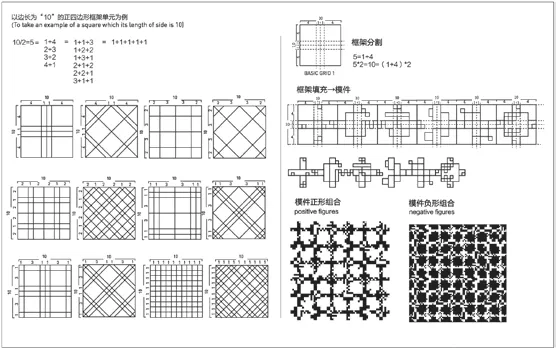
圖5 密鋪圖形框架內模件設計規則（作者自繪）

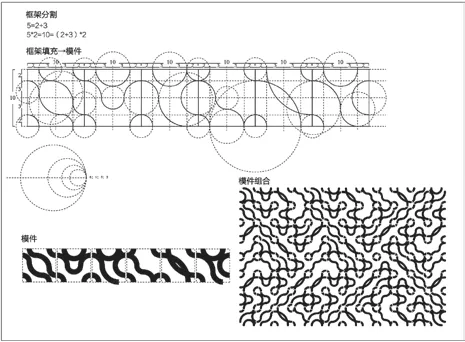
圖6 曲線填充型模件設計（作者自繪）

以上密鋪方式均屬于周期性密鋪，非周期性密鋪的模型也不在少數。彭羅斯型密鋪（Penrose Tiling）是其中著名的模型之一，它是以英國數學家羅杰·彭羅斯（Roger Penrose）命名的。彭羅斯型密鋪共有三種類型，五角星型密鋪（pentagonal tiling）、風箏和飛鏢型密鋪（Kite and dart tiling）以及最為出名的菱形密鋪（Rhombus tiling）（圖2），由一個內角為36°、144°、36°和144°的窄菱形和一個內角為72°、108°、72°、108°的粗菱形拼接得到。

如今，密鋪理論的應用頗多。二維和三維密鋪模型都得到廣泛的發展。如建筑領域中，密鋪圖案在建筑表皮和空間結構的應用；如晶體學領域中，密鋪模式如何優化晶體結構等等。

二、特魯謝法則的延伸（Truchet Tiling）——“中心對稱邊線分割法”

特魯謝法則是在正四邊形密鋪法則的基礎上，提出的對密鋪圖形加入裝飾性紋樣的法則，且裝飾性紋樣具有使正四邊形四邊任意相接的特性。1704年塞巴斯蒂安·特魯謝（Sebastien Truchet）在一篇名為Mémoire sur les combinaisons的文章中首次提及。特魯謝法則主要有兩個模型（圖3）。一是等腰直角三角形模件：沿正四邊形的對角線將其平分為兩個三角形并將其中一個填色。以此模件為基準，通過旋轉、鏡像的手法可以得到該單元共四個方向的模件，這四個模件滿足四邊任意相接的特性，從而通過不同的組合方式可以得到無窮多的拼接圖案。二是1/4圓弧模件：1987年，Cyril Stanley Smith總結了特魯謝的思想，并在其論文中加以推廣，他提出了這一新模型，這一模型是連接正四邊形相鄰邊中點的兩個1/4圓，從而得到兩個不同方向的模件并組合拼接出無窮的圖案。

對特魯謝法則的兩個基本模型展開分析。兩個基本模型實則都是對正四邊形這一滿足密鋪條件的單元形的再設計，然而此處的正四邊形只是作為模件框架存在，它的密鋪性質是隱形的，最后組合圖案的樣式是由正四邊形內圖形的構成形式決定。所以特魯謝法則的密鋪框架單元不是唯一的，與正四邊形具有相同性質的無縫密鋪的圖形框架是正三角形和正六邊形，圖4展示了以正三角形和正六邊形作為框架模件的圖案設計。

接著，對密鋪圖形框架內模件設計規則展開研究。經研究發現，模件必須具備各方向無縫銜接的特點，以滿足“一到無窮”的圖案拼接特性。因此框架內的填充圖形與框架各邊的交點須滿足中心對稱的設計規則。以正四邊形框架單元為例，設正四邊形邊長為10個單位長度，則符合中心對稱的取整數長度的分割法有11種，分別是（1，4，4，1）、（2，3，3，2）、（3，2，2，3）、（4，1，1，4）、（1，1，3，3，1，1）、（1，2，2，2，2，1）、（1，3，1，1，3，1）、（2，1，2，2，1，2）、（2，2，1，1，2，2）、（3，1，1，1，1，3）、（1，1，1，1，1，1，1，1，1，1）。若分割長度取所有有理數，那么分割所得的模件框架是無窮盡的。通過以上分割法的數據，可以設計出圖中所示的模件網格，從而設計出多樣的模件樣式（圖5）。當然，曲線填充型模件的設計，雖不以模件網格為基準，但依舊滿足中心對稱的邊線分割法則，圖6是以邊長為10個單位，按照（2，3，3，2）的分割法完成的圓弧填充型模件設計和組合圖案設計。

當掌握了模件設計規則，試圖思考該規則下模件的變體。目前變體有以下幾個方向：負形、線性、點陣、顏色。因為模件是在分割法規則下誕生的，所以模件的負形亦滿足模件本身的所有特性，如圖7展現了模件負形的多樣性。線性法和點陣法分別是將模件中填充形面的關系變為線的關系和點的組合關系（圖8）。而顏色的填充特別是漸變色的填充常常可以起到改變圖案視效的作用（圖9），從而帶來圖案的縱深感、空間感、膨脹與收縮、實與虛等等特性。對于模件變體的思考有助于豐富模件設計的細節與層次，使得拼接所得圖案更加引人入勝。

最后，是對模件組合法則的擴展。模件都是以密鋪圖形為框架，除了等大排列模件以外，按一定的比例放大和縮小模件亦可排列組合成新的圖案樣式，由于圖案大小的異同，使得組合而成的圖案具有更豐富的節奏與韻律（圖10）。綜上，從“密鋪框架單元”“邊緣分割法”“模件變體”“模件組合方式”四個角度對特魯謝模型展開延伸與拓展，由此獲得一個新的圖案構成系統，筆者稱其為“中心對稱邊線分割法”，此法則的整體設計思路遵循圖11所示的順序和規則。

三、特魯謝法則的意義與價值

圖7 正負形模件（作者自繪）

圖8 線性與點狀模件（作者自繪）

圖9 模件中不同的顏色配比帶來的不同視效（作者自繪）

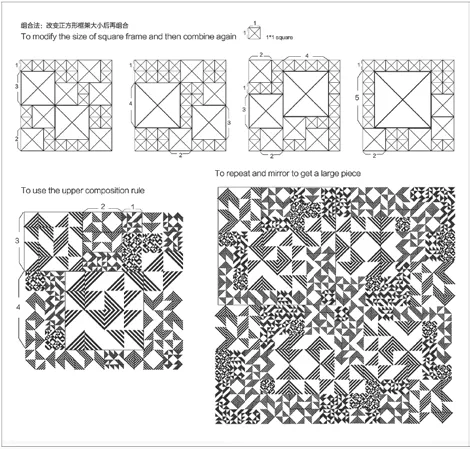
圖10 模件組合法則擴展（作者自繪）

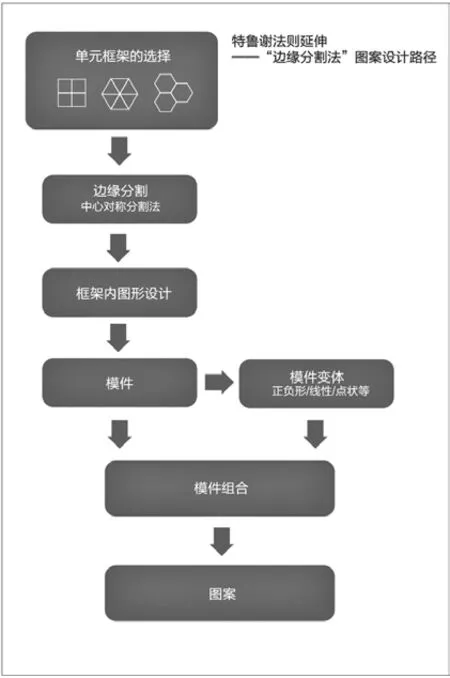
圖11 “中心對稱邊線分割法”設計思路（作者自繪）

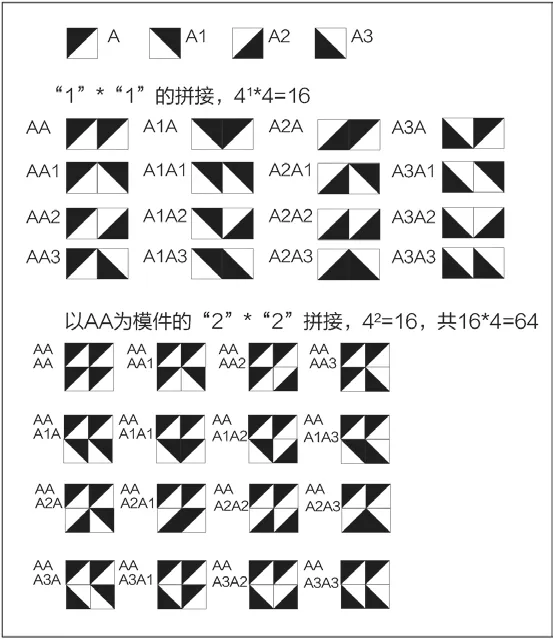
圖12 特魯謝法則的量化（作者自繪）

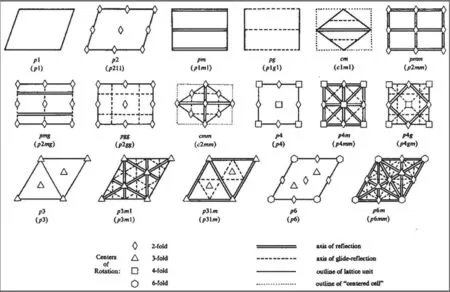
圖13 國際通用17種對稱法

運用數理分析法對特魯謝法則的圖案結果進行分析，通過量化的手法解說特魯謝法則得到無窮圖案的原因，這也是深入探索此法則的重要意義之一。設等腰直角三角形模型的基本模件為A，由此可以得到與此相關的其他三個方向的模件為A1，A2，A3（圖12）。組合A與自身以及其他模件，可以得到“1×1”的新模塊，其中以A為起始的模塊有41個，共41×4=16個。接著，以AA為模件組合自身及其他模件，得到“2×2”的新模塊，其中以A為起始的模塊有42=16個，其他模件的組合方式和AA完全相同，所以共有42×4=64個。其次，以AAAA為模件組合自身及其他模件，得到“4×2”的新模塊，其中以A為起始的模塊有162=256個，以此類推，所有模件的組合共有256×4=1024個。同理，當以AAAAAAAA為模件組合為“4×4”的新模塊時，以A為起始的模塊有2562=65536個，以此類推，所有模件的組合共有65536×4=262144個。至此，研究表明，當模件組合得到的新模塊無限增多時，其組合形成的圖案樣式亦無限增多，呈平方式陡增而達到無窮多個。

因而特魯謝法則具有“一到無窮”的變化特性，由一個或多個滿足特定條件的模件，經組合得到多樣的模塊，模塊的再組形成無窮多的圖案。重要的是，圖案構成方式的視覺冗余度②的高低取決于設計者對模件組合方式的排布，于是呈現的圖案具有多元性：對稱或非對稱，唯一中心或多中心，簡單或復雜，有序或無序等等。因而該法則下組合得到的圖案可以適配不同領域的不同要求，不論是要規避視知覺注意的邊緣性裝飾圖案，還是要引起視知覺注意的具有視覺張力的中心性圖案，該法則都可以滿足實際需求，具有極強的包容性。

相比較當下幾何圖案的其他構成法主要有以下兩種：一是基于1937年安德烈亞斯·施派澤（Andreas Speiser）提出的17種圖形群體組合理論，并于1978年美國數學家多麗絲·沙特施耐德（Doris Schattschneider）以國際標準符號將這17種對稱法則圖標化（圖13）；二是基于密鋪模式體系下形成的密鋪圖案群。這兩種幾何圖案構成法組合的圖案單一、對稱、有序，均具有顯著的易被視知覺識別的重復單元與變換法則，因而視覺冗余度低，圖案包容性弱。人類的審美經驗存在這樣一個基本事實：愉悅存在于單調和雜亂之間。單調圖案的排布會在極短時間內讓我們意識到它的規律，視覺預期會讓我們停止對它的注意。而過于復雜則會使我們的知覺系統負荷過重而放棄對它進行觀賞。

特魯謝法則高包容度的優勢是顯而易見的。重要的是，在當下數字化時代，該法則具有量化為算法和程序的優勢，可結合編程和參數化技術在各行各業發揮重要作用。

注釋：

①“包容性”是指主體對客體的容納程度。英國標準協會（2005）將包容性設計定義為主流產品或服務的設計能為盡可能多的人群所方便使用，無需特別的適應或特殊的設計。這里借用此意，意在指圖案設計容納不同人群審美需求、適配于不同領域的程度。

②這里利用貢布里希《秩序感》中對“視覺冗余度”的引申義，指視知覺對信息數據的感知程度。易被大腦識別、符合視覺預期的圖案組織結構具有較高的視覺冗余度，不易引起我們的知覺注意；相反，不易被識別、違背視覺預期的圖案組織結構具有較低的視覺冗余度，容易引起知覺注意。