常見新型冠狀病毒肺炎疫情預測方法及其評價*

黃麗紅 魏永越 沈思鵬 朱疇文 陳 峰△

【提 要】 自新型冠狀病毒肺炎疫情發生以來，一些學者利用疫情公開數據建立預測模型。所用預測方式包括曲線擬合、傳染病動力學模型及人工智能算法三大類。傳統的曲線擬合預測方式無法考慮傳染病特征，預測結果并不可靠。傳染病動力學模型是本次疫情預測應用最多的一類，能夠考慮傳染病的傳播速度、傳播模式及各種防控措施等因素，但由于考慮的參數不可能全面，且參數可能在疫情不同階段發生動態變化，因此預測效果往往不佳，但對早期預警、防控決策支持及防控效果評價具有重要應用價值。人工智能方法可以綜合考慮不同防控措施以及多種因素的影響，如果考慮得當，預測效果將會有所提高。在綜合利用動力學模型優勢的基礎上，盡可能多地考慮不同影響因素，利用人工智能構建仿真模型，將是一個新的發展趨勢。

自新型冠狀病毒肺炎疫情發生以來，由于人們對新發疾病的認識不足，新型冠狀病毒(國際病毒分類委員會將其命名為SARS-CoV-2)的傳染性被低估，由此疫情初期病毒肆虐，被感染人數不斷攀升，華夏兒女經歷了一場新中國成立以來前所未有的戰役。我國政府統一部署，統籌推進，多措并舉，經過舉國上下的共同努力，綜合防控已取得顯著成效，疫情得到了有效控制。而目前疫情正在全球蔓延，已成為全球共同面對的最重大的生物、醫學和社會挑戰。中國最先以一個國家形式整體積極應對，也在抗擊新冠病毒感染的全部進程中提供了諸多科學研究數據和成果。

在這場驚心動魄的戰爭中，醫務人員首當其沖救治病患，疾控中心工作人員排查疑似病人，尋找密切接觸者，為防止疫情擴散日夜探案。流行病學家對新型冠狀病毒肺炎的流行病學特征已經有了最新認識[1]，為疫情防控獻計獻策；臨床專家不斷總結臨床經驗，逐步明確了新型冠狀病毒肺炎的臨床特征，并在努力尋找新的救治手段。

此次防疫戰，疫情數據透明公開，全世界學者根據每日疫情公開數據，展開各種數據分析，而這其中的焦點，就是對疫情未來趨勢的預測，預測方式多樣，所建預測模型亦多樣。此次疫情中，最常見的預測方法有三大類：傳統的曲線擬合(curve fitting)、傳染病動力學模型(epidemic dynamics model)，以及人工智能(artificial intelligence，AI)方法。本文針對上述三類疫情預測方法進行述評，在介紹各種建模方法的基礎上，結合其預測效果，進行全面分析和對比。

曲線擬合

曲線擬合，又稱非線性回歸(nonlinear regression)，是根據原始資料的性質和實際數據所呈現的趨勢，按適當的曲線類型推算出最可能的曲線回歸，使估計誤差為最小或接近于最小[2]。本次疫情早期，Zhao等基于指數增長趨勢進行曲線擬合[3]，對疫情初期發病病例數進行預測，指出2020年1月1日至15日間武漢公布病例數存在漏報可能。Zhao等基于2020年1月10日至1月24日的公開數據進行指數增長趨勢曲線擬合，由此判斷新型冠狀病毒早期傳播能力接近或略高于SARS[4]。

利用網絡公開數據，筆者分別利用全國累計確診病例數前20天和前30天數據進行曲線擬合：

Y=b1/(1+exp(-b2×(X-b3)))

擬合效果如圖1所示。根據擬合曲線(A)和(B)，全國累計確診病例數均呈指數上升，用前20天數據(圖1(A))預測峰值在2萬以下，而用前30天數據(圖1(B))預測峰值為5萬。事實上，截至2月14日24時，全國已有累計報告確診病例66492例。(http：//www.nhc.gov.cn/xcs/yqtb/202002/50994e4df10c49c199ce6db07e196b61.shtml)。可見，本方法對于已經發生的數據進行擬合，效果非常好，決定系數R2均大于90%。但其預測效果嚴重偏低。

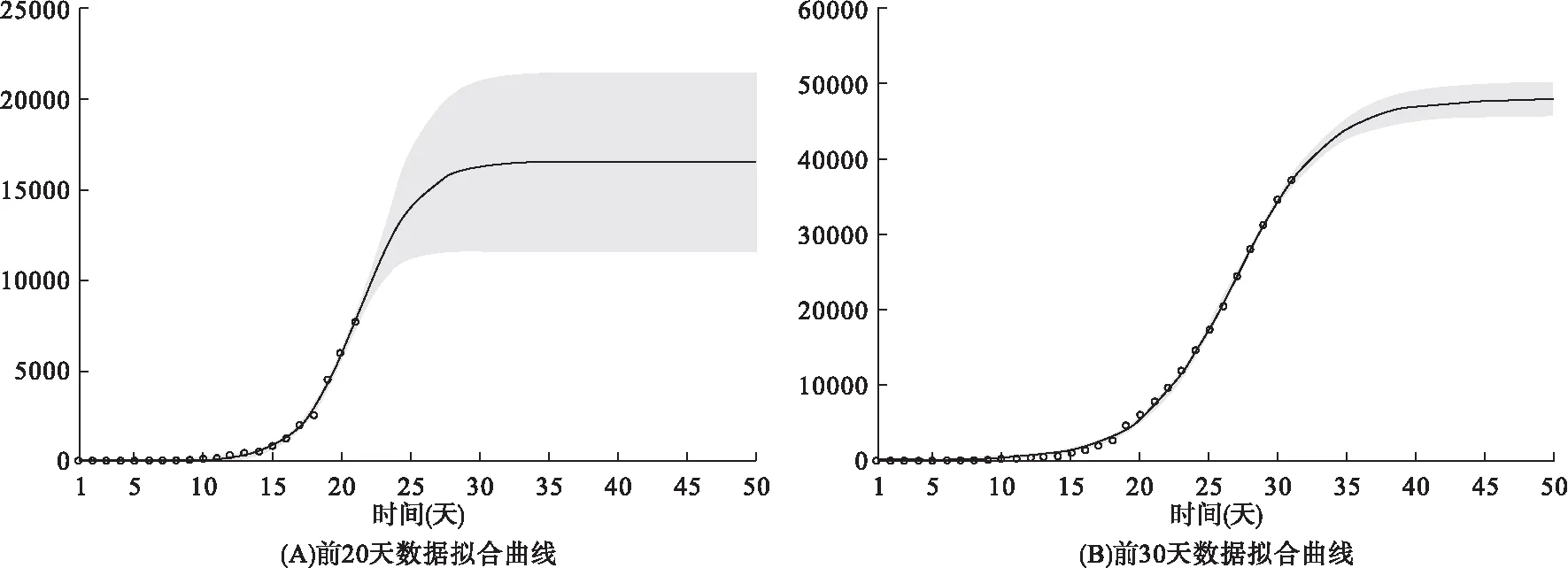
圖1 新型冠狀病毒肺炎疫情曲線擬合

傳染病動力學模型

動力學模型是傳染病的基本數學模型，研究傳染病的傳播速度、空間范圍、傳播途徑、動力學機理等問題。早在1760年，數據家D.Bernoulli就曾用數學模型研究天花的傳播[5]。首次用傳染病動力學模型研究傳染病始于20世紀，1906年Hamer用離散模型研究了麻疹的反復流行[6]。1911年，Ross利用微分方程(ordinary differential equations)研究了瘧疾在蚊子和人群間的傳播，并獲得諾貝爾醫學獎[7]。1926年Kermack與McKendrick提出倉室模型(compartment model)[8]，為后續傳染病動力學研究開辟了新的工具，而倉室模型也是本次疫情預測中應用最多的模型。

最基本的倉室模型為易感-發病-移出(susceptible-infective-recovered)模型，簡稱SIR模型，是將某一固定區域內的人群分為三類：易感人群(S)，發病人群(I)和移出人群(R)。該模型不考慮人群的變化，包括出生、死亡、流動，即此地區是一個封閉的環境，總人群是一個常數，不發生變化，任何時刻的三類人群總數不變。本次疫情中，部分學者利用SIR模型預測本次疫情的局部流行趨勢，并據此提出防控建議[9]。

從應用角度出發，在SIR模型基礎上考慮潛伏期，則為拓展的SEIR模型(susceptible-exposed-infective-recovered)。SEIR模型在本次疫情預測中的應用最為廣泛。例如：周濤等國內學者利用SEIR模型對本次疫情的基本再生數R0(basic reproduction number)進行初步預測[10]，其中S代表易感人群，E代表被感染后處于潛伏期的人群，I代表潛伏期之后已具有感染能力的人群，R表示已經因為治愈并獲得免疫、被有效隔離、因病死亡等原因已經不對流行病傳播動力學產生影響的人群。假設一個I態與S態接觸，S態被感染進入潛伏期的概率(感染率)為β，一個處于E態個體單位時間內將以概率γ1轉變為I態；一個I態個體單位時間內將以概率γ2轉變為R態。SEIR傳播過程可用以下4個微分方程進行描述：

其中，S(t)、E(t)、I(t)和R(t)分別表示t時刻處于S、E、I、R的人數。N表示總人數，且N=S(t)+E(t)+I(t)+R(t)。潛伏期和感染期可分別表示為TE=1/γ1和TI=1/γ2，生成時間(generation time)可近似為病例發生序列間隔，即Tg=TE+TI。基于上述模型，基于不同的網絡數據來源，該研究預測新型冠狀病毒肺炎屬于傳染能力中等略偏高的傳染病，在無干預自由傳播的條件下，R0在3左右。

本次疫情中的絕大部分動力學模型都是以SEIR模型為基礎，考慮疾病的流行特征、易感人群人口學特征、防控措施等因素。例如，Wu等學者在SEIR模型的基礎上，考慮了傳染源、春節期間人群遷移進出武漢的情況，對武漢進行疫情趨勢的預測[11]，構建動力學模型：

其中S(t)，E(t)，I(t)和R(t)意義同上，LW，I為國際流出乘客日平均人數，LI，W為國際流入乘客日平均人數，LW，C為國內流出乘客日平均人數，LC，W為國內流入乘客日平均人數，DE和DI分別為潛伏期和感染期參數，R0為基本再生數，z(t)為動物傳染能力(假設市場關閉前為86例/天，關閉后為0)。該模型預測，如果不采取措施，截至2020年1月25日，武漢市可能有多達75800人感染，提前為疫情防控拉響警鈴。

由于新型冠狀病毒的特性，使得本次疫情具有一定的特殊性，例如，存在無癥狀感染者(asymptomatic infected)，潛伏期人群亦具有一定的傳染性等[12]，魏永越等考慮了新型冠狀病毒肺炎的傳播機理、感染譜、隔離措施等，建立SEIR+CAQ傳播動力學模型，并預測2月底全國(除湖北省)確診病例數為1.82(1.74～1.88)萬，湖北省(除武漢市外)確診病例數為2.16(2.13～2.21)萬，武漢市為4.26(4.19～4.34)萬[13]，該模型考慮參數較為全面，預測結果與實際確診病例數較為接近。哈佛大學公共衛生學院學者基于SEIRS(susceptible-exposed-infectious- recovered- susceptible)模型，在假設各國能夠成功控制本次疫情大流行的前提下，預測在未來更長一段時間的疫情爆發情況，模擬結果顯示在短暫壓制病毒后，如果感染者痊愈后無法獲得長久的免疫力，新冠疫情將卷土重來，在未來的5年內每年如約而至[14]。

另外，隨著疫情防控措施的全面實施，疫情后期通過比較理論預測數與實際發病數，SEIR模型也被用于各項防控措施效果的評價，Wang等估計武漢市自1月23日起嚴格的交通管制使得病例數減少了94.5%[15]，魏永越等通過SEIR+Q模型科學評估防控效果，指出2月12日之后臨床診斷標準的實施及全城拉網式排查等綜合防控措施，使得武漢疫情提前74天結束[16]。

構建傳染病動力學模型時，如能根據疫情實際情況考慮更多參數，模型將更加完善，但考慮的情況越多，模型愈復雜，參數的求解亦愈加困難，馬爾科夫鏈蒙特卡洛(MCMC)等計算機模擬算法成為了常用的求解工具。

人工智能

近年來，得益于人工智能技術的突破性進展以及數據來源的不斷豐富和積累，人工智能不斷運用在新的產業中，其中在醫療領域的應用尤其受到重視和關注。2008年，Google公司開發了“谷歌流感趨勢”(google flu trends，GFT)軟件，利用Google巨大的用戶搜索數據，提前1～2周準確預測了美國流感樣病例比例的變化趨勢[17]。2011年Signorini等以美國境內發表的含有流感相關關鍵詞的美國Twitter量的占比作為預測因子，采用支持向量機回歸(support vector regression，SVR)算法建立了全美及某一地區的流感樣病例比例的實時跟蹤預測模型[18]。我國科學家應用自適應AI模型和多源數據預測重慶市流感活動水平，未來一周流感活動水平預測準確率保持在90%以上，是我國第一個基于人工智能和大數據的流感活動水平實時預測模型[19]。

本次疫情發生以來，大數據、AI等技術的價值在這場全民抗擊疫情的戰役中同樣得到充分展現。其優勢在于可根據疫情發展不同階段、不同地區政府管控力度差異等對基礎模型進行細化和改良，然后代入歷史數據利用機器學習等AI算法對各項參數進行學習訓練，最終得出疫情發展的智能預測模型，并可以根據最新數據不斷演化、優化，提供實時預測。Yang等[20]報道了基于長短期記憶(long-short-term-memory，LSTM)的時間遞歸神經網絡預測模型，模型利用2003年SARS數據進行了AI算法訓練，該模型預測本次疫情將在2月底達到高峰，并通過機器學習算法展示如取消湖北省的交通封閉措施，將導致湖北省在3月中旬出現第二次高峰。Hu等采用改進的自編碼(modified autoencoders，MAE)人工智能方法實時預測100多個國家的新增確診病例數及累計病例數，為防治過程提供決策支持[21]。

總結與討論

新型冠狀病毒肺炎疫情發生以來，疫情未來趨勢的預測一直是學術界和民間關注的熱點。一個好的預測模型，能夠模擬傳染病流行趨勢，量化傳染病的傳播速度，預測時間、空間范圍，評價各種隔離預防措施對控制疾病流行的作用，無疑將為決策部門權衡利弊提供寶貴信息。

傳染病資料不同于一般的醫學資料，患者間是相互傳染的，即個體之間存在高度的相依性，即非獨立的(non-independent)，因而，大部分基于獨立性假設的傳統統計學方法不再適用。例如：曲線回歸，線性回歸等，其基本假設均為個體間是獨立的，若用于傳染病發病數的預測，方差的估計顯然是偏低的。此外，傳統的曲線擬合是完全基于數據趨勢進行預測，無法考慮傳染病的傳播速度、傳播模式及各種防控措施的實施等動態信息，預測效果并不可靠。傳染病資料的分析及預測需要特殊的方法，是方法學研究的一個重要領域[22-25]。

倉室模型分為確定性模型和隨機模型，前者模型中參數假設為固定的；后者模型中部分參數是隨機的，而部分參數是固定的[26]。事實上，很多參數應該設定為隨機的，例如：每個人隨機接觸的人數、潛伏期、康復時間等，這些參數顯然不固定，具有一定的分布規律。有些參數隨著時間的推移在發生變化，例如，不同流行期干預措施的不同，隨著對疾病認識的提高和對疾病的治療不斷完善，出現治愈率提高死亡率下降。在現實防控工作中，首先要根據實際情況，盡可能將參數設定考慮全面，并且需要根據疫情發展和防控策略的改變，動態調整參數，不斷更新動力學模型，也可能獲得短期的、良好的預測效果。

基于AI的預測模型，大都在經典動力學模型的基礎上，利用AI算法對模型的參數進行學習訓練，從而得到根據最新實時發布數據不斷演化的智能預測模型，但AI預測模型的效果同樣取決于設定參數是否合理，也可能受制于AI算法的訓練效果，其預測效果(尤其是遠期預測效果)還有待進一步的考驗。

筆者對本次疫情發生以來所發表的預測模型進行了簡單匯總，詳見表1。正式發表或在公共學術平臺預發表(包括bioRxiv，medRxiv)的模型絕大多數為傳染病動力學模型，尤其是SEIR模型及其擴展，但建模參數、建模數據各不相同，針對的疫情階段也不同，因而對于拐點、累計感染人數及R0等的預測結果相差甚遠。總體看來，本次疫情的預測模型十分豐富，但預測效果卻不盡人意，其主要原因在于：(1)疫情初期對新發傳染病的認識有限，例如未明確潛伏期傳染性的問題，無法納入防控參數；(2)實際防控措施十分復雜，難以量化，例如：對密切接觸者的隔離方式由家庭式隔離轉為集中式隔離將降低傳染風險，但防控物資不足、自我隔離不完全時傳染風險則會增加；(3)診療方案的不斷變化，隨著對新發傳染病認識的不斷提高，國家衛生健康委員會、國家中醫藥管理局聯合發布7個版本“新型冠狀病毒感染的肺炎診療方案”，對疾病的診斷標準不斷變化和完善，使得確診病人定義發生變化，住院收治人數越來越多，治愈率不斷升高；(4)病毒的變異，病毒的基因組在繁殖過程中不斷突變，毒性可能發生變化，傳播能力也將隨之改變。

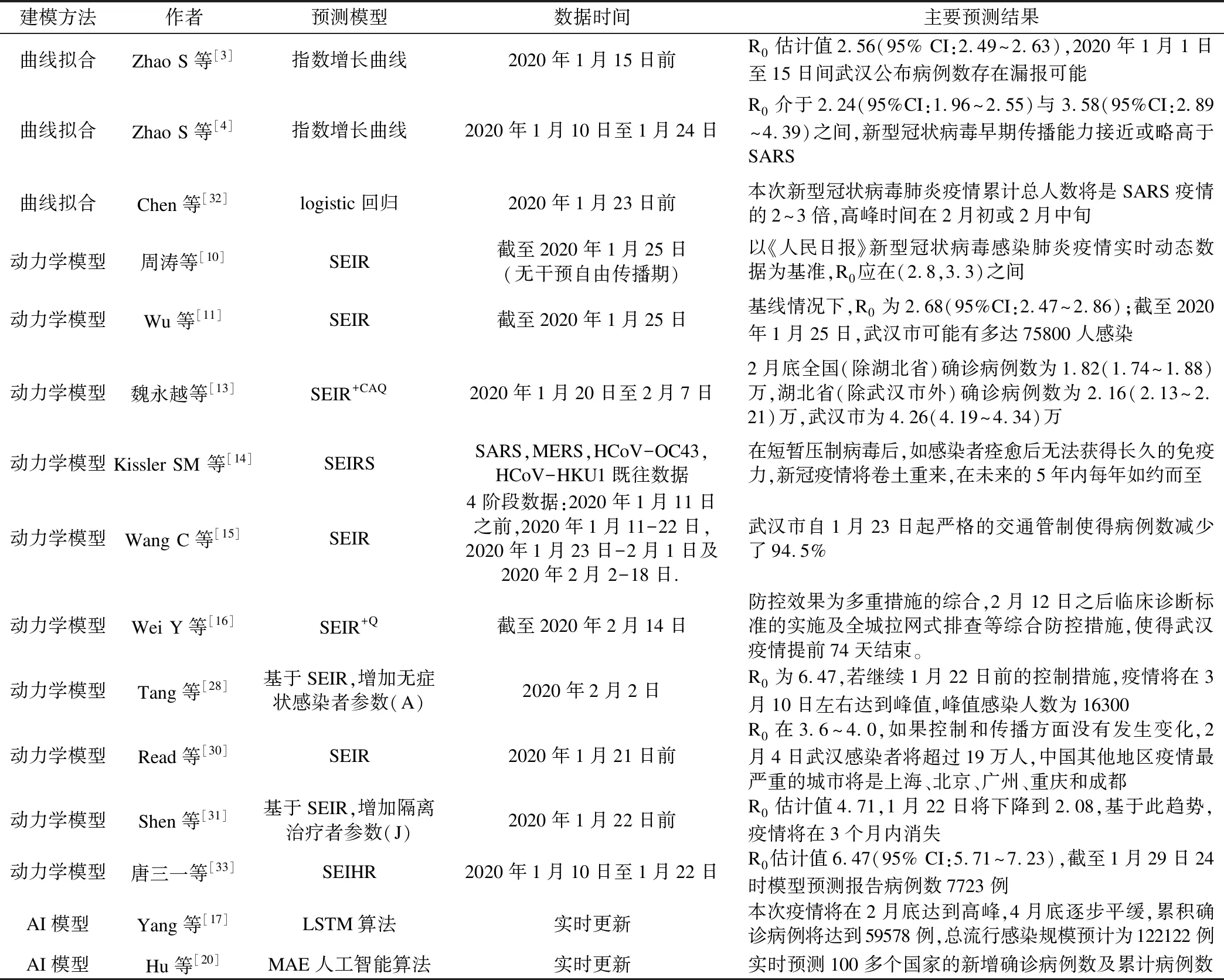
表1 新型冠狀病毒肺炎疫情預測模型匯總

雖然本次疫情中傳染病動力學的預測表現差強人意，但其重要價值在于疾病的早期預警、決策過程的理論支持，以及后續的階段性防控效果和最終防控效果的評估，定量評估防控措施對阻斷病毒傳播、保障人類健康所帶來的效果[27-28]。

由于對新發傳染病了解有限，加上社會環境迅速變化以及各種干預措施影響的不確定性等，及時、準確、可靠地預測正在發生的傳染病流行趨勢是一項巨大挑戰。預測模型不僅需要優質數據，更需要不斷地根據各種環境變化、干預措施的變化，適時調正模型參數，才能準確預測。筆者認為，在綜合利用動力學模型優勢的基礎上，盡可能多地考慮不同影響因素，利用仿真模型構建相應的動態、實時模擬系統，將是一個新的發展趨勢，不僅能在疫情發生時為決策部門提供科學信息，而且有助于日常傳染病防控演練乃至疾病控制體系建設，為國家新型傳染病防控工作保駕護航，意義深遠！