重疊加權法在醫學研究混雜因素控制中的應用*

海軍軍醫大學衛生勤務學系軍隊衛生統計學教研室(200433) 秦宇辰 郭 威 阮一鳴 吳 騁 賀 佳

【提 要】 目的 介紹重疊加權方法的基本原理、方法特性、相對優劣勢及具體實現方法并將其應用于真實世界中比較兩種冠脈支架植入對患者住院時間的影響。方法 以逆概率加權方法為參照，介紹重疊加權方法的原理、實現方法、目標人群，對比分析兩者異同點及相對優劣勢，評估其應用價值。結果 相較于逆概率加權，重疊加權具有諸如簡便易行、不易產生極端權重、最小漸進方差、協變量精確均衡、高檢驗效能、目標人群明確有意義且更易準確估計處理效應等優點，其方法優勢在實例應用中充分展現。結論 重疊加權具有良好方法學特性及廣闊應用前景，可幫助觀察性研究更好實現其處理效應發現職能并為實證研究提供可靠線索，值得在醫學研究中廣泛應用。

傾向性評分法越來越多地被應用于醫療衛生領域，用于控制觀察性數據中的已知混雜因素，實現類似于“隨機化”的效果[1]。而傾向性評分法中的加權方法也因原理易懂、結果易讀、運算迅速等優點被廣泛應用到實踐中。但傳統的加權方法，例如目前常用的逆概率加權方法，易出現極端值，且難以有效處理。Li[2]等人新近提出的重疊加權法(overlap weighting)可以很好克服傳統加權方法的缺點且擁有若干明顯方法學優勢，具有廣闊的應用前景。本文旨在介紹重疊加權的方法原理，對比分析其優劣勢，并在真實世界研究中驗證其方法特性、介紹其實現方法，以期能為該方法在醫療衛生領域中的推廣應用提供參考。

方法原理

Rosenbaum 和 Rubin 于1983年首次提出傾向性評分(propensity score，PS)的概念[3]，其基本原理是將受試者的多個協變量特征綜合表達為一個傾向評分值來表示，分值實際意義為受試者接受處理或者暴露的概率，相似的受試者應具有相似的傾向性分值。而傾向性評分法即是使用傾向評分值進行不同對比組間的分層、匹配或加權等操作以期能實現各協變量在區間均勻分布，由此實現處理效應準確估計[4]。傾向性評分加權方法實質即為基于傾向性評分計算不同類型的均衡權重(balancing weights)，并基于該權重加權構建一個新的虛擬人群，該人群中各類混雜因素獨立于處理組分配，從而實現類似隨機化的效果，保證處理因素效應的準確估計。目前常用的逆概率加權方法(inverse probability weighting，IPW)與本文主要討論的重疊加權最大區別在于使用了不同的均衡權重。逆概率加權基于逆概率權重，而重疊加權使用重疊權重(overlap weights)。為方便讀者理解，我們以逆概率加權為參照，簡要介紹重疊加權的原理、特點及優劣勢。

1.逆概率加權的基本原理

逆概率加權的逆概率權重計算方法及效應估計函數，如下式所示：

(1)

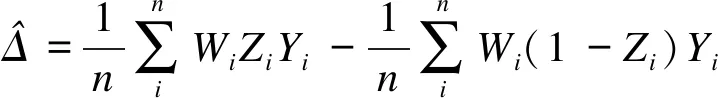
(2)

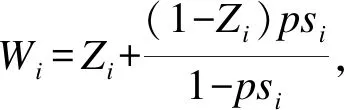
2.重疊加權的原理及方法特點

重疊加權和逆概率加權的效應估計函數一致(如式(2))，但權重計算方法不同。重疊權重的定義方式如式(3)所示：

Wi=Zi(1-psi)+(1-Zi)psi

(3)

由此可見，重疊權重實際為受試者進入其對立組的概率值，取值范圍為(0,1)，傾向性分值趨近于0.5的受試者將被賦予較高的權重而具有極端傾向性分值的受試者將被賦予較小的權重。不同于逆概率加權的目標人群是全人群(ATE)或者處理組人群(ATT)，重疊加權的目標人群是重疊人群，目標效應是重疊人群平均效應(average treatment effect for the overlap population,ATO)。重疊人群是指全人群中對處理組及對照組沒有明顯偏向性(傾向性分值趨近于0.5)，組間人群特征較相似的子人群。雖然與ATE及ATT的可明確識別的目標人群相比，ATO所指向的重疊人群在現實條件下不能明確界定，但該“模糊”人群仍有較大的現實意義：ATO所指的重疊人群受試者無明顯入組傾向，組間受試者特征最相似(重疊度最高)，因此其組間可比性最強、效應估計最可靠，類似于實現了完全隨機化。在臨床實踐中，重疊人群指向的可能即是診療方案尚未達成共識的患病人群，臨床醫生尚不清楚哪種治療方案會使此類人群更受益。因此，此類人群無明顯的入組傾向，也應是研究比較的重點。

此外，相較于其他的加權分析方法，重疊加權有兩點極具優勢的特性。第一，可實現最小漸進方法。Li等人證明了當滿足結局變量方差齊性條件時，重疊加權的漸進方差最小。當然在大多數實際應用情況下，即便結局變量方差齊性條件不滿足(例如二分類結果)最小漸進方差屬性不成立，重疊加權仍可實現較其他加權方法更小的方差；第二，可實現協變量精確均衡。當傾向評分估計模型為基于最大似然估計的logistic回歸時，重疊加權可實現組間所有協變量項(包括主效應、交互項及高次項)精確均衡，其標準化差異趨近于0。因此，重疊加權可以始終實現較其他加權算法更好的協變量均衡性，這也確保了其能始終聚焦于最可比的人群(重疊人群)并實現最準確的效應估計。

3.重疊加權與逆概率加權的優劣勢對比

逆概率加權最大的問題在于對極端權重很敏感，當組間受試者差異較大、特征重疊性較差時很難實現準確效應估計，此時，必須科學消除極端權重，目前常用的方法為極端權重截尾，例如丟棄權重超過閾值的受試者或用閾值替換極端權重，或只加權分析傾向性分值在經驗最優區間[0.1,0.9]內的受試者(具有較好特征重疊性)[6-7]。但這些方法都存在閾值選擇隨意或者可能需要丟棄大量受試者的問題。同時，這些方法也會使估計效應量偏離原先設計的逆概率加權效應量，很難從個體層面定義該效應量所對應的人群。當然，也有研究指出在實際分析中偏離傳統的效應量常見且合理[8]，例如組間重疊性較差時使用傳統效應量會產生大量偏倚，必須采用偏離傳統效應量但能得到較準確效應估計的方法。重疊加權及其對應的ATO就是一個很好的備選。雖然在實際應用中無法從個體層面確定ATO所對應人群，但其所對應的重疊人群有著明確的性質特征，可映射到具有實踐意義的現實人群。重疊權重有界，因此重疊加權不易受極端權重影響，即便組間受試者特征重疊性較差時其仍可較準確估計效應量，此外，其獨具的最小漸進方差及精確均衡特性也保證了其能獲得更準確、更精確的效應估計。雖然精確均衡特性也使傳統的協變量均衡性檢驗方法(如標準化差異等)對重疊加權失效，但可首先使用傳統協變量均衡性檢驗方法基于其他傾向評分分析方法確定最優傾向性評分估計模型再進行重疊加權的思路間接解決此問題。此外，Mao等人的研究發現重疊加權相較于逆概率加權有更高的統計檢驗效能[8]。由上述可知，相較于逆概率加權，重疊加權具有明顯的方法學優勢，也具有更為廣闊的應用前景。

實例分析

1.實例背景

急性心肌梗死患者常需采用經皮冠狀動脈介入術植入冠脈支架再通梗塞血管。傳統的裸金屬冠脈支架易發生支架內再狹窄，而藥物涂層支架可以較好地解決這個問題[9]，因此藥物涂層支架被越來越多地應用于臨床實踐[10]。而不同的冠脈支架植入是否會影響患者的住院時間尚待探究。筆者擬以此問題為例，演示如何基于R軟件的“survey”包實現重疊加權并進行結果解釋。

2.資料概述及分析方法

實例來源于2014年美國住院數據中東北部醫院的住院患者數據[11]，共納入8490條因急性心肌梗死入院并接受兩種冠脈支架植入患者的住院記錄。處理因素為接受裸金屬支架或者接受藥物涂層支架(Treat)，結局為住院時間(LOS，天)，納入患者人口學信息、身體狀況及并發癥信息、醫院特征信息等合計26個協變量。采用標準化差異(SMD)評價加權前后的協變量均衡性，分別使用兩獨立樣本t檢驗、逆概率加權(IPW)及重疊加權(overlap weighing)估計處理因素效應，逆概率加權采用“survery”包默認輸出的穩健標準誤，重疊加權依據Li等人[2]的建議采用bootstrap法估計標準誤。重疊加權的R軟件實現方式請見附錄。

3.結果解釋

圖1展示了加權前后的各協變量的標準化差異，由圖可知，加權前接受金屬冠脈支架和藥物涂層冠脈支架的患者基線情況具有較大差異，各混雜因素在組間分布不均。逆概率加權后，所有協變量的標準化差異均遠低于目前常用的推薦閾值0.1[12-13]，提示加權后的協變量均衡性較好。由于傾向性評分由logistic回歸基于最大似然估計得到，重疊加權如預期的一樣實現了組間各協變量“精確均衡”，標準化差異趨近于0。

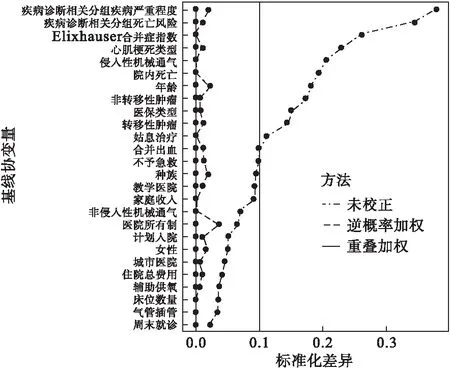
圖1 加權前及加權后兩組患者各基線協變量均衡性情況

如表1所示，三種方法均得出有統計學意義的效應值，即相較于接受藥物涂層冠脈支架的心肌梗死患者，接受金屬冠脈支架患者的住院時間更多。未控制混雜時，處理組比對照組平均多出0.90天的住院時間；采用逆概率加權控制混雜后兩組住院時間差異縮小到0.50天；而采用重疊加權，該差值進一步縮小到0.38天。由于重疊加權所具有的最小漸進方差特點，其取得了較其他方法更小的標準誤及95%置信區間，實現了更精確的效應值估計。綜上可知，相較于接受裸金屬冠脈支架的心肌梗死患者，接受藥物涂層支架雖能獲得有統計學意義的住院時間減少，但客觀減少數較低，實際意義有限。此處需再次特別強調：逆概率加權和重疊加權估計的效應值分別指向兩類不同的人群，前者估計的是ATE指向全人群，后者估計的是ATO指向重疊人群。此點應在分析結果的臨床意義解釋中予以關注。

表1 采用不同種類冠脈支架對住院時間的影響(接受藥物涂層冠脈支架患者為對照組)

#兩獨立樣本t檢驗；*bootstrap標準誤

討 論

傾向性評分方法近年來被越來越多地運用到觀察性醫療衛生數據的分析中，傾向評分加權方法因其簡便易行、計算負荷小、協變量均衡效果好等特點倍受青睞。但其中最常用的逆概率加權法所具有的易受極端權重影響、極端權重處理方法瑕疵較大等缺點也很大程度限制了此類方法的實際應用。而新近提出的重疊加權方法卻能很好地克服這些缺點且擁有極具優勢的方法學特性。該方法可直接推廣到多分類處理組、生存分析、抽樣調查等多種實際應用情境，可方便地與多種模型聯合應用[2,8]，因此具有極為廣闊的應用前景。

需強調的是，重疊加權方法所對應的目標效應量是ATO，該效應量及其所對應的重疊人群也應獲得更廣泛應用及更多關注。重疊人群具有明確、實用、顯著的臨床及公共衛生意義，更重要的是其效應量ATO相較于傳統的ATE、ATT、ATC效應量更易準確估計且具有更高的統計學效能，因此對通過觀察性研究判定某處理因素對特定人群的效應是否為零并以此指導是否進行實證性試驗研究更具意義。此外，需強調的是重疊加權和其他傾向性評分方法一樣，需正確定義傾向性評分模型才可準確估計目標效應量ATO。當然由于其協變量“精確均衡”特點，傳統基于協變量均衡性檢驗判定是否存在傾向性評分模型假定錯誤的方法不再適用，后續研究可聚焦于在重疊加權中判定傾向性評分模型是否存在假定錯誤的方法展開。