定量縱向數據缺失值處理方法的模擬比較研究

陳麗嫦 衡明莉 王 駿 陳平雁△

【提 要】 目的 比較末次觀測結轉法(LOCF)、重復測量的混合效應模型法(MMRM)、多重填補法(MI)在處理縱向缺失數據中的統計性能。方法 以雙臂設計、4次訪視、3種訪視間相關程度為應用背景，采用Monte Carlo模擬技術，產生模擬完整縱向數據后考慮兩種缺失比例和三種缺失機制，即完全隨機缺失(MCAR)、隨機缺失(MAR)和非隨機缺失(MNAR)的缺失數據集。以完整縱向數據的分析結果為基準，評價不同處理方法的統計性能，包括Ⅰ類錯誤、檢驗效能、組間療效差的估計誤差及其95%置信區(qū)間(95%CI)寬度。結果 所有情況下，MMRM和MI均可控制Ⅰ類錯誤，檢驗效能略低于完整數據；LOCF大多難以控制Ⅰ類錯誤，檢驗效能變異較大。多數情況下MMRM和MI的點估計誤差較低，LOCF則表現不穩(wěn)定。所有情況下，MI的95%CI最寬，MMRM次之，LOCF最窄。結論 MCAR和MAR缺失機制下，MMRM與MI的統計性能相當，受各種因素影響較有規(guī)律，可根據實際情況選擇其中一個作為主要分析。LOCF因填補方法的特殊性使得變異較小，精度較高，但其最大的缺陷是不夠穩(wěn)健且不能有效控制I類錯誤，需謹慎使用。基于MNAR缺失機制對缺失數據進行敏感性分析以考察試驗結果的穩(wěn)健性是必要的。

縱向數據在臨床試驗中頗為常見，如對受試者做多個訪視點的重復觀察記錄。縱向數據如果存在缺失值會導致分析結果產生潛在偏倚[1-3]。目前，有關定量縱向數據缺失值的處理方法有多種，但哪種方法更具優(yōu)良特性尚無定論。本研究針對定量縱向數據缺失資料，采用模擬研究方法，考慮完全隨機缺失(missing completely at random，MCAR)、隨機缺失(missing at random，MAR)和非隨機缺失(missing not at random，MNAR)三種不同缺失機制，比較常用的四種缺失數據處理方法，即末次觀測結轉法(last observation carried forward，LOCF)、重復測量的混合效應模型法(mixed model for repeated measurements，MMRM)、基于馬爾可夫鏈蒙特卡羅(Markov chain Monte Carlo，MCMC)的多重填補法和基于線性回歸的多重填補法在縱向缺失數據方面的統計性能。

原理與方法

1.末次觀測結轉法(LOCF)

LOCF屬于單一填補法，是指將最近一次的觀察數據填補缺失值。在所有缺失值填補完成后，形成一個完整的數據集，再按照既定的分析方法進行分析。

2.重復測量的混合效應模型(MMRM)

該方法為一般混合效應回歸模型(general mixed-effects regression model,MRM)的一種特殊形式，由Mallinckrodt 等人在2001年定義[4]。MRM模型如下：

Yi=Xiβ+Ziνi+εi

(1)

其中，Yi為第i個受試者ni×1維反應向量；Xi為ni×p維已知固定效應設計矩陣；β為p×1維未知固定效應參數；Zi為ni×r維已知隨機效應設計矩陣；νi為r×1維隨機效應參數，服從N(0,∑v)分布，εi為ni×1維隨機誤差，服從N(0,∑εi)分布。νi和εi相互獨立。故式(1)中，Yi服從均數為Xiβ，方差協方差矩陣為Zi∑vZ′i+∑εi的多元正態(tài)分布。

MMRM模型將組別、訪視時間以及二者的交互作為固定因素，受試者內誤差作為隨機效應。有研究表明，無論方差協方差矩陣的真實情況如何，受試者內誤差采用非結構化(unstructured,UN)的協方差矩陣可以控制Ⅰ類錯誤[5-6]。

3.多重填補

由Rubin[7]提出的多重填補法旨在解決調查研究中無響應的情況，也適用于處理臨床研究的缺失值。該方法通過對每個缺失值填補多次，形成多個完整的數據集，對每個完整數據集按既定的分析方法處理后再使用統一的方法[8]進行合并得出綜合的結論。

(1)馬爾可夫鏈蒙特卡羅(MCMC)[9]

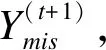
(2)線性回歸法

根據已有觀測數據，建立缺失值與協變量的回歸方程，基于此方程，從參數的后驗預測分布模擬出新的方程用于缺失值的填補。假設Yj是一個含有缺失值的連續(xù)性變量，建立回歸方程

(2)

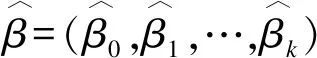
模擬研究

1.完整數據模擬

根據一項治療黃斑水腫，以最后一個訪視點較基線的最佳矯正視力變化值為主要評價指標的雙臂陽性對照臨床試驗結果，設置每組樣本量為160例，包括基線在內有4個訪視點。假設觀測數據服從多元正態(tài)分布。設置四種療效變化模式，所有療效變化模式中，對照組4個訪視點均數為(57,57,60,62)。E0：兩組各時間點的總體均數相同；E00：兩組總體均數在第1和第4次訪視相同，在第2和第3次訪視不同，試驗組4個訪視點均數為(57,58,61,62)；E1：總體均數兩組基線相同，試驗組后3次訪視比對照組大，試驗組4個訪視點均數為(57,62,63,66)；E11：總體均數兩組基線相同，試驗組在第2和第3次訪視稍大于對照組，在第4個訪視點較對照組有更大的提高，試驗組4個訪視點均數為(57,58,61,66)。上述4種療效變化模式中兩組的方差均相同，4個訪視點的方差為(100,110,130,130)；其相應的相關陣如下：

其中C1、C2和C3分別代表各訪視點評價指標具有低、中和高相關性。運用SAS 9.4對以上12種組合各模擬生成2000個完整數據集。

2.缺失數據的構造

根據三種缺失機制(MCAR、MAR、MNAR)，通過隨機刪除完整數據中的部分數據構造缺失數據。設定每個受試者均有基線后第一次測量，即僅可能在第3次和/或第4次訪視出現缺失值。缺失模式為單調缺失，即本次缺失后，往后訪視的數據一并缺失。

MCAR缺失機制下，假設每個訪視點的缺失獨立服從概率為p的二項分布。

MAR缺失機制下，假設某一訪視數據的缺失與缺失前一次的觀測結果有關，即

logit(p(yi=missing|y0,y1,…,yi-1))=a+byi-1

(3)

MNAR缺失機制下，假設某一訪視數據的缺失與本次測試結果有關，即

logit(p(yi=missing|y0,y1,…,yi-1))=a+byi

(4)

設定的缺失機制參數見表1，試驗組約有10%～26%的缺失比例，對照組約有20%～26%的缺失比例，試驗組缺失比例均比對照組低。若兩組缺失機制參數設定相同，則缺失比例接近，相差約為0%～5%；若兩組缺失機制參數設定不同，兩組相差10%～15%。

表1 缺失機制參數設定*

*：p代表二項分布的概率，a和b代表函數(3)、(4)的截距和斜率參數。

綜上，每個完整數據集均對應構造18種缺失數據集，即三種缺失機制(用M1、M2、M3表示)、三種相關陣(C1、C2、C3)和兩種缺失比例(用D0和D1分別表示相近和相差較大)。

3.缺失值處理方法

分別采用LOCF、MMRM、MCMC多重填補和回歸多重填補，對構造的缺失數據進行分析處理。LOCF填補后，將基線觀測值作為協變量進行協方差分析，比較兩組主要評價指標是否存在統計學差異。MMRM模型納入基線觀測值、組別、訪視點、訪視點和組別的交互作用作為固定效應，受試者內誤差作為隨機效應(采用非結構協方差矩陣)。MCMC和回歸法均進行5次填補，對填補后的數據進行協方差分析。本次研究還將對完整數據進行協方差分析，以作為各方法比較的基準。

4.評價指標

評價指標包括Ⅰ類錯誤、檢驗效能，組間療效的估計誤差及其95%置信區(qū)間寬度。

結 果

1.Ⅰ類錯誤和檢驗效能

如圖1所示，在所有設定情況中，MMRM以及多重填補法(MCMC、回歸法)均可控制Ⅰ類錯誤且變化平穩(wěn)。LOCF表現不穩(wěn)定，多數情況下難以控制Ⅰ類錯誤。

在所有設定情況中，MMRM的檢驗效能略高于多重填補法(MCMC、回歸法)，但MMRM以及多重填補法的檢驗效能均低于完整數據，其變化趨勢根據不同的相關系數矩陣和缺失比例情況與完整數據的變化基本相同。隨著相關系數的增加，檢驗效能增大，兩組缺失比例差異的擴大將降低檢驗效能。LOCF在E1模式下的所有設定情況下，檢驗效能略高于完整數據，E11模式下表現不穩(wěn)定，近一半情況下與完整數據相近，另一半情況下與MMRM和多重填補法相當。

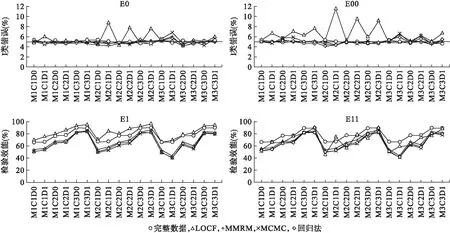
圖1 四種處理方法各種情況下的Ⅰ類錯誤及檢驗效能**：M1、M2、M3分別代表完全隨機缺失、隨機缺失、非隨機缺失；C1、C2、C3分別代表三種相關系數矩陣；D0代表兩組缺失機制參數設置相同，缺失比例接近，D1表示兩組缺失機制參數設置不同，缺失比例相差較大(下同)。

2.組間療效差的估計誤差

組間療效差的估計誤差如圖2所示，在MCAR和MAR缺失機制下，多重填補法(MCMC、回歸法)的估計誤差較小，在0附近波動；MMRM與多重填補法相近，但在部分MAR缺失機制下估計誤差稍大，會低估組間療效。療效變化模式、訪視點間相關性和兩組缺失比例對MMRM和多重填補法幾乎沒有影響。LOCF在MCAR和MAR缺失機制下的估計誤差較大且不穩(wěn)定，受療效變化模式的影響較大，在E11療效變化模式會高估療效，其余模式下低估療效；多數情況下，各訪視點之間的相關性減小和/或兩組缺失比例差距的增加會增大估計誤差。

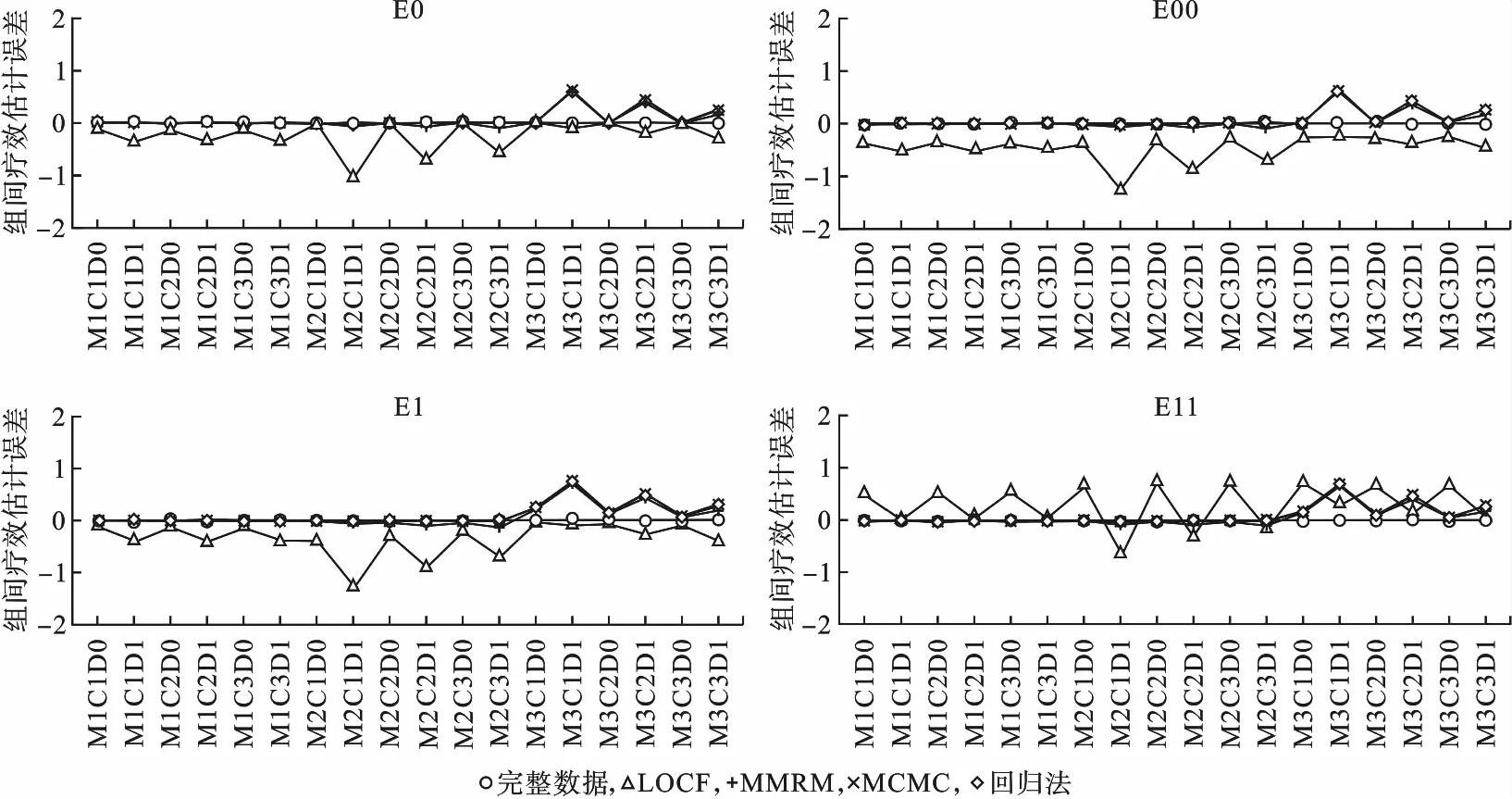
圖2 四種處理方法各種情況下的組間療效估計誤差

在MNAR缺失機制下，MMRM和多重填補法表現一致，估計誤差隨著各訪視點相關性的增加以及兩組缺失比例的接近而減少。如果兩組的缺失比例接近，多數情況下，MMRM和多重填補法的估計誤差最小。療效變化模式對MMRM和多重填補法幾乎沒有影響。LOCF受到療效變化模式的影響較大，在E11療效變化模式下出現高估組間差異以及兩組缺失比例的增大反而降低組間療效估計誤差的情況。訪視點間相關性對其影響不大。

3.組間療效差估計的95%置信區(qū)間寬度

組間療效差估計的95%置信區(qū)間寬度如圖3所示，所有情況下，多重填補法的95%置信區(qū)間寬度最大，MMRM次之但與其相近，LOCF最窄。95%置信區(qū)間寬度均隨著相關系數的增強而變窄，缺失機制對其影響不大。MMRM和多重填補法兩種方法中，缺失比例差異的增加降低了兩組療效差值的95%置信區(qū)間寬度。

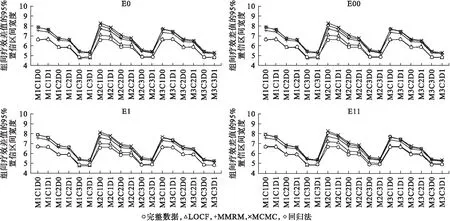
圖3 四種處理方法各種情況下的組間療效的95%置信區(qū)間寬度

討 論

本文共設定四種療效變化模式，每種變化模式下根據三種缺失機制、三種各訪視點療效相關系數和兩種兩組缺失比例情況設定18種缺失數據集，對每種情形的三種缺失機制分別采用四種缺失值處理方法(LOCF、MMRM、MCMC、多重填補的回歸法)進行處理分析。

LOCF法簡單、容易理解，但多數情況下，Ⅰ類錯誤難以控制，檢驗效能和估計誤差表現不穩(wěn)定，MAR和MNAR缺失機制增加其不穩(wěn)定性。訪視點之間相關系數的變化和兩組缺失比例變化相較于MMRM和多重填補法沒有固定規(guī)律的影響。這可能因為LOCF受到療效變化模式影響更大，療效變化越不穩(wěn)定，估計誤差越大(因LOCF假設缺失值的填補值為最后一次觀測值的概率為100%，該假設同時降低了估計的變異)。多項研究也表明，LOCF方法不夠穩(wěn)健，降低了估計的變異，并不總是保守的[10-13]。在使用該方法時，需注意其前提假設的合理性，謹慎使用其作為主要分析。

MMRM的處理方法無需對缺失數據進行填補，納入所有觀測的數據建模進行分析，符合意向性原則，本方法在MCAR和MAR機制下各項統計性能優(yōu)異、穩(wěn)定，在Ⅰ類錯誤、檢驗效能及置信區(qū)間寬度上表現優(yōu)于多重填補，亦有研究表明該方法統計性能優(yōu)于多重填補[14]。該方法對缺失機制的假設為MAR，相關系數越大和兩組缺失比例差異越小，估計誤差越小；相關系數越大和兩組缺失比例差異越大，置信區(qū)間寬度越窄；療效變化模式對其影響較小。根據模擬的結果，仍需注意以下兩點：(1) 由于MMRM中納入了各種固定效應、組別和訪視的交互效應，組別效應的統計檢驗并不與所關注的最后一個訪視點的點估計及其置信區(qū)間完全一致，反而受療效變化模式影響較大。(2) MNAR缺失機制下，估計誤差將增加，應使用其他方法對偏離MAR缺失機制假設的情況進行敏感性分析。

多重填補法對一個缺失數據填補多次，相較于其他方法考慮了填補數據的變異，缺失機制假設為MAR。本研究考察的MCMC和回歸法統計性能相近。考慮多重填補的方法置信區(qū)間最寬，變異程度的增加可能使得其在MAR缺失機制下，估計誤差略小于MMRM。有研究指出多重填補法高估變異程度[15]，填補和分析之間存在沖突[16]。在本研究中，多重填補法和MMRM性能相當，可根據實際情況選擇其中一個作為主要分析，另一個作為敏感性分析。需要注意缺失機制對各種方法的影響，建議采用基于MNAR缺失機制下的其他分析方法，探索試驗結果的穩(wěn)健性。

本研究雖然探索了四種方法在處理合計72種情形的效果，但療效變化模式、相關系數矩陣、各組缺失比例等參數設定并不能涵蓋所有的可能組合。本研究也未考慮具體的比較類型(如非劣和等效性)，故本研究結論具有一定的局限性。