基于EGARCH模型的煙臺市人群死亡率波動非對稱效應分析及預測應用

煙臺市疾病預防控制中心(264003) 劉海韻 張紅杰 陳遠銀 于紹軼 曲淑娜 王倩倩 徐 穎 王茂波

【提 要】 目的 揭示人口及非人口影響因素對煙臺市人群死亡率波動的非對稱效應，預測死亡率變化趨勢。方法 以2007-2017年全市死亡數據作為樣本數據，建立季節調整月度死亡率ARIMA-GARCH時間序列模型，繪制信息沖擊曲線，預測2018年死亡率。結果 在偏正態分布假設下擬合的ARIMA(1，1，1)(1，1，0)12-EGARCH(1，2)模型較好地捕捉到死亡率波動性，且預測效果優于單純ARIMA模型。結論 煙臺市人群死亡率的波動對人口因素的影響較非人口因素更加敏感，模型的短期預測結果可對死亡率的變化趨勢起到一定的指示作用。

死亡率變化同人口因素及非人口因素密切相關[1]。目前國內相關研究主要采用死亡率差別分解法[2]定量分析人口和非人口因素對死亡率變化的影響，但該法只能計算兩大類因素對起始年和終末年死亡率差異的貢獻和比例，無法表達其在死亡率變化過程中引起的死亡率波動。本文以煙臺市人群月度死亡率作為子年度數據樣本建立ARIMA-EGARCH組合時間序列模型，獲取信息沖擊不對稱曲線，在死亡率差別分解定量分析的基礎上，直觀揭示人口及非人口因素給死亡率波動帶來的非對稱效應。

資料與方法

1.資料來源

2007-2009年常住人口數據和死亡數據來源于2009年煙臺市死因回顧性調查[3]，2010-2018年死亡數據來源于煙臺市死因網絡登記報告。人口數據來自煙臺市公安局，標準人口采用中國2000年第5次人口普查數據。

2.方法

(1)總體死亡狀況

分別計算2007-2018年粗死亡率、年齡標化死亡率和月度死亡率，月度死亡率由每月死亡數除以當年人口數求得；采用Joinpoint模型計算粗死亡率和標化死亡率的平均年度變化百分比(average annual percent change，AAPC)及其95%可信區間；采用直線回歸評價月度死亡率的總體趨勢。

(2)死亡率差別分解

對死亡率差別的影響因素進行定量分解，解釋死亡率的上升或下降在多大比例上是由人口或非人口因素作用的。其中，人口因素主要是指人口年齡結構老齡化因素[4]；非人口因素統稱為非人口年齡結構因素，具體是指除人口因素外的所有影響死亡率變化的因素總和，主要包括社會經濟因素、醫療衛生服務因素、環境因素和人群行為因素等[2]。計算公式為：

其中，Cu為終末年年齡組人口構成，C0為起始年年齡組人口構成，Ru為終末年年齡組死亡率，R0為起始年年齡組死亡率；由貢獻值判斷人口因素與非人口因素對死亡率的作用方向。

(3)時間序列分解

采用加法模型對月度死亡率進行分解，從中剔除季節變動項，形成季節調整月度死亡率用以滿足后續建模分析和預測的需求。模型公式為：Yt=Tt+St+It。其中，Yt表示原始時間序列，Tt表示長期趨勢項，St表示季節變動項，It表示隨機干擾項。

(4)EGARCH(esponential generalized autoregressive conditional heteroskedasticity)建模流程

傳統計量模型無法捕捉到死亡率的異常波動[5]，而 GARCH模型在處理數據變異性方面具有獨特優勢，但其對模型參數的要求比較嚴格，且假定了方差具有對稱性。能夠反映非對稱性的GARCH擴展模型有很多，其中EGARCH模型是研究杠桿效應的基準模型。與其他擴展模型相比，EGARCH模型穩定性最好[6]，其主要優勢在于方程系數不受任何限制，能同時表達死亡率的時變方差和非對稱效應，因此本研究選擇該模型進行分析和預測。具體建模流程如下：

①建立季節調整月度死亡率ARIMA模型[7]；②建立不同條件分布假設下的低階(滯后2階以內)EGARCH模型，以最小AIC(Akaike’s information criterion)值為原則篩選模型，采用擬合優度檢驗判斷EGARCH模型標準殘差的實際條件分布與假設分布是否一致，假設分布依次為正態分布(normal distribution，norm)、偏正態分布(skew normal distribution，snorm)、標準學生t分布(student′st-distribution，std)、偏態t分布(skew student′st-distribution，sstd)、廣義誤差分布(generalized error distribution,ged)及帶偏廣義誤差分布(skew generalized error distribution,sged)；③采用指示偏誤檢驗[8]判斷模型捕捉死亡率波動的穩健性與正確性，包括偏誤檢驗(sign bias test，SBT)、正偏誤檢驗(positive size bias test，PSBT)、負偏誤檢驗(negative size bias test，NSBT)和以上三者聯合檢驗(joint test，JT)；最終建立模型公式如下：

條件分布方程：εt=σtηt

條件方差方程：

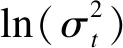
(5)死亡率預測及效果評價

利用2007-2017年月度死亡率數據作為季節調整和建模樣本，提取模型擬合值與真實值進行樣本內擬合效果評價；做出2018年1-12月預測，并與真實值進行樣本外預測效果評價；此外，對未進行季節調整的原始月度死亡率建立ARIMA模型，進行預測效果對比。預測效果評價采用均方根誤差(root mean square error,RMSE)，公式為：

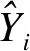
(6)統計軟件

應用Joinpoint Desktop Software(4.7.0.0版本)擬合Joinpoint模型；應用R語言(3.6.0版本)的decompose函數以及forecast包、rugarch包、fUnitRoots包和TSA包編程實現時間序列的分解及模型建立、檢驗和預測。

結 果

1.人口老齡化概況

根據區域人口老齡化程度和速度分類[10]，2018年煙臺市≥65歲人口構成(16.77%)大于14%且小于等于20%，與2007年相比年均變化百分比AAPC=4.88%(95%CI：3.74%～6.04%，P<0.05)大于4%，屬于快速老齡社會型，即本地區人口進入老齡社會階段，并且很快會進入下一個人口老齡化階段。如圖1。

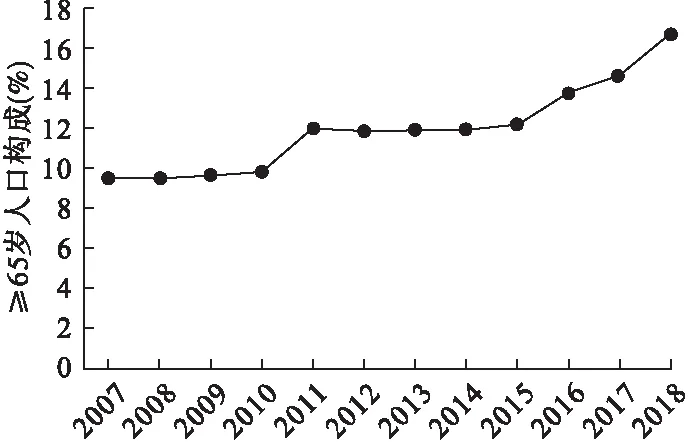
圖1 2007-2018年煙臺市≥65歲人口構成變化趨勢

2.總死亡水平變化趨勢

2007-2018年煙臺市人群粗死亡率總體呈明顯的上升趨勢(AAPC=2.15%，95%CI：1.56%～2.74%，P<0.05)，而標化死亡率總體明顯下降(AAPC=-4.95%，95%CI：-6.20%～3.69%，P<0.05)，如圖2。

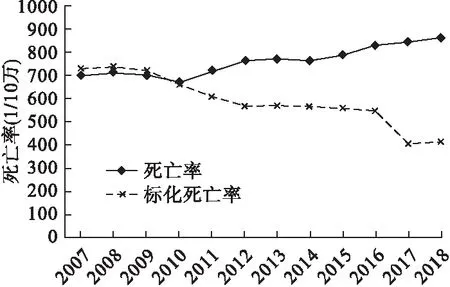
圖2 2007-2018年煙臺市人群粗死亡率及年齡標化死亡率變化趨勢

2007-2018年全市粗死亡率差別分解可得，人口因素導致死亡率上升362.40/10萬，占人口和非人口因素共同作用的65.00%；非人口因素導致死亡率下降195.15/10萬，占35.00%。

3.月度死亡率季節調整

2007-2017年煙臺市原始月度死亡率分布具有明顯的周期性規律；經季節調整后的月度死亡率周期波動幅度較原始序列明顯縮小，隨年度變化總體呈明顯的上升趨勢(F=150.30，P<0.05)，如圖3。

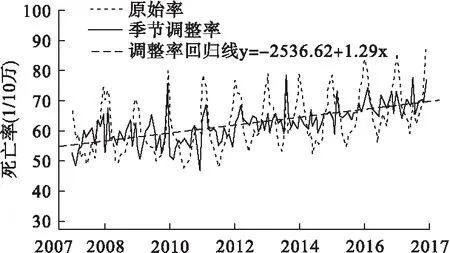
圖3 2007-2017年煙臺市人群季節調整月度死亡率變化及回歸趨勢

4.季節調整月度死亡率ARIMA模型建立

經季節調整月度死亡率的1階差分平穩時間序列自相關函數(autocorrelation function，ACF)和偏自相關函數(partial autocorrelation function，PACF)圖判斷，如圖4，依據AIC值最小原則進行篩選，選定乘積季節ARIMA(1，1，1)(1，1，0)12為最佳模型。

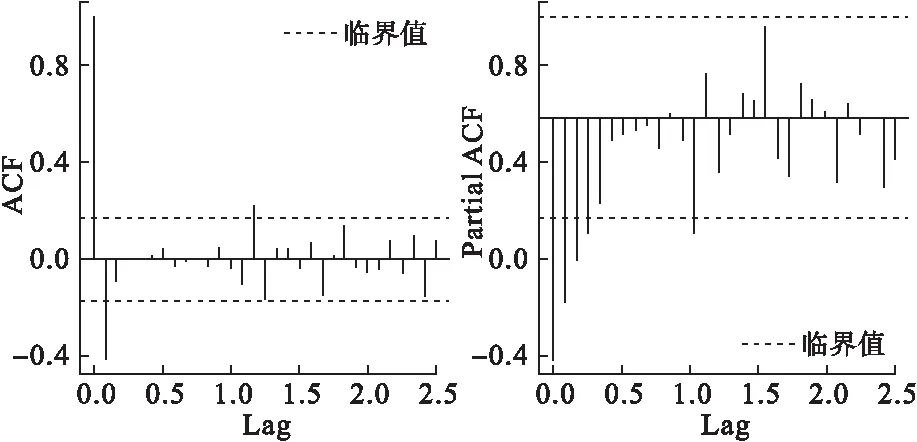
圖4 季節調整死亡率1階差分時間序列的ACF和PACF圖

5.EGARCH模型建立

對不同條件分布假設下的模型進行對比，EGARCH(1，2)-norm和EGARCH(1，2)-snorm模型系數全部呈統計顯著性(P<0.05)，依據AIC值最小原則，選擇EGARCH(1，2)-snorm模型，見表1。擬合優度檢驗顯示，EGARCH(1，2)-snorm模型標準殘差分布假設與真實分布相一致(χ2=61.94，P=0.10>0.05)。

指示偏誤檢驗均不具有統計顯著性(P>0.05)，提示EGARCH(1，2)-snorm模型成功捕捉了死亡率波動的非對稱杠桿效應(表2)。

最終選擇snorm分布的EGARCH(1，2)模型，條件方差方程如下：

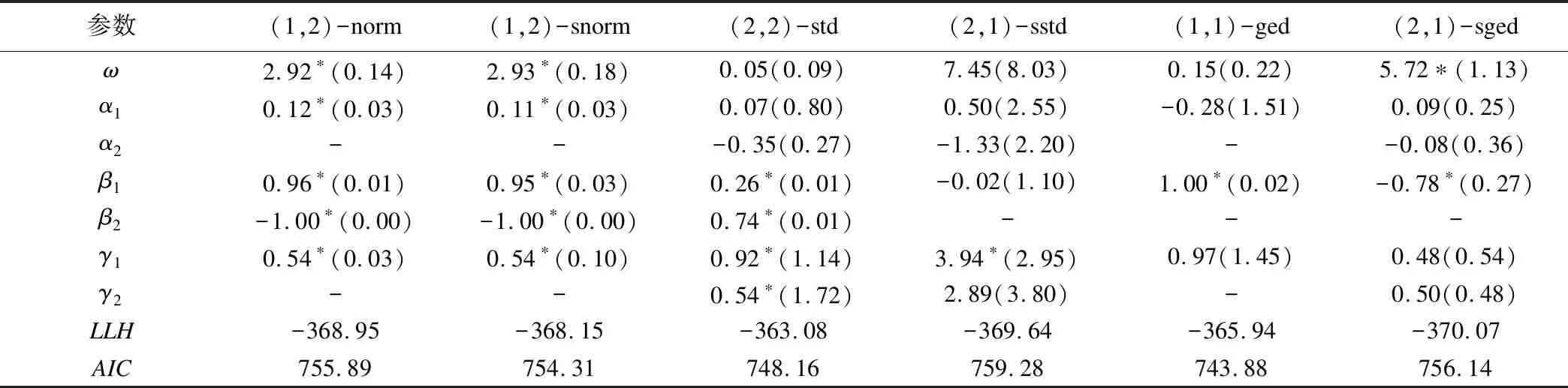
表1 不同分布假設下EGARCH模型系數估值及檢驗結果

*：表示p<0.05；括號內為最大似然結果估計的穩健標準誤；“-”表示不存在。

表2 EGARCH(1，2)-snorm模型指示偏誤檢驗結果

其中，杠桿效應系數γ1=0.54>0，提示外界信息沖擊存在杠桿效應，正面信息比負面信息對波動產生更大影響；死亡率信息沖擊曲線顯示，x軸負軸表示負面信息，正軸表示正面信息，負軸和正軸的曲線走勢不對稱，死亡率在信息沖擊小于0(負面信息)時，曲線下降平緩，受正面信息沖擊時曲線上升陡峭。如圖5。

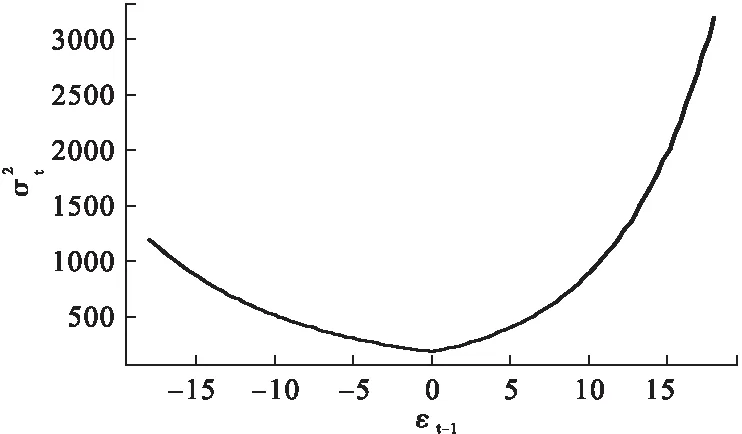
圖5 2007-2017年煙臺市人群季節調整月度死亡率信息沖擊曲線

6.模型預測及評價

RMSE值顯示，ARIMA-EGARCH模型在整個樣本期內RMSE值最小，預測精度最高；季節調整ARIMA模型樣本內擬合效果不及未季節調整ARIMA模型，但樣本外預測效果好于未季節調整ARIMA模型；未季節調整ARIMA模型樣本外預測效果較樣本內預測效果變差，見表3。

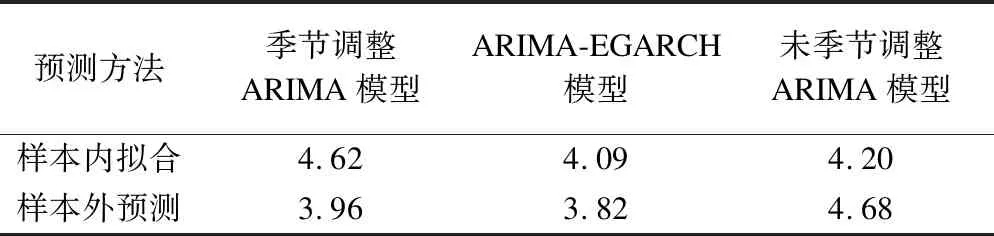
表3 三種模型對煙臺市人群月度死亡率預測的RMSE評價

圖6顯示，利用ARIMA-EGARCH模型做出為期1年的短期預測值與2018年實際值相比，吻合程度較高，周期波動的變化趨勢一致，月度死亡率預測值仍呈震蕩上升趨勢。

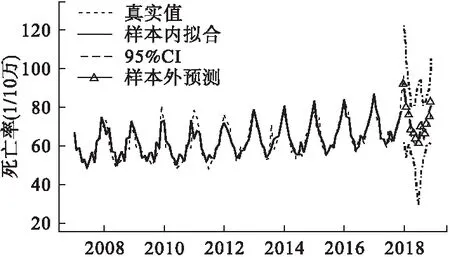
圖6 煙臺市人群月度死亡樣本內擬合與樣本外預測值與實際值對比

討 論

2007-2018年煙臺市人群年齡標化死亡率呈明顯的下降趨勢，且下降幅度遠大于標化前粗死亡率的上升幅度，反映出年齡結構因素對死亡率的明顯影響，死亡率差別分解顯示人口老齡化極大程度掩蓋了非年齡結構因素對人群健康水平起到的積極作用，最終導致了全市死亡率總體上升，這與上海市閔行區死亡率變化分析結果一致[11]。

在建立EGARCH模型時，由于目前對該類模型的定階方法研究還不多，低階模型已能滿足大多數的應用[12]，且擬合程度并不差于，甚至好于高階模型[13]。因此考慮到模型構造的簡潔性，并未嘗試建立其他更高階的EGARCH模型。死亡率的非對稱杠桿效應是指死亡率受到外界正面信息的沖擊與受到同等強度負面信息的沖擊所產生的波動程度會表現出明顯的不同，全市死亡率差別分解顯示老齡化因素為促進死亡率上升的正面信息，非年齡結構因素為負面信息。結合杠桿效應系數γ值和信息沖擊曲線可判斷出，外界信息沖擊產生的死亡率波動存在杠桿效應，全市老齡化因素產生的死亡率波動大于同等強度的非年齡結構因素。換言之，死亡率波動對人口老齡化因素更為敏感，意味著年齡結構上的小變動能轉化為死亡率上的大波動，而同一時期內促進死亡率下降的非年齡結構因素無法抵消老齡化因素對全市死亡率上升的沖擊，若僅通過改善非年齡結構因素來刺激全人群死亡率產生下降的波動將收效甚微。目前，積極推進養老保障體系建設，著力提升老年人群健康，最大程度減緩年齡結構性死亡的消極波動，是改善煙臺市人口死亡率水平的首要路徑。

ARIMA-EGARCH聯合模型的預測效果優于單純ARIMA模型，結合指示偏誤的檢驗結果，反映出模型正確捕捉到了死亡率變化過程中的波動性。另外，雖然季節調整ARIMA模型在樣本內擬合效果不及未季節調整ARIMA模型，但其樣本外預測效果提升，同時未季節調整ARIMA模型樣本外預測效果較樣本內擬合效果變差，反映出季節因素可能會讓預測模型誤判其為不規則變動，從而降低模型的預測精度，體現出以月度死亡率為子年度數據，對其進行時間序列分解并進行相應季節調整的必要性[14]。