垂直軸盤式電機磁浮軸承系統研究*

王晉美，孫京紅，李光華，張鎮驛，朱 軍*

(1.河南理工大學 電氣工程與自動化學院，河南 焦作 454000；2.河南省電子信息產品質量監督檢驗院，河南 鄭州 450002)

0 引 言

由于具有無接觸、無摩擦、損耗小等優點，磁浮軸承常常被應用在風力發電機上，代替傳統的機械軸承，來減少機械軸承帶來的摩擦損耗，提高能量的轉換效率[1-3]。根據磁力的提供方式，磁浮軸承可分為被動式磁軸承、主動式磁軸承以及混合式磁軸承[4-6]。

國內外學者對磁浮軸承的各個方面均展開了研究。美國、瑞士、德國等國家的一些機構對磁浮軸承技術的研究目前處于世界領先地位。國內對磁浮軸承技術的開展較晚，目前還在科研實驗階段，還未有公司有大規模的市場開發。但是國內磁浮技術在磁懸浮列車的運用較為成熟。

磁浮軸承主要應用于高速機床、空氣壓縮機、醫療科學、航空航天等領域。

朱熀秋[7]用等效磁路法對永磁和勵磁混合磁軸承的磁路進行了計算，并用有限元進行了仿真，得出了該電機結構擁有合理緊湊、體積小、效率高等優勢；MARTH E, JUNGMAYR G and AMRHEIN W[8-9]通過對磁浮軸承幾何參數的確定，改變了磁浮軸承充磁方向，提出了新型Halbach結構，提高了軸承剛度；王曉遠[10]應用果蠅算法，對飛輪儲能用徑向磁懸浮軸承進行了優化，提高了軸承承載力、剛度，減小了軸承體積；RAVAUD R[11]運用基于庫林定律的解析法，對軸向磁化的永磁體進行了分析，并將二維解析結果與三維仿真結果進行了對比分析，確定了二維近似的有效范圍。

根據Earnshaw定律，永磁體在無外力的作用下不可能實現6個自由度的懸浮，即需要在至少一個自由度上使用支撐外力。

本文提出一種適用于小型垂直軸盤式風力發電機的新型全懸浮磁軸承系統，其利用徑向三環磁浮軸承保持轉子徑向懸浮，軸向磁浮軸承提供該電機的承載力。

1 盤式電機磁浮系統結構選擇

本文設計了一種由徑向三環磁軸承和軸向磁軸承兩個獨立懸浮單元構成的全懸浮軸承系統，垂直軸風力發電系統如圖1所示。

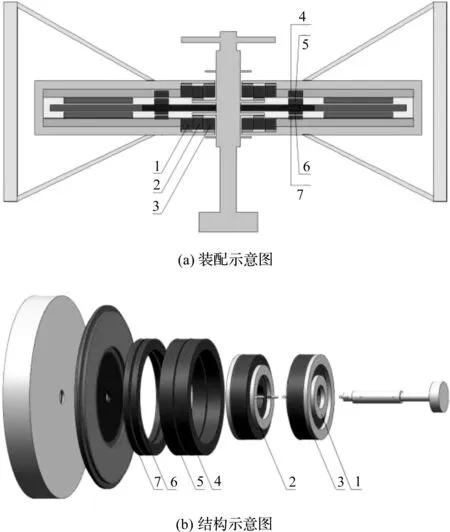
圖1 垂直軸風力發電系統1-外磁環；2-中磁環；3-內磁環；4-上軸向磁環1；5-上軸向磁環2；6-下軸向磁環1；7-下軸向磁環2

小型垂直軸磁懸浮風力發電機具有體積小、結構簡單緊湊、重量輕、發電機轉子直接與風機固定啟動等優點；利用磁懸浮軸承無摩擦、回轉速度高等優點，可提高發電機的能量轉換效率。而主動式與混合式磁浮軸承控制系統結構復雜、占用空間大、所需安裝零件較多，故該系統選用被動式磁浮軸承作為支撐軸承。

由于徑向磁軸承磁路與軸向磁軸承磁路是相互獨立的，即徑向力與軸向力是解耦的，同向充磁的兩相對放置的永磁體，不僅漏磁程度較反向充磁磁體嚴重，且磁路會耦合嚴重，故本文選用的磁浮軸承所用永磁體均為反向充磁磁體，為斥力磁浮軸承。

固定在發電機轉子及主軸兩側的徑向磁軸承，維持發電機轉子的徑向懸浮；上軸向磁環與下軸向磁環位于發電機定子上、下兩側，利用斥力，承擔風力發電機及其組件的重力，使轉子保持軸向懸浮。

2 徑向磁軸承結構設計

筆者在徑向懸浮磁軸承的選擇上，使用型號為N2M的釹鐵硼磁環材料，轉軸、端蓋等采用導磁性材料。

由于雙磁環永磁體構成的磁浮軸承的徑向剛度較小，3個永磁環徑向疊加構成的磁浮軸承的徑向剛度會得到提升[12]。

單對磁環提供的承載力及剛度都比較小，為了增加發電的穩定性，筆者選用多對磁環疊加來提高承載力，增大徑向磁力軸承的徑向剛度。

磁環疊加方式分為軸向疊加與徑向疊加，徑向疊加磁環需要較大空間來增加氣隙的截面積。而該小型垂直軸風力發電機體積小，安裝磁浮軸承空間有限，故筆者在傳統的徑向雙環磁軸承基礎上，采用了一種新型三環磁浮軸承，五層軸向疊加，平行充磁且充磁方向兩兩磁環相對，借以產生極大的斥力，使轉子保持徑向懸浮。

通過分析釹鐵硼材料的抗磁曲線及退磁曲線可知，稀土永磁材料的退磁曲線接近直線，材料矯頑力很高不易退磁，故多塊永磁體疊加的磁場分布可看成是單個磁體磁場分布的線性疊加；結合文獻[13]，可通過計算得到徑向軸承的合適尺寸。

永磁體徑向磁化長度為:

(1)

式中：f—磁阻系數，一般取1.1～1.5；k—空氣中磁路長度等效為氣隙磁路長度的修正系數；Lg—工作氣隙長度，本文取0.5 mm。

承載力是衡量軸承的重要參數，是磁浮軸承在最大允許磁動勢下所得到的懸浮力，大小與磁環結構及充磁方向有關，其計算公式為：

(2)

式中：Bg—氣隙中磁感應強度；Ag—為氣隙的截面積；u0—真空磁導率。

剛度指某種結構抵抗形變的能力[14-15]，是徑向磁力軸承沿某個方向上的單位位移所需的沿該方向系統外界干擾力的增量，其數學表達式為：

(3)

通過計算可得，磁環參數的寬度(w)×高度(h)×氣隙(g)為8 mm×8 mm×0.5 mm；磁環每層高度為1.6 mm。筆者將磁環參數應用到傳統雙環和新型三環中，進行仿真。

根據單位尺寸內產生剛度的大小，可評判磁浮軸承性能的好壞。

磁環剛度對比如圖2所示。

圖2 磁環剛度對比

由圖2可知：相同條件下，新型三環的剛度比傳統雙環的提高了至少2.4倍，且在計算范圍內剛度始終為正值，說明轉子在徑向上可以穩定懸浮。

磁環剛度對比如圖3所示。

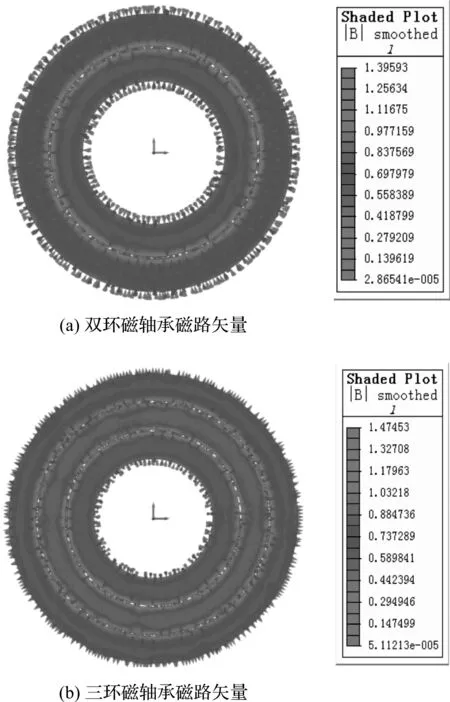
圖3 磁環磁路矢量對比

由圖3可知：新型三環磁密由雙環磁軸承時的1.396 T提高到1.475 T，小于達到磁飽和時的2.0 T，可見三環磁軸承對磁體材料的利用率更高。

綜上所述，筆者選擇新型三環磁軸承作為提供徑向懸浮力的徑向磁浮軸承。

3 軸向磁軸承結構設計

該軸向磁浮軸承的軸向懸浮力由兩部分合成：(1)上軸向磁環間的氣隙產生的磁場斥力；(2)下軸向磁環間的氣隙產生的磁場斥力。

斥力磁軸承基本結構如圖4所示。

圖4 斥力磁軸承基本結構

由圖4可知，利用斥力進行懸浮的磁軸承4種基本結構分別為：軸向疊加斥力磁軸承-垂直向，徑向疊加斥力磁軸承-水平向，徑向疊加斥力磁軸承-垂直向，軸向疊加斥力磁軸承-水平向。

所設計的垂直軸發電機為盤式電機，采用雙轉子單定子結構，需要磁環提供軸向承載力平衡軸向的重力，故有圖4(a，d)所示的軸向疊加結構可供選擇。結構圖4(a)相比于結構圖4(d)更加穩定；結構圖4(d)兩磁環相對的一面均存在兩種極性，一旦兩磁環的徑向偏移超出一定值，該結構就由斥力磁環變為吸力磁環；而圖4(a)兩磁環所對極性為同一極性，所以筆者選擇結構圖4(a)為軸向磁軸承基本結構。

若只設計單對軸向斥力磁環提供承載力平衡重力，當發電機受到大于重力的向上擾動，又在向上斥力的作用下，會使電機上拋情況失控，嚴重時會損壞電機。經綜合考慮，筆者設計一個包含上軸向磁環與下軸向磁環的軸向磁軸承。

上軸向磁環1固定在定子上為靜磁環，上軸向磁環2固定在轉子上為動磁環，動/靜永磁環之間的磁斥力使動磁環在受載時產生一個向上的恢復力F1；下軸向磁環1固定在定子上為靜磁環，下軸向磁環2固定在轉子上為動磁環，動/靜永磁環之間的磁斥力使動磁環在受載時產生一個向下的恢復力F2。這樣在受到向上擾動時，有了方向向下且距離越小力越大的F2存在，平衡了向上的擾動，使電機能夠穩定懸浮。根據受力分析，有：

F1-F2-G=0

(4)

式中：F1—向上的恢復力；F2—向下的恢復力；G—重力。

由上式可知，利用F1與F2之間的差值平衡重力，可實現軸向懸浮。

3.1 上軸向磁環結構設計

該風力發電機及其組件重力共計200 N，上軸向磁環1固定在定子側為靜磁環，上軸向磁環2固定在轉子側為動磁環。

軸向磁軸承承載力如圖5所示。

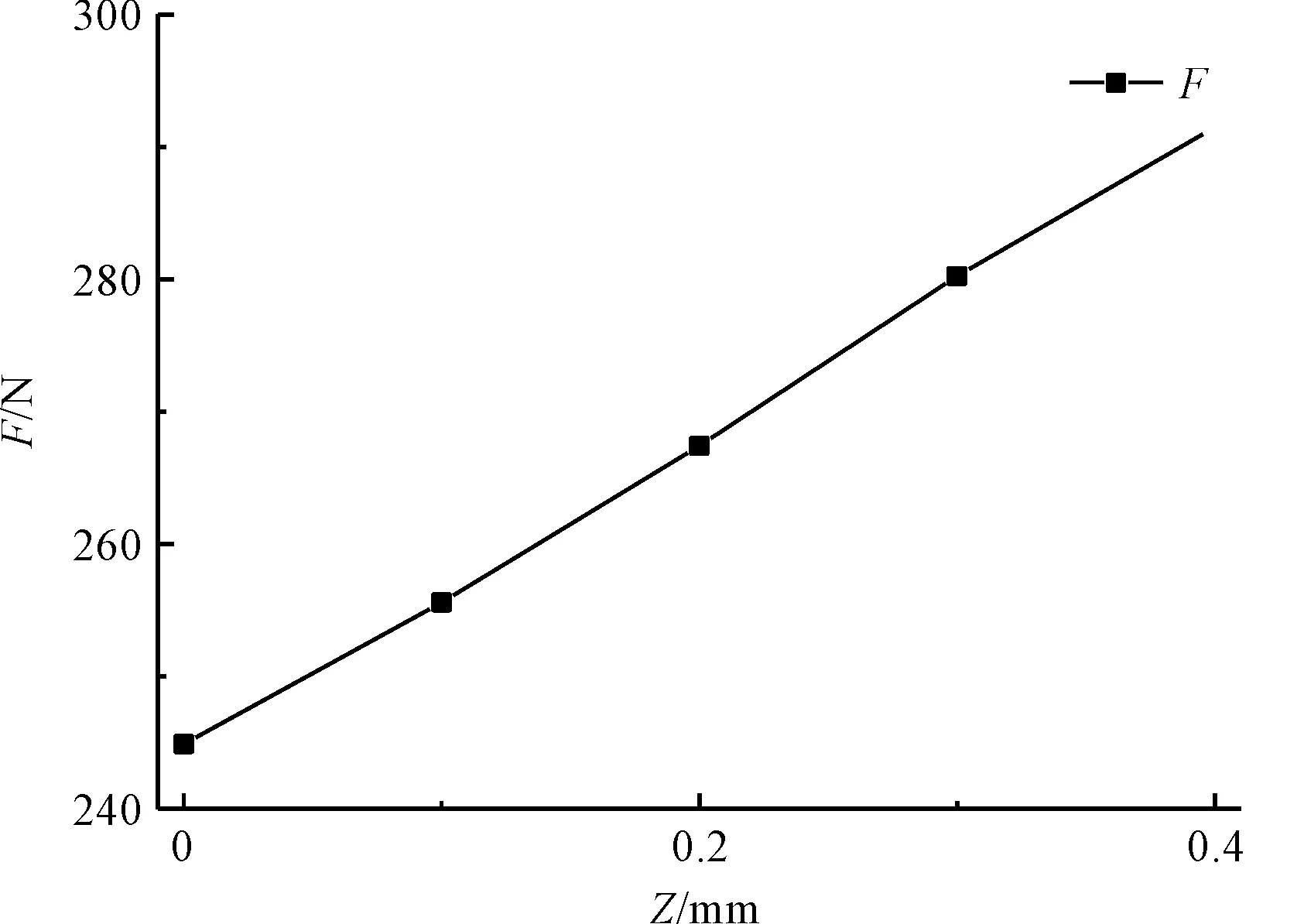
圖5 軸向磁軸承承載力

筆者設定上軸向磁環的原始尺寸，然后進行研究。磁環參數的寬度(w)×高度(h)×氣隙(g)為8 mm×4 mm×0.5 mm。以這組尺寸為基礎，研究磁軸承的性能與尺寸參數變化之間的關系。

筆者以垂直向下方向為位移正方向，對上軸向磁環的承載力進行有限元建模仿真，結果可知，該磁環承載力較小，需要對其進行優化。

3.2 上軸向磁環結構優化

3.2.1 參數變量優化

在磁浮軸承的設計中，上軸向磁環的主要性能指標有承載力、剛度等，其大小取決于磁浮軸承的體積。為得到最理想的承載力、剛度，本文對影響磁環性能的寬度w、高度h、氣隙g在內的多個變量(因子)運用田口法進行優化設計。

以承載力F及剛度K為約束條件(品質特性)，以得到最優結構為目的，各設計變量及影響因子水平取值如表1所示。

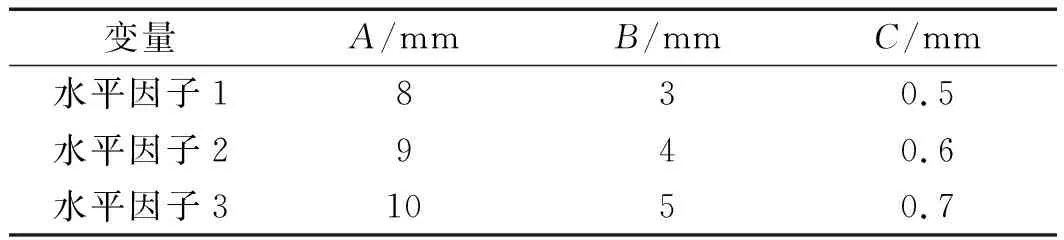
表1 各設計變量及影響因子水平取值

針對以上3個變量的變化范圍，每個優化變量取3個不同的因子水平，最終確定選用L9(33)正交表，只需做9次試驗。

3變量3水平正交表實際值如表2所示。

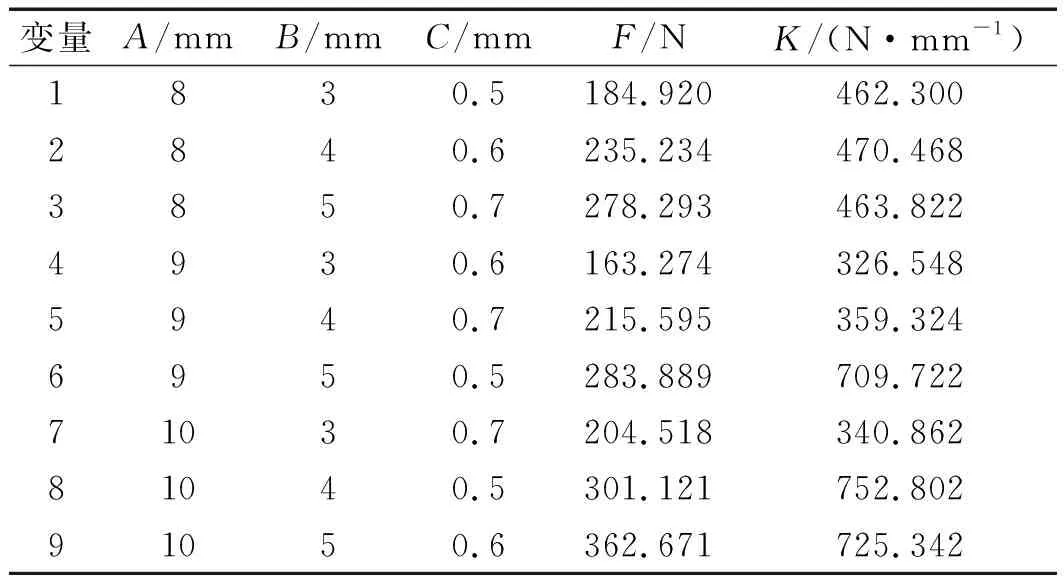
表2 3變量3水平正交表實際值

3.2.2 因子水平對品質特性影響所占的比重

分析不同因子水平對品質特性影響所占比重，如因子B在水平因子3下對F的影響，可以通過下式求解[16]：

(4)

各水平因子對承載力F及剛度K的影響如表(3，4)所示。

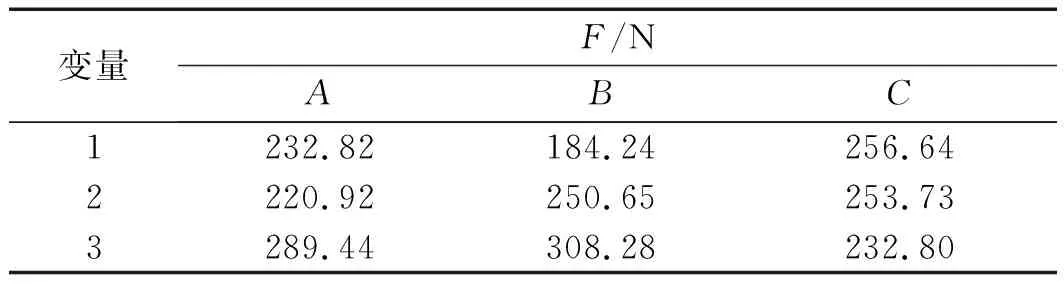
表3 各水平因子對承載力F的影響

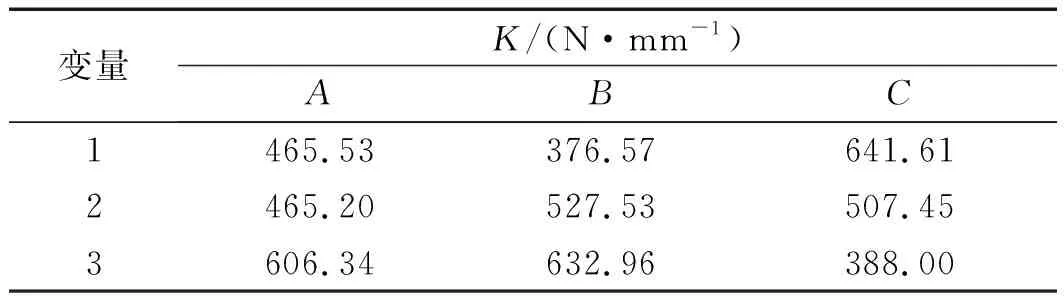
表4 各水平因子對剛度K的影響

3.2.3 因子對品質特性影響所占的比重

(5)

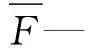
影響比重百分比是指各因子對F和K的影響比重與各因子對F和K的影響比重總和之比。

各變量對承載力及剛度的相對重要性如表5所示。

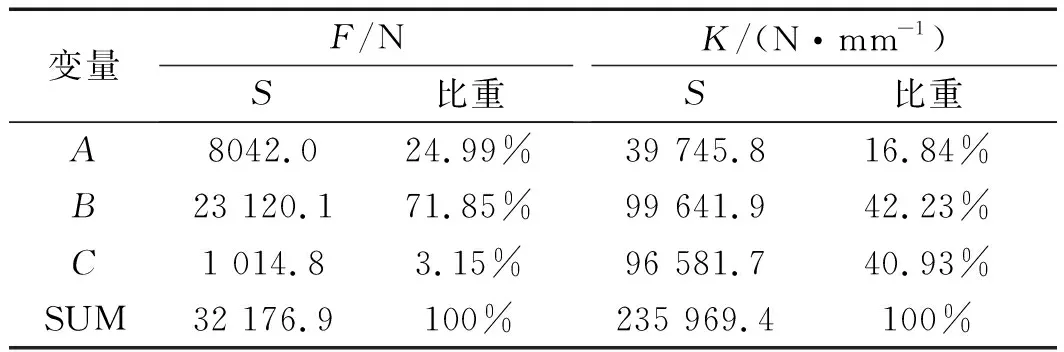
表5 各變量對承載力及剛度的相對重要性

由表5可知，高度g對F的影響比重最大，其次為磁環寬度w；磁環間氣隙g對K的影響最大。

3.2.4 結果分析

優化參數對性能指標的影響隨性能指標而變。筆者將表(3，4)中的數據用圖來表示，如圖6所示。

圖6 各因子水平對F及K的影響

由圖6可知，本次優化目標是使上軸向磁環的承載力、剛度在一定參數下能夠取到最大值。結合表(3，4)、圖6可知，當選擇承載力F為優化設計目標時，磁環的高度h所占比重最大；其次，磁環寬度w所占比重較大，因此，在選取參數時應優先考慮磁環高度和寬度的影響因子；當剛度K為上軸向磁環優化設計目標時，高度h所占比重最大，氣隙g次之。

綜合考慮各參數對上軸向磁環各性能指標影響的變化趨勢，筆者選擇優化后參數選取值如下：w=10 mm，h=5 mm，g=0.5 mm。

3.2.5 實驗及結果分析

為了進一步驗證優化結果的正確性，本文對優化前、后的上軸向磁環結構參數建立有限元仿真模型；以垂直向下的方向為正方向，對磁路矢量、軸向承載力、剛度進行仿真。

優化前、后磁路矢量對比如圖7所示。

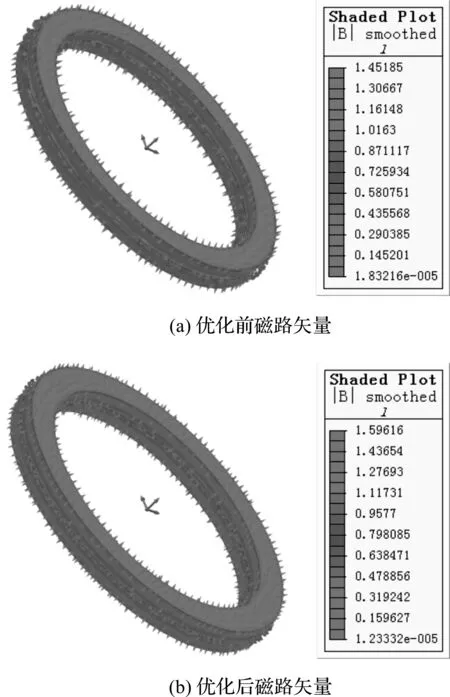
圖7 優化前、后磁路矢量對比

由圖7可知，優化后的上軸向磁環磁密由1.452 T提高到1.596 T。

優化前、后懸浮特性對比如圖8所示。

圖8 優化前、后懸浮特性對比

由圖8可知，靜止懸浮時，承載力由255.74 N增加到375.57 N，且優化后的承載力最小為333.95 N，大于重力200 N；優化后的剛度提高了1.5倍，且通過分析可知，剛度在各自象限內均為正值，表明該優化后的軸向磁環能夠克服重力，從而實現懸浮。

3.3 下軸向磁環結構設計

由前文可知，上軸向磁環提供的承載力為375 N，重力為200 N，故下軸向磁環應提供175 N的力，滿足系統力的平衡。

根據永磁體材料的抗磁曲線及退磁曲線，結合式(14)，可以計算出下軸向磁環參數為：寬度(w)×高度(h)×氣隙(g)=10 mm×2.81 mm×0.5 mm。

以豎直向上為正方向，對下軸向磁環進行仿真，下軸向磁環承載力及剛度由圖9所示。

圖9 下軸向磁環承載力及剛度

由圖9可知，下軸向磁環提供的承載力為175.19 N，誤差為0.1%；剛度均為正值，滿足懸浮設計要求。

3.4 軸向磁浮軸承徑向擾動

軸向磁浮軸承在軸向懸浮時，也會有來自徑向的擾動。筆者對軸向磁浮軸承在徑向以X軸正向為偏移正方向進行建模仿真。

軸向磁軸承徑向擾動下承載力如圖10所示。

圖10 軸向磁軸承徑向擾動下承載力

由圖10可知，在規定所能達到的最大徑向偏移中，上軸向磁環提供的承載力依舊維持在(375±4)N，遠大于200 N重力；軸向下軸向磁環提供的懸浮斥力維持在(175±3)N。以上表明，在徑向擾動下，該軸向磁軸承在垂直方向提供的承載力與重力之間的力矩平衡維持不變，軸向磁軸承系統可以穩定懸浮。

4 結束語

本文提出了一種適用于小型垂直軸風力發電機的磁浮軸承系統，對徑向磁浮軸承與軸向磁浮軸承進行了設計；利用Taguchi的優化方法，得到了軸向磁浮軸承磁環寬度、高度及氣隙的最佳組合，實現了最優化設計；利用仿真建模，驗證了該方法的有效性。得出了如下結論：

(1)由于在相同垂直高度下，徑向雙環磁浮軸承提供的剛度過小，筆者采用徑向疊加三環磁浮軸承，可增大磁密利用率，徑向剛度提高到原來的2.4倍，實現了轉子徑向懸浮；

(2)上軸向磁環經過多變量優化，軸向承載力提高了175 N，剛度提高了1.5倍；其與下軸向磁環構成了軸向磁浮軸承系統，平衡重力，實現了轉子軸向懸浮；

(3)在面對徑向擾動造成的徑向偏移時，軸向磁軸承的承載力沒有較大變化，上軸向磁環提供的承載力依舊維持在(375±4)N，軸向下軸向磁環提供的懸浮斥力維持在(175±3)N，表明該軸承能夠承受住徑向擾動實現穩定懸浮。