基于分位數(shù)回歸的針闊混交林樹(shù)高與胸徑的關(guān)系

張冬燕，王冬至，李 曉，高雨珊，李天宇，陳 靜

（1.河北農(nóng)業(yè)大學(xué) 林學(xué)院，河北 保定 071000；2.河北農(nóng)業(yè)大學(xué) 經(jīng)濟(jì)管理學(xué)院，河北 保定 071000）

樹(shù)高和胸徑不僅是用來(lái)預(yù)測(cè)林分蓄積量[1]、生物量[2]、立地生產(chǎn)力[2-3]及林分結(jié)構(gòu)[4]的重要變量，而且是森林資源調(diào)查及經(jīng)營(yíng)效果評(píng)價(jià)的重要因子。在標(biāo)準(zhǔn)地調(diào)查過(guò)程中，樹(shù)高測(cè)量難度較大且觀測(cè)成本高，其觀測(cè)誤差也相對(duì)較大，給精準(zhǔn)林業(yè)質(zhì)量提升帶來(lái)了一定困難[2,4]，而胸徑觀測(cè)方便且精度較高。因此，根據(jù)標(biāo)準(zhǔn)地調(diào)查數(shù)據(jù)，建立樹(shù)高與胸徑關(guān)系預(yù)測(cè)模型，可降低調(diào)查成本，提高預(yù)測(cè)精度[5]，這對(duì)于森林質(zhì)量精準(zhǔn)提升具有重要意義。當(dāng)前林業(yè)研究多采用線性或非線性樹(shù)高與胸徑關(guān)系模型來(lái)模擬預(yù)測(cè)兩者之間的關(guān)系，其參數(shù)估計(jì)方法多采用最小二乘法來(lái)模擬，然而最小二乘法是基于均值回歸，利用變量均值來(lái)擬合模型參數(shù)[6]，該方法要求調(diào)查數(shù)據(jù)需滿(mǎn)足獨(dú)立正態(tài)同分布等條件。在林業(yè)調(diào)查中，樹(shù)高與胸徑觀測(cè)數(shù)據(jù)不能滿(mǎn)足該要求，而分位數(shù)回歸對(duì)調(diào)查數(shù)據(jù)沒(méi)有嚴(yán)格要求[7]，利用變量條件分位數(shù)來(lái)建模[6]，對(duì)具有尖峰、厚尾、異方差顯著的數(shù)據(jù)擬合效果更加穩(wěn)健[8-10]。分位數(shù)回歸理論框架是由KOENKER[11]提出，已在醫(yī)學(xué)[12]、經(jīng)濟(jì)學(xué)[13]、教育與政策[14-15]及自然資源管理等領(lǐng)域進(jìn)行了研究與應(yīng)用。在林業(yè)相關(guān)研究中，分位數(shù)回歸被應(yīng)用于模擬林分自疏邊界線[16]、直徑分布規(guī)律[17]、林分密度指數(shù)[18]及森林病蟲(chóng)害[19]等方面研究。?Z?ELIK等[20]基于分位數(shù)回歸建立了樹(shù)高與胸徑關(guān)系模型，高慧淋等[21]采用此方法建立了長(zhǎng)白落葉松Larix olgensis人工林最大林分密度線模型，提高了模型預(yù)測(cè)精度及適用性。然而在華北暖溫帶針闊混交林中，如何基于一個(gè)分位數(shù)回歸模型，預(yù)測(cè)不同樹(shù)種樹(shù)高與胸徑關(guān)系是亟待解決的科學(xué)問(wèn)題。在混交林中為了描述樹(shù)種結(jié)構(gòu)對(duì)樹(shù)木生長(zhǎng)影響，部分學(xué)者[22-25]采用啞變量方法構(gòu)建了不同間伐方式、不同地域樹(shù)高曲線及生長(zhǎng)量預(yù)測(cè)模型。然而基于包含啞變量的非線性分位數(shù)回歸方法來(lái)構(gòu)建不同樹(shù)種樹(shù)高與胸徑關(guān)系模型的研究較少。因此，本研究以河北省塞罕壩華北落葉松Larix principisrupprechtii與白樺Betula platyphylla針闊混交林為研究對(duì)象，基于啞變量方法和分位數(shù)回歸相結(jié)合方法，構(gòu)建混交林不同樹(shù)種分位數(shù)回歸模型，為精確描述樹(shù)高與胸徑的關(guān)系提供依據(jù)。

1 研究區(qū)概況

河北省塞罕壩機(jī)械林場(chǎng)(41°22′～42°58′N(xiāo)，116°53′～118°31′E)位于河北省最北部，地勢(shì)北高南低，屬華北暖溫帶立地類(lèi)型區(qū)，林場(chǎng)總面積約9.2×104hm2，總蓄積約8.1×106m3。土壤類(lèi)型以褐色森林土、棕色森林土及風(fēng)沙土等為主；成土母質(zhì)主要為坡積物、殘積物及洪積物等；極端最高氣溫為33.4 ℃，最低氣溫-43.3 ℃，年均氣溫-1.3 ℃，年均無(wú)霜期64 d，年均降水量460.3 mm，是典型的半干旱半濕潤(rùn)寒溫性大陸季風(fēng)氣候。研究區(qū)植被類(lèi)型豐富，主要喬木樹(shù)種有華北落葉松、白樺、樟子松Pinus sylvestris、云杉Picea asperata等，主要灌木樹(shù)種有山刺玫Rosa daverica、胡枝子Lespedeza bicolor、沙棘Hippophae rhamnoides等，主要草本植物有地榆Sanguisorba offcinalis、唐松草Thalictrum aquilegifolium、曼陀羅Datura stramonium等。

2 研究方法

2.1 數(shù)據(jù)來(lái)源

在北曼店、大喚起、陰河、千層板和第三鄉(xiāng)等5個(gè)林場(chǎng)設(shè)立了83塊標(biāo)準(zhǔn)地(30 m×30 m)，對(duì)標(biāo)準(zhǔn)地內(nèi)各林分因子(林分密度、平均高、平均胸徑、樹(shù)種斷面積、林分總斷面積、優(yōu)勢(shì)高等)和立地因子(海拔、坡度、坡向、坡位、土層厚度等)進(jìn)行調(diào)查，共調(diào)查立木10 104株(華北落葉松5 258株，白樺4 846株)，林分年齡分布為24～45 a，不同標(biāo)準(zhǔn)地混交度分布為0.39～0.62。研究過(guò)程中，分樹(shù)種將觀測(cè)數(shù)據(jù)分別按3∶1分為建模數(shù)據(jù)(62塊標(biāo)準(zhǔn)地)和檢驗(yàn)數(shù)據(jù)(21塊標(biāo)準(zhǔn)地)，基本信息如表1和表2所示。

表1 模型建立數(shù)據(jù)Table 1 Data of establishment model

表2 模型檢驗(yàn)數(shù)據(jù)Table 2 Data of test model

2.2 基礎(chǔ)模型

在描述樹(shù)木生長(zhǎng)及樹(shù)高與胸徑關(guān)系的近百種不同模型中，Richard方程不但具有可解釋的生物學(xué)意義，而且具有易收斂且靈活性高等特性。部分研究基于Richard方程構(gòu)建了不同林分類(lèi)型樹(shù)高與胸徑關(guān)系的預(yù)測(cè)模型，均取得了較好的預(yù)測(cè)結(jié)果[18,20,26-29]。因此，本研究以Richard方程作為構(gòu)建華北落葉松與白樺針闊混交林樹(shù)高與胸徑關(guān)系基礎(chǔ)模型，模型表達(dá)如式(1)所示。

式(1)中：Hij為第i個(gè)樣地第j株樹(shù)的樹(shù)高(m)；dij為第i個(gè)樣地第j株樹(shù)的胸徑(cm)；a、b、c為基礎(chǔ)模型的參數(shù)；εij為誤差項(xiàng)。

2.3 啞變量

為了解決模型預(yù)測(cè)精度的影響，可以在模型中加入啞變量[23,30-32]。包含啞變量的樹(shù)高與胸徑關(guān)系預(yù)測(cè)模型，不僅可以實(shí)現(xiàn)模型對(duì)不同樹(shù)種相容性，而且在一定程度上可以提供模型預(yù)測(cè)精度及適用性，包含啞變量的樹(shù)高與胸徑關(guān)系預(yù)測(cè)模型表達(dá)如式(2)所示。

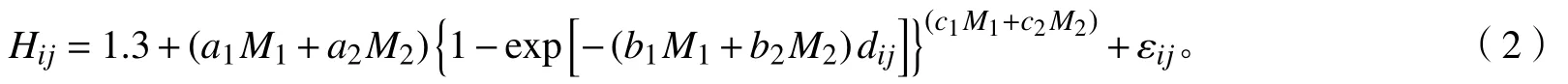
式(2)中：Mi為啞變量，當(dāng)M1=1、M2=0時(shí)為華北落葉松，當(dāng)M1=0、M2=1時(shí)為白樺；ai、bi、ci為模型參數(shù)；εij為誤差項(xiàng)。

2.4 分位數(shù)回歸

由于分位數(shù)回歸對(duì)模型誤差不需要嚴(yán)格假設(shè)條件，因此本研究基于Richard方程，選取5個(gè)分位點(diǎn)(τ=0.1、0.3、0.5、0.7、0.9)構(gòu)建不同樹(shù)種的樹(shù)高與胸徑關(guān)系預(yù)測(cè)模型，利用加權(quán)最小一乘法可以得到不同分位點(diǎn)參數(shù)估計(jì)值，具體見(jiàn)式(3)。

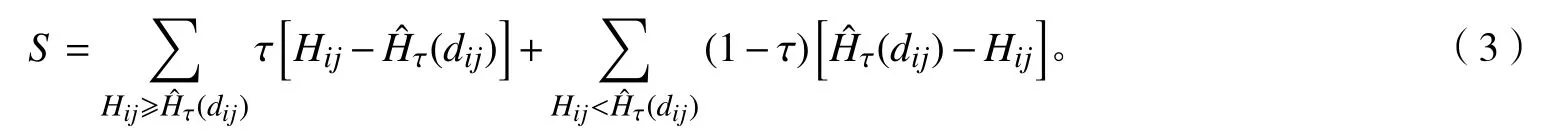
式(3)中：S為不同分位點(diǎn)估計(jì)值；τ、Hij分別為第i個(gè)樣地第j株樹(shù)在不同分位點(diǎn)τ樹(shù)高預(yù)測(cè)值與樹(shù)高值(m)；dij第i個(gè)樣地第j株樹(shù)胸徑(cm)；τ為分位點(diǎn)。

2.5 模型檢驗(yàn)與評(píng)價(jià)

統(tǒng)計(jì)分析均基于SPSS 24.0和SAS 9.4中的PROC NLIN和PROC NLP完成，基于模型確定系數(shù)(R2)、平均差(MD)、平均絕對(duì)誤差(MAD)對(duì)模型擬合精度及適用性進(jìn)行評(píng)價(jià)與比較。

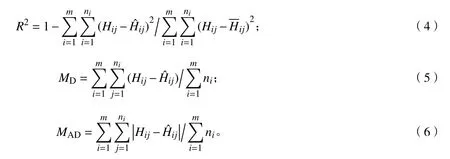
式(4)～(6)中：Hij、和分別為樹(shù)高觀測(cè)值、預(yù)測(cè)值和平均值；m為標(biāo)準(zhǔn)地?cái)?shù)量；n為標(biāo)準(zhǔn)地株數(shù)。

3 結(jié)果與分析

3.1 林分特征分析

圖1為不同樹(shù)種胸徑與樹(shù)高的關(guān)系。華北落葉松和白樺的樹(shù)高分別為4～18和6～16 m，胸徑分別為6～32和6～28 cm。

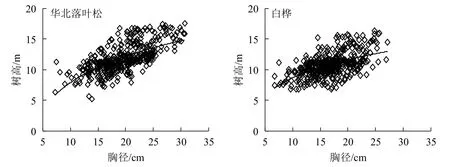
圖1 不同樹(shù)種胸徑與樹(shù)高分布Figure 1 Height-diameter distribution of different tree species

3.2 基礎(chǔ)模型和分位數(shù)模型擬合與評(píng)價(jià)

從表3可見(jiàn)：在華北落葉松與白樺針闊混交林中，基于分位數(shù)回歸的不同樹(shù)種不同分位點(diǎn)確定系數(shù)均大于傳統(tǒng)回歸方法，平均差及平均絕對(duì)誤差均小于傳統(tǒng)回歸方法。在確定的5個(gè)分位點(diǎn)中，當(dāng)分位點(diǎn)τ=0.7時(shí)，華北落葉松與白樺的樹(shù)高與胸徑關(guān)系預(yù)測(cè)模型精度最高。基于不同分位點(diǎn)預(yù)測(cè)模型建立了不同樹(shù)種在各分位點(diǎn)殘差分布圖(圖2)，確定當(dāng)分位點(diǎn)位為τ=0.7時(shí)，華北落葉松與白樺樹(shù)高與胸徑關(guān)系模型能夠更好描述兩者之間的關(guān)系。

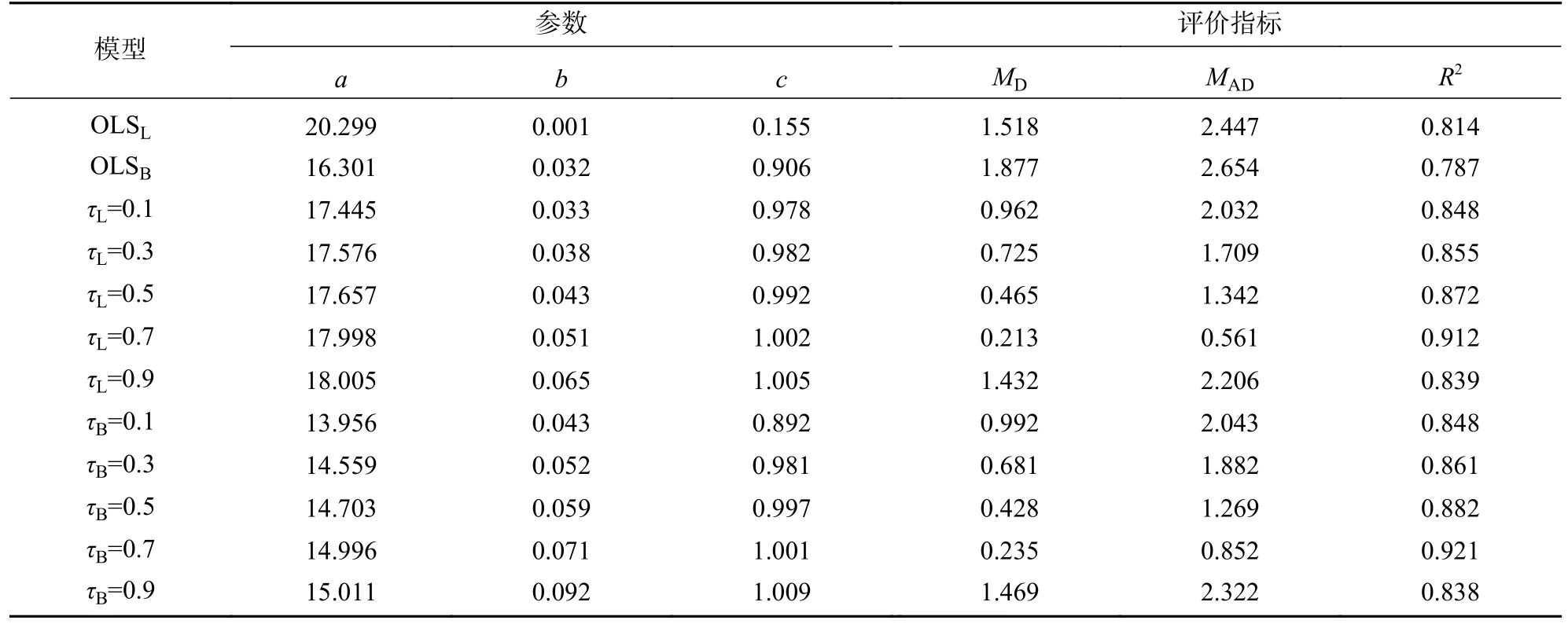
表3 基礎(chǔ)模型和分位數(shù)回歸模型擬合與評(píng)價(jià)Table 3 Fitting and evaluation of basic model and quantile regression model

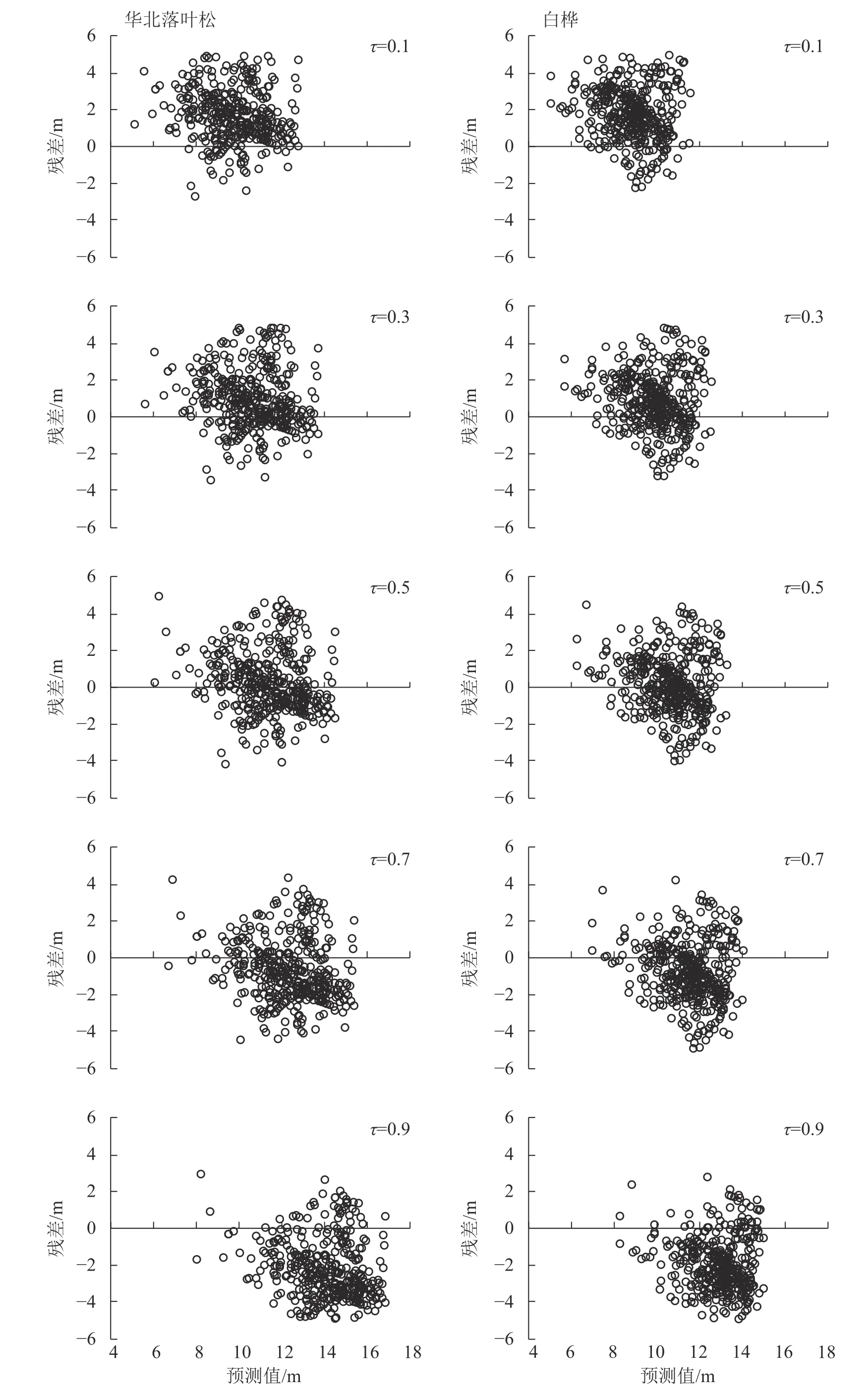
圖2 不同樹(shù)種各分位點(diǎn)殘差分布Figure 2 Residual distribution of each quantile of different tree species

3.3 不同樹(shù)種樹(shù)高模擬

基于不同分位點(diǎn)預(yù)測(cè)模型，分別對(duì)華北落葉松和白樺的樹(shù)高與胸徑關(guān)系進(jìn)行了模擬(圖3)。不同樹(shù)種在不同分位點(diǎn)樹(shù)高與胸徑關(guān)系預(yù)測(cè)趨勢(shì)及范圍基本一致，表明包含啞變量的分位數(shù)回歸模型預(yù)測(cè)效果較好。

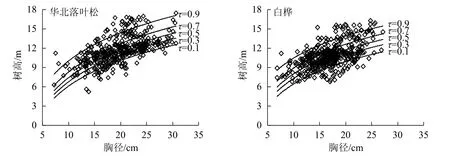
圖3 不同分位點(diǎn)樹(shù)高與胸徑的關(guān)系Figure 3 Relationship between tree height and DBH of different quantiles

4 討論

在描述樹(shù)高與胸徑關(guān)系的多種線性和非線性預(yù)測(cè)模型中，通常采用具有生物學(xué)意義且靈活性較高的Richard方程來(lái)研究不同林分類(lèi)型樹(shù)高與胸徑的關(guān)系[26,33]，因此，本研究將Richard方程作為構(gòu)建華北落葉松與白樺混交林樹(shù)高與胸徑關(guān)系基礎(chǔ)模型。對(duì)紅松Pinus koraiensis人工林、土耳其松Pinus brutia和黎巴嫩雪松Cedrus libani混交林的研究[20,26-28]表明：Richard方程是描述其樹(shù)高與胸徑關(guān)系的最優(yōu)模型。

在構(gòu)建樹(shù)木生長(zhǎng)及生物量預(yù)測(cè)模型中，包含啞變量模型具有更高的預(yù)測(cè)精度[22,25,31-32]。本研究在華北落葉松與白樺針闊混交林中，基于非線性分位數(shù)回歸構(gòu)建的包含啞變量樹(shù)高與胸徑的關(guān)系模型，其精度高于傳統(tǒng)回歸預(yù)測(cè)模型，這與人工林最大密度線確定[21]及樹(shù)高與胸徑關(guān)系模型[20]的研究結(jié)論相一致，表明非線性分位數(shù)回歸較傳統(tǒng)回歸方法更加穩(wěn)定，可用于人工林和混交林立地潛在生產(chǎn)力的評(píng)價(jià)。

5 結(jié)論

本研究以塞罕壩華北落葉松與白樺針闊混交林調(diào)查數(shù)據(jù)為基礎(chǔ)，確定Richard模型為描述不同樹(shù)種樹(shù)高與胸徑關(guān)系的基礎(chǔ)模型，在基礎(chǔ)模型中構(gòu)造一個(gè)表示樹(shù)種的啞變量，并利用分位數(shù)回歸在一個(gè)模型中同時(shí)估計(jì)不同樹(shù)種及不同分位點(diǎn)的樹(shù)高與胸徑關(guān)系模型參數(shù)，經(jīng)過(guò)檢驗(yàn)不同樹(shù)種分位數(shù)回歸模型均能較好反映樹(shù)高與胸徑的關(guān)系，當(dāng)分位點(diǎn)τ=0.7時(shí)，分位數(shù)回歸模型預(yù)測(cè)精度最高，擬合效果最好。