基于兩階段算法的帶時間窗車輛路徑研究
宿 愷, 趙 潔, 郭明順
(沈陽工業大學 管理學院, 沈陽 110870)
物流作為電商的重要要素之一,在時間上制約了電商行業的發展。如何優化車輛路徑、提高運輸效率,是電商行業在物流環節急需解決的問題[1]。現階段,許多車輛路徑規劃缺乏高效的線路設計,也未將時間延遲等情況考慮在內。能夠針對顧客的要求進行特定時間段的配送,對于降低企業運輸成本、改進客戶服務質量具有重要意義。對企業而言,如何進行合理的路徑規劃是降低生產成本的合理方式之一[2]。
在實際配送過程中,顧客分布點不均勻,許多智能優化算法[3-7]被提出用來解決配送實際問題。遺傳算法因極強的魯棒性及收斂速度快,能夠避免出現局部最優解;聚類算法在前期對客戶點進行聚類則可以大大提高配送效率。因此,本文對遺傳算法和聚類分析進行改進[8],將二者結合起來建立數學模型,并運用算例分析驗證其合理性和可行性。
一、數學模型建立
由于在實際情況中需求點分布失衡,導致在制定車輛路徑方案時若僅根據以往工作人員經驗會出現浪費時間和車輛的情況,尤其是在客戶對于配送時間段要求比較高的時候,如何將貨物準時送達是降低運輸時間成本、提高顧客滿意度所面臨的重要挑戰[9]。
本文建立的帶軟時間窗的車輛路徑優化模型主要出于以下幾方面考慮[10-11]:一是在顧客的規定時間進行貨物配送可以提高配送環節的服務質量,提高顧客滿意度;二是合理安排配送可以降低配送成本、提高配送效率從而帶來更大的效益,在定量的時間內合理分配時間;三是使得車輛得到合理利用,用最大的負載率完成特定的任務,減少車輛空間冗余情況,同時緩解城市交通擁堵狀況。
據此本文的VRPTW問題可以描述為:在軟時間窗的條件下,針對不同客戶定制不同的配送方案,使得滿足車輛負載限制、交通情況等約束條件時總運輸成本最低。
1. 基本假設及符號定義
基本假設:
(1) 配送為單向,即在商品運輸過程中只進行配送,不提供其他服務。
(2) 每次配送要求從固定配送中心出發,開始和結束位置相同,所有車輛在完成若干客戶的服務后必須返回相應的配送中心。
(3) 所有車輛的載重不超過負載能力。
(4) 所有車輛車種相同,且容量可知。
(5) 每個客戶僅被服務一次。
(6) 每個客戶都有一個指定服務時間[Ei,Li],客戶可接受在規定時間外服務,企業接受在規定時間外服務產生的懲罰成本。
(7) 客戶需求量已知,該點貨運只能由一輛車完成,且所有客戶都獲得該服務。
(8) 假定車輛配送成本即為車輛配送距離。
(9) 所有服務均不考慮服務時間。
(10) 假設路況均為順暢,對車輛行駛不造成影響。
上述參數的符號定義如表1所示。

表1 參數符號及含義
如果車輛在客戶要求時間Ei之前到達,則會產生等待成本;如果在Li之后到達,則需要支付一定罰金。懲罰函數Pi(Si)表示懲罰成本的高低,定義如下[12]:
(1)
式中,ai、bi表示懲罰系數。
2. 模型建立
本文模型目標是在配送過程中使運輸成本最低,根據以上假設建立模型:
(2)
(3)
(4)
(5)
(6)
(7)
(8)
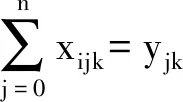
(9)
ti+Si+tij-M(1-xijk)≤tj
?i,j∈(1,2,…,n),k∈(1,2,…,K)
(10)
(11)
(12)
(13)
式(2)為配送成本最小的目標函數;式(3)表示編號為k的車輛最大載重量不超過車輛的負荷;式(4)表示從配送中心一共出發了K輛車進行服務;式(5)表示每個客戶只能由一輛車進行服務;式(6)表示車輛完成相應顧客服務后要返回配送中心;式(7)表示所有車輛配送的顧客之和等于有貨物需求的客戶總數;式(8)、(9)表示0~1決策變量x、y之間的關系;式(10)保證了車輛行駛路線的總耗時不超過預先設定范圍,以滿足客戶對供貨時間的要求;式(11)表示出發時間和返回時間均在設定時間范圍內;式(12)表示VRPTW有向圖的權重值,當編號為k的車輛途徑客戶i完成對客戶j的服務時xijk=1,否則xijk=0;式(13)表示當客戶i的服務由編號為k的車輛負責時變量yijk=1,否則yijk=0。
上述模型充分考慮了實際約束情況,接近實際問題,得到的解為全局解,對于解決具體問題有很好的借鑒作用。
二、相關算法概述
1. K均值算法概述
K均值算法是一種迭代求解的聚類分析算法,其優點是可以使數據形成類,從而快速對繁瑣復雜的事物進行分類,使得相似度高的事物聚集到一起分為一類。本文使用的K均值算法是非系統聚類方法中常用的一種。
2. 遺傳算法概述
遺傳算法是啟發式算法之一,與傳統算法相比迭代速度更快,能避免時間上的浪費。遺傳算法模擬自然環境中的物種進化過程來選擇優良個體和保留部分變異,可以用于復雜問題的優化計算,具有實際應用價值[13-14]。在產生初始種群之后,根據優勝劣汰的原則使后代適應度越來越高。在每一代中,根據個體適應度的不同選擇一些較為優良的個體,并在進化過程中參與交叉、變異,同時設定相應的交叉算子及變異算子來幫助產生下一代。待優化過程結束之后,可以產生新種群的最佳個體,這時得到的解作為實際問題的近似最優解。
三、算法實現操作
1. 聚類分析設計
聚類數目根據具體數據的車輛數確定。聚類完成以后,為了保證每個類中的需求總量不會超過每輛車的負載量,在每加入下一個客戶時要檢查貨物總重量是否超過車輛負荷,若超過則將不滿足條件的客戶從此群中去除。此時被犧牲的客戶為距離聚類中心最遠的那個客戶,對該客戶繼續采用聚類算法將其加入其他類中,直到沒有客戶被犧牲為止。具體步驟為[15-16]:
步驟1 在系統中導入原始數據文件,包含客戶坐標、時間要求、車輛負荷等。
步驟2 計算需要的車輛數目,對客戶進行分群,直到所有客戶點都被分配。
步驟3 檢查各群內的顧客總需求量是否超出車輛最大載重量。若超過則執行步驟4,否則執行步驟8。
步驟4 去除距離聚類中心最遠且超過車輛負荷的客戶,直到符合車輛負荷要求。
步驟5 檢查其他客戶群的車輛是否有剩余容量。如果有則執行步驟6,否則執行步驟7。
步驟6 將剔除的客戶加入到距離最近且加入后不超過車輛最大容量的客戶群,并執行步驟8。
步驟7 分配一輛車服務,回到步驟2。
步驟8 聚類完成,得到的編碼即為遺傳算法的配送中心點。
2. 遺傳算法設計
(1) 編碼設計。遺傳算法通常使用二進制編碼,但這種編碼方式可能會在計算過程中出現無效解。因此本文采用自然數編碼形式,這種編碼方式對于路徑優化來說能在很大程度上提高運算效率[17]。
當被服務客戶數量為n,服務車輛數量為m時,整個染色體的長度為m+n+1,所有染色體表示為{0,…,S1,S2,0,S3,…,Sn,0},其中Si表示第i個客戶點,出現0的個數與配送貨物所需車輛的數量有關。用0代表配送中心對各個路段進行劃分,便于觀察車輛的具體路徑。
(2) 適應度函數設計。在遺傳算法中,適應度函數值大小與染色體能否遺傳到下一代具有重要關聯[18]。本文所建立的模型以運輸費用最低為目標,因此適應度函數為運輸費用的倒數,運輸費用越小,適應度函數值越大,可行性越高,其關系表達式為
ai=1/bi(i=1,2,…,g)
(14)
式中:ai表示個體適應度;bi表示第i個個體對應的運輸費用;g表示種群規模。
(3) 選擇設計。采用最佳個體保留策略和比例選擇策略相結合的方法對選擇算子進行設計[19]。選擇方式如下:①根據適應度函數計算每個個體的適應度,然后根據數值降序排列,將排序后的個體平均分成3份[20]。②將處于排序前1/3的個體倍數增加。③處于中間1/3的個體直接復制。④處于排序后1/3的個體直接淘汰。當種群進化到后期階段,直接采用最佳個體保留法,不再參加其余進化過程,提高種群優良性。
(4) 交叉。交叉操作的作用是在進化過程中通過染色體片段的交換來形成新的個體,降低對優良模式的破壞概率。本文采用順序交叉法,確保前一代的優良個體能夠順利得到遺傳,同時增加了個體多樣性。例如:
A(136458792)→A′(1364|5879|2)→
A1(243158796)
B(279431865)→B′(2794|3186|5)→
B1(457931862)
(5) 變異。在遺傳過程中會出現一定概率的基因突變。變異算子用來表示這種現象可能發生的概率,改變染色體中的基因片段,呈現出基因多樣性[21]。本文采用逆轉變異對染色體中的基因片段進行調整。該方法能夠對種群中的變異進行適當調整,在一定程度上防止過早收斂的現象。例如:
A(136458792)→A′(13|645|8792)→
A1(135468792)
(6) 終止規則。作為一種隨機搜索算法,遺傳算法需要提前設定終止條件來保證在一定時間內結束迭代循環。本文設定為進化次數達到100則停止運算[22]。
四、仿真實驗與性能分析
采用MATLAB2018a軟件實現該算法對帶時間窗的車輛路徑優化問題的求解過程。為進一步驗證兩階段算法的性能,與經典遺傳算法的算法性能進行對比分析,使用Solomon數據集進行仿真測試。選取數據集r106,如表2所示。
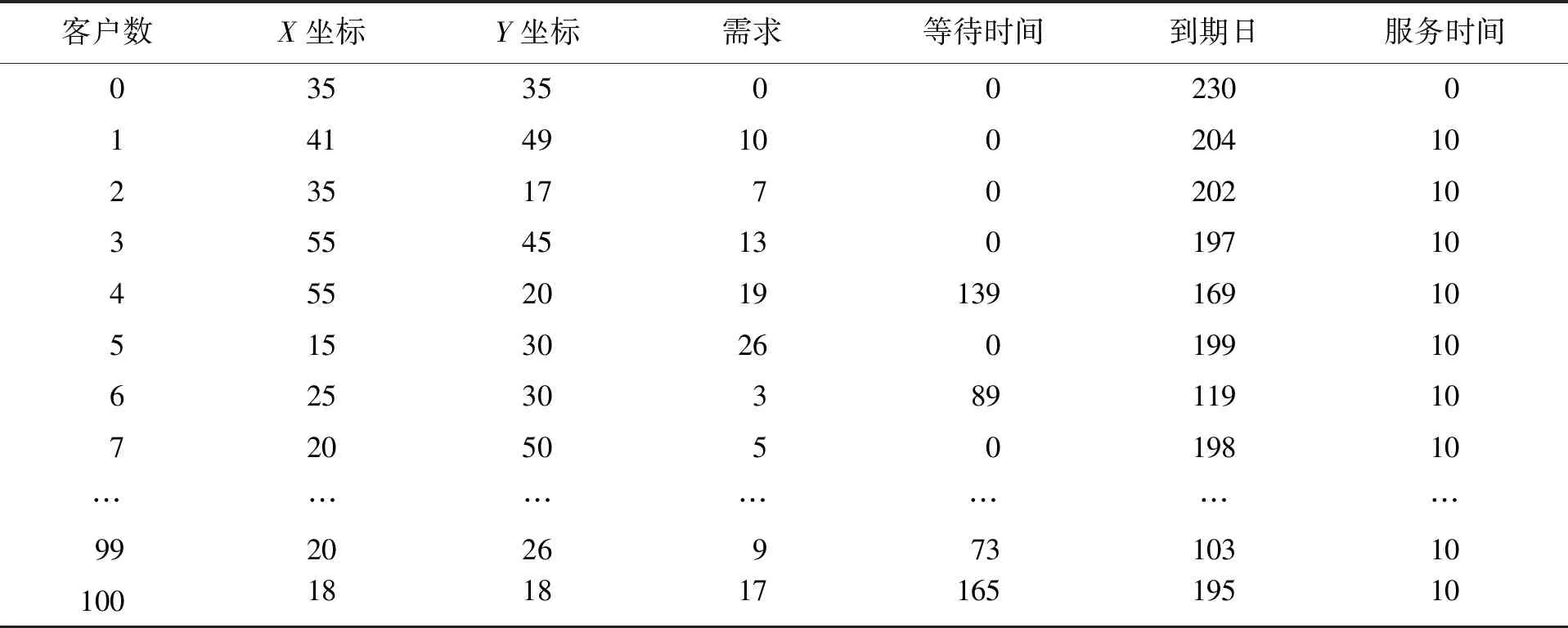
表2 客戶需求點
仿真過程中相關運算參數設定如表3所示。

表3 實驗參數設置
實驗結果及相關對比如圖1~3所示。圖1表示實驗數據在第一階段聚類分析之后得到的初始聚類中心以及各分布點位置。
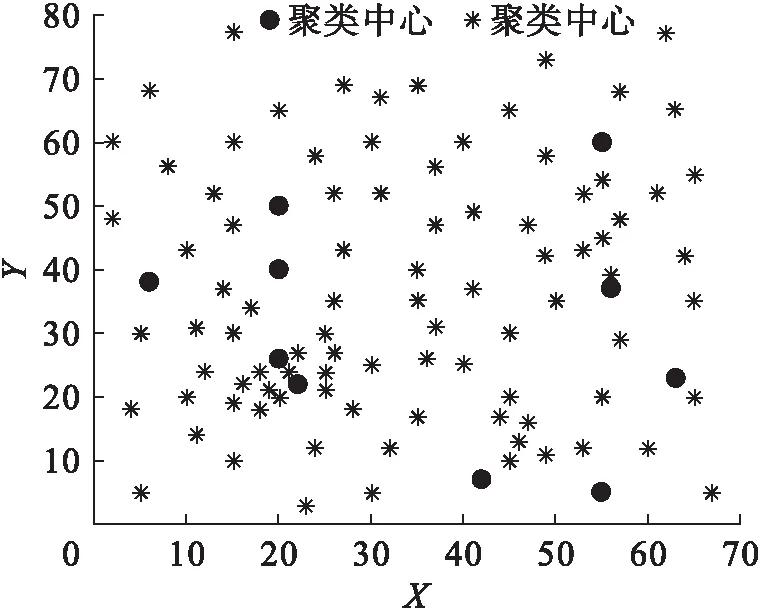
圖1 客戶位置分布
圖2表示運用經典遺傳算法運算得到的仿真路徑。圖3表示加入聚類分析并對遺傳算法進行改進之后得到的仿真路徑,從中可以看出改進的算法能夠明顯對需求點進行分類配送。
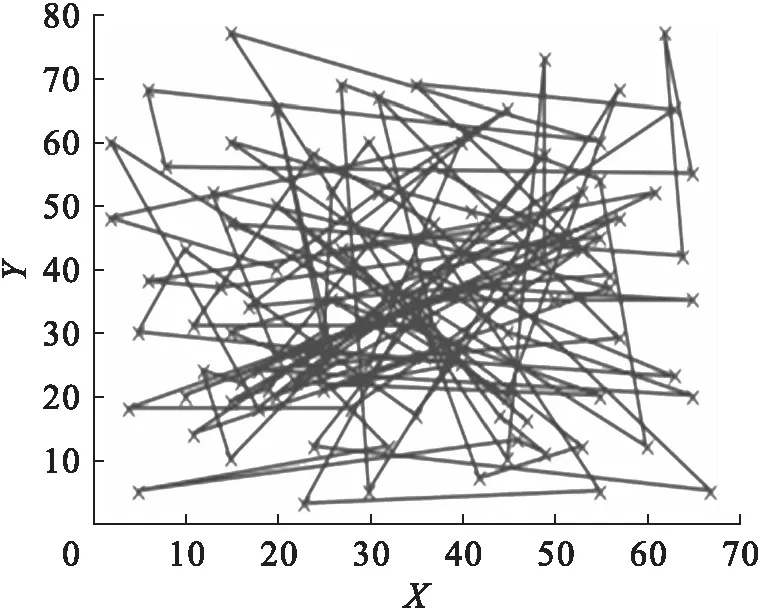
圖2 經典遺傳算法配送路線
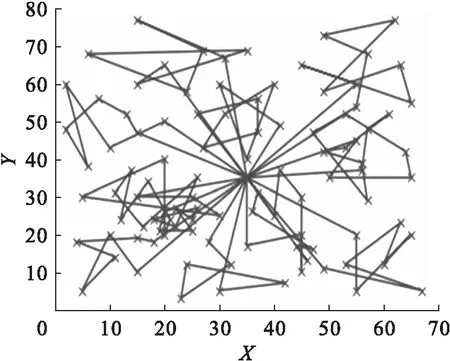
圖3 改進遺傳算法配送路線
為驗證兩階段算法在求解問題時的最優性,對兩階段算法求解結果與經典遺傳算法進行對比,如表4、5所示。

表4 兩階段算法求得的最優解

表4(續)
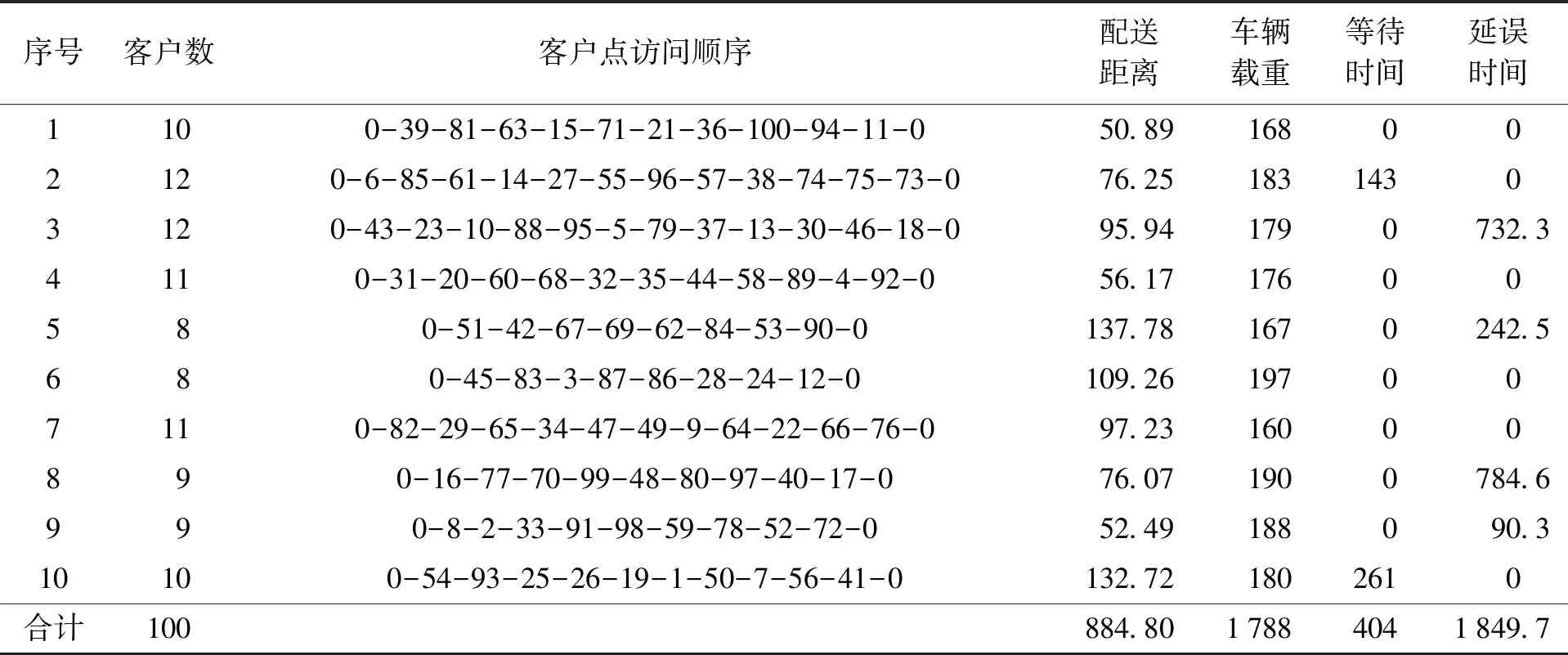
表5 經典遺傳算法求得的最優解
對比表4、5可以看出,本文采用兩階段算法求得的最優解相對于經典遺傳算法在等待時間和延誤時間上有明顯優勢,更符合帶時間窗的車輛路徑優化問題對時間窗的要求,提高了服務效率。
從Solomon數據集中另外選出4組數據進行仿真,得出實驗數據如表6、7所示。對比可見改進算法可以明顯優化計算結果。

表6 實驗最優運行時間對比

表7 實驗最優運輸成本對比
五、結 語
為更好地解決物流配送中存在的顧客時間限制問題,本文提出將聚類分析和遺傳算法相結合的兩階段算法并對其進行改進。使用Solomon數據集進行算例分析并進行對比,結果表明該算法在求解帶軟時間窗的車輛路徑優化問題時具有良好的可行性,能夠提供最優方案。

