石榴氈蚧種群的空間格局及其抽樣模型的建立

徐 睿，孫丹萍，王朝陽

（河南林業職業學院，河南 洛陽 471002）

在自然界中，任何昆蟲的種群都是以一定的空間格局進行分布的。種群空間格局是指昆蟲種群在空間上的分布方式[1]。空間格局是昆蟲種群的重要特性，也是昆蟲的生物學特性，代表著昆蟲生存空間需求的特征及動態變化，反映了昆蟲在生態環境中的生存方式，并受到了外界環境條件的影響[2-4]。了解昆蟲的種群空間格局對掌握種群的發展、擴散、猖獗、消亡的預測預報及制訂可持續害蟲控制策略等有重要的意義[2,5]。昆蟲的種群空間格局受到許多因素的影響，包括生態環境、昆蟲習性等。研究種群空間格局的生態學目的之一是了解環境對種群的影響，不僅要分析影響其分布的環境因素，還要研究環境對種群分布產生的影響[6]。

有關昆蟲種群空間格局抽樣模型的研究報道較多，抽樣模型必須符合4 個特點：準確、簡單、迅速、廉價[2]。目前，比較普遍采用的抽樣模型包括聚集度指標法、線性回歸法、擴散型指數法等[7-11]。常亞文等[7]研究了三葉斑潛蠅幼蟲在番茄和豇豆上的空間格局分布，同時對抽樣技術進行了研究。結果表明，三葉斑潛蠅幼蟲在2 個寄主上均呈聚集分布，且以個體群形式存在。同時，采用Kc 法、Iwao 法及Taylor 冪法計算出了在不同精度下三葉斑潛蠅田間的理論抽樣數。陳紅星等[12]通過對垂葉榕不同方位和高度的隨機取樣，運用5 種聚集度指標以及Taylor 冪法和Iwao 回歸模型分析和測定了榕管薊馬Gyuaikothrips uzedli的種群空間格局，同時應用Iwao 理論抽樣模型確定了榕管薊馬不同種群密度與不同精度要求下的理論抽樣數。潘杰[2]采用地統計學方法分析了受害程度不同的油松純林和混交林林分內紅脂大小蠹種群的空間分布格局，發現輕度受害純林與重度受害純林林分內紅脂大小蠹種群均表現為較強的空間聚集性，而混交林受害林分內其種群表現為隨機分布。受害程度不同的純林林分內紅脂大小蠹種群空間格局具有一定的差異，而且純林與混交林林分內其種群空間格局也有較大的差別。近年來，隨著蟲害防控技術的升級以及抽樣技術的成熟，我國在森林保護領域的害蟲控制、預測預報模型等方面的研究均獲得了較好的成果。

石榴Punica granatumL.的市場價值高，種植前景好，在我國種植范圍廣。軟籽石榴新品種是目前我國大力發展的經濟樹種之一，種植面積不斷擴大，經濟效益大幅提升。但近年來，石榴氈蚧的危害呈現日益加重的趨勢。石榴氈蚧又名紫薇絨蚧、石榴粉蚧、石榴絨蚧，屬同翅目Homoptera 絨蚧科Eriococcidae 絨粉蚧屬Eriococcus，為害石榴、蘋果、紫薇、大豆等多種花果樹木和農田作物，其若蟲和雌成蟲寄生于小枝、葉片主脈基部、芽腋、嫩梢或枝干等部位刺吸汁液，常造成樹勢衰弱，生長不良。蟲口密度大時，枝葉發黑，葉片早落，開花異常，嚴重影響樹木生長和果品的質量、產量及商品價值。2013年，石榴氈蚧被列入我國林業危險性有害生物名單[13-15]。昆蟲的空間分布狀況是其種群的重要生態學屬性[16]。通過研究石榴氈蚧種群的空間分布格局，了解其空間結構，從而確定田間不同允許誤差下的最大抽樣數量及序貫抽樣技術，使蟲情調查結果能夠更加客觀地反映種群的動態變化趨勢，及時掌握最有利防治時機，對石榴氈蚧的科學測報和高效防控具有重要的指導 意義[17-21]。

1 材料與方法

1.1 取樣方法

2016年7—8月，石榴氈蚧發生期，在鄭州市和靈寶市的果園、綠地等不同立地條件下，選擇8個樣地，每個樣地按照平行線法選取10 株樹，每株樹分別按東、西、南、北、中5 個方位，每方位選取4 片葉或20 cm 小枝1 根，檢查統計每個處理的蚧蟲數量。

1.2 空間分布型測定

1.2.1 聚集度指標法

根據調查數據，以樣地為單位，計算樣本數均值m（頭/葉）和樣本方差V，采用以下聚集度指標[2-9]進行檢驗分析。

1）Caasier 擴散系數（C值）

C=V/m。

當C=1 時，種群為隨機分布；當C＞1 時，為聚集分布；當C＜1 時，為均勻分布。

2）Waters 負二項分布參數（k值）

k=m2/(V-m)。

k值愈小，種群聚集度愈大；當k＞8 時則接近Poisson 分布。

3）Lloyd 聚塊性指標（m*/m）

m*=m+V/m- 1。

當m*/m=1 時，種群為隨機分布；當m*/m＞1時，為聚集分布；當m*/m＜1 時，為均勻分布。

4）Cassie & Kunou 指標（CA）

CA= (V-m)/m2。

當CA=0 時，種群為隨機分布；當CA＞0 時，為聚集分布；當CA＜0 時，為均勻分布。

5）David & Moore 叢生指標（IDM）

IDM=V/m- 1。

當IDM=0 時，種群為隨機分布；當IDM＞0 時，為聚集分布；當IDM＜0 時，為均勻分布。

6）蘭星平Lα指標

Lα=m-m/V+ 1。

當Lα/m=1 時，種群為隨機分布；當Lα/m＞1時，為聚集分布；當Lα/m＜1 時，為均勻分布。

7）張連翔Z/V指標

Z=V/m- 1+V。

當Z/V=1 時，種群為隨機分布；當Z/V＞1 時，為聚集分布；當Z/V＜1 時，為均勻分布。

1.2.2 線性回歸分析法

1）TaylorV-m冪法則（V=amb）回歸模型

lgV= lga+blgm。

式中：V為樣本方差，m為樣本平均值，a、b為引入的參數。當lga=0 且b=1 時，種群為隨機分布；當lga＞0 且b=1 時，種群為聚集分布；當lga＞0且b＞1時，種群為聚集分布；當lga＜0且b=1時，種群為均勻分布。

2）Iwaom*/m回歸模型

m*=a+bm。

式中：m為樣本均值，a、b為引入參數。當a=0且b=1 時，種群為隨機分布；當a＞0 且b=1 時，為聚集分布，分布的基本成分為隨機分布的個體群；當a=0 且b＞1 時為負二項分布；當a＞0且b＞1 時為聚集分布的個體群。當a=0 且b＜1或0 ＞a＞-1 且b=1 時為均勻分布。

3）蘭星平c′-m模型

c′=a+bm。

式中：a、b為待估參數，m為均值。當c′、m線性相關顯著時，a、b不同組合型揭示種群不同的空間分布型。

c′ = 1 /c+m。

式中：c為擴散系數。當a≤1 且b＜1 或a＜1且b≤1 時，為聚集分布；當a=1 且b=1 時，為隨機分布；當a≥1 且b＞1 或a＞1 且b≥1 時，為均勻分布。

1.3 聚集因素分析

運用Blackith 種群聚集均數（λ）檢驗石榴氈蚧種群的聚集原因。

式中：k為負二項分布的指數，γ是χ2分布表中自由度等于2k概率（P=0.5）對應的χ2值。在此基礎上進行λ-m線性回歸分析，確定聚集原因。當λ＜2時，種群聚集原因可能是某些環境因子的作用；當λ≥2 時，種群聚集原因是環境因子和昆蟲習性的綜合作用。

1.4 抽樣分析

1.4.1 理論抽樣分析

在確保調查質量的前提下，須抽取的最少樣本數為理論抽樣數。根據Iwaom*/m回歸模型提出的理論抽樣模型公式進行分析確定。

式中：t為置信度，實際調查中t取1；D為允許相對誤差；m為估計的蟲口密度；a、b為Iwaom*/m回歸模型參數。

1.4.2 序貫抽樣分析

用Iwaom*/m序貫抽樣決策模型公式，通過拒絕限和接受限（二者合稱“決策限”）來確定石榴氈蚧的序貫抽樣模型公式及最大理論抽樣數公式。

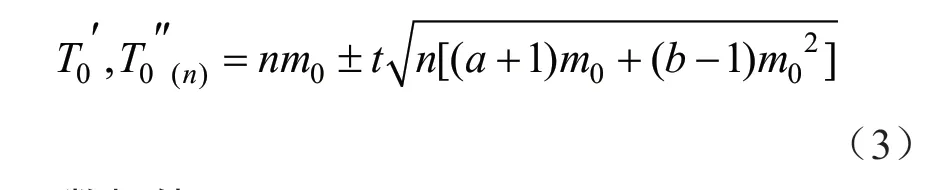
1.5 數據處理

調查數據采用DPS 軟件進行處理分析。

2 結果與分析

2.1 種群空間分布型

2.1.1 聚集度指標檢驗

應用7 種聚集度指標分別對調查數據進行檢驗分析，結果見表1。由表1 可知，擴散系數C和聚集指標m*/m值均大于1；負二項分布k值，2 個樣地k＜1，6 個樣地k＞1，且均小于8；Cassie 指標CA和叢生指標IDM值均大于0；Lα指標Lα/m和Z指標Z/V值均大于1。這些聚集度指標數值均符合聚集分布的檢驗標準，表明石榴氈蚧種群的空間分布型為聚集分布。

2.1.2 回歸模型檢驗

石榴氈蚧種群空間分布的回歸模型分析結果見表2。由表2 可知，根據Taylor 冪法則回歸模型檢驗結果，lga=0.696 2 ＞0，b=1.501 5 ＞1，種群為聚集分布，分布具有密度依賴性，說明石榴氈蚧種群在任意密度下都是聚集的，其聚集強度隨種群密度升高而增加。根據Iwaom*/m模型檢驗結果，a=14.886 0 ＞0，說明石榴氈蚧個體間相互吸引，分布的基本成分是個體群；b=1.382 6 ＞1，說明種群個體群為聚集分布，且符合負二項分布。根據蘭星平c′-m模型檢驗結果，a=0.058 4 ＜1，b=0.999 3 ＜1，說明石榴氈蚧種群為聚集分布。 3 種模型擬合優度均在0.8 以上，擬合效果較好，表明石榴氈蚧種群的空間分布型為聚集分布，這與采用聚集度指標法測定的結果相一致。

表1 石榴氈蚧種群的聚集度指標分析結果Table 1 Analysis result of aggregation degree indexes of E.lagerstroemiae population

表2 石榴氈蚧種群空間分布的回歸模型分析結果Table 2 Analysis result of spatial distribution regression models of E.lagerstroemiae population

2.1.3 聚集因素分析

通過式（1）計算Blackith 種群聚集均數（λ），結果見表3。由表3 可知，λ值均遠大于2，說明其聚集可能是由于某些環境因子作用所引起，也可能是昆蟲自身聚集習性作用的結果。

對各組樣本數均值（m）與聚集均數（λ）進行相關分析，得出回歸方程：λ=0.509 7m-0.342 8，R2=0.723 7（圖1）。由圖1 可以看出，石榴氈蚧聚集均數隨平均蟲口密度增加而不斷增大。若令λ=2，則m=4.596 4。即當每葉石榴氈蚧蟲口數量小于4.596 4 頭時，其聚集原因是由環境因子引起；當每葉蟲口數量大于或等于4.596 4 頭時，其聚集可能是由環境因子引起，也可能是由石榴氈蚧自身的聚集習性引起。本研究中，每葉石榴氈蚧蟲口數量均大于4.596 4 頭，表明石榴氈蚧聚集是自身的生活習性、行為及環境因子綜合影響的結果。經調查發現，自然情況下石榴氈蚧大多營固定生活，活動范圍小，自主擴散能力弱，分布具有局限性，個體間相互吸引，形成基本個體群。石榴氈蚧繁殖能力強，隨著繁殖量的增加，個體數量和蟲口密度不斷增加，個體群規模也隨之增大。此外，石榴氈蚧在果園、綠地等多呈團塊狀分布，在一定程度上限定了其擴散的空間范圍，從而呈現團塊狀密集分布的特點。這些因素與數據分析結果基本吻合，說明石榴氈蚧聚集是其自身的聚集習性與環境因子綜合影響的結果。

表3 石榴氈蚧種群聚集均數與樣本數均值分析結果 Table 3 Analysis result of average aggregation sizes and average sample number of E.lagerstroemiae population

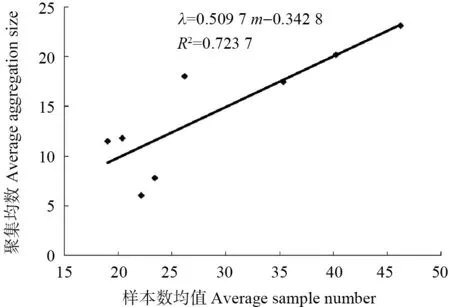
圖1 石榴氈蚧種群聚集均數（λ）與樣本數均值（m）的 關系Fig.1 Relation between average aggregation size (λ) and average sample number (m) of E.lagerstroemiae population

2.2 抽樣模型的建立

2.2.1 理論抽樣模型的建立

根據Iwao 理論抽樣公式，將已經建立的Iwaom*/m回歸模型中的參數a=14.886 0、b=1.382 6、t=1，代入式（2），可建立石榴氈蚧的最適理論抽樣模型n=(1/D)2(15.886 0/m+ 0.382 6)，確定不同蟲口密度、不同誤差條件下的最適理論抽樣數（表4）。

由于寄主植物數量常是有限的，即總體有限，故在實際抽樣中應校正公式：

n′=n/(1 +n/N)。

式中：N為總體數，n′為校正后的理論抽樣數。

2.2.2 序貫抽樣模型的建立

根據蚧蟲一般防治指標為5 頭/葉，將t=1、m0=5、a=14.886 0、b=1.382 6代入式（3），可得石榴氈蚧種群序貫抽樣決策模型公式：若取一系列n值（n=5，10，15，20，…），可得不同累計蟲口數相應抽樣數的上、下限值（T′0(n)、T″0(n)），結果見表5。

在實際應用中，若抽取樣本的累計蟲口數總是介于上、下限（T0′、T0″）之間，則實際抽取樣本數應不大于最大理論抽樣數nmax，即nmax=[(14.886 0+1)/m0+1.382 6-1]/D2。 令D=0.1，則nmax=356；D=0.2，則nmax=89，并以其最接近的界限方程得出結論。

表4 石榴氈蚧種群最適理論抽樣數Table 4 Optimum theoretical sampling number of E.lagerstroemiae population

3 結論與討論

本研究結果表明，石榴氈蚧種群空間分布型為聚集型負二項分布，且分布具有密度依賴性，石榴氈蚧種群在任意密度下都是聚集的，其聚集強度隨種群密度升高而增加。石榴氈蚧種群聚集分布是由其生活習性及環境因素共同影響的結果。總的來說，這是石榴氈蚧種群對生態環境適應的結果。

表5 石榴氈蚧種群序貫抽樣數Table 5 Sequential sampling number of E.lagerstroemiae population

在進行田間調查時，為了獲得準確的調查資料，可結合生產實際，應用最適理論抽樣數模型和最佳序貫抽樣模型進行序貫抽樣。當調查的累計蟲口數量達到預定蟲口數量指標時，應停止調查，累計蟲口數量除以取樣數，即平均蟲口密度。在生產實際中，據此可以精準監測蟲情，把握最有利防治時機，制定經濟、安全、高效的防控對策，控制石榴氈蚧的危害。

3.1 石榴氈蚧種群空間格局

分析種群空間格局是種群生態學的重要研究內容，可揭示種群在生境空間的擴展情況[22]。目前，有關蚧類種群空間格局的研究主要集中在扶桑綿粉蚧Phenacoccus solenopsis、松突圓 蚧Hemiberlesia pitysophila、矢尖蚧Unaspis yanoncnsis、楊盾蚧Diaspidiotus slavonicus等[22-25]。 有關石榴氈蚧種群空間格局的研究鮮見報道。昆蟲種群的空間格局是認識昆蟲的生態學特性的基礎之一。本研究中發現，石榴氈蚧種群空間分布為聚集型分布，這與黃俊等[22]得出的檢疫性有害生物扶桑綿粉蚧雌成蟲在大花馬齒莧上的空間格局是相似的，且兩者均具有密度依賴性。侯沁 文[23]應用聚集度指標和回歸分析，對松突圓蚧空間分布型進行研究，發現松突圓蚧的若蟲在松林中任意密度下均呈聚集分布，聚集度隨蟲口密度增大而增強，成蟲在松林中呈均勻分布。這與石榴氈蚧在任意密度下都是聚集的，且聚集強度隨種群密度升高而增加的結論相似。江西林等[24]研究了矢尖蚧在天竺桂葉片上的空間格局，發現其為聚集型分布，這與石榴氈蚧種群的空間格局是一 致的。

3.2 石榴氈蚧種群空間分布的影響因素

影響昆蟲種群空間分布的因素包括昆蟲的生活習性和外界環境。石榴氈蚧Blackith 種群聚集均數（λ）均遠大于2，由此可知種群聚集原因是環境因素和昆蟲習性共同作用的結果。一方面，石榴氈蚧生命力和繁殖力極強，尤其是在春末秋初，溫濕條件較適宜其發生和繁殖，繁殖速度快，短期內蟲口密度常會急劇增加；另一方面，石榴氈蚧種群相對固定的生活方式和雌成蟲固定產卵的習性是形成其聚集型分布格局的主要原因，具體原因有待進一步深入研究。對于松突圓蚧而言，若蟲聚集分布的原因主要與其集中產卵的方式有關。成蟲集中產卵后，其中大部分若蟲就近孵化，大量聚集孵化后由于食物競爭的原因，大量若蟲發育遲緩或死亡，成活率較低，小部分若蟲爬到遠處，因分散而營養充足，發育成成蟲，成活率較高，則成均勻分布[23]。天竺桂葉片上矢尖蚧的空間格局為聚集分布，可能與初孵若蚧的爬行行為和矢尖蚧天敵的聚集行為有關[24]。由此可知，對于這些昆蟲而言，影響種群空間分布的主導因素是其生活習性。此外，石榴等寄主植物的栽培方式及特點可能是其形成聚集型空間分布的重要因素之一，生態環境中氣候條件也直接影響著石榴氈蚧種群的分布狀況。由此說明，石榴氈蚧種群空間分布與寄主植物栽培配置方式、樹木生長狀況、氣候條件及蟲口密度等因素密切相關。

3.3 石榴氈蚧種群抽樣模型研究

確立最適抽樣數和抽樣模型是種群數量預測預報的基礎。目前，通常是通過預估抽樣模型的種群參數來確定蟲害的發生情況。賈蕊娟等[25]應用分布型指數研究了鳳凰木夜蛾Pericyma cruegeri幼蟲在鳳凰木Delonix regia上的空間分布型，利用Iwao 模型、Taylor 冪法則分析聚集原因，同時確定了幼蟲的最適理論抽樣數及序貫抽樣表，與本研究中所采用的抽樣模型類型一致，都能準確反映昆蟲的種群情況。此外，付園園等[26]在傳統抽樣分析方法的基礎上引入地統計學的方法，對不同林分類型的楊樹林內楊盾蚧的分布進行半變異函數擬合，建立高斯模型、指數模型、線性模型等。另外，傳統的方法存在一定的弊端，當混交林蟲情指數過低時，存在不能建立回歸方程、難以確認樣地之間空間分布的差異、無法描述蟲情峰值大小等問題，引入地統計學的方法后，通過制作昆蟲分布圖，可以形象地描述昆蟲分布情況，取得更好的效果。因此，為了更加清晰地描述石榴氈蚧在不同空間結構的格局，可以嘗試引入地統計學的方法來研究石榴氈蚧的防治[26-28]。