雙參數n階α次積分C半群的擾動定理

周裕然，趙華新，周 陽

(延安大學 數學與計算機科學學院，陜西 延安 716000)

算子半群的擾動理論是算子半群的重要內容之一，許多學者對此作了大量的研究工作[1-7]。文獻[8]中定理1給出了算子A+B生成雙參數半群{T(s,t)}s,t≥0的證明過程，其中設{T(s,t)}s,t≥0是Banach空間X上被算子A生成的雙參數C半群，B為有界線性算子。本文在此基礎上，改變定理1的條件，即將雙參數C半群換為雙參數n階α次積分C半群，得到新的擾動定理，并且推廣了相關結果。

1 預備知識

在本文中，X為無限維的復Banach空間，B(X)是X上有界線性算子全體所成的Banach代數；D(A)為線性算子A的定義域，設n∈N，α≥0。

T=0當且僅當存在n≥0，使JnT(s)=0，s≥0。

2 基本概念和引理

定義1[5]設n∈N，α≥0，C∈B(X)是單射，{T(s,t)}s,t≥0?B(X)強連續，若存在算子A=(A1,A2)使

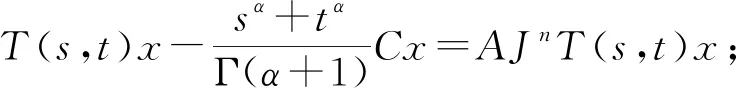
(2)CT(s,t)=T(0,t)T(s,0)；

(3)?x∈D(A),s,t≥0,

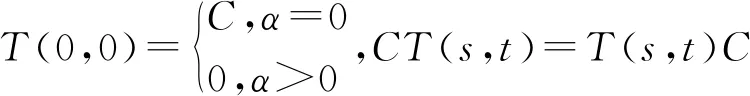
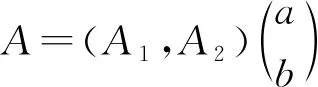
引理1[5](Hill-Yosida)設A=(A1,A2)為雙參數n階α次積分C半群{T(s,t)}s,t≥0的無窮小生成元，當且僅當：

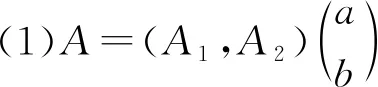
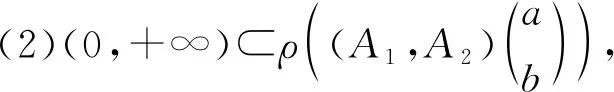
引理2[5]設{T(s,t)}s,t≥0是雙參數n階α次積分C半群，則存在M≥0,ω≥0使得

||T(s,t)||≤||C-1||M1eω1sM2eω2t≤

||C-1||Meω1s+ω2t，

3 主要結論

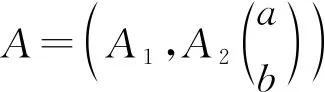
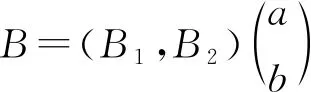
||S(s,0)||≤M1e(ω1+M1‖B1‖)s和

||S(0,t)||≤M1e(ω1+M1‖B1‖)t，

M1,M2≥1，ω1,ω2∈R。

因此，算子Ai+Bi(i=1，2)是閉稠定算子，

ρ(Ai+Bi)?(ω1+M1||B1||,+∞)并且λ>ωiMi||Bi||時，由拉普拉斯變換

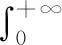
利用SAS 9.0軟件對試驗結果進行多因素方差分析（ANOVA）、最小二乘法（LSD）進行各水平之間的多重比較以及二次響應面回歸分析。

可知R(λ,Ai+Bi)(i=1,2)是有界線性算子，又因為

||CR(λ,(A1+B1,A2+B2))x||=

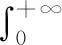
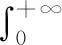
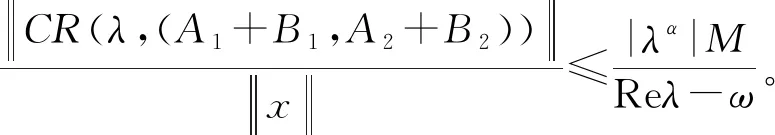
令S(s,t)=C-1SC(s,0)S(0,t)，?s,t≥0，

則由引理1得算子A+B生成雙參數n階α次積分C半群{S(s,t)}s,t≥0。

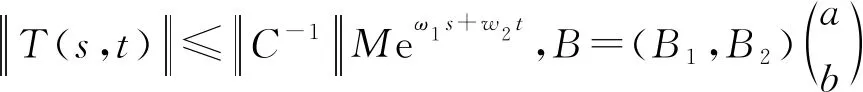
VT(s,t)=

(1)

證明令V0(s,t)=T(s,t)，定義

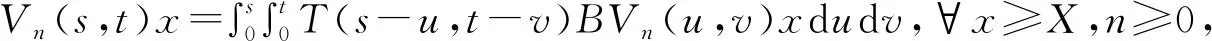
有(s,t)→V(s,t)x連續。

下面利用數學歸納法證明。

||Vn(s,t)||≤

(2)

當n=0，顯然||V0(s,t)||≤||C-1||Meω1s+w2t成立：

假設取n時有

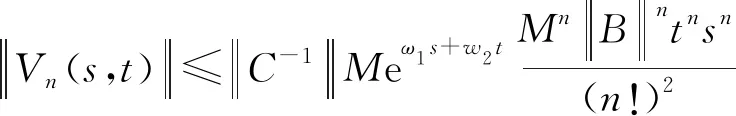
當取n+1時，

||Vn+1(s,t)x||=

||C-1||2Mn+2||B||n+1eω1s+w2t||x||·

所以對于?x>0有

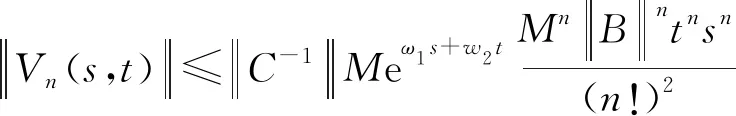
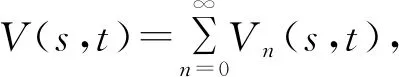
(3)

由(2)式得(3)式在任意有界區間上相當于一致算子拓撲是一致連續的，所以對于?x≥X，都有(3)式成立。

下面證明唯一性：設對于?s,t≥0,當x∈[0,+∞),(s,t)→V(s,t)x是連續的，且有

則||V(s,t)x-U(s,t)x||≤

||V(u,v)x-U(u,v)x||dudv。

又由||V(s,t)x-U(s,t)x||=0，所以，對于?s,t≥0,V(s,t)x=U(s,t)x。

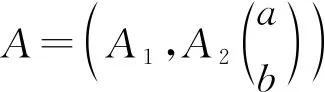
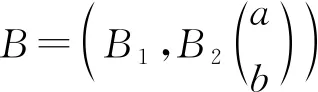
||S(s,t)x-S(s,t)x||≤

證明由定理1和推論1得

||S(s,t)x-S(s,t)x||≤

||S(u,v)||||x||dudv≤

Me(ω1+M‖B‖)u+(ω2+M‖B‖)v||x||dudv=