基于空氣動(dòng)力學(xué)的旋轉(zhuǎn)球體飛行軌跡的計(jì)算模擬
趙炳炎 陳宗華
(玉林師范學(xué)院物理與電信工程學(xué)院,廣西 玉林 537000)
在大學(xué)物理課程中,斜拋問題常被用來作為實(shí)例進(jìn)行分析,分析時(shí)一般會(huì)把運(yùn)動(dòng)軌跡局限在豎直的平面內(nèi),并且將研究對(duì)象作為質(zhì)點(diǎn),根據(jù)牛頓定律分別在豎直和水平兩個(gè)方向上建立動(dòng)力學(xué)方程,有時(shí)還可以將空氣的阻力考慮進(jìn)來,最終得到兩個(gè)獨(dú)立的二階線性常微分方程,求解可得出該斜拋運(yùn)動(dòng)的軌跡、最大射程、飛行時(shí)間等信息,這類問題已經(jīng)成為質(zhì)點(diǎn)動(dòng)力學(xué)的經(jīng)典例題。然而,從學(xué)以致用的角度出發(fā),還有一些類斜拋問題受到廣大學(xué)生的關(guān)注,比如足球運(yùn)動(dòng)中的“香蕉球”和棒球運(yùn)動(dòng)中“詭異的弧線球”等,這些現(xiàn)象顯然與大學(xué)物理課程中學(xué)的斜拋運(yùn)動(dòng)是不符的。旋轉(zhuǎn)的球體在飛行時(shí),不僅受空氣阻力的影響,還需考慮由旋轉(zhuǎn)而引起的馬格努斯力。但是由于旋轉(zhuǎn)球體與空氣的相互作用較為復(fù)雜,且動(dòng)力學(xué)方程無法直接求得解析解,以往的討論往往都局限在定性的描述或者簡單分析二維的情況[1-5]。
本文通過對(duì)斜拋的飛行球體進(jìn)行簡化建模,將球體簡化成質(zhì)點(diǎn)并建立動(dòng)力學(xué)方程,借助Matlab軟件利用龍格庫塔法對(duì)方程進(jìn)行編程求數(shù)值解,從而模擬出球體的飛行軌跡。方程在三維空間建立,所以可以模擬出球體任意方向、任意旋轉(zhuǎn)情況的飛行軌跡。這不但可以更好地幫助學(xué)生理解復(fù)雜曲線運(yùn)動(dòng),還可以幫助專業(yè)體育教練指導(dǎo)球類運(yùn)動(dòng)訓(xùn)練。
1 旋轉(zhuǎn)球體在空氣中運(yùn)動(dòng)的動(dòng)力學(xué)特征
球體在飛行過程中除了受到重力作用,還與空氣有相互作用。其中重力作用的大小和方向都不變,記為mg,方向豎直向下。需要討論的是球體與空氣的相互作用,這涉及空氣動(dòng)力學(xué)問題,比較復(fù)雜,需要建模簡化。可以將球體與空氣的相互作用簡化為空氣浮力(該力方向始終豎直向上,可以歸化到重力mg)、空氣阻力FD和由旋轉(zhuǎn)而產(chǎn)生的馬格努斯力FM,其受力情況如圖1所示。
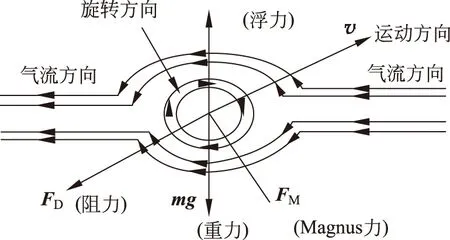
圖1 飛行球體受力圖
1.1 對(duì)空氣阻力的分析
由于球體的對(duì)稱性,空氣阻力FD與速度方向相反,空氣阻力FD與球飛行速度的關(guān)系可以通過簡化建模得到,如圖2所示的圓盤為球體最大截面并與速度方向正交。
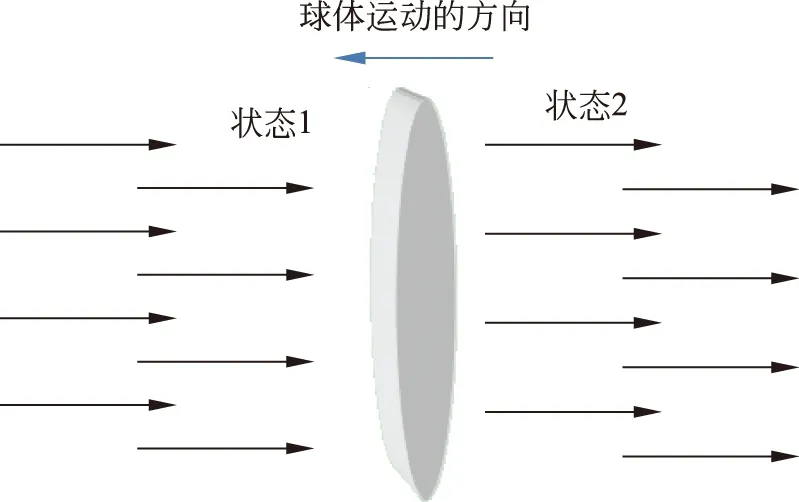
圖2 圓盤兩面氣流情況圖
如圖2,圓盤兩面所受到的壓力不同,狀態(tài)1為氣流還未被球體穿過,壓強(qiáng)為p1,相對(duì)流速v1=v。狀態(tài)2的氣流完全被圓盤遮擋,壓強(qiáng)p2,相對(duì)流速v2=0。根據(jù)伯努利原理可得:
(1)
根據(jù)式(1),可以得到截面兩邊的壓力差為
(2)
令圓盤面積為S,圓盤所受的阻力為圓盤兩面的壓力差:
(3)
式(3)是球體建模簡化后的阻力關(guān)系公式。實(shí)際的球體并不是圓盤,空氣會(huì)有速度損失,空氣流過球體表面時(shí)會(huì)有摩擦力,而且球體旋轉(zhuǎn)也會(huì)對(duì)球體阻力產(chǎn)生影響,實(shí)際的情況更加復(fù)雜[6-8]。本文引入空氣阻力常數(shù)Cd來歸化這些影響,在文獻(xiàn)[6]~[8]中已經(jīng)指出Cd不但與球體材料和表面結(jié)構(gòu)有關(guān),還與球飛行速度和轉(zhuǎn)動(dòng)速度有關(guān),但是在本文中作為教學(xué)討論,我們可以令系數(shù)Cd為一個(gè)常數(shù),空氣阻力可以表示為
(4)
其中,S為球體的最大截面;ρ為空氣密度;為球的速度。如果空氣密度不變,不考慮球體變形,則空氣阻力只與速度的平方成正比,方向始終與速度方向相反。
1.2 對(duì)球體旋轉(zhuǎn)引起的馬格努斯效應(yīng)的分析
球體旋轉(zhuǎn)產(chǎn)生的馬格努斯力來自于球體的各面流速不同所導(dǎo)致的壓強(qiáng)差,這里以旋轉(zhuǎn)軸方向與球速方向垂直為例,如圖3所示。
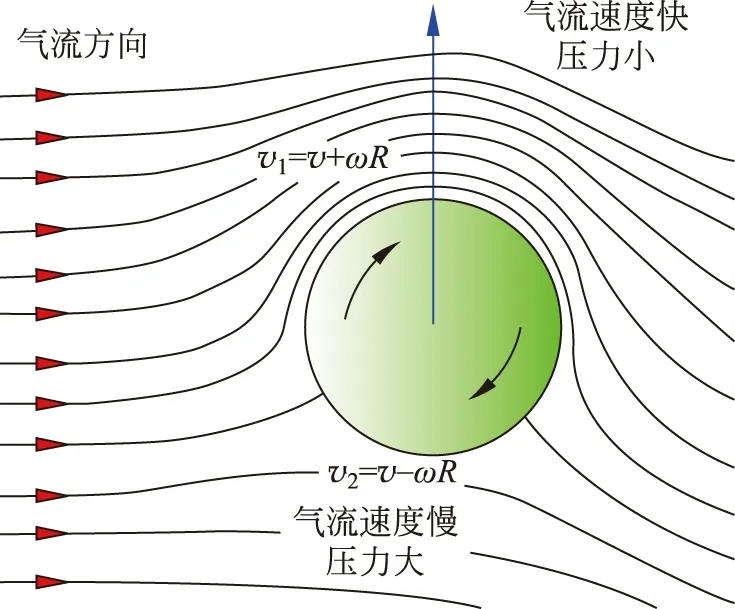
圖3 馬格努斯力示意圖
旋轉(zhuǎn)的球體在空氣中飛行時(shí),旋轉(zhuǎn)方向迎著氣流一面的流速減慢,而順著氣流一面的流速加快,根據(jù)伯努利方程:
(5)
兩面的壓力差產(chǎn)生一個(gè)垂直于ω和的馬格努斯力,其大小為
(6)
可以引入系數(shù)Cl使馬格努斯力的表達(dá)形式與式(4)一致,并將馬格努斯力的方向FM~ω×考慮進(jìn)來,則有
(7)
式(7)中系數(shù)Cl的大小與球體表面結(jié)構(gòu)、空氣黏度、空氣密度、飛行速度和旋轉(zhuǎn)速度都有關(guān)[6-8]。為了不引起學(xué)生們的困惑,將它設(shè)為一個(gè)常數(shù)。
2 建立球體飛行的動(dòng)力學(xué)方程
首先建立三維直角坐標(biāo)系Oxyz,其中x軸和y軸為水平方向,z軸為豎直方向,根據(jù)牛頓第二定律建立球體飛行的動(dòng)力學(xué)方程:
(8)
飛行過程中,角速度的方向可以分別投影到三維坐標(biāo)軸上,有:
(9)
其中,
(10)
將球體動(dòng)力學(xué)方程分解到各坐標(biāo)軸方向上,得到3個(gè)二階常微分方程:
(11)
其中,
(12)
該二階常微分方程組是無法直接求得解析解的,需要用數(shù)值分析的方式來求數(shù)值解。我們采用Matlab軟件包中四階龍格庫塔算法函數(shù)ode45對(duì)該方程組進(jìn)行降階計(jì)算。龍格庫塔法求數(shù)值解必須給出初始條件,這里考慮球體在xz平面內(nèi)由坐標(biāo)原點(diǎn)出射,并假設(shè)球體射出后角速度ω保持不變。
3 以上、下旋和側(cè)旋為例,得出軌跡圖
在進(jìn)行課堂討論的時(shí)候,可以選擇學(xué)生們比較感興趣的足球進(jìn)行討論,相關(guān)參數(shù)設(shè)定可以在課堂上與學(xué)生們共同討論得到。
設(shè)球體質(zhì)量m=0.4kg,空氣密度為ρ=1.29kg/m3,球體的最大截面積S=0.03m2,空氣阻力常數(shù)Cd=0.35,升力系數(shù)為Cl=0.18。
為了方便討論,設(shè)足球以45°在xz平面內(nèi)踢出,踢出后的旋轉(zhuǎn)角速度方向,分別以上旋、下旋和側(cè)旋的情況進(jìn)行討論。
3.1 上、下旋的情況
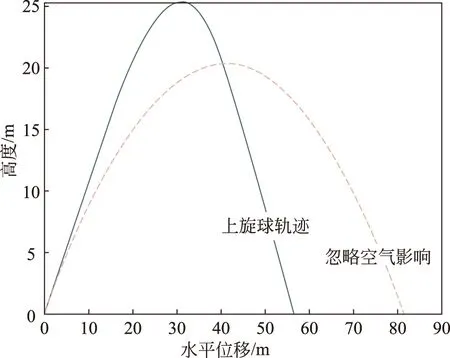
圖4 足球上旋時(shí)的飛行軌跡圖

圖5 足球下旋時(shí)的飛行軌跡圖
從圖4和圖5的對(duì)比可以明顯看到,空氣阻力使得足球飛行的距離明顯減小。但是上旋時(shí)的馬格努斯力方向豎直向上,相當(dāng)于抵消了一部分重力作用,足球飛行的距離較高。而下旋球受到的馬格努斯力方向豎直向下,相當(dāng)于加大了重力作用,足球飛行高度較低,甚至比上旋球低了近15m。由于上旋球在空中飛行的時(shí)間較長,所以水平飛行的距離也比下旋球要多出約12m,但是無論是上旋球還是下旋球的飛行距離,都明顯比忽略空氣影響時(shí)的距離要小得多。這也說明足球在飛行過程中,空氣阻力和馬格努斯力對(duì)飛行軌跡的影響非常大。
3.2 側(cè)旋球的情況
側(cè)旋情況是指,球體旋轉(zhuǎn)角速度ω的方向與球體初始射出方向垂直,與速度方向順時(shí)針成90°時(shí)定義為右旋,與速度方向逆時(shí)針成90°時(shí)定義為左旋,其他初始條件與3.1一致。
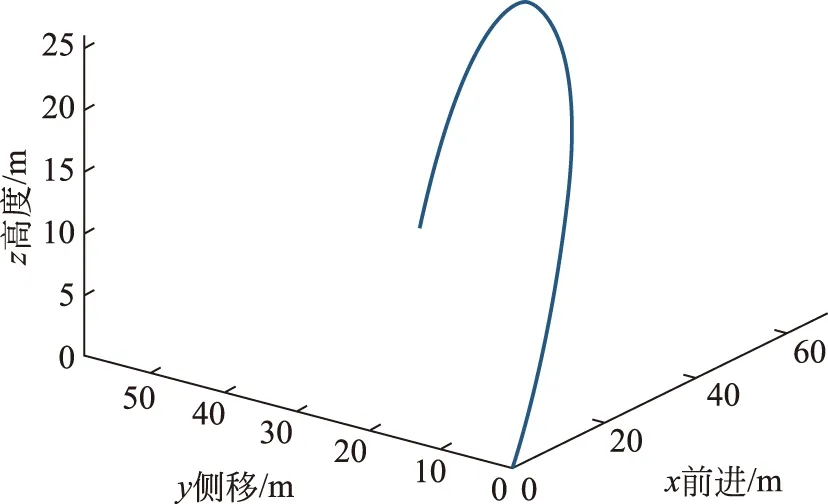
圖6 足球右旋射出后的飛行軌跡
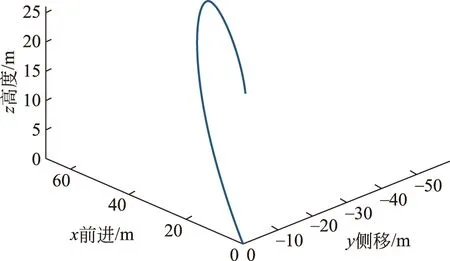
圖7 足球左旋射出后的飛行軌跡
從圖6和圖7可以看到,由于足球旋轉(zhuǎn)產(chǎn)生的馬格努斯力,讓足球飛行的軌跡發(fā)生了明顯的偏轉(zhuǎn):右旋會(huì)讓足球向左邊偏轉(zhuǎn),左旋會(huì)讓足球向右邊發(fā)生偏轉(zhuǎn),這就是足球里經(jīng)常說的“圓月彎刀”或者“香蕉球”。但是需要說明的是,實(shí)際情況中球體的旋轉(zhuǎn)同樣會(huì)受到空氣阻力使角速度變小,而系數(shù)Cl和Cd也會(huì)發(fā)生一定的變化,所以實(shí)際上的偏轉(zhuǎn)不會(huì)有這么大。
由圖8可以看到完全的左右側(cè)旋球在xz平面內(nèi)的軌跡是一樣的,這是因?yàn)閭?cè)旋時(shí)的馬格努斯力是完全垂直于該平面的,它只能讓球飛行發(fā)生轉(zhuǎn)彎,產(chǎn)生所謂的“香蕉球”,而在球體前進(jìn)方向上,只有空氣阻力的作用,飛行距離一致。
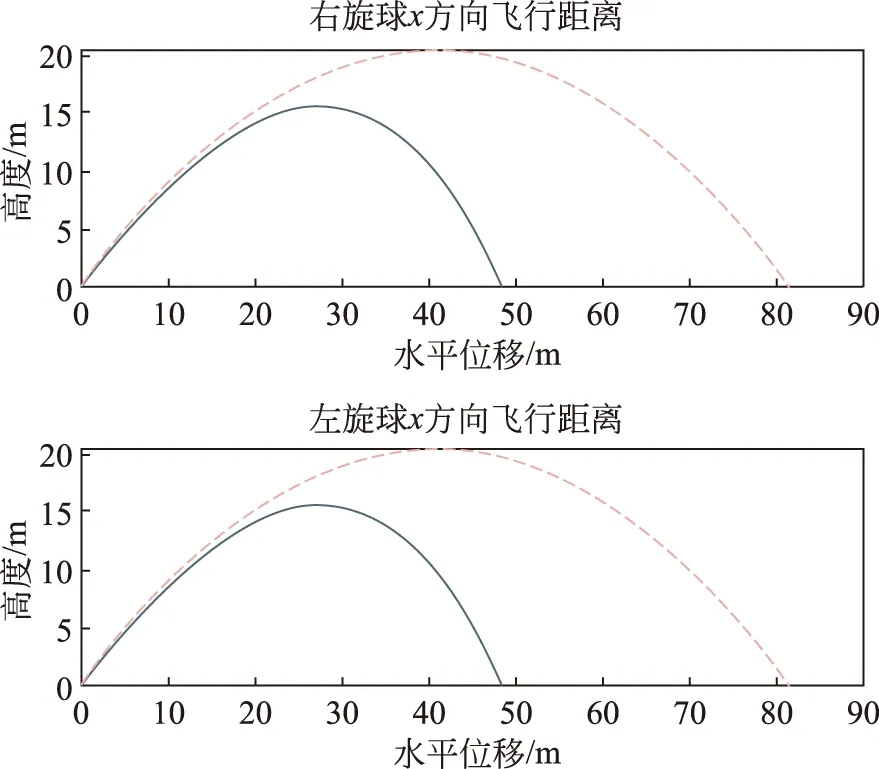
圖8 側(cè)旋球在xz平面內(nèi)的飛行軌跡
4 結(jié)語
將貼近大學(xué)生生活的體育運(yùn)動(dòng)案例融入大學(xué)物理教學(xué),既可以提升他們的興趣,還可以培養(yǎng)他們應(yīng)用物理理論分析問題和解決問題的能力。本文將飛行的旋轉(zhuǎn)球體與空氣的相互作用簡化成一個(gè)空氣阻力和一個(gè)馬格努斯力,并將球體簡化成質(zhì)點(diǎn)模型建立動(dòng)力學(xué)方程,且借助Matlab軟件編程求解。以足球?yàn)槔?jì)算模擬了足球上、下旋和側(cè)旋的飛行軌跡,發(fā)現(xiàn)空氣對(duì)旋轉(zhuǎn)球體飛行軌跡的影響很大,這與足球運(yùn)動(dòng)時(shí)的實(shí)際情況基本相符。當(dāng)然實(shí)際的球體飛行時(shí),只有質(zhì)點(diǎn)的動(dòng)力學(xué)方程是不夠的。球體本身還有旋轉(zhuǎn),而且這個(gè)旋轉(zhuǎn)是可以繞任意轉(zhuǎn)軸的,且球體旋轉(zhuǎn)的變化也會(huì)導(dǎo)致空氣阻力和馬格努斯力的變化。要更準(zhǔn)確地模擬出球體飛行的軌跡,有待更深入的討論。

