輕重物體系繞桿運動的循環擺現象研究
曾溢嘉,王曉杰,李文華,陳宗強
(南開大學 物理科學學院,天津 300071)
第32屆國際青年物理學家錦標賽(IYPT)的第14題[1]為: Connect two loads, one heavy and one light, with a string over a horizontal rod and lift up the heavy load by pulling down the light one. Release the light load and it will sweep around the rod, keeping the heavy load from falling to the ground. Investigate this phenomenon. 本題要求對輕物如何通過掃動阻礙重物落向地面的過程進行研究. 本文結合力學分析與模擬,研究了輕物的掃動軌跡與重物的下落過程.
1 理論分析
1.1 重物下落過程
循環擺系統主要由一輕一重兩物體(質量分別為m和M)、水平桿(半徑R)和輕質繩構成. 將輕重兩物體簡化為質點,將繩簡化為不會伸長、無質量的理想繩,并忽略空氣阻力[2-3]. 兩物體質量比定義為:k=m/M. 如圖1所示,其中,A表示輕物體端繩與桿的切點,r表示輕物體m到切點A的距離,θ表示輕物體端繩與軸夾角,R表示桿的半徑,z表示重物體M到重物體端繩與桿的切點的距離,T和T′分別表示輕重物體端繩上的拉力. 以桿中心O為原點建立直角坐標系xOy(簡稱坐標O系),再以輕物體端繩與桿的切點A為原點建立直角坐標系x′Ay′(簡稱坐標A系).
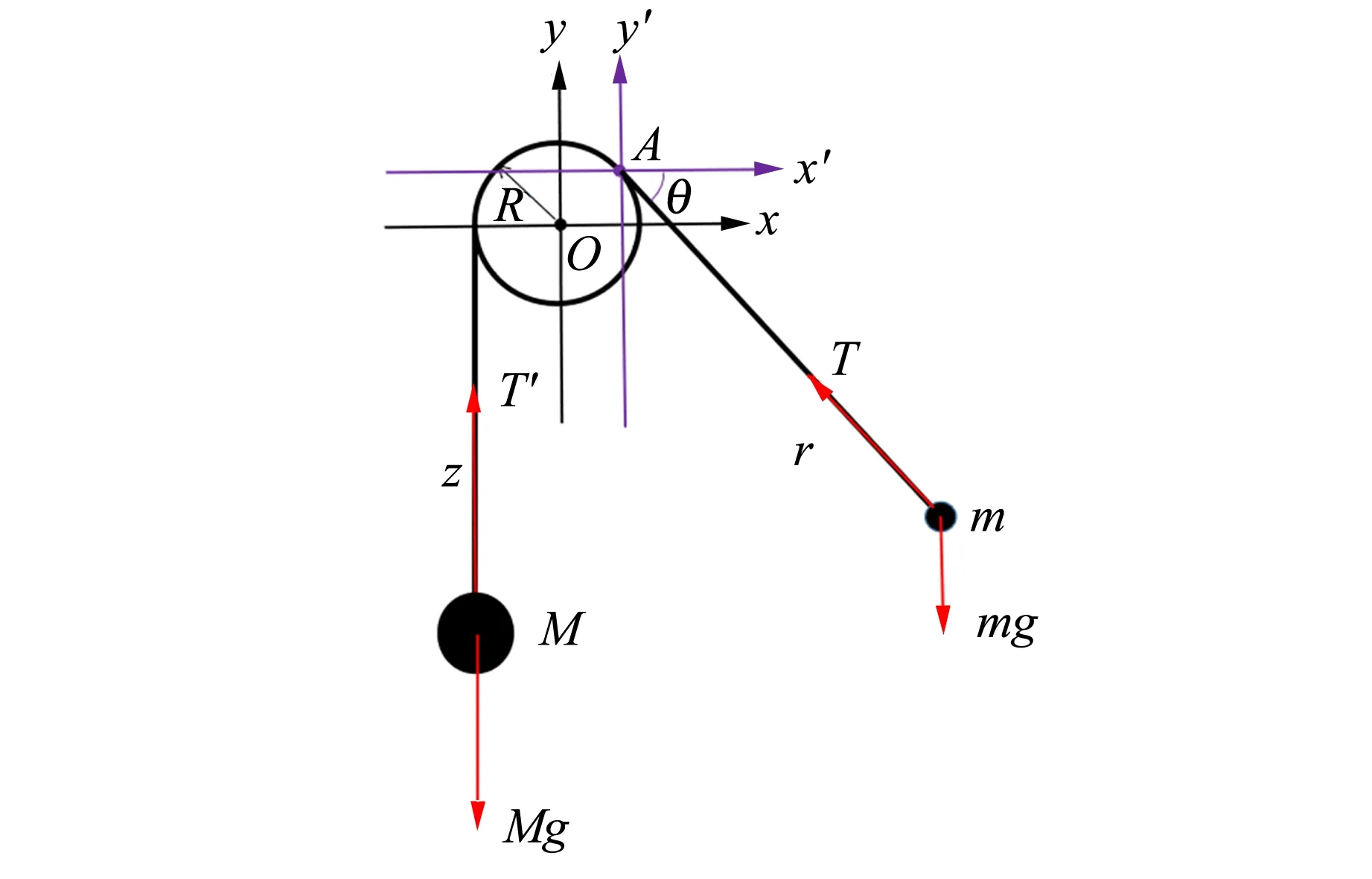
圖1 循環擺結構示意圖
先分析A點相對O點的運動,根據圖2(a)所示的A點運動示意圖,可以算出A點相對于O點的運動速度為
(1)
因此,A點相對O點的徑向和切向加速度分別為
ar=Rω2,
(2)
(3)
其方向如圖2(b)所示.
對輕物體進行受力分析,如圖3所示,其中mar,maτ表示由A點相對于O點運動引起的慣性力. 根據牛頓運動定律,輕物體在坐標A系水平方向與豎直方向的運動方程分別為[4]
(4)
(5)
其中,θ滿足:
(6)
(7)
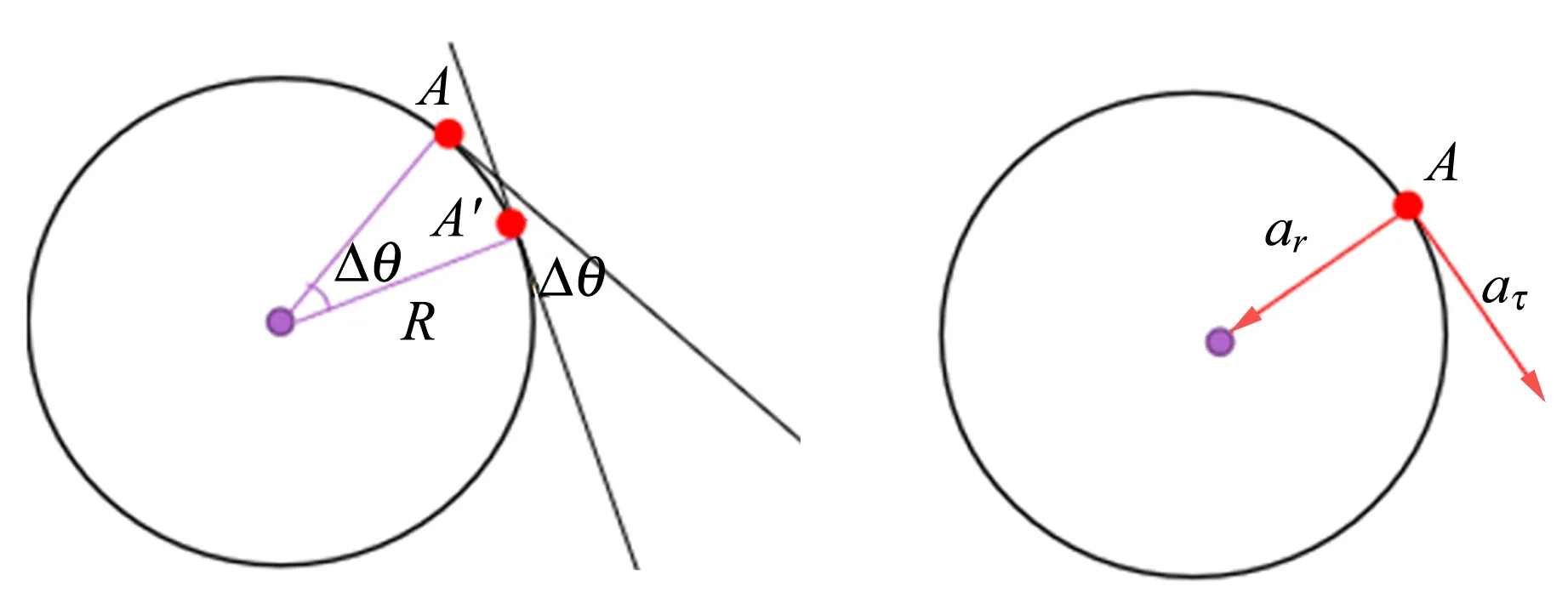
(a)A點運動 (b)A點對地加速度 圖2 A點運動及對地加速度示意圖

圖3 A系中輕物體受力分析示意圖
現在需要在坐標O系中求得T的表達式. 如圖1所示,在坐標O系中,根據牛頓運動定律,在沿繩方向上有:
ma=T-mgsinθ,
(8)
加速度a可以由圖1中幾何關系求得:
(9)
其中,r0和θ0分別表示t=0時刻r和θ初始值,即輕物體端原始繩長和釋放時輕物體端繩與x′軸夾角.
將式(9)代入式(8)中,得到T的表達式為
(10)
對于重物體端受力進行分析,其運動方程為

(11)
根據文獻[5-6],取桿上線元進行受力分析再積分,對輕繩兩端的張力有:
(12)
其中,μ為繩與桿之間的摩擦系數. 分別令r0和z0為輕物體端和重物體端原始繩長,在總繩長不變的前提下,任意時刻的繩長滿足:
(13)
聯立式(11)~(13),可以得到重物體在豎直方向的運動方程為
(14)
綜上,將式(6),(7),(10)和式(14)代入式(4)和式(5)中,得到在A系中輕物體m的運動微分方程. 利用O和A兩系坐標的轉換關系:
x=x′+Rsinθ,
(15)
y=y′+Rcosθ,
(16)
得到坐標O系(即地面系)中物體的運動方程.
1.2 重物體靜止時
重物體靜止時,輕物體的運動受到幾何條件的約束. 在坐標A系中,輕物體m相對于A點的力矩為
(17)
此時,拉力T依然滿足式(7),只不過此時由重物體運動引起的加速度變為0,即
(18)
建立如圖4所示的θ-r極坐標系,其中r表示輕物體m到切點A的距離,θ表示輕物體端繩與水平方向夾角,L表示輕物體到過A點豎直線的距離,R表示桿的半徑. 物體所受幾何約束可以表示為

圖4 坐標A系中輕物體受力分析示意圖
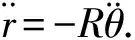
(19)
式(17)和式(19)聯立,即是A系中輕物體運動的微分方程,再由O和A兩系坐標的轉換關系式(15)和式(16),得到O系中物體的運動方程.
1.3 重物體運動與靜止的臨界條件
2 仿真模擬
2.1 輕重物體的質量比對循環擺運動的影響
固定β=90°,r0=0.628 m,μ=0.23,R=4.85 mm,逐漸增大輕重物質量比k,繪出輕物的運動軌跡. 圖5為模擬結果中具有代表性的幾例軌跡,分別對應了在不同初始條件下,循環擺現象中可能出現的不同情況:
1)當質量比k較小(0.10)時,重物體經過1次下落之后不再運動,直到輕物體端繩長減小到0. 圖5(a)所示的運動軌跡是最典型的循環擺運動曲線.
2)當質量比k逐漸增大時(臨界值~0.24),重物體在整個過程中會出現2次下落,最終輕物體端繩長收縮到0,如圖5(b)所示. 這是由于在運動過程中質量比k較大,導致輕物體速度較小,無法產生足夠的拉力,從而引起重物體再次下落.
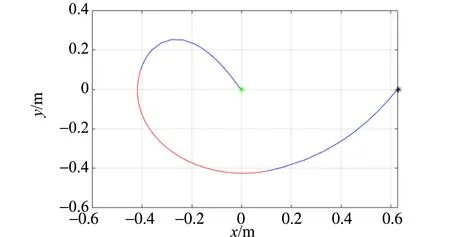
3)當質量比k增大到臨界值時(0.34),輕物體會在輕物體端繩長不為0時與桿發生碰撞,從而輕物體被桿彈回,同時,重物體直接落向地面. 圖5(c)為輕物能否阻礙重物體落向地面的臨界情況.
4)當質量比k大于臨界值時,輕物體的速度將無法支持其繼續向上運動,回蕩下來,而重物體直接落向地面. 圖5(d)所示的軌跡是無法阻礙重物體下落的最常見情況.

(a)k=0.10

(b)k=0.25
(c)k=0.34
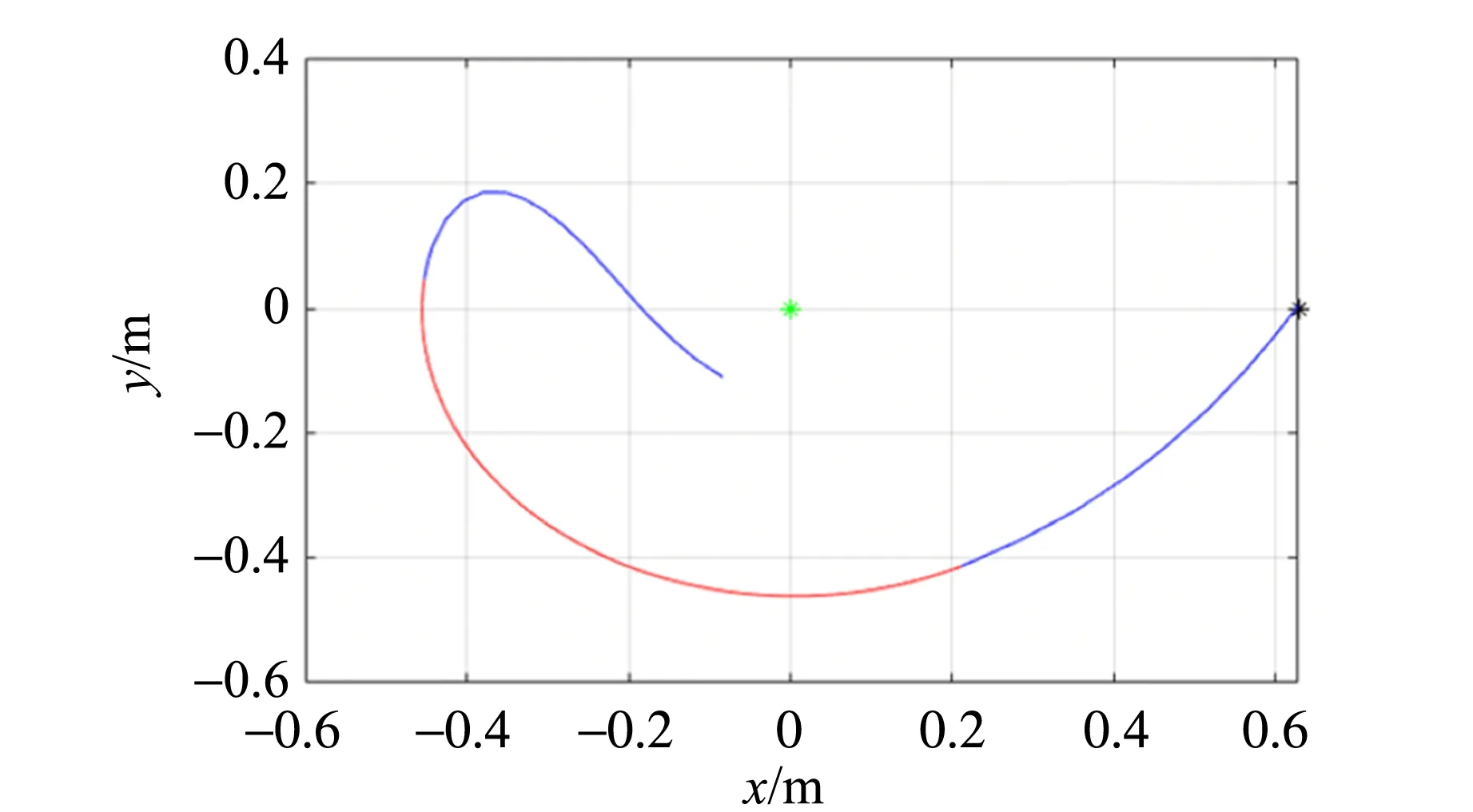
(d)k=0.50圖5 不同質量比k時輕物體的運動軌跡(藍色段表示重物體在下落,紅色段表示重物體處于靜止)
經大量數據模擬后,發現在質量比k小于臨界值(一般在0.27~0.43,取決于其他初始條件)時,隨著質量比k的增大,輕物體會越來越難以阻礙重物體的下落,并會出現多次下落. 在k值達到臨界值以上之后,輕物體將不能完成繞桿掃動,也無法阻礙重物體下落至地面.
2.2 釋放角度比對循環擺運動的影響
固定k=0.30,r0=0.628 m,μ=0.23,R=4.85 mm,改變β,模擬結果如圖6所示.
1)當釋放角度為90°時,輕物體可以完成繞桿掃動1周,最終阻礙重物體下落,如圖6(a)所示.
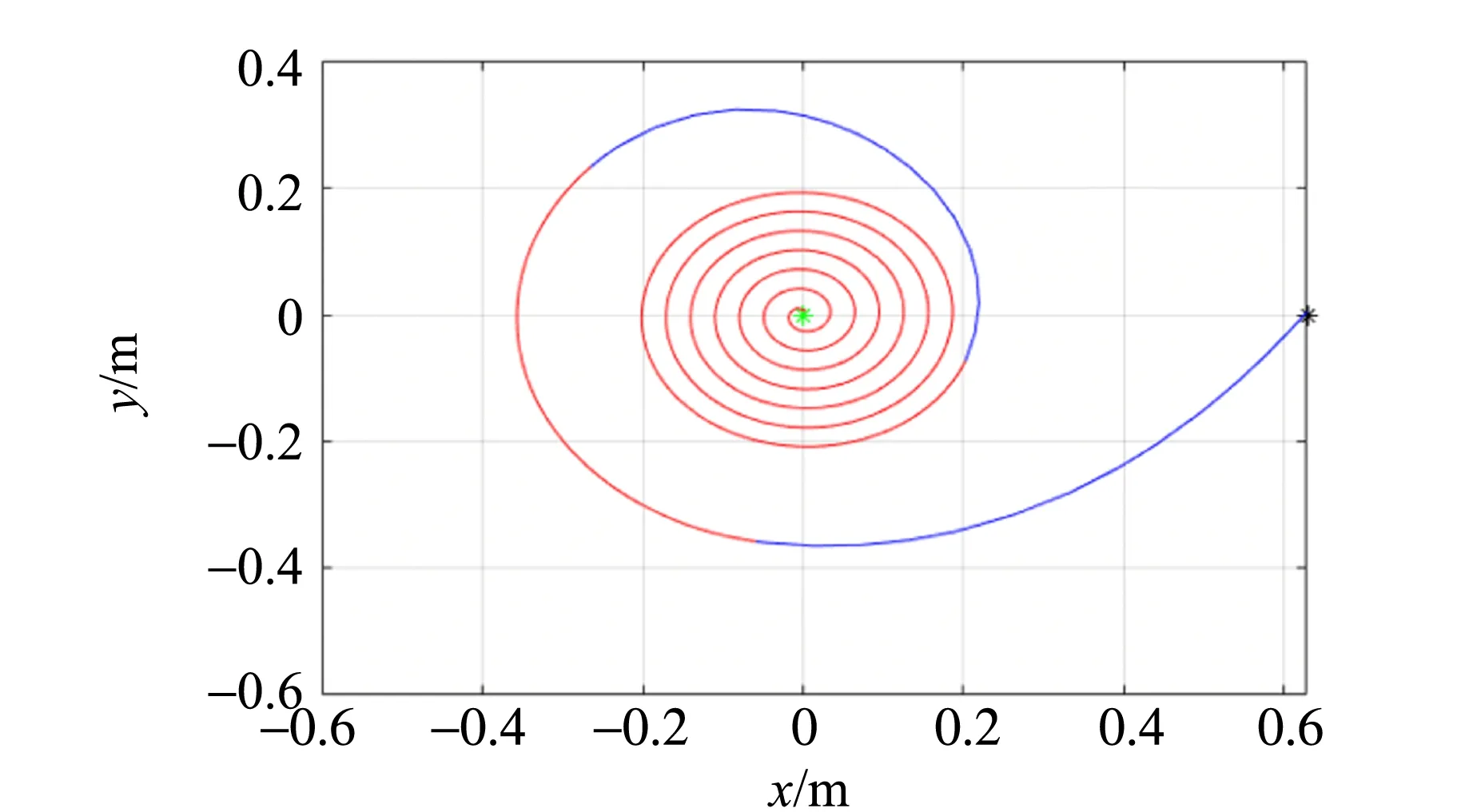
(a)β=90°
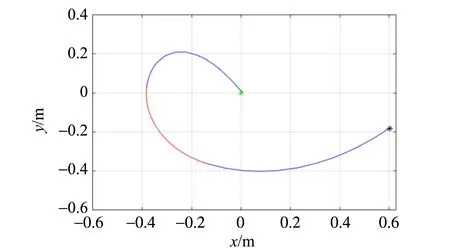
(b)β=73°

(c)β=70°圖6 不同輕物體釋放角度下輕物體的運動軌跡(藍色段表示重物體在下落,紅色段表示重物體處于靜止)
2)當釋放角度為73°時,輕物體會在輕物體端繩長不為0時與桿發生碰撞,從而輕物體被彈回,重物體直接落向地面,如圖6(b)所示.
3)當釋放角度為70°時,輕物體的速度不支持輕物體繞桿1周,最終輕物體蕩回,重物體落向地面,如圖6(c)所示.
經過大量的數值模擬,發現釋放角度越小,輕物體越難以阻礙重物體的下落. 當釋放角度減小到臨界值(一般在68°~90°,取決于其他初始條件,未考慮90°以上的情況)后,輕物體不能完成繞桿掃動,也無法阻礙重物體落向地面.
2.3 繩長對循環擺運動的影響
固定k=0.10,β=90°,μ=0.23,R=4.85 mm,改變初始繩長r0,輕物的運動軌跡結果如圖7所示,可以看出繩長的改變并不會對輕物體曲線與重物體下落造成顯著影響.

(a)r0=0.428 m
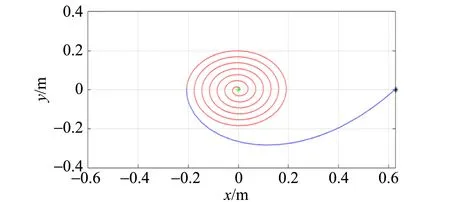
(b)r0=0.628 m圖7 不同初始繩長下輕物體的運動軌跡(藍色段表示重物體在下落,紅色段表示重物體處于靜止)
2.4 摩擦系數對循環擺運動的影響
取k=0.10,β=90°,r0=0.628 m,R=4.85 mm,改變摩擦系數μ,探究其對輕物體運動軌跡的影響.
不同摩擦系數μ下輕物體的運動軌跡如圖8所示. 其中μ=0.23時用綠色和黑色曲線表示,其中綠色部分表示重物體在下落,黑色部分表示重物體處于靜止;μ=0.53時用藍色和紅色曲線表示,其中藍色部分表示重物體在下落,紅色部分表示重物體處于靜止. 從圖8中可以發現,隨著μ的增大,曲線向外擴張. 通過比較綠色與黑色曲線長度,發現在μ較大時,下落距離明顯減小.
當μ=1.00,循環擺出現擺回現象. 輕物體運動軌跡如圖9所示,即輕物體繞桿1周后速度不能支撐其做第2次繞桿,這是由于μ太大,重物體下落距離減小,輕物體速度過慢. 雖然輕物體無法再次完成繞桿運動,但并不妨礙其借助繩與桿之間的摩擦力阻礙重物體落向地面,這種情況下,仍然認為其完成了循環擺現象.
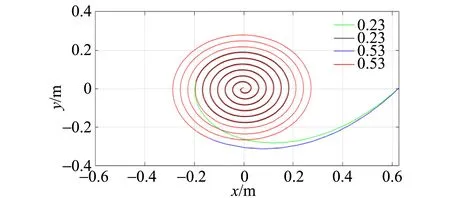
圖8 不同摩擦系數μ下輕物體的運動軌跡
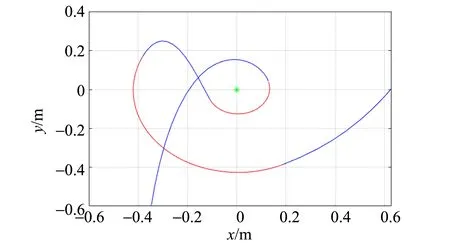
圖9 μ=1.00時輕物的運動軌跡(藍色部分表示重物體在下落,紅色部分表示重物體處于靜止)
2.5 桿半徑對循環擺運動的影響
取k=0.10,β=90°,r0=0.628 m,μ=0.23,改變桿半徑R,探究其對輕物體運動軌跡的影響.
圖10為不同桿半徑R下輕物體的運動軌跡,R=0.003 m時用綠色和黑色曲線表示,其中綠色部分表示重物體在下落,黑色部分表示重物體處于靜止;R=0.005 m時用藍色和紅色曲線表示,其中藍色部分表示重物體在下落,紅色部分表示重物體處于靜止. 從圖10中可以發現,桿半徑R較大時,重物體下落階段軌跡并不會發生明顯變化,這是由于這一階段θ的變化往往不大導致的. 而對于θ明顯變化的重物體靜止階段,R較大對應的運功軌跡處于內側.
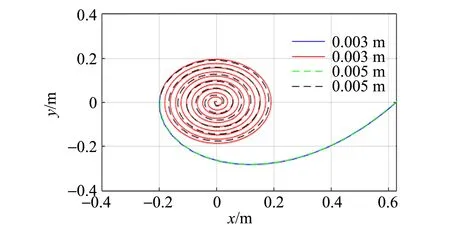
圖10 不同桿半徑R下輕物體的運動軌跡
3 實驗研究
為了驗證數值模擬的結果,實驗使用高速攝像機記錄循環擺輕物的運動過程,再用Tracker軟件進行打點分析. 實驗中所使用的攝像機為高速相機FDR-AX700,拍攝幀率為120幀. Tracker軟件版本為5.1.0. 繩長、角度用Tracker定標測量的方法(長度定標尺精度為1 mm,角度定標尺精度為0.1°),桿直徑用游標卡尺測量(精度0.02 mm),輕重物體的質量用電子稱測量(精度0.01 g),實驗裝置如圖11所示. 實驗得到細繩和桿的摩擦系數μ=0.230和桿半徑R=4.85 mm.

圖11 實驗裝置圖
3.1 輕物體的運動軌跡
首先,記錄能阻礙重物體落向地面時不同實驗條件下輕物體的運動軌跡. 實驗結果如圖12所示,黑色曲線為實驗軌跡,藍色曲線和紅色曲線表示理論運動軌跡,藍色曲線為重物體下落過程輕物體的軌跡,紅色曲線表示重物體處于靜止時輕物體的軌跡.

(a)k=0.096,β=93.9°,r0=0.587 m
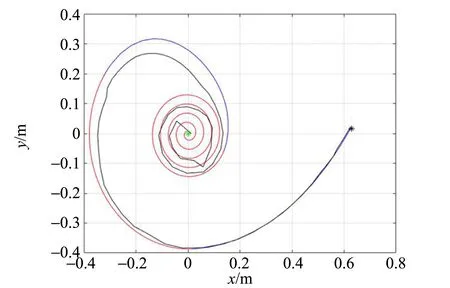
(b)k=0.326,β=91.5°,r0=0.628 m

(c)k=0.400,β=92.7°,r0=0.525 m圖12 實驗過程中輕物體運動軌跡與理論軌跡對比
圖12(a)為重物下落1次情況,圖12(b)為重物下落2次及以上的情況,圖12(c)為能阻礙重物體下落的臨界情況. 可以發現,對于各種能阻礙重物體落向地面的情況,輕物體運動軌跡與理論仿真軌跡都符合得較好.
3.2 重物體運動速度
首先研究重物體第1次下落過程的速度變化圖,理論曲線與實驗曲線擬合結果如圖13所示,可以看出,在重物體第1次下落過程中,開始輕物體端重力沿繩方向分量較小,可近似為重物體拉著輕物體以加速度
下落,之后隨著角度θ的增大,輕物端拉力與摩擦力的合力逐漸變大,當增大到大于重物重力時,重物體開始減速下落,最后停止運動.
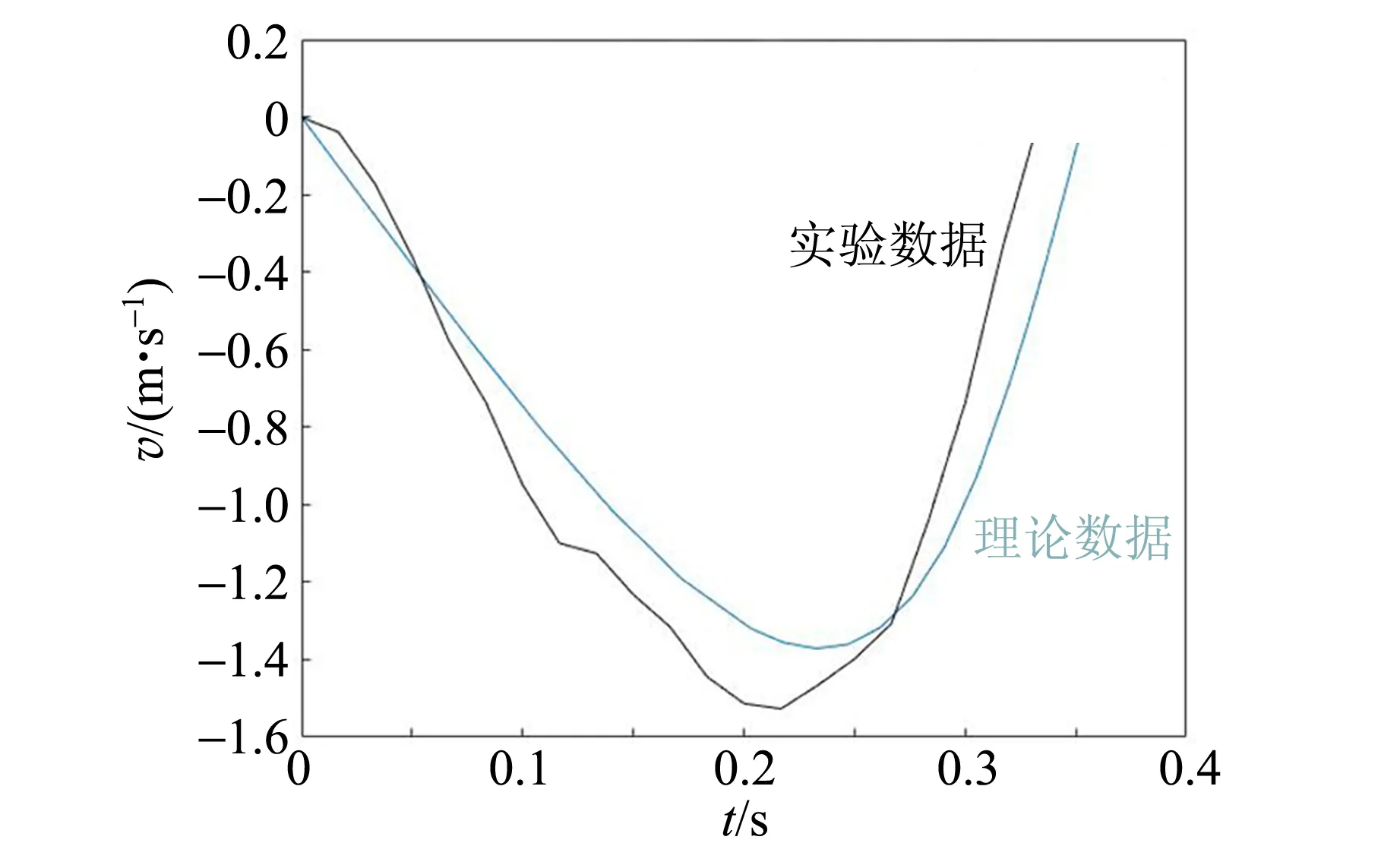
(a)k=0.195,r0=0.571 m,β=93.1°
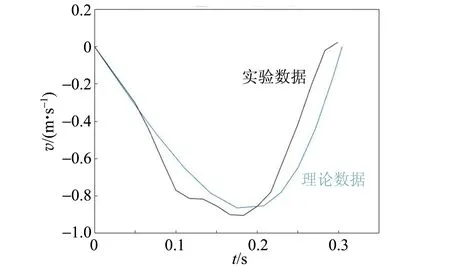
(b)k=0.120,r0=0.525 m,β=92.7°圖13 不同實驗條件下重物體下落過程的速度變化
3.3 重物體的運動時間
研究了可以形成循環擺過程中,β,r0及k對重物體從開始下落到停止所持續時間Δt的影響. 實驗結果與理論結果如圖14~16所示. 可以看出,釋放角度β越大,初始繩長r0越短,重物體下落持續時間Δt越短. 在質量比k較小時,質量比對下落時間的影響并不顯著,在質量比較大時,質量比越大,下落時間Δt越短.
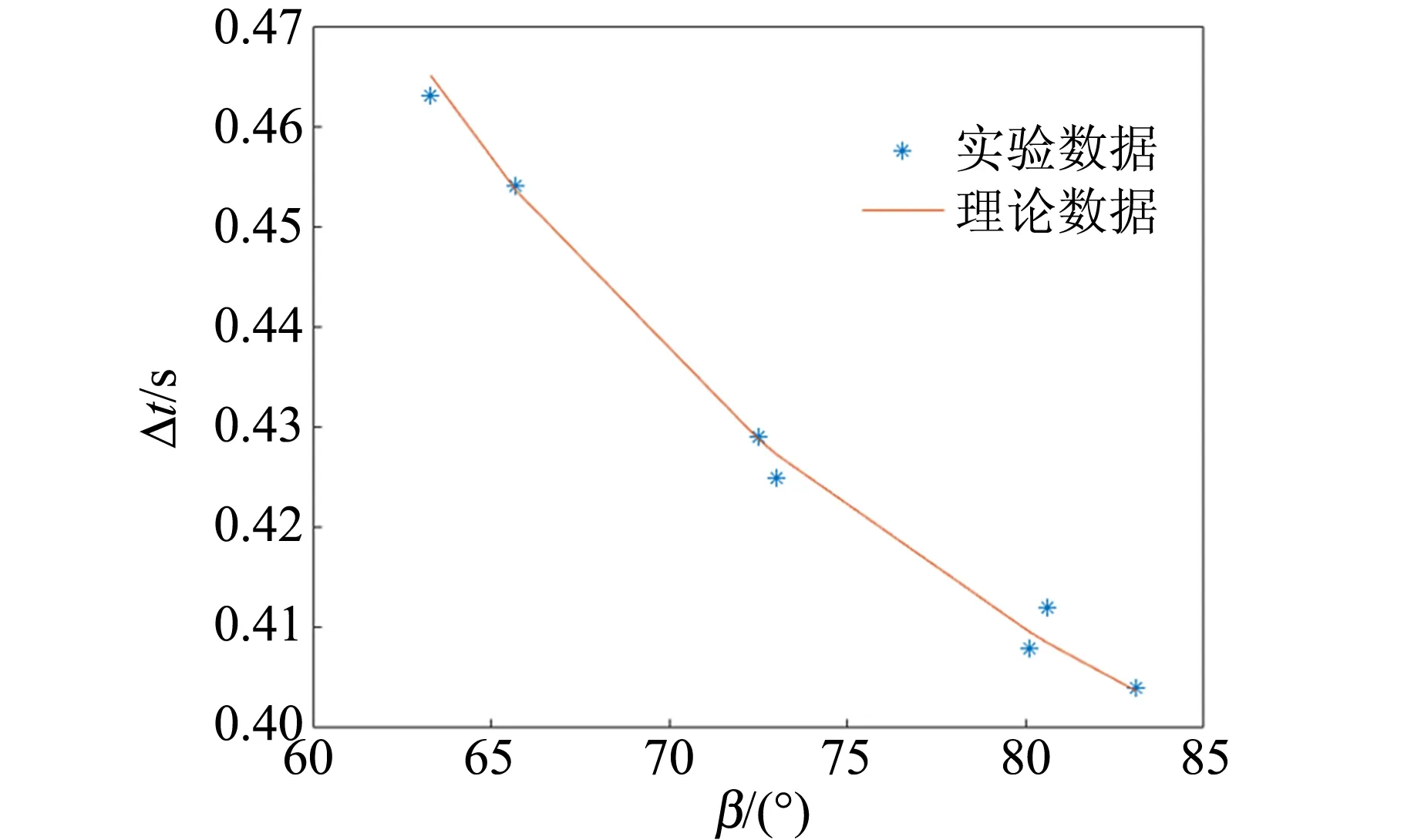
圖14 Δt與β的關系(R=4.85 mm,μ=0.192,r0=0.703 m,k=0.250)

圖15 Δt與r0的關系(R=4.85 mm,μ=0.192,β=92.3°,k=0.250)
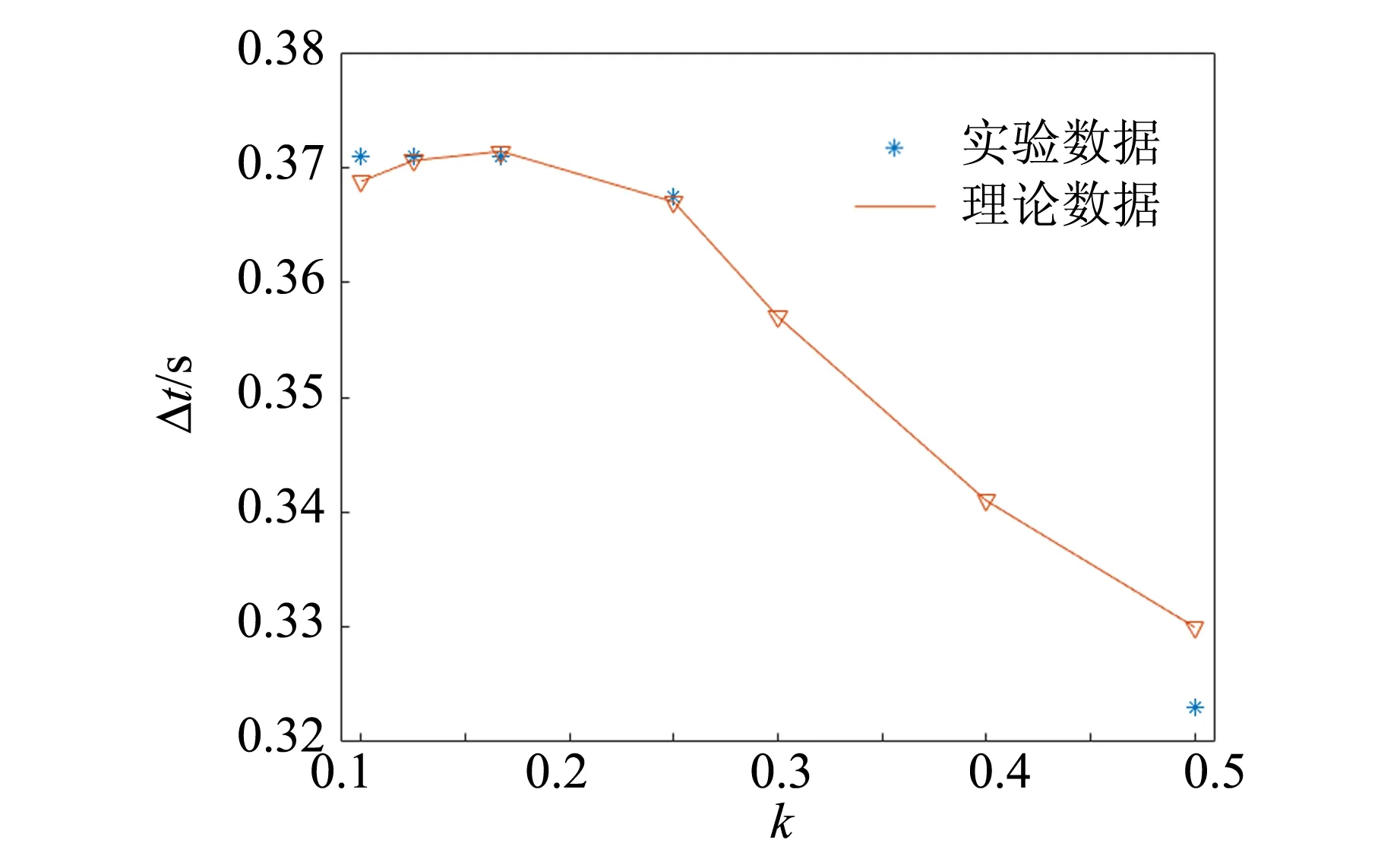
圖16 Δt與k的關系(R=4.85 mm,μ=0.192,r0=0.306 m,β=92.8°)
4 結束語
研究了第32屆IYPT賽題中循環擺現象. 通過建立循環擺運動的方程組,理論模擬了質量比、初始繩長對輕重物體運動的影響,并進行了實驗研究. 結果表明,在輕重物體的質量比k小于0.27~0.43,釋放角度β大于68°~90°(均取決于其他初始條件)時,輕物體可以繞桿運動,并可以阻止重物體下落.

