非對稱軌底坡條件下地鐵車輛動力學分析

溫靜 于浩 陳嶸

（1.西南交通大學高速鐵路線路工程教育部重點實驗室，成都 610031；2.西南交通大學土木工程學院，成都 610031）

鋼軌軌底坡是軌道的重要參數，目前國內外鐵路線路上設置的軌底坡主要有1∕40 和1∕20。由于現場安裝精確性不足、扣件墊板彈性降低、軌道環境變化引起地基沉降量不同、軌道結構永久變形等原因，鋼軌軌底坡往往與設計值存在偏差，兩側鋼軌軌底坡出現非對稱現象［1］。軌底坡存在偏差或設置不當會影響輪軌接觸的幾何和力學特性、車輛動力學性能、輪軌磨耗、滾動接觸疲勞性能，對車輛和軌道產生不同程度的破壞。因此，在對車輛曲線通過性能及車輪減磨措施等的研究中，必須考慮軌底坡的影響。

司道林等［2］通過建立重載貨車模型分析了不同軌底坡條件下的靜態輪軌接觸及車輛的曲線通過性能，發現軌底坡由1∕40 增至1∕20 可提高車輛的曲線通過性能。王寧［3］建立了高速鐵路車-線多體動力學仿真模型，探究車輛通過曲線時鋼軌產生側磨的動力學原因，認為內軌采用1∕20 軌底坡、外軌采用1∕40 軌底坡時外軌磨耗指數及輪對沖角較小。李金城等［4］對3 種踏面車輪在不同車輛動力學模型、不同線路條件下的車輪損傷進行了對比分析，結果表明LM 踏面車輪在1∕20軌底坡下的輪軌接觸關系良好。李霞等［5］利用三維彈性體非赫茲滾動接觸理論分析了軌底坡對LM 和LMA 這2 種型面接觸行為的影響，認為軌底坡過大或過小均會使車輪踏面與鋼軌的接觸面積減小，從而接觸應力增大，輪軌的接觸疲勞加劇；軌底坡的設置對降低輪軌橫向力和沖角、改善輪軌接觸條件、減緩鋼軌疲勞至關重要。金學松［6］對輪軌滾動接觸疲勞破壞的幾種典型現象的起因和發展過程進行了定性分析，認為軌底坡設置不合理是我國鐵路輪軌接觸表面疲勞現象的主要原因之一。既有研究主要側重于左右兩側對稱軌底坡的情況，而針對非對稱軌底坡條件下的研究較少。

地鐵長期處在滿負荷甚至是超負荷的工作狀況會使車輪和鋼軌出現車輪異常磨耗、輪軌滾動接觸疲勞引起裂紋等問題，進行軌道結構參數設計時應做充分的基礎研究，以保證地鐵車輛的安全運行。本文從動力學分析的角度出發，研究非對稱軌底坡對我國目前采用的LM地鐵車輪型面與CHN60鋼軌匹配下的車輛動態響應、輪軌磨耗、滾動接觸疲勞等的影響。

1 輪軌滾動接觸計算模型

1.1 車輛系統動力學模型

鐵道車輛是一個多體系統，車輛本身結構、懸掛系統參數存在非線性特性，輪軌相互作用關系復雜，相鄰結構部件之間存在非線性相互作用力。為簡化計算，本文根據一地鐵車輛計算參數（表1），運用多體系統動力學軟件SIMPACK建立車輛動力學仿真模型。模型包括車輛、軌道和輪軌接觸3 部分。建模時考慮二系橫向減振器、二系垂向減振器及二系橫向止擋的非線性力特性，如圖1所示。

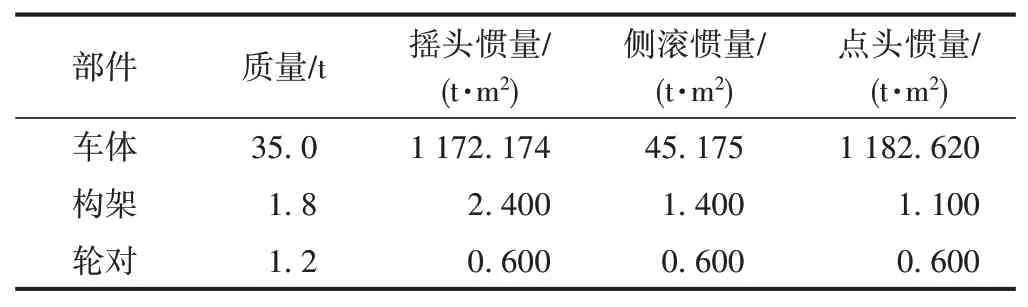
表1 地鐵車輛基本計算參數

圖1 車輛系統動力學模型中的非線性力特性

1.2 輪軌滾動接觸疲勞預測模型

1）輪軌磨耗指數

預測鋼軌表面失效時，用輪軌磨耗指數W（又稱磨耗數）來表示磨耗的強度［7］，計算公式為

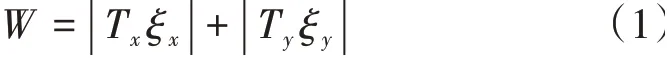
式中：Tx，Ty分別為輪軌縱向、橫向蠕滑力；ξx，ξy分別為輪軌縱向、橫向蠕滑率。

2）表面疲勞指數

采用基于安定圖提出的表面疲勞指數來評價輪軌滾動接觸疲勞特性［8］。表面疲勞指數綜合利用輪軌接觸壓力和切向蠕滑力來評價輪軌的承載能力，可以快速直觀地比較不同運行條件下輪軌的安全性，定性分析輪軌滾動接觸疲勞裂紋發生的機理及可能性。表面疲勞指數FIsurf的計算公式為

式中：μ為牽引系數分別為橢圓接觸斑的短半軸和長半軸；k為材料純剪切屈服強度，取303 MPa；Fz為輪軌法向力。

若算得FIsurf＞0，則認為此時輪軌材料變形將發生棘輪效應，塑性變形會持續累積，直至材料失去韌性而發生疲勞裂紋。

2 結果分析

內軌側軌底坡（以下用RCN表示）取目前常用的1∕40和1∕20，外軌側軌底坡（以下用RCW表示）取1∕20，1∕30，1∕40 和1∕50，利用車輛系統動力學模型，仿真分析不同軌底坡條件下地鐵車輛通過曲線線路時外軌側車輪的動態響應。計算時不考慮軌道不平順的影響，摩擦因數取0.4。曲線線路參數見表2。

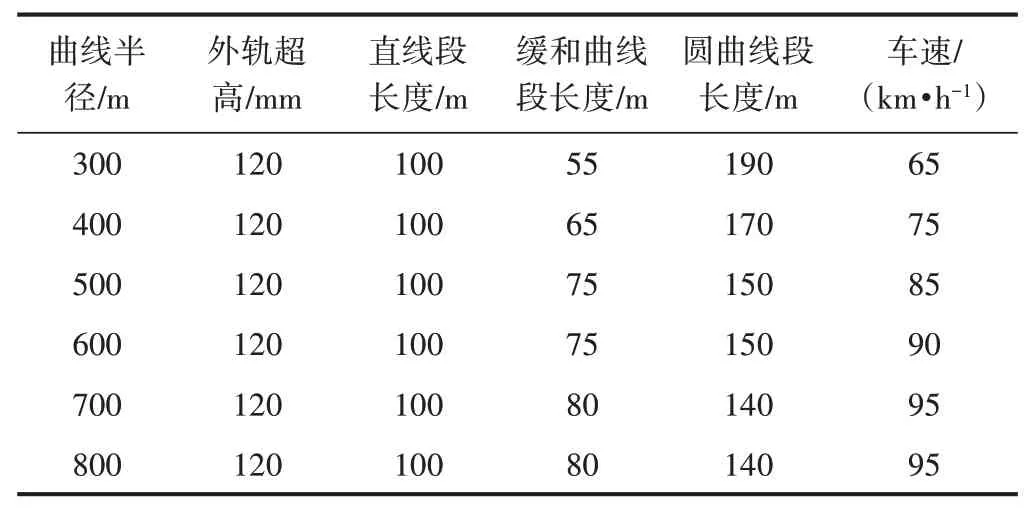
表2 曲線線路參數

2.1 動態響應分析

車輛通過曲線線路時的動態響應評價指標包括輪對橫移量、脫軌系數、減載率以及輪軌縱向蠕滑力、橫向蠕滑力、法向接觸應力等。

輪對橫移量主要與車輛懸掛參數、滾動圓半徑差有關。輪對中心相對于軌道中心偏移較大時易發生輪緣接觸，致使車輪踏面異常磨耗，輪軌接觸關系惡化。脫軌系數和減載率是我國車輛部門評定車輛運行安全性時采用的2項主要指標。不同軌底坡條件下輪對橫移量、脫軌系數、減載率隨曲線半徑的變化情況見圖2。

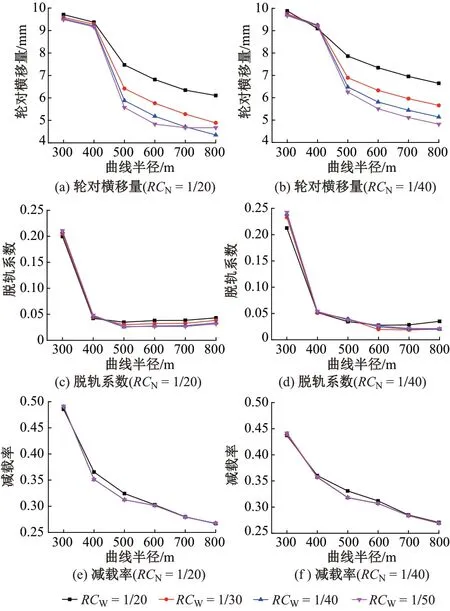
圖2 輪對橫移量、脫軌系數、減載率隨曲線半徑的變化情況

從圖2（a）和圖2（b）可知：曲線半徑為300～400 m時，輪對橫移量較大，為9～10 mm，可能導致輪緣接觸的發生；隨著曲線半徑的增大，輪對橫移量明顯減小；同一曲線半徑下，輪對橫移量隨外軌側軌底坡的減小而減小，但RCN=1∕20、曲線半徑為800 m時，RCW=1∕50的輪對橫移量高于RCW=1∕40。

從圖2（c）和圖2（d）可知：曲線半徑小于500 m時，脫軌系數隨曲線半徑的增大而迅速減小；隨著曲線半徑的增大，脫軌系數的變化趨于平緩；非對稱軌底坡與對稱軌底坡條件下的脫軌系數差異不大。

從圖2（e）和圖2（f）可知：曲線半徑為400～600 m時，RCW為1∕30～1∕50 的減載率相同，且均低于RCW=1∕20，其他曲線半徑下減載率不受軌底坡變化的影響。

我國脫軌系數和減載率安全限定值均為0.8。從圖2 可知，不同軌底坡條件下，曲線半徑為300 m 時脫軌系數和減載率均達到最大值，且均低于0.8。

輪軌蠕滑力直接影響列車的牽引特性，蠕滑力達到輪軌間極限摩擦力時輪軌出現完全滑動。不同軌底坡下輪軌接觸應力隨曲線半徑的變化情況見圖3。

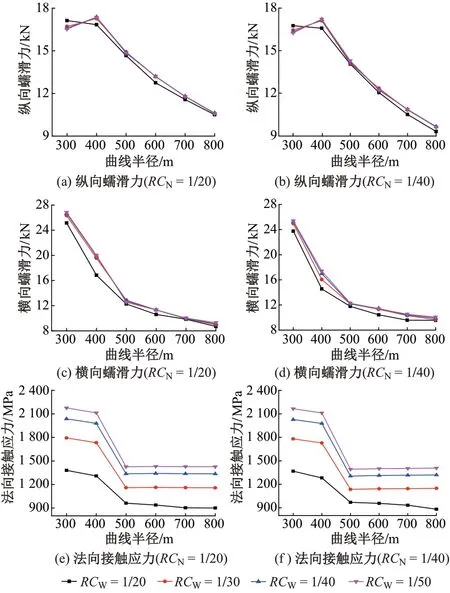
圖3 輪軌接觸應力隨曲線半徑的變化情況

從圖3（a）和圖3（b）可知：曲線半徑為300～400 m時不同軌底坡條件下的縱向蠕滑力均較大，約為16～18 kN；曲線半徑大于400 m 時，不同軌底坡條件下的縱向蠕滑力均隨曲線半徑的增大而明顯減小，且同一曲線半徑下幾乎相等。

從圖3（c）和圖3（d）可知：不同軌底坡條件下的橫向蠕滑力均隨曲線半徑的增大而明顯減小；同一曲線半徑下，RCW<1∕20 時的橫向蠕滑力幾乎相等且均略高于RCW=1∕20。

從圖3（e）和圖3（f）可知：不同軌底坡條件下的法向接觸應力均隨曲線半徑的增大而減小；同一曲線半徑下法向接觸應力隨外軌側軌底坡的減小顯著增加，如曲線半徑為300 m 時，1∕20 對稱軌底坡條件下的法向接觸應力為1 379 MPa，而RCN=1∕20，RCW=1∕50 時法向接觸應力增至2 177 MPa，增大了57.9%，可見法向接觸應力受軌底坡變化影響顯著。

從圖2、圖3 可以看出，RCN=1∕40 條件下各參數隨曲線半徑的變化情況均與RCN=1∕20 相似，說明外軌動態響應主要與外軌側軌底坡的設置有關，受內軌側軌底坡的影響較小。

2.2 輪軌接觸滾動損傷分析

以曲線半徑為300 m 為例，利用輪軌滾動接觸疲勞預測模型，研究車輛通過曲線時非對稱軌底坡對輪軌磨耗及滾動接觸疲勞的影響。

根據式（1）算出不同軌底坡條件下的輪軌磨耗指數W，見圖4。可知：車輛通過曲線線路時不同軌底坡條件下均有W＞100 Nm∕m；輪軌磨耗指數隨外軌側軌底坡變化顯著；對于RCN=1∕20，對稱軌底坡條件下W最大值為134 Nm∕m，RCW=1∕50 時增大至150 Nm∕m；對于RCN=1∕40，對稱軌底坡條件下W最大值為151 Nm∕m，RCW=1∕20時減小至136 Nm∕m。可見，外軌側軌底坡減小會加劇輪軌磨耗。

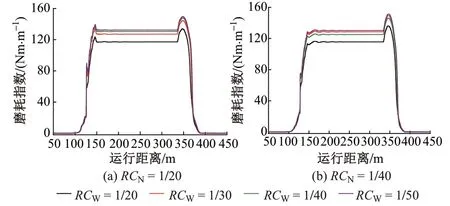
圖4 不同軌底坡條件下的輪軌磨耗指數

表面疲勞指數FIsurf可用來表征產生滾動接觸疲勞的可能性。FIsurf>0 表示有可能產生疲勞損傷。根據式（2）和式（3），算出不同軌底坡條件下的表面疲勞指數，見圖5。可知：車輛通過圓曲線段時不同軌底坡條件下均有FIsurf>0；隨著外軌側軌底坡減小，表面疲勞指數明顯增加；對于RCN=1∕20，對稱軌底坡下FIsurf最大值為0.145，RCW=1∕50 時為0.247，增大了70%；對 于RCN=1∕40，RCW=1∕20 時FIsurf最 大 值為0.132，RCW=1∕50 時為0.245，增大了46%。可見，外軌側軌底坡的減小會惡化輪軌表面疲勞性能。

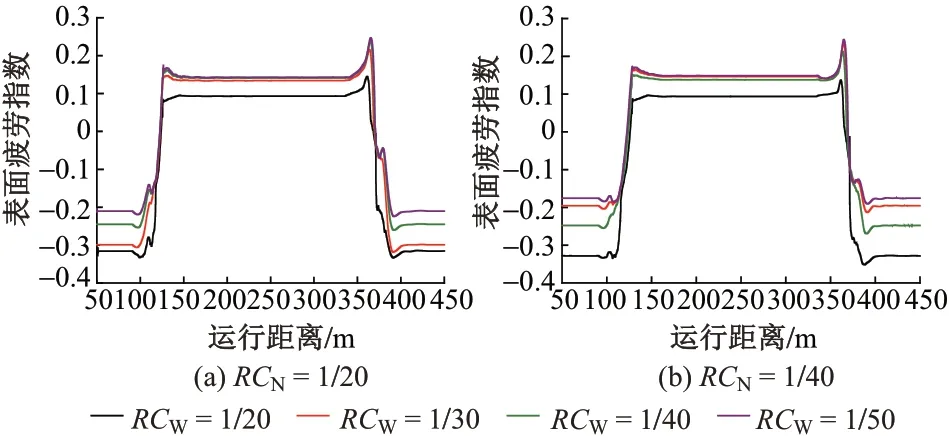
圖5 不同軌底坡條件下的車輪表面疲勞指數

3 結論

1）車輛通過300～400 m 的小曲線半徑時，輪對橫移量較大，易發生輪緣接觸；曲線半徑增大到500 m后，車輛通過曲線時的輪對橫移量明顯減小。脫軌系數和減載率受軌底坡影響較小。

2）輪軌縱向、橫向蠕滑力受軌底坡影響很小；同一曲線半徑下，輪軌法向接觸應力隨外軌側軌底坡的減小而顯著增加。

3）設置非對稱軌底坡時，外軌動態響應主要與外軌側軌底坡有關，受內軌側軌底坡的影響較小。

4）隨著外軌側軌底坡減小，輪軌磨耗指數和表面疲勞指數顯著增大，致使輪軌磨耗加劇，表面疲勞性能惡化。

5）為減緩外軌磨耗及滾動接觸疲勞，建議內軌側軌底坡采用1∕40、外軌側軌底坡采用1∕20。