動態加載方式下防爆墻動力響應分析

趙旭 侯博晗 席聰 譚英華

摘要：為分析防爆墻在不同爆炸載荷下的動力響應和破壞機理，研究波紋板式防爆墻與平板式防爆墻的差異，分別采用三角波加載和基于流固耦合方法的爆炸仿真2種動態加載方式模擬爆炸載荷。分析結果表明：三角波載荷可以較好地模擬爆炸載荷且具有明顯的計算速度優勢。分析得到2種類型防爆墻的P-I曲線，通過對比發現波紋板式防爆墻的抗爆性能優于平板式防爆墻。

關鍵詞：防爆墻;爆炸載荷;三角波;流固耦合;動力響應;P-I曲線

中圖分類號：TP391.99;TU352.13文獻標志碼：B

0 引言

抗爆設計對可能發生爆炸災難風險的建筑具有重要意義。與其他防爆措施相比，防爆墻具有經濟、空間布置靈活、防爆能力強等優點。國內關于防爆墻的研究起步相對較晚，但是近年來涌現大量關于墻體抗爆性能的研究成果。王仲琦等基于多物質流體的歐拉算法，對爆轟產物采用JWL狀態方程，并運用其自行編制的SMMIC通用程序，研究爆炸沖擊下不同防護墻對沖擊波發展過程和擴散規律的影響。吳媛媛等利用LS-DYNA軟件，對近地爆炸下剛性墻繞流現象進行數值模擬，研究超壓時程規律及其影響因素。師吉浩等運用LS-DYNA軟件分析3種波紋板式防爆墻在不同爆炸載荷作用下的動態響應和破壞機理，擬合3種類型波紋板式防爆墻的抗爆評估P-I曲線，為初始抗爆設計提供參考。張雄等研究物質點法模擬爆炸問題，在物質點有限元法和局部多重背景網格算法基礎上開發針對沖擊爆炸問題的三維顯式并行MPM數值仿真軟件MPM3D，為爆炸研究提供工具。

三角波加載和通過建立歐拉區域模型進行流固耦合爆炸模擬分析是研究防爆墻動力性能常用的2種動態加載方式。后者往往計算成本較高，且參數不易修改。本文分析比較2種不同爆炸載荷動態加載方式下防爆墻的中心位移響應，結果表明2種動態加載方式下模擬分析結果吻合較好，驗證三角波動態加載方式的合理性和有效性。三角波加載具有明顯的計算速度優勢，因此本文采用三角波加載方式對比分析波紋板式防爆墻和平板式防爆墻的防爆性能，并借助P-I曲線直觀研究2種防爆墻性能的差異。

1 2種動態加載方式

1.1三角波加載爆炸模擬

依據防爆墻與爆炸源的距離不同，爆炸可分為遠距離爆炸和近距離爆炸。研究爆炸沖擊載荷時，需要將所有的爆炸物換算為TNT炸藥，距離也要用換算距離替代。由于爆炸過程環境變化的復雜性，沖擊波各參數很難通過理論分析獲得。本文選擇HENRYCHL提出的無限域空氣中炸藥爆炸峰值壓力經驗計算公式（式（1）和（2））確定爆炸沖擊波的人射超壓峰值平_S0及其對應時間t₀。

1.2 基于流固耦合方法的爆炸模擬

任意拉格朗日-歐拉（arbitrary Lagrangian-Eulerian，ALE）算法是NOH在研究有限差分法時提出的，后來被HUERTA等引人有限元法中，其基本思想是計算網絡既不固定也不依附于流體質點，而是可以相對于坐標系任意運動。

這種方法最先出現在數值模擬流體動力學問題的有限差分法中，其擁有拉格朗日和歐拉2種算法的優點：首先，在結構邊界運動問題的處理上繼承拉格朗日算法的優勢，能夠有效追蹤物質結構邊界的運動;其次，在內部網格劃分上吸收歐拉算法的優勢，使其內部網格單元獨立于物質實體而存在。但是，與歐拉算法網格不完全相同，ALE算法網格可以根據定義的參數在求解過程中適當調整位置，使得網格不會出現嚴重畸變，這種方法在進行爆炸模擬分析時非常有利。

基于JWL狀態方程理論，采用通用有限元軟件LS-DYNA中的。Me_Multi_Material_Group多物質單元實現使用流固耦合算法模擬爆炸的過程：對炸藥和空氣材料采用歐拉算法，其他結構采用格朗日算法，然后通過流固耦合的方式模擬兩者之間的相互作用。

2 計算模型

2.1 平板式防爆墻幾何模型

采用方形平鋼板作為防爆墻，鋼板尺寸為8.80m×8.80m，厚度為0.02m，分別采用2種動態加載方式模擬其承受的爆炸載荷。鋼板單元類型選擇SHELLl63，炸藥單元和空氣單元都用三維顯式結構實體單元SOLIDl64。炸藥尺寸為0.50m×0.50m×0.50m的立方體，空氣為9.00m×9.00m×13.50m的立方體，防爆墻與爆炸源的距離為10.00m，防爆墻四周為固支約束。防爆墻流固耦合計算模型見圖2。

2.2 平板式防爆墻材料的本構模型

在計算模型中，鋼采用LS-DYNA中的*Mat_Plastic_Kinematic材料模型模擬，該材料模型可描述各種各向同性硬化和隨動硬化塑性模型，同時還可以考慮應變率和時效的影響。通過在0（僅隨動硬化）和l（僅各向同性硬化）之間調整硬化參數盧實現隨動或各向同性硬化。鋼板采用考慮應變率效應的Cowper-Symonds本構模型，本構方程為

2.3 炸藥和空氣材料參數及其狀態方程

在數值模擬中，目前廣泛使用的爆轟產物狀態方程主要有BKW、LJD、JCZ和JWL等，此處TNT炸藥的材料模型采用JWL狀態方程描述，即式中：P為爆轟產物壓力;V為相對體積;E為TNT炸藥單位質量的內能;A、B、R₁和R₂為材料常數。TNT炸藥JWL狀態方程相關參數見表2，其中v為TNT炸藥的爆速。

采用理想氣體狀態方程描述空氣，其壓力P和內能e₀的關系為

P=（r-1）ρ₀e₀（8）

式中：ρ₀為空氣密度;e₀為單位質量氣體的內能;r為材料常數。空氣相關參數見表3。

2.4 單元收斂性檢驗

先選取40000個單元，然后以40000個單元為公差等差式增加單元數量，共采用6組單元進行模型網格依賴性分析。防爆墻中心最大位移隨單元數量的變化規律見圖3。

由圖3可知，當單元數量超過120000個之后，單元數量對計算結果影響很小。因此，確定計算網格單元尺寸為0.20m×0.20m×0.20m，防爆墻單元總數為7744個，空氣和炸藥的單元總數為150212個，模型總計157956個單元。

3 計算結果分析

3.1 爆炸沖擊波分布變化規律

采用歐拉單元建立炸藥和空氣模型，采用拉格朗日單元建立防爆墻模型，進行流固耦合計算，得到不同時刻空氣和防爆墻的壓力云圖，分別見圖4和5。由此可觀察爆炸沖擊波在空氣中的傳播：在9ms時沖擊波完全到達防爆墻，此時沖擊波波面近似為平面，且除防爆墻中心部分外其他各處壓力基本相等。

3.2 2種動態加載方式下防爆墻的動力響應對比

在沖擊載荷下，防爆墻最大位移發生在鋼板中心位置，因此以中心點的最大位移為研究對象，其時程曲線見圖6。

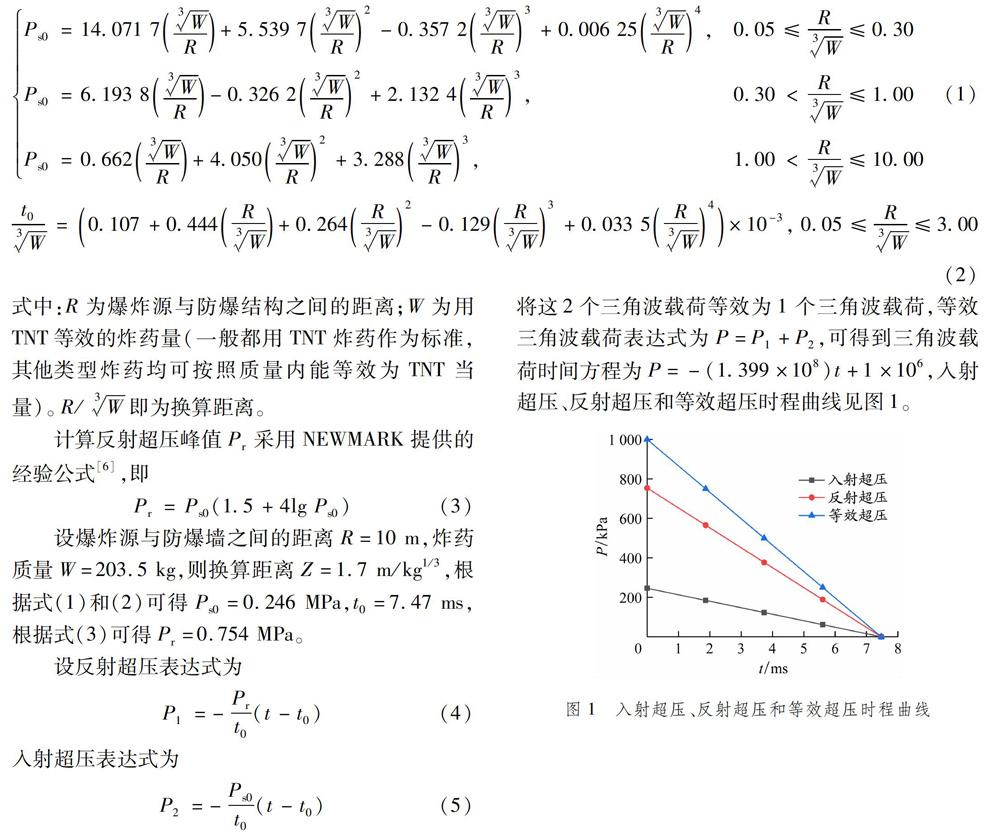
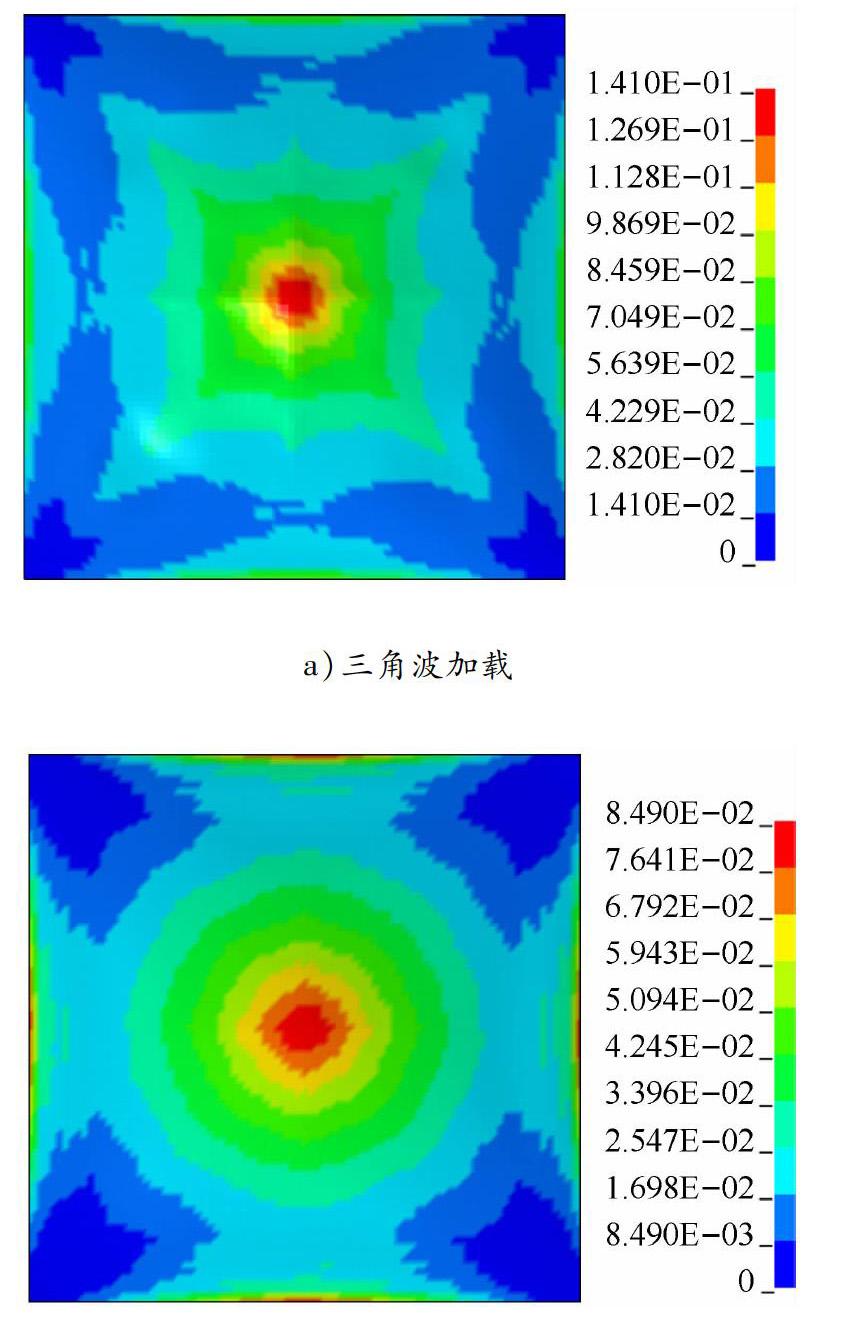
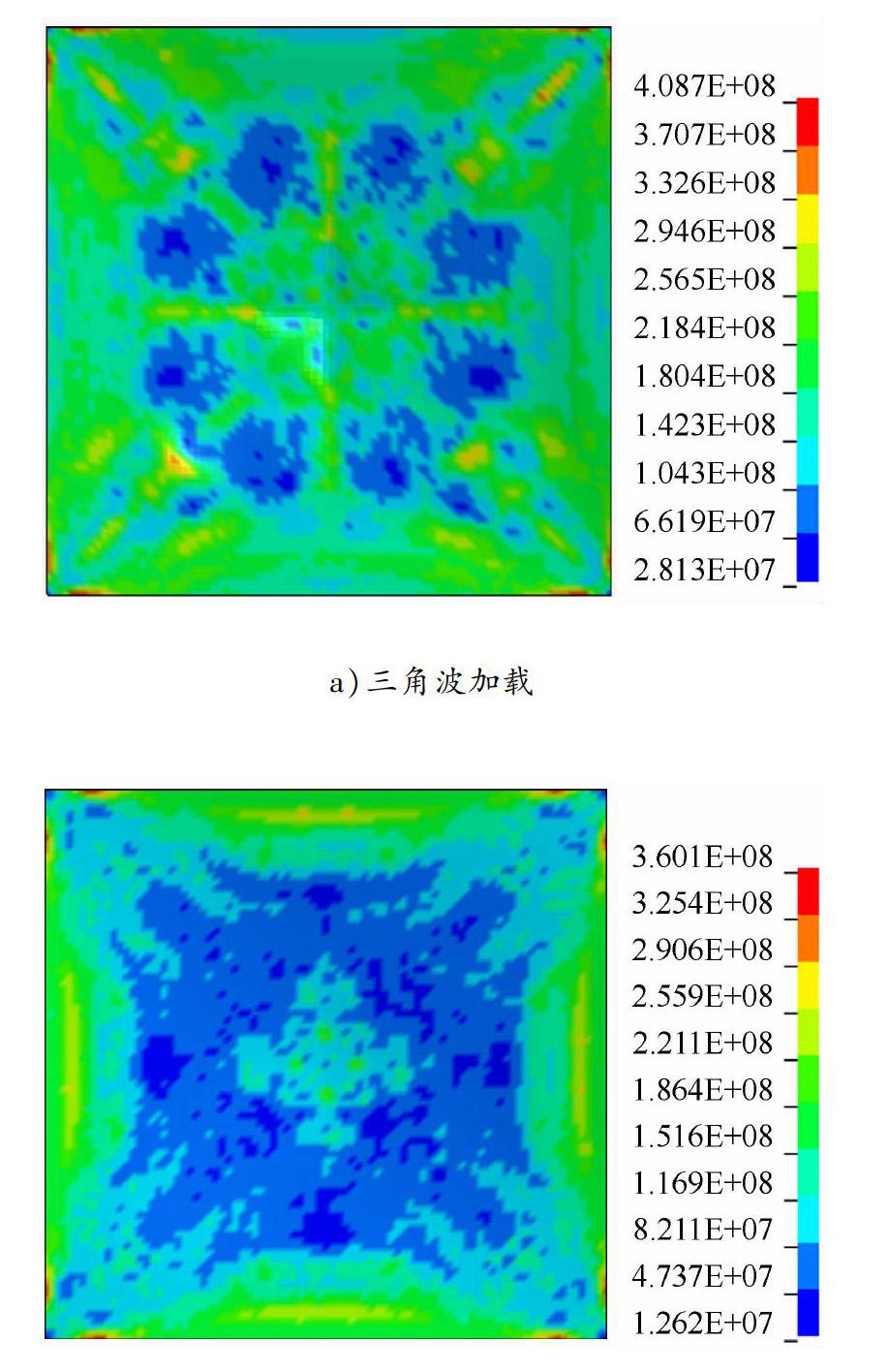
由圖6可以看出，在三角波動態加載方式下，防爆墻的最大塑性位移較大，與流固耦合計算載荷位移的差值約為流固耦合計算載荷位移結果的22%。2種動態加載方式下防爆墻等效應變云圖和VONMises應力云圖分別見圖7和8。由此可以看出：在2種動態加載方式下，防爆墻等效應力和等效應變云圖均大致相同，其應力、應變分布規律基本一致;三角波載荷下的最大等效塑性應變較大，兩者之間的差值為流固耦合計算載荷下應變結果的60%;三角波載荷下最大VON Mises應力較大，兩者之間的差值為流固耦合計算載荷下應力結果的13%。

綜上所述，三角波載荷可以較好地模擬爆炸沖擊載荷，且具有明顯的計算速度優勢，因此研究簡單計算模型采用三角波載荷可節約計算成本。

4 三角波動態加載方式下波紋板式防爆墻與平板式防爆墻動力響應對比

4.1波紋板式防爆墻模型

取波紋板式防爆墻與平板式防爆墻尺寸相同，均為8.80m×8.80m，其材料模型也與平板式防爆墻相同，波紋板式防爆墻有限元模型見圖9。波紋板式防爆墻四周仍采用固支約束，網格尺寸為0.10m×0.10m。為比較2種防爆墻的抗爆性能，設2種防爆墻用鋼量相同，因此波紋板式防爆墻厚度取6.0mm，平板式防爆墻厚度為7.4mm，借助P-I曲線對比分析兩者的防爆性能。

4.2 P-I曲線

依據文獻[11]繪制P-I曲線，采用三角波加載模擬爆炸載荷。繪制P-I曲線首先需要確定失效準則。下面是2種常用的失效準則。

4.2.1 以失效應變定義失效準則

平板式和波紋板式防爆墻等效應變云圖分別見圖10和11。計算分析結果表明：平板式防爆墻的中心位置率先達到失效應變;波紋板式防爆墻四周的約束邊界處率先達到失效應變。

以失效應變定義P-I曲線的失效準則時，波紋板式防爆墻的P-I曲線形狀不理想，其原因是難以得到波紋板式防爆墻約束邊界處單元的真實應變，這是約束引起的應力奇異現象導致的。若以達到失效應變作為失效準則，而波紋板最大應變出現在被約束波紋板的邊界處，則無法獲得有效應變值，說明該失效準則不適用于本文方法。

4.2.2 以最大塑性位移定義失效準則

一般將防爆墻的極限狀態作為防爆墻抗爆設計的依據，因為爆炸事故是低概率事件，所以建筑結構的抗爆設計通常不夠充分，其應變、應力和撓曲位移極易超越彈性極限，因此應以極限狀態考慮爆炸事故設計狀況。在爆炸載荷作用下，防爆墻的典型屈服極限值為墻長l的1/40-1/25，這里選取1/25，將最大塑性位移達到1/25=352mm定義為波紋板式防爆墻的失效準則。

波紋板式防爆墻與平板式防爆墻的最大塑性位移均出現在防爆墻中心位置。采用最大塑性位移失效準則繪制2種防爆墻的P-I曲線，見圖12。

由圖12可知，平板式防爆墻沖量的漸近線在波紋板式防爆墻沖量漸近線的左側，兩者的準靜態漸近線基本一致;與平板式防爆墻相比，波紋板式防爆墻的動態加載區段和沖量加載區段所對應的安全區域均較大，準靜態加載區段對應的安全區域基本相同。綜合分析，波紋板式防爆墻的抗爆性能優于平板式防爆墻。同時，波紋板式防爆墻邊緣和中間部分的應變一直較大，若將這2處區域予以加強，可更好地增強波紋板式防爆墻的抗爆性能。

5 結論

采用通用有限元軟件LS-DYNA對2種動態加載方式下防爆墻的動力響應進行分析，結論如下。

（1）三角波動態加載方式的計算結果與基于流固耦合方法加載的仿真分析結果吻合較好，采用三角波動態加載方式模擬爆炸沖擊載荷具有明顯的計算速度優勢，因此研究簡單計算模型時采用三角波載荷可節約計算成本。

（2）當以最大塑性位移作為失效準則時，與平板式防爆墻相比，波紋板式防爆墻動態加載區段和沖量加載區段所對應的安全區域均較大，準靜態加載區段對應的安全區域基本相同。綜合分析，波紋板式防爆墻的抗爆性能優于平板式防爆墻。

（3）對于波紋板式防爆墻，宜對其邊緣和中間部分進行加厚處理，進而優化波紋板式防爆墻的抗爆性能。