利用Excel進行流網的簡單繪制

摘 要:滲流場的流網圖一般由實驗得出,利用excel的迭代功能可以簡化流網的繪制過程,將Excel迭代產生的數據導入matlab可以得出質量較好的流網圖。
關鍵詞:流網;Excel;matlab;迭代
1.原理介紹
穩定的滲流場中,一組流線和等勢線組成的網格稱為流網圖,利用流網可以確定滲流的諸多要素。對二維滲流場的拉普拉斯方程進行五點差分,可以得出滲流場流函數及勢函數的迭代公式,作為常見數學分析工具的Excel,具有很強的數值處理能力。本文利用Excel的迭代功能求解二位滲流的拉普拉斯方程,可以得出滲流場的流網圖。
2.勢函數值求解
我們可以假設上游水位15m,下游水位5m,并給定滲流區域的初始邊界為:長250m,寬100m,邊界輪廓線看作流線,每天與其相交的勢函數線要與其垂直。將此區域離散化為251×101個方格。
2.1設定邊界條件
由于邊界很大,需要的單元格數目很多,計算時我們選擇了Excel2010版本。
離散后的每個方格為Excel的一個單元格,共有251列、101行,閘基上游邊界區域我們將其賦值為15,閘基下游邊界我們將其賦值為5。滲流區域的外邊界我們將其賦值為其內側兩行或兩列的均值,其中,閘基所在位置無水流通過,將其賦值為0。如圖1所示。
2.2迭代功能的實現
內部網格的所有求解表達式均為周圍網格值的均值,比如B3=(B2+B4+A3+C3)/4。在Excel窗口中點擊“文件”? ? “選項”? ? “公式”,設定迭代次數和迭代精度,為保證生成滲流網足夠光滑,我們設置迭代30000次,精度0.00001。
3流函數值求解
流函數的求解相對簡單,可將除上游邊界以外的外邊界網格值設置為15,第一行的網格值設置為齊下兩行的網格值的平均值,如B2=(B3+B4)/2。其余單元格的值設置為周圍單元格的值的均值。閘基所在位置的流函數值同樣設置為0。
4利用matlab繪制流網圖
將勢函數及流函數迭代產生的值導入matlab中,編寫一個簡單的程序,命令如下:
clear all
l=xlsread('Laplace.xlsx',1,'A1:IQ101');%讀取表一
s=xlsread('Laplace.xlsx',2,'A1:IQ101');%讀取表二
[x,y]=meshgrid(1:251,1:101);%x,y為101行,251列的矩陣
%
figure%呼出圖片
[C1,h1]=contour(x-1,-y+1,s,quantile(s(:),25),'r','showtext','off');%由于表格從坐標(1,1)開始讀取,故取x-1,y-1,且需要縱坐標取負數
h1.LineColor='r';
hold on
[C2,h2]=contour(x-1,-y+1,t,'LevelList',[2.1 4.1 6.1 8.1 9.5 10.5 11.5 12.5 13.5 14.5]);%繪制兩種滲流線
h2.LineColor='b';
x=[0 75 75 80 85 165 170 175 175 250 250 0 0];
y=[0 0 -10 -10 -5 -5 -10 -10 0 0 -100 -100 0];
plot(x,y,'r-');%描出邊界
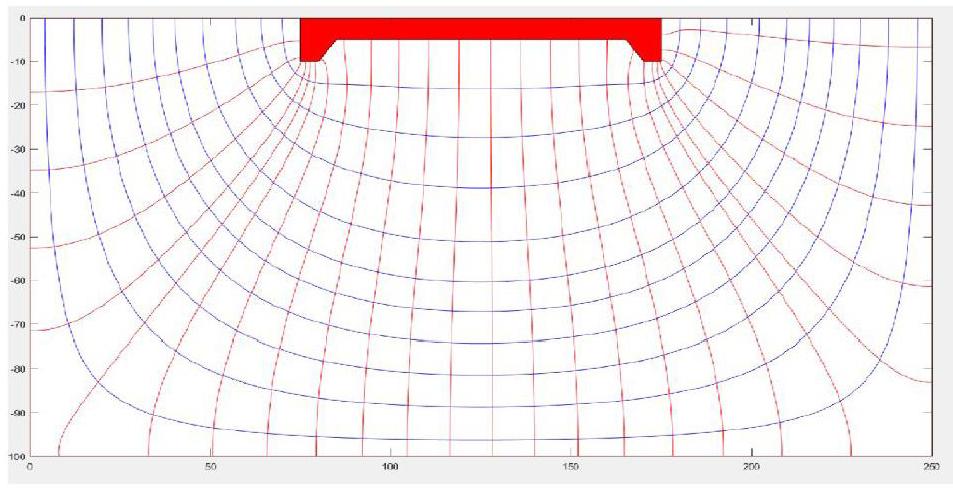
運行程序后,得到了一張流網圖,如下圖所示。
該流網圖與實際效果擬合的很好。
5.總結
本文是作者畢業設計中滲流場網格劃分的一部分,避免了繁雜的水電比擬法,希望能夠對同類設計提供借鑒。
參考文獻:
[1]趙智濤.復雜邊界條件下流網的簡易繪制方法.
[2]賈新民、嚴文.有限差分法求解拉普拉斯方程.
作者簡介:
陳丙舒(1998.09-)男,漢族,黑龍江省齊齊哈爾市,本科生,研究方向:水利水電工程

