基于DTCWT域統(tǒng)計特征融合的紋理圖像檢索

曲懷敬，王恒斌，徐佳，王紀委，魏亞南

（山東建筑大學 信息與電氣工程學院，山東 濟南250101）

0 引言

隨著多媒體數(shù)據(jù)庫和計算機網(wǎng)絡的廣泛應用，其包含的海量有用視覺信息需要采用基于內(nèi)容的圖像檢索CBIR（Content-Based Image Retrieval）技術進行自動、快速而準確地查訪［1］。紋理是自然圖像的一種便于區(qū)分的基本視覺特征，也是呈現(xiàn)在其中的一種基本形態(tài)［2］。紋理圖像代表了一大類自然圖像，而紋理圖像檢索在圖像處理、模式識別、計算機視覺、遙感監(jiān)測、公安刑偵和醫(yī)學診斷等領域中得到了廣泛的應用［1，3－4］。由于紋理圖像可以視為一個隨機過程的實現(xiàn)，因此目前基于統(tǒng)計建模的紋理圖像檢索已成為CBIR領域的前沿研究內(nèi)容。

通常，優(yōu)良的基于變換域統(tǒng)計建模的紋理圖像檢索系統(tǒng)需要較低復雜度的多尺度變換、有效的分布參數(shù)估計方法和只依賴于統(tǒng)計參數(shù)的相似性測度。近十幾年來，圍繞這個要求，眾多學者提出了許多基于變換域統(tǒng)計建模的紋理圖像檢索方法。Do等［5］在離散小波變換域?qū)⒓y理圖像高頻子帶建模為廣義高斯分布GGD（Generalized Gaussian Distribution）；Kwitt等［6］在雙樹復小波變換域?qū)⒓y理圖像高頻子帶幅值系數(shù)建模為Gamma分布或Weibull分布；Yang等［7］基于非下采樣Contourlet變換將方向子帶系數(shù)建模為Weibull分布；楊娟等［8］在雙樹復小波變換域?qū)⒓毠?jié)子帶系數(shù)建模為雙廣義高斯分布；Vo等［9］將均勻離散Curvelet復變換域的實部和虛部子帶建模為GGD分布、相對相位子帶建模為Vonn分布；李朝榮等［10］在離散小波變換域，將細節(jié)子帶系數(shù)建模為高斯Copula聯(lián)合統(tǒng)計分布，在上述方法中，相似性測度均采用K-L（Kullback-Leibler）距離。

紋理可以視為由位置、尺度和方向上覆蓋范圍廣泛的多重分量疊加而成。如上所述，大多數(shù)紋理圖像表示的方法采用的是單一類特征，不能充分地反映局部紋理的細節(jié)結構，從而丟失了刻畫紋理圖像的許多重要信息。為此，需要采用多類特征互補融合的方法來解決這一問題。近年來，多特征融合與對應的相似性測度加權組合是廣泛采用的、有效的紋理圖像檢索方法［11］，在多尺度變換域，將各子帶系數(shù)的統(tǒng)計特征進行互補融合可以有效地提高紋理圖像檢索的性能。殷明等［12］基于非下采樣剪切波變換域提出一種紋理圖像檢索方法，其中特征向量采用廣義高斯分布參數(shù)特征和RI－LPQ特征融合，相似性測度采用K－L距離和歐氏距離的加權平均。Ves等［13］在小波框架域?qū)⒓y理圖像高頻水平和垂直子帶組合構成復值子帶，并將其幅值系數(shù)建模為廣義Gamma分布，相位系數(shù)建模為廣義von Mises分布，相似性測度基于這兩種分布參數(shù)特征融合選用最優(yōu)加權的對稱K－L距離。Qu等［14］在金字塔雙樹方向濾波器組復變換域，將高通子帶系數(shù)建模為廣義高斯分布，復值方向帶通子帶的幅值系數(shù)建模為Gamma分布并融合了相對相位的能量特征，相似性測度選用閉式K－L距離和歐氏距離的加權平均。這些方法大多利用了高頻復值子帶的幅值信息和相位信息，但并未對低頻概貌子帶的信息進行利用。

在基于金字塔雙樹方向濾波器組復變換域?qū)y理圖像檢索方面的探索研究工作中，提出了一種基于混合建模的紋理圖像檢索方法，將高頻子帶系數(shù)建模為廣義高斯分布、幅值帶通子帶系數(shù)建模為Weibull分布，但是沒有利用概貌子帶和相位子帶系數(shù)信息［14－15］。為充分利用復變換域各子帶系數(shù)，特別是相位子帶系數(shù)的統(tǒng)計特征，同時考慮到金字塔雙樹方向濾波器組復變換域存在相位子帶信息刻畫不足的問題，文章提出一種在雙樹復小波變換DTCWT（Dual-Tree Complex Wavelet Transform）域融合低頻概貌子帶和高頻復值細節(jié)子帶統(tǒng)計分布特征的紋理圖像檢索新方法。其中，低頻子帶采用變換系數(shù)的能量特征和歸一化歐氏距離；高頻幅值子帶系數(shù)采用Weibull分布參數(shù)特征，而高頻相對相位子帶系數(shù)采用wrapped Cauchy分布參數(shù)特征，二者的相似性測度都采用K－L距離。將這些統(tǒng)計特征進行融合，并對相應的相似性測度進行最優(yōu)加權平均求和。通過對VisTex紋理圖像庫進行檢索實驗，以驗證新方法能否有效地提高檢索性能。

1 雙樹復小波變換域中的統(tǒng)計特征提取

DTCWT根據(jù)樹形結構，采用低通和高通濾波器組，分別同時進行實部和虛部的多尺度子帶分解。最終在每尺度下，得到1個組合的低頻概貌子帶，以及6個不同方向（±15°、±45°、±75°）的高頻復值子帶。相應地，可得到每尺度下6個實部高頻細節(jié)子帶和6個虛部高頻細節(jié)子帶。

1.1 低頻子帶系數(shù)的能量特征提取

在一幅紋理圖像中，紋理的分布與灰度值的變化息息相關。灰度值變化的程度越大，在紋理中體現(xiàn)的信息就越豐富，而這種變化在變換域中就體現(xiàn)在每個子帶的能量分布上。因此，紋理圖像的子帶能量可以表征其紋理信息。

在雙樹復小波變換域分別提取紋理圖像1～3層的概貌子帶系數(shù)的分布能量作為特征。能量特征分別由式（1）和（2）［5］表示為

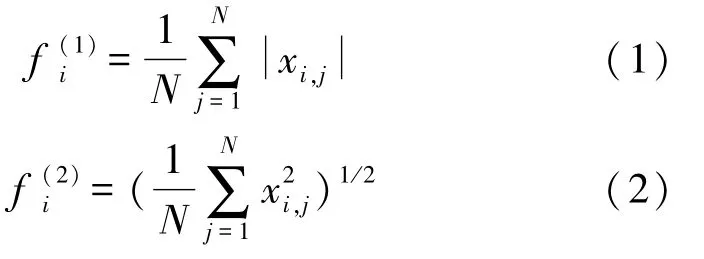
式中：N為概貌子帶系數(shù)的總量；xi，j為第i層概貌子帶的第j個變換系數(shù)。

1.2 幅值子帶系數(shù)的統(tǒng)計特征提取

在DTCWT變換域，對于高頻幅值子帶系數(shù)，根據(jù)其直方圖的包絡形狀，可選用Weibull分布模型進行描述。其概率密度函數(shù)p（x；β，λ）由式（3）［6］表示為

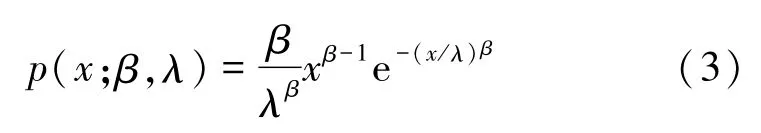
式中：x為幅值隨機變量，0＜x＜∞；β為形狀參數(shù)，β＞0；λ為尺度參數(shù)，λ＞0。

Weibull分布參數(shù)的估計通常采用最大似然的方法。給定 Weibull分布隨機樣本集X ＝{x1，x2，…，xΝ} ，并假定樣本是獨立同分布的，則定義似然函數(shù)L由式（4）表示為

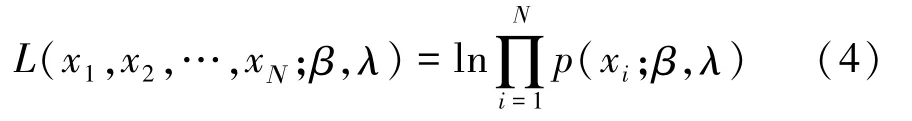
根據(jù)最大似然估計方法，則尺度參數(shù)λ與超越方程分別由式（5）和（6）表示為

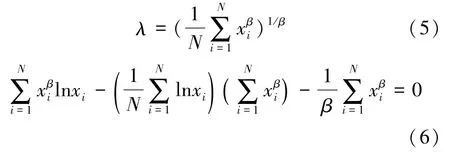
式（6）可通過Newton-Raphson迭代方法進行數(shù)值求解［6，15］，求出形狀參數(shù)β，則由式（5）可確定尺度參數(shù)λ。

只有當所選的初值和真實值相接近時，Newton-Raphson迭代方法估計的結果才準確。因此，采用變步長迭代算法估計形狀參數(shù)β［15］，β的初值由方差系數(shù)根據(jù)查詢表確定。方差系數(shù)KC由式（7）表示為

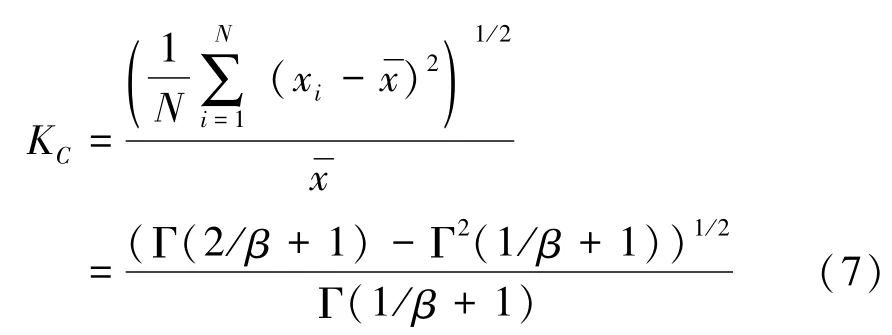
式中：為 Weibull隨機分布樣本集X ＝{x1，x2，…，xN} 的均值Γ為Gamma函數(shù)。

1.3 相對相位子帶系數(shù)的統(tǒng)計特征提取

紋理圖像經(jīng)過雙樹復小波變換后，由各尺度下的復值子帶系數(shù)可以得到對應的相位子帶系數(shù)。通常，相位子帶系數(shù)直方圖的分布是均勻的［16］，如圖1所示。然而，這種均勻分布的相位不能產(chǎn)生區(qū)分紋理圖像的任何信息，為此需要采用相對相位。在相位子帶的空間位置（i，j）處，定義相對相位θ（i，j）由式（8）表示為

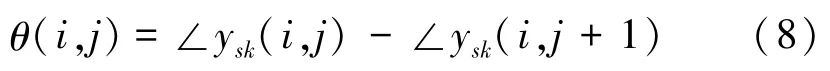
式中：∠為相位；ysk（i，j）為在s尺度、k方向子帶下，位置為（i，j）處的復值系數(shù)。

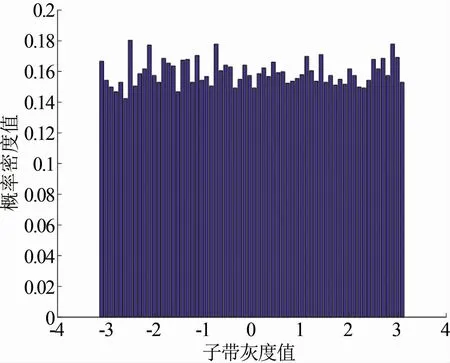
圖1 相位子帶系數(shù)分布直方圖

相對相位子帶系數(shù)分布直方圖如圖2所示。相對相位系數(shù)的統(tǒng)計分布可以有效地刻畫紋理圖像的區(qū)分信息。通常，相對相位系數(shù)可通過wrapped Cauchy分布進行有效地建模。wrapped Cauchy分布的概率密度函數(shù)p（θ；ρ，μ）由式（9）［16］表示為

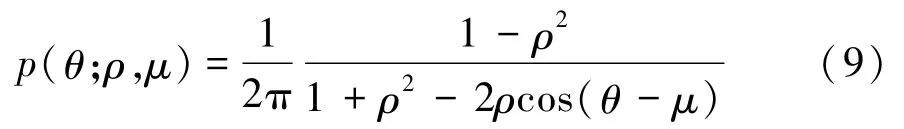
式中：θ為相對相位系數(shù)，θ∈［－π，π］；μ為位置參數(shù)，μ∈［－π，π］；ρ為尺度參數(shù)，ρ∈［0，1］，其值越大，對應的概率密度曲線就越尖銳。

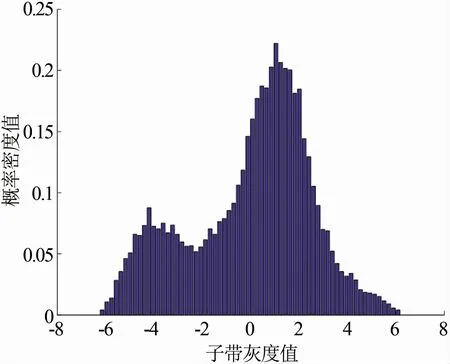
圖2 相對相位子帶系數(shù)分布直方圖

給定一組獨立的、符合wrapped Cauchy概率密度p（θ；ρ，μ）分布的觀測數(shù)據(jù)集合｛θ1，θ2，···，θN｝，根據(jù)最大似然方法，采用迭代算法可估計位置參數(shù)和尺度參數(shù)［16］。其中，迭代方程分別由式（10）～（12）表示為

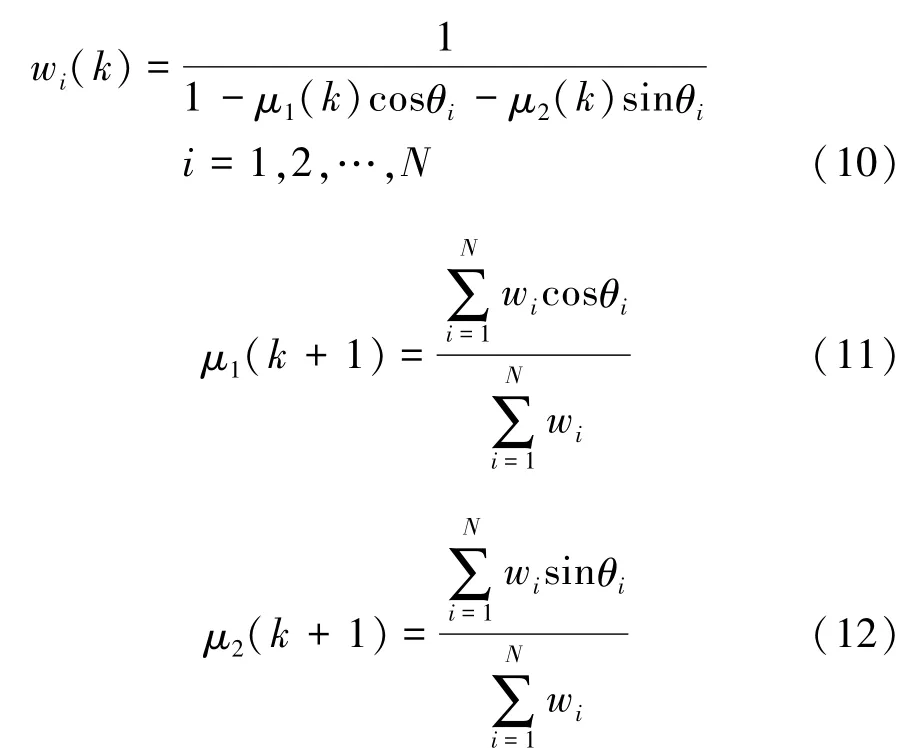
式中：k為迭代指針。

當?shù)惴ㄊ諗亢螅謩e得到估計值μ1和μ2，則位置參數(shù)μ和尺度參數(shù)ρ的估計值分別由式（13）和（14）表示為

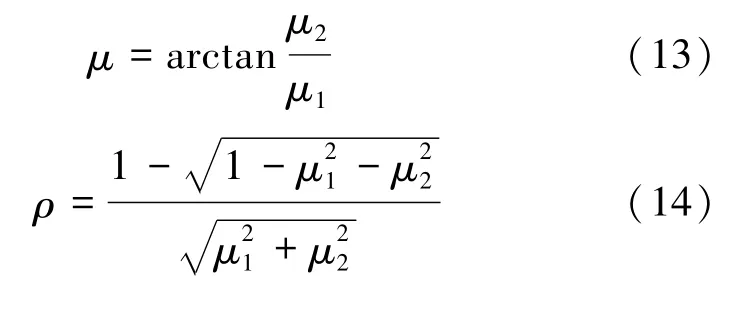
2 基于統(tǒng)計特征融合的紋理圖像檢索方法

2.1 紋理數(shù)據(jù)庫的建立

為了便于檢索性能的比較，所采用的實驗圖像取自廣泛使用的VisTex數(shù)據(jù)庫［5］，包括40類大小為512 pixel×512 pixel的彩色紋理圖像。紋理數(shù)據(jù)庫建立步驟為：（1）將彩色紋理圖像變換為灰度圖像；（2）將每一個圖像不重疊地分割為16個128 pixel×128 pixel的灰度子圖像。最終建立了一個具有40類、每類16個子圖像、總數(shù)為640個的灰度紋理圖像標準實驗數(shù)據(jù)庫。為了減少同類子圖像間灰度值的相關性和保持檢索過程的公平性，將所有子類圖像分別歸一化為零均值和單位標準差。

式中：p（x；β1，λ1）和q（x；β2，λ2）為數(shù)據(jù)庫備選圖像和查詢圖像的Weibull概率密度函數(shù)；γ為歐拉常數(shù)。

對應于相對相位特征，由于wrapped Cauchy分布不存在一個閉式形式的K－L距離，因此相似性測度Dph可根據(jù)K－L距離定義，通過數(shù)值分析的方法

2.2 檢索過程與評價

檢索過程是在未標記的紋理圖像庫中搜索和某一個查詢圖像最相似的若干同類圖像。通常，采用平均檢索率來定量評價檢索系統(tǒng)的性能。在典型的檢索實驗中，查詢圖像選為數(shù)量為Nt的紋理圖像庫中的任一圖像。對于每個查詢圖像，檢索得到的所有正確圖像是同類的其他Nr個圖像。而對于第i個查詢圖像，假定在檢索得到的前M個最相似圖像（不包括查詢圖像本身）中所包含同類圖像的個數(shù)為ni（M），則平均檢索率Ra由式（15）表示為

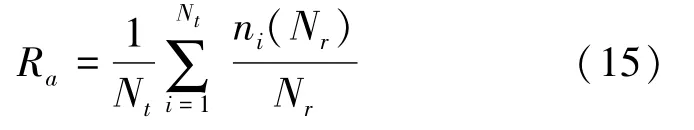
在紋理圖像檢索實驗中，數(shù)據(jù)庫圖像的個數(shù)Nt為640，而與每個查詢圖像同類的其他備選圖像的個數(shù)Nr為15。

2.3 紋理圖像統(tǒng)計特征的計算

獲取紋理圖像統(tǒng)計特征的步驟是：（1）計算紋理圖像經(jīng)雙樹復小波分解后產(chǎn)生的低頻子帶的能量，并作為能量特征；（2）對小波分解后得到的高頻子帶幅值系數(shù)進行Weibull建模，模型的兩個分布參數(shù)作為幅值特征；（3）將高頻子帶相對相位系數(shù)建模為wrapped Cauchy分布，模型的兩個分布參數(shù)作為相位特征。對于每一分解層，能量特征數(shù)為1×2＝2，幅值特征數(shù)為1×6×2＝12，相位特征數(shù)為1×6×2＝12。

2.4 相似性測度的計算

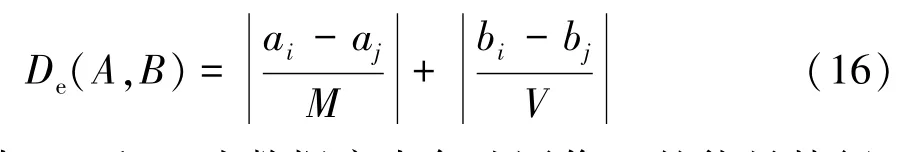
對應于能量特征，選用歸一化歐式距離De作為相似性測度，其定義由式（16）表示為式中：ai和bi為數(shù)據(jù)庫中備選圖像A的能量特征；aj和bj為查詢圖像B的能量特征；M和V分別為整個數(shù)據(jù)庫的能量特征

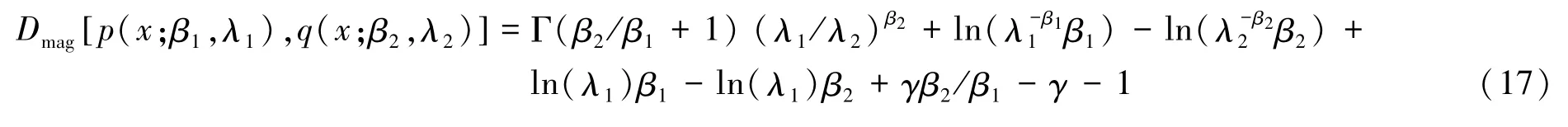
估算，由式（18）表示為

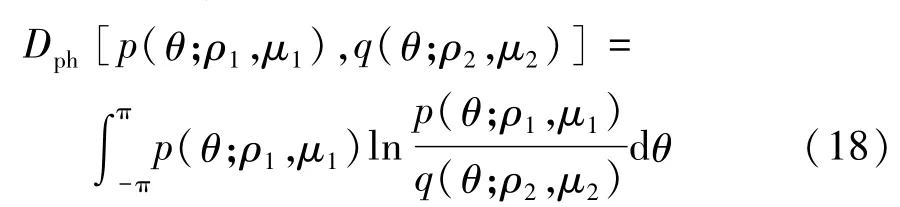
式中：p（θ；ρ1，μ1）和q（θ；ρ2，μ2）分別為數(shù)據(jù)庫備選圖像和查詢圖像的wrapped Cauchy概率密度函數(shù)。

采用的總相似性測度D由式（19）表示為

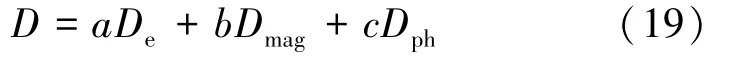
式中：a＋b＋c＝1，且a、b、c的取值范圍為［0，1］。

利用提出的檢索方法，通過Matlab仿真，遍歷整個a和b的取值范圍，取值步長為0.05；并根據(jù)最優(yōu)平均檢索率，選擇a＝0.25、b＝0.35和c＝0.4。

3 紋理圖像檢索實驗結果與分析

3.1 幅值子帶系數(shù)的統(tǒng)計模型選擇

隨機選用VisTex數(shù)據(jù)庫［5］中的Fabric.0009和Food.0005作為典型的實驗圖像，如圖3所示，對其進行3層DTCWT變換。為了比較，針對第1層的－15°高頻復值子帶的幅值系數(shù)分別進行Weibull分布、Gamma分布［6］和GGD分布［5］建模以及相應的直方圖擬合。Fabric.0009、Food.0005圖像的實驗結果分別如圖4（a）～（c）、（d）～（f）所示，各分布圖下括號里的數(shù)值分別為尺度參數(shù)、形狀參數(shù)和熵差率。其中，熵差率（ΔH／H）是用來衡量概率分布擬合程度的客觀參數(shù)，其定義為直方圖和模型分布之間的K－L距離或相對熵（ΔH）與直方圖分布的熵值（H）的比值，其值越小說明擬合得越好。

圖3 VisTex數(shù)據(jù)庫中的典型實驗圖像

由圖4可知，對于高頻復值子帶的幅值系數(shù)，根據(jù)熵差率的數(shù)據(jù)，采用Weibull和Gamma分布進行統(tǒng)計建模比較準確，而采用GGD分布建模不太合理；相比較而言，Weibull分布建模由于初值選擇合理，收斂性較好，其擬合的熵差率最小，擬合效果最好。因此，選用Weibull分布模型的兩個參數(shù)作為幅值子帶的特征。

由圖4（a）和（d）的數(shù)據(jù)比較可知，兩個不同類紋理圖像的Weibull分布參數(shù)之間有著明顯的數(shù)值差異，因此特征間具有明顯的區(qū)分能力。可以預期，由于分布參數(shù)特征提取的準確性較高、區(qū)分性較好，從而能夠保證檢索系統(tǒng)的性能得到有效的改善。

3.2 相對相位子帶系數(shù)的統(tǒng)計模型選擇

同樣地，為了比較，隨機選用VisTex數(shù)據(jù)庫［5］中的Fabric.0007和Fabric.0009作為典型的實驗圖像，如圖5所示，并對其進行3層DTCWT變換。針對第1層的－75°高頻復值子帶的相對相位系數(shù)分別進行von Mises分布、wrapped Cauchy分布和Vonn分 布 建 模［9，16］和 直 方 圖 擬 合。Fabric.0007、Fabric.0009圖像的實驗結果分別如圖6（a）～（c）、（d）～（f）所示，各分布圖下括號里的數(shù)值分別為位置參數(shù)、尺度參數(shù)和熵差率。

由圖6可知，對于高頻復值子帶的相對相位系數(shù)，根據(jù)直方圖擬合的效果及熵差率的大小，3種分布模型的擬合效果差別并不太大，相比較而言，wrapped Cauchy分布的建模準確性較高。并且，與VisTex數(shù)據(jù)庫所有圖像擬合的平均效果相比，wrapped Cauchy分布的模型擬合效果要優(yōu)于其他兩個模型分布。因此，選擇wrapped Cauchy分布對相對相位系數(shù)進行建模，并以此分布參數(shù)作為相對相位子帶的特征。

由圖6（b）和（e）的數(shù)據(jù)比較還可知，兩個比較接近的不同類紋理圖像的wrapped Cauchy分布參數(shù)之間也有著明顯的數(shù)值差異，特征間的區(qū)分能力較好，從而有助于提高檢索系統(tǒng)的性能。

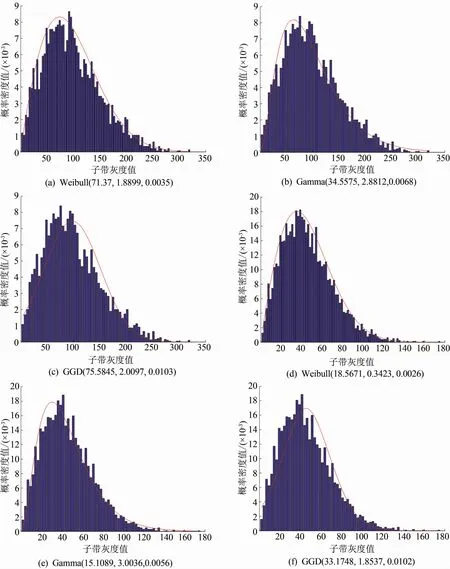
圖4 幅值子帶系數(shù)的統(tǒng)計建模圖

圖5 VisTex數(shù)據(jù)庫中的典型實驗圖像

圖6 相對相位子帶系數(shù)的統(tǒng)計建模圖

3.3 分解層數(shù)的選擇

對于用于圖像統(tǒng)計建模的多尺度變換，分解層數(shù)的選擇應保證最小子帶圖像尺寸≥16 pixel×16 pixel。否則，對所估計的子帶能量值及模型參數(shù)值的準確性都會產(chǎn)生不良的影響。由于實驗中選擇的是VisTex紋理圖像庫，所采用的每類子圖像大小為128 pixel×128 pixel，因此選擇的最大分解層數(shù)為3層。能量特征和幅值子帶統(tǒng)計特征都是根據(jù)DTCWT分解成3層而提取的。

對于相對相位子帶特征的提取，所需的最佳分解層數(shù)并沒有具體的依據(jù)。為此，僅針對相對相位特征，分別進行了DTCWT的1～3層分解的紋理圖像檢索實驗，平均檢索率依次為72.01%、77.42%、73.96%。因此，從最佳檢索性能角度出發(fā)，相對相位特征提取采用的分解層數(shù)為2層。

綜上分析，最終采用的實驗方案為：對于能量特征，選擇3層DTCWT分解，每層取1個概貌子帶，特征數(shù)為3×1×2＝6；對于幅值特征，選擇3層DTCWT分解，每層取6個幅值子帶，特征數(shù)為3×6×2＝36；對于相對相位特征，選擇3層DTCWT分解的前2層，每層取6個相對相位子帶，特征數(shù)為2×6×2＝24。最后，實驗所取的總特征數(shù)為66。

3.4 不同方法的檢索性能比較

根據(jù)提出的檢索方法，以平均檢索率為性能指標，通過與其他典型檢索方法的最好結果進行性能比較說明其有效性。選用這些方法進行比較的原因，是因為其采用了與文章相同的紋理圖像數(shù)據(jù)庫以及檢索性能評價指標，并且多尺度變換均采用3層分解。其中，L1＋L2方法采用的特征是實小波子帶的均值和方差，相似性測度采用歸一化歐氏距離［5］。GGD方法采用的特征是實小波變換域細節(jié)子帶系數(shù)的GGD分布參數(shù)，相似性測度采用K－L距離［5］。GGD－WC方法的特征采用均勻離散Curvelet復變換實部和虛部子帶的GGD分布參數(shù)、相對相位子帶的wrapped Cauchy分布參數(shù)，相似性測度采用K-L距離［16］。GGD-Vonn方法的特征采用均勻離散Curvelet復變換實部和虛部子帶的GGD分布參數(shù)、相對相位子帶的Vonn分布參數(shù)，相似性測度采用K-L距離［9］。Copula方法的特征采用Copula聯(lián)合統(tǒng)計建模的分布參數(shù)，相似性測度采用K－L距離［10］。Ves方法的特征采用小波框架變換域細節(jié)子帶的廣義Gamma分布參數(shù)和相位的廣義von Mises分布參數(shù)，相似性測度采用加權的對稱K－L距離［13］。Yang方法的特征采用無下采樣Contourlet變換域方向子帶的Weibull分布參數(shù)，相似性測度采用K－L距離［7］。

采用上述方法得到的平均檢索率依次為64.83%、75.73%、85.64%、85.82%、83.58%、80.78%了86.74%，具有更好的檢索性能。由于在DTCWT多尺度多方向復變換域，文章方法對圖像的所有子帶統(tǒng)計信息都進行了充分的利用，并通過多特征互補融合有效地刻畫了紋理圖像的方向分布特征。同時，最優(yōu)地利用了相似性測度的加權組合，從而有效地改善了紋理圖像檢索系統(tǒng)的性能。

4 結論

通過上述研究，得到如下結論：

（1）由于采用了多類系數(shù)統(tǒng)計特征的互補融合，使圖像的所有子帶統(tǒng)計信息都得到了充分的利用，紋理圖像的方向分布特征也得到了有效的刻畫。同時，通過利用最優(yōu)的相似性測度加權組合，從而顯著地提高了紋理圖像檢索系統(tǒng)的平均檢索率。

（2）以平均檢索率為性能指標，通過和其他7種典型檢索方法的最好結果進行性能比較，文章中提出的方法獲得了可達86.74%較高的平均檢索率。