應用改進的Levenberg-Marquardt方法求解一類多線性系統
王 麗,陳 震,劉奇龍
(貴州師范大學數學科學學院,貴州貴陽550025)
1 預備知識
設A是一個m階n維的張量,表示為
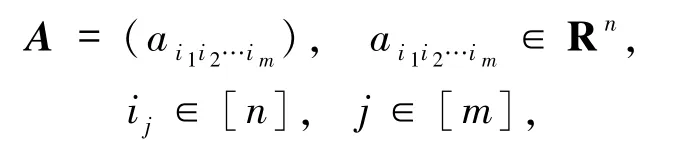
其中,[n]={1,2,…,n}.稱張量A是對稱的,如果ai1i2…im=aπ(i1i2…im),?π∈Πm,其中Πm是指標向量[1,2,…,m]的所有排列的全體.稱張量A是半對稱的,如果

其中Πm-1是指標向量[2,3,…,m]的所有排列的全體.
本文考慮如下多線性系統的數值求解問題

其中,x=[x1,x2,…,xn]T∈Rn是未知向量,Axm-1是列向量,它的第i個元素定義為
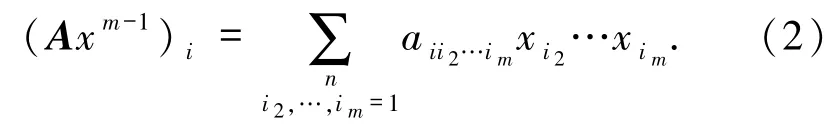
多線性系統(1)來源于數據挖掘、微分方程數值解和張量補等實際問題[1-3],近年來受到廣泛關注.2015年,Li等[1]提出了求解數據挖掘背景下產生的系數為稀疏非負張量的多線性系統的一種迭代方法,并證明了算法的線性收斂性;2016年,Ding等[2]研究了系數張量為M-張量的多線性系統,在張量A是非奇異的M-張量,b是正向量的情形下證明了方程有唯一的正解,并提出了求解張量方程的幾種迭代算法,推廣了經典的Jacobi方法與Gauss-Seidel方法;Han[4]提出了確定這個唯一正解的同倫方法;He等[5]提出了二次收斂的Newton型算法;2017年,Li等[6]將一些經典的分裂方法推廣到求解對稱張量方程,在適當的條件下證明了算法的全局收斂性和局部r-線性收斂性;對于系數為強M-張量的張量方程,Liu等[7]提出了一些基于張量分裂的算法,并將該算法應用到高階馬爾可夫鏈模型;Lü 等[8]將經典的 Levenberg-Marquardt(LM)方法應用到系數為半對稱張量的多線性系統,并證明了在局部誤差界下的全局收斂性與局部二次收斂性;Li等[9]提出了求解多線性系統的混合交替投影算法,并證明了在適當條件下算法的局部線性收斂性.
綜上,現有方法通常是針對系數為對稱或半對稱的張量或具有一定結構的非奇異M-張量的多線性系統進行討論.本文則是考慮一般情形下的多線性系統(1).首先討論了應用改進的LM方法求解多線性系統的數值算法,然后證明了該方法在局部誤差界條件下的全局收斂性和局部二次收斂性,最后通過數值算例驗證了該方法的有效性.
2 迭代算法



3 收斂性分析



4 數值算例
選取幾個例子驗證算法2.2的有效性.所有程序在配置為intel(R)Core(TM)i5-6200U CPU @2.30 GHz的筆記本電腦環境下使用Matlab 2015b編寫,涉及到張量計算的部分使用了工具箱Tensor toolbox 2.5[16].迭代過程中的容許誤差取為,其中算法2.2相關參數的選取為:α0=0.5,αmin=1.0×10-5,a1=4,a2=1/4,h0=0.02,h1=0.3,h2=0.6,最大迭代次數N=20.
例4.1采用文獻[8]中的例5.1,考慮多線性系統(1).首先生成一個m階n維隨機非負張量A,其元素在(0,1)上均勻分布.為了得到向量b,先選取x*=2*ones(n,1)為準確解.在實驗中選取初值x0=3*ones(n,1),通過算法2.2 計算多線性系統的解,并與文獻[8]的算法相比較.數值結果如表1所示,其中,k表示迭代次數,t表示運算時間,∈res表示相對誤差‖x-x*‖/‖x*‖.因為這里的張量A沒有對稱性,所以不能直接使用文獻[8]的LM方法.為了與文獻[8]中的LM方法比較,在計算Jacobi矩陣時不能利用文獻[8]中的(3.4)式,而是利用本文的(8)式.由表1可以看出:算法2.2與LM方法相比較,前者所需的迭代次數更少,時間更短.

表1 選取不同階數不同維數的多線性系統的數值結果Tab.1 The numerical results of multilinear systems with different orders and dimensions
圖1是選取m=4,n=30時,算法2.2的收斂性演示.顯然,在局部誤差界條件下,算法2.2產生的點列是二次收斂的.
下面利用數值實驗說明該方法可應用于如下廣義的多線性系統

其中,Ap是一個p階n維的張量,p=2,3,…,m.
例4.2隨機產生一個三階張量A1和二階矩陣A2,其元素都在(0,1)上均勻分布,選取
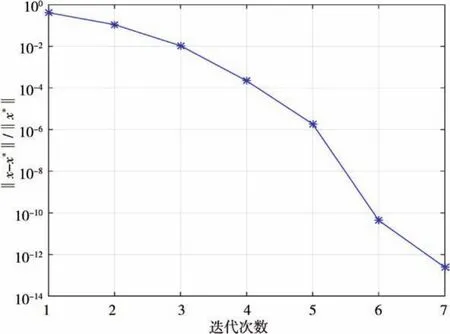
圖1 算法2.2的收斂性演示Fig.1 Convergence demonstration of Algorithm 2.2
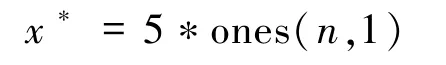
為準確解,從而確定右端向量b.利用算法2.2求解上述的多線性系統,結果如表2所示.表2表明算法2.2同樣可以有效求解廣義的多線性系統.
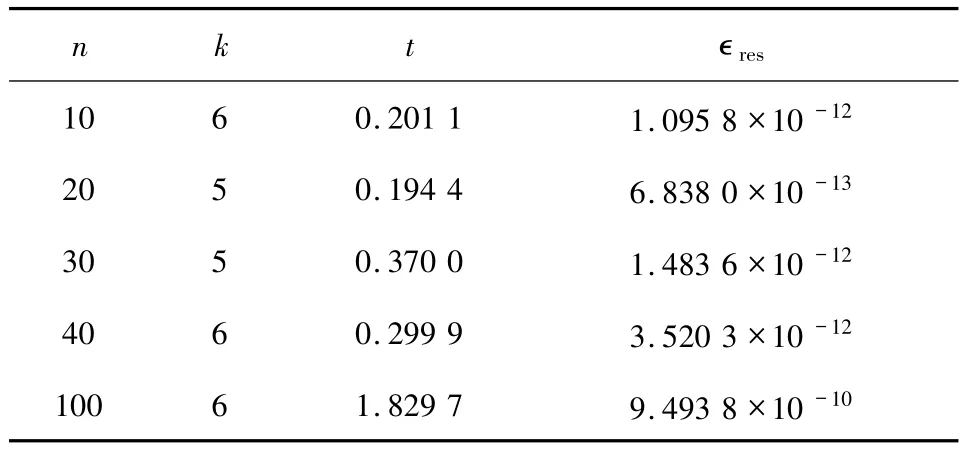
表2 選取不同維數的廣義多線性系統的數值結果Tab.2 The numerical results of generalized multilinear systems with different dimensions
例4.3參考文獻[2]中的例4.3,考慮引力作用下的質點運動方程
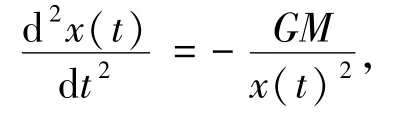
Dirichlet邊界條件為
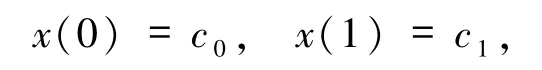
其中重力常數G≈6.67×10-11Nm2/kg2和地球質量M≈5.98×1024kg.
離散化后可以得到如下的多項式方程組
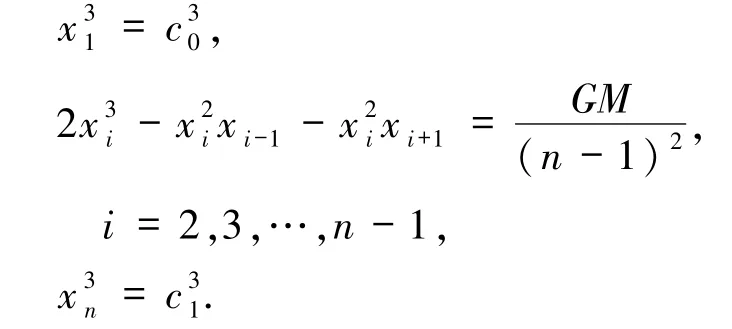
上述方程組可以改寫成多線性系統Ax3=b,其中系數A是一個四階張量,其元素為
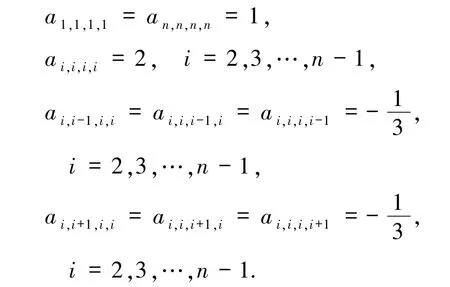
右端向量b中的元素為
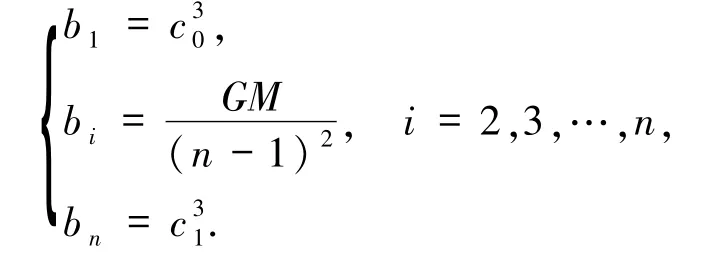
另一方面,質點運動軌跡可以用拋物線近似地表示

其中,c0和c1表示地球半徑,等于6.37×106km,重力加速度g≈9.8 m/s2,α和β是由邊界條件確定的常數.
圖2是利用算法2.2求解上述多線性系統的數值結果與拋物線的對比,顯然,數值結果完全符合實際情況.

圖2 在引力作用下質點運動的軌跡Fig.2 Trajectory of particle motion under the action of gravity

