一類分數階p-Laplacian奇異邊值問題解的存在性
2020-07-05 09:18:38王和香胡衛敏
四川師范大學學報(自然科學版) 2020年1期
王和香,胡衛敏
(1.喀什大學數學與統計學院,新疆喀什844006; 2.伊犁師范學院數學與統計學院,新疆伊寧835000)
0 引言
非連續介質電動力學、系統辨識、材料力學、自動控制、分形混沌、信號處理和神經網絡(ANN)等方面的許多問題都涉及到分數階微分方程的應用.在研究微分方程理論及其邊值問題,尤其是非局部邊值問題時,分數階模型比整數階模型更貼切,提供的方法也更靈活多樣.
文獻[1]利用不動點定理和Green函數的性質,考慮在無窮區間上含p-Laplacian算子的分數階微分方程m點邊值問題

文獻[2]利用錐上的不動點定理,研究一類奇異含無窮點邊值條件的微分方程邊值問題
由于p-Laplacian算子作為傳統Laplacian算子的推廣,p-Laplacian在電動力學、熱傳導理論和量子力學等方面有著大量的應用,因此,對含p-Laplacian算子的分數階微分方程的研究已經成為研究熱點.文獻[3]利用上下解方法,結合Schauder不動點定理,分析一類具p-Laplacian算子的高階奇異無窮多點邊值問題
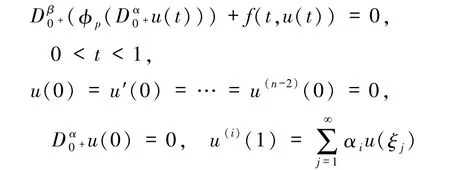
解的存在性,其中,n-1<α<n(n≥3),0<β≤1,0<ξj<1(j=1,2,…).
受以上文獻啟發,本文將研究一類含p-Laplace算子的奇異邊值問題

1 預備知識與引理


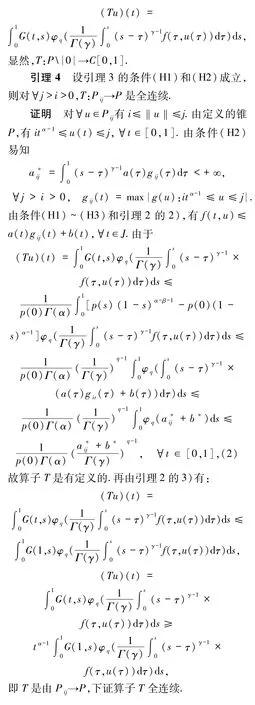

2 主要結論


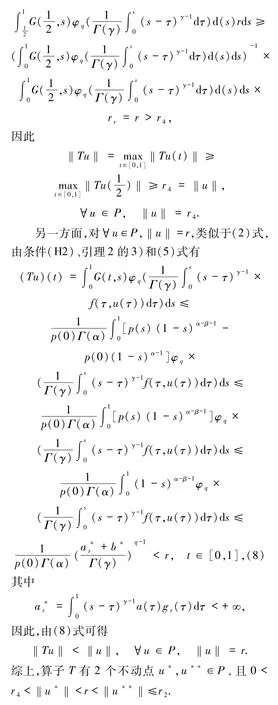
3 舉例
考慮無窮點邊值問題


致謝喀什大學校內課題(16)2588對本文給予了資助,謹致謝意.
猜你喜歡
中等數學(2022年2期)2022-06-05 07:10:50
體育科技文獻通報(2022年3期)2022-05-23 13:46:54
中學生數理化·七年級數學人教版(2021年11期)2021-12-06 05:38:48
天津外國語大學學報(2021年3期)2021-08-13 08:32:18
遼金歷史與考古(2021年0期)2021-07-29 01:06:54
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
科技傳播(2019年22期)2020-01-14 03:06:54
民用飛機設計與研究(2019年4期)2019-05-21 07:21:24
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10

