壓力下HfCr2合金的電子結構和彈性性質

于家輝，宋金璠，陳蘭莉，濮春英，張飛武，周大偉

（1.南陽理工學院電子與電氣工程學院，河南南陽473004； 2.南陽師范學院物理與電子工程學院，河南南陽473061；3.中國科學院地球化學研究所礦床地球化學國家重點實驗室，貴州貴陽550081； 4.蘇州科技大學數理系，江蘇蘇州215009；5.科廷大學納米化學研究所，澳大利亞珀斯WA6845）

鉿合金具有許多優異的特性，它在航空、核能、包套材料和醫學等領域有著非常廣泛的應用，其潛在的應用價值巨大.鉿合金具有抗高溫和抗高壓的特性［1-2］，是可以用在發動機和導彈上的結構材料；鉿合金的析出會改善材料的強度［3-4］；鉿合金同時具有生物相容性和抗腐蝕的特性，從而被應用于醫療植入物和醫療設備的制造［5］；鉿合金可能是潛在的記憶合金［6］.此外，室溫下鉿合金與氫能夠形成含氫量很高的化合物，因此，它被認為是一種良好的儲氫能源材料［7］.

Venkatraman等［8］通過對基于金相、X射線衍射和熱分析技術而得到的HfCr合金相圖的分析表明，低溫下HfCr2的MgCu2類型立方相是穩定的，而在高溫MgZn2類型的六角相是穩定的，進一步研究表明，因為從低溫到高溫的相轉變是緩慢的，所以2種相的相轉變溫度很難準確測定.Alisova等［9］分別在1 000和1 100℃下對HfCr2合金進行退火，退火時間分別為75和50 h.最后對樣品的分析表明，通過電弧熔煉法制備的高溫下穩定的MgZn2類型六角相緩慢轉變成低溫下穩定的MgCu2類型的立方相.Carlson和Alexander［10］利用X射線衍射和熱分析技術研究了利用電弧熔煉法獲得的Hf-Cr合金系統，對獲得的Hf-Cr系統相圖的研究表明，低溫下HfCr2的MgCu2類型立方相是穩定的，而在高溫MgZn2類型的六角相是穩定的.但是，同樣難以準確測定2相轉變的溫度.Rudy和 Windisch［11］利用金相、X 射線衍射和熱分析技術研究了Hf-Cr合金樣品，結果表明HfCr2合金高溫下穩定的MgZn2類型六角相是存在的，但其研究結果無法說明低溫下MgCu2類型的立方相的存在.文獻［12］利用電弧熔煉法制備了HfCr2的萊夫斯相合金，然后在不同溫度范圍內退火，最后利用XRD衍射、電子衍射和高分辨透射電子顯微鏡對實驗樣品進行分析，發現一直到1 150℃左右立方相結構都是穩定的，而在更高的溫度MgZn2類型的六角相是穩定的.Chen等［13］利用從頭化算法主要研究了HfCr2合金的MgCu2類型立方相和MgZn2類型的六角相的基態物理性質，具體包括基態的結構參數、相的穩定性、形成焓、彈性性質和電子結構.穩定性的研究表明從低溫一直到接近熔點的高溫范圍內立方相的HfCr2合金都是穩定的，而六角相的Hf-Cr2合金則出現在高溫范圍內.到目前為止，對HfCr2合金立方相和六角相結構在通常條件下和一定壓力下的結構穩定性、電子結構、脆性與延展性、彈性各向異性等作為合金材料的重要物理特性還沒有系統的研究，這勢必會影響對HfCr2合金材料的進一步應用.近年來，基于密度泛函理論的第一原理方法在對晶體的物性研究、結構預測和材料設計等方面取得了巨大進展［14-25］，本文采用此方法并結合CASTEP軟件包［26］，對HfCr2合金在一定壓力下的2相的物理性質進行了系統研究.從力學和熱力學角度研究了2相的結構穩定性；計算了合金的電子結構、彈性常數，給出了合金的體模量、剪切模量和楊氏模量隨壓力的變化，并對其彈性各向異性和泊松比進行了分析；還給出HfCr2合金2種相結構的應力-應變曲線關系，分別指出了2種結構理想拉伸和剪切強度出現的方向.上述研究為HfCr2合金的潛在應用提供了知識儲備，為實驗上制備和加工該合金材料提供了理論指導.

1 計算方法

對HfCr2合金2個相的研究由CASTEP軟件實現.該軟件采用密度泛函平面波贗勢方法，通過它可以對陶瓷、半導體和金屬等多種晶體材料進行第一原理計算，而第一性原理是一種在電子層面對材料進行模擬計算的研究方法［27］，它的廣義梯度近似方法GGA已被廣泛應用于晶體材料的理論計算［26］.本文計算采用非局域超軟贗勢理論［28］（USPP）處理離子實、價電子之間的相互作用，采用PBE-GGA［29］描述電子間的交換關聯作用.通過收斂測試確定平面波動能的截斷值為410 eV，此時體系的總能可以收斂到5×10-6eV/atom.Hf原子的贗勢采用5d26s2共4個價電子，Cr原子的贗勢采用3d54s1共6個價電子.布里淵區K點采用Monkhorsyt-Pack K點網格選取法［30］，對立方相采用5×5×5的K點網格，六角相采用8×8×4的K點網格完成計算，此時采用上述K點網格，單胞的總能可以收斂到5×10-6eV/atom.對晶格常數和彈性常數的測試表明，進一步增加截斷能和K點網格并不會給出不同的物理結果.本文還借助CASTEP軟件并利用贗勢平面波技術對HfCr2合金的2個相進行Mulliken原子布居分析，計算中將Hf原子5d26s2態電子和Cr原子的3d54s1態電子視為價電子.

2 結果和討論

2.1 HfCr2合金相結構及其穩定性 采用全弛豫的結構優化方法得到了0 GPa下HfCr2合金2相結構的晶格參數.與立方相晶胞對應的空間群為Fd 3—m，晶格常數的實驗值為0.716 0 nm［10］，理論計算的晶格常數值是0.706 5 nm.六角相晶胞的空間群為P63/mmc，晶格常數的實驗值為a＝b＝0.507 7 nm，c＝0.825 4 nm［31］，計算得到的晶格常數a＝b＝0.502 3 nm，c＝0.807 9 nm.2種相結構優化后的晶格常數與實驗值相比誤差均小于3%，表明計算值與實驗值符合的很好，計算所得的六角相晶格常數與文獻［12］給出的結果符合的也很好，為進一步的理論計算提供了可靠的依據.本文首先研究了2相在0～20 GPa范圍內的熱力學穩定性.在零溫和一定壓力下，比較2個結構的熱力學穩定性，主要比較焓值，即

H ＝E+pV，

其中E、p和V分別是體系的總能、壓強和體積.在給定壓強p的情況下，通過第一原理可以計算出內能E，通過結構弛豫可以給出體積V，進而可以算出焓H的值.圖1是HfCr2合金2相的焓曲線，顯示在0～20 GPa范圍內，立方相結構的能量始終低于六角相結構，表明在此壓力范圍內HfCr2合金立方相要更加穩定，而六角相則為亞穩態結構.

2.2 電子結構 圖2中（a）和（b）是2種相結構下HfCr2合金在布里淵區沿高對稱方向的能帶，而（c）和（d）則給出了相應結構的態密度.在合金的能帶結構圖中，可以看到費米面附近價帶和導帶都發生了重疊，因此，2種結構下的合金都呈現出金屬性.進一步研究發現，在合金的費米能級附近都出現了一個態密度值大于0的低谷，即所謂出現了“贗能隙”.一般用贗能隙將成鍵態和反鍵態區分開來，它的出現通常意味著共價鍵特性的存在，并且認為費米能級處的態密度值越小，該體系的結構穩定性越好.

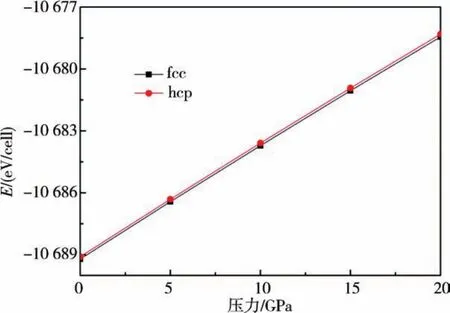
圖1 HfCr2合金的焓與壓力的關系Fig.1 The calculated enthalpies of HfCr2alloy as a function of pressure

從態密度上可以看出，在費米能級處立方相結構總態密度值要小于六角相結構，所以立方相結構要更為穩定，這同前面能量計算的結果相一致.另外需要指出的是，2種相結構在費米能級處的態密度值都不為零，所以二者都表現出金屬特性，這同上面能帶分析給出的結論相吻合.2種相結構的主要成鍵峰都落在-4～0 eV之間，結合分波態密度圖在費米能級附近可以發現，-2～0 eV之間成鍵態主要源自于Hf（Cr）原子p態和d態的貢獻，并且Cr原子p態和d態對成鍵態貢獻要更大一些，而源自Hf和Cr原子s態的貢獻幾乎可以忽略，但是在-4～-2 eV之間，Hf和Cr原子s態對成鍵態的貢獻則較為明顯.反鍵態主要落在0～2 eV之間，主要貢獻來自Hf（Cr）原子的d態，而相應p態的貢獻則非常小.2個結構都表現出類似的電子結構特點，即Hf的5d態對反鍵態有一定貢獻，但是Cr原子3d態貢獻更大.總體上可以看出Hf（Cr）原子的p態和d態對費米能級處態密度均有貢獻，表現出一定的p-d軌道雜化行為.

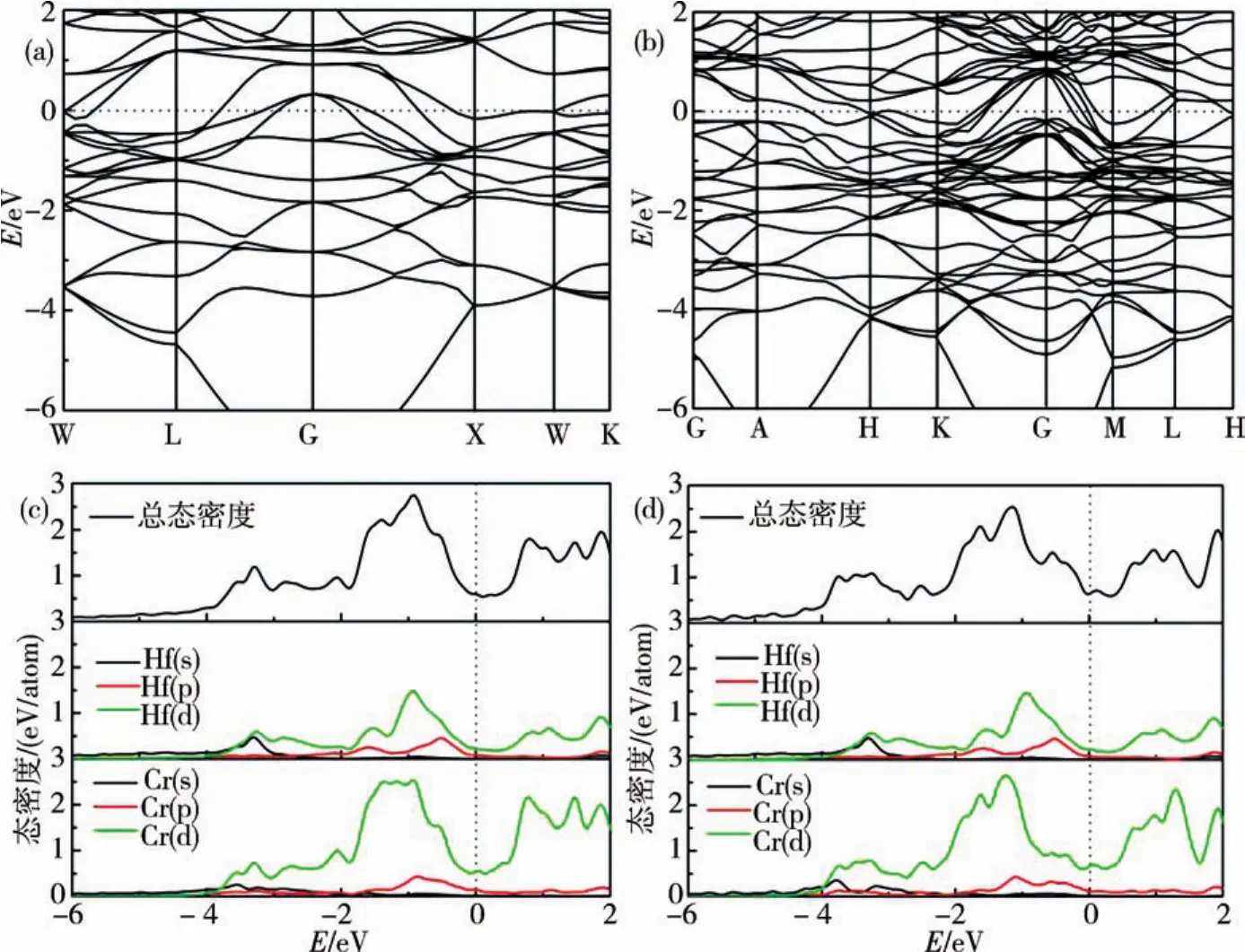
圖2 0 GPa時HfCr2合金的能帶結構、總態密度和分波態密度圖Fig.2 The electronic energy band structures，and the total and partial density for HfCr2alloy at 0 GPa

表1為特定壓力下HfCr2合金立方相和六角相的Mulliken原子布居分析.從表1中可以看出，對于HfCr2合金的2種相而言，隨著壓力的增加，電荷都從Cr原子遷移到Hf原子，且越來越多.對立方相的具體分析發現，在壓力從0 GPa增加到5 GPa和壓力從15 GPa增加到20 GPa的2種情況下，電荷從Cr的p態向Cr的s和d態遷移，還有一部分電荷遷移到Hf的p態和d態；而在壓力從5 GPa增加到10 GPa和壓力從10 GPa增加到15 GPa的2種情況下，電荷從Cr的p態向Cr的s和d態遷移，另一部分電荷則向Hf原子的s、p和d態遷移.對六角相的具體分析表明，在壓力從0 GPa增加到5 GPa和壓力從10 GPa增加到15 GPa的2種情況下，電荷從Cr1和Cr2原子的p態遷移到s態和d態，另一部分電荷則遷移到 Hf原子的 s、p和 d態；當壓力從5 GPa增加到10 GPa，電荷從Cr1和Cr2原子的p態遷移到Cr2的s態和d態，另一部分遷移到Cr1的s態，最后一部分電荷則遷移到Hf原子的 s、p和d態；當壓力從15 GPa增大到20 GPa，電荷從Cr1和Cr2原子的p態遷移到Cr2的s態和d態，另一部分電荷遷移到Cr1的d態，最后一部分電荷則遷移到Hf原子的s、p和d態.

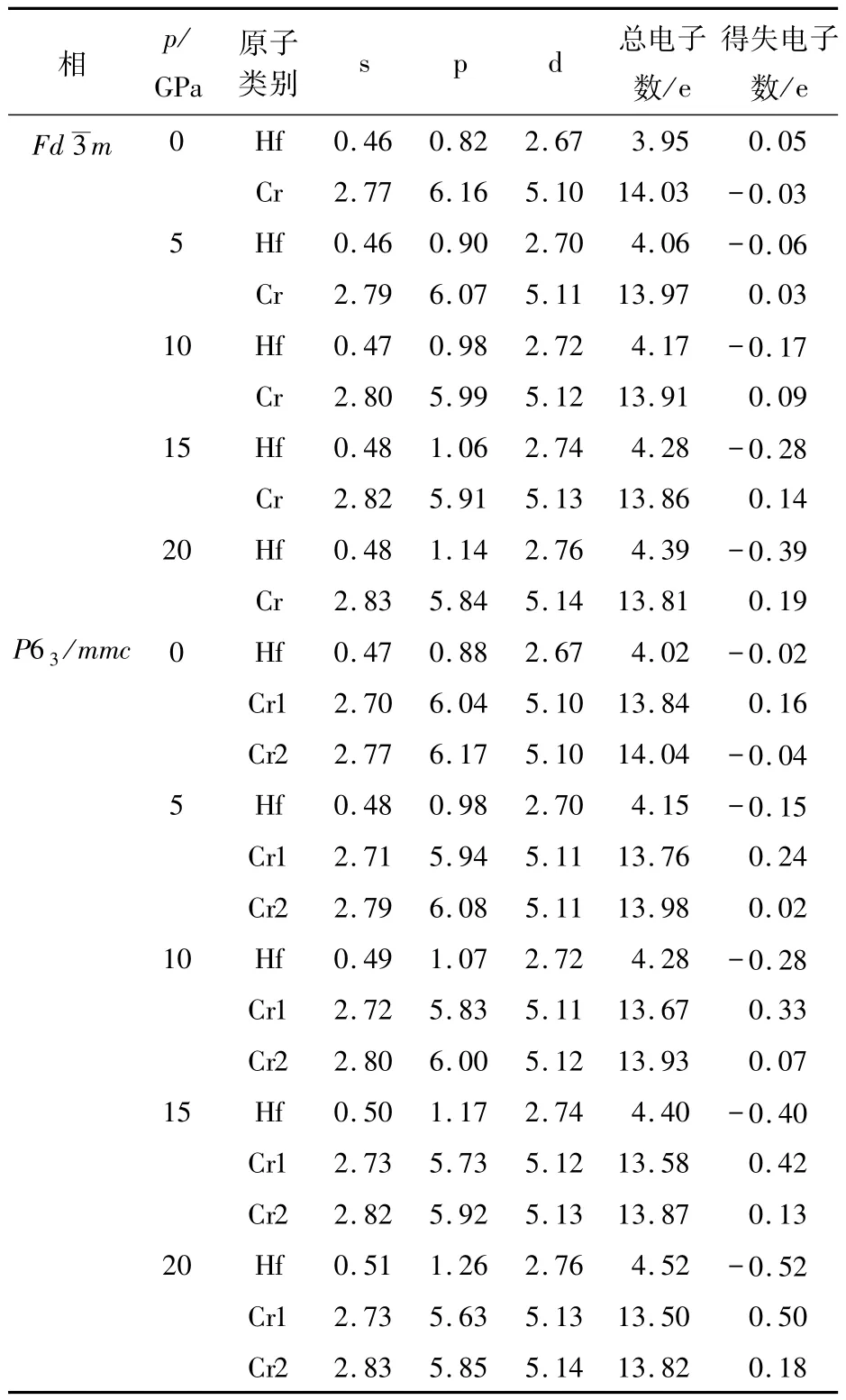
表1 特定壓力下HfCr2合金立方相和六角相的Mulliken原子布居分析Tab.1 Mulliken atomic population analysis of fcc phase and hcp phase for HfCr2alloy at selected pressures

2.3 壓力下的彈性性質 研究合金的彈性常數有助于理解其機械和物理性能.本文利用應力-應變法求出了2種結構的彈性常數.表2給出了本文計算所得到的HfCr22種相結構的彈性常數值，同時還給出了其他的理論計算結果.通過對比發現，本文計算結果與其他人的計算結果總體上符合較好.

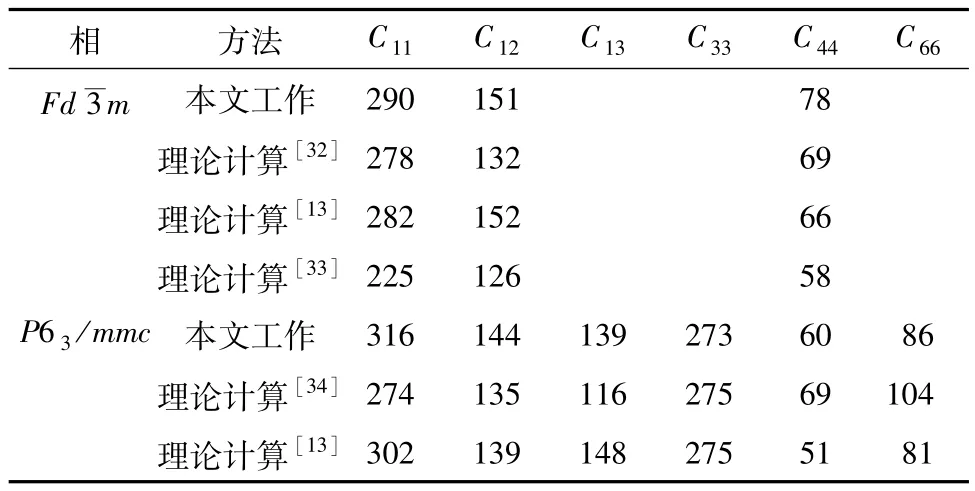
表2 HfCr2合金立方相和六角相的彈性常數以及其他的理論計算結果Tab.2 Calculated elastic constants（GPa）of fcc phase and hcp phase for HfCr2alloy，together with other theoretical values

圖3（a）給出了立方相的彈性常數與壓力的關系，研究發現在整個壓力范圍內，立方相合金滿足力學穩定性條件［35］：C11＞ 0，C44＞0，C11＞ ｜C12｜，（C11+2C12）＞0，即立方相結構在研究的壓力范圍內滿足力學穩定性要求.同時還發現立方相合金的3個彈性常數都隨壓力的增加而呈逐漸增大的趨勢，但總滿足C11＞C12＞C44，其中 C11值最大，表明合金對沿著主軸方向抵抗彈性形變的能力最大，C44最小則意味著體系沿著（1 0 0）平面抵抗剪切彈性形變的能力相對較弱.圖3（b）給出的是六角相合金彈性常數與壓力關系，在整個壓力范圍內六角相合金的彈性常數滿足力學穩定性條［36］：C12＞0，C33＞0，C11＞ ｜C12｜，C44＞ 0，（C11+2C12）C33＞ 2C213.因此，六角相結構在力學上是穩定的，從中還可以看出在整個壓力范圍內彈性常數值均隨壓力的增加而增大，且C11和C33的值始終要大于C44，表明合金沿著主軸方向的彈性形變難度要更大.而C44最小表明六角相結構合金沿著（1 0 0）平面抵抗剪切彈性形變的能力相對較弱.

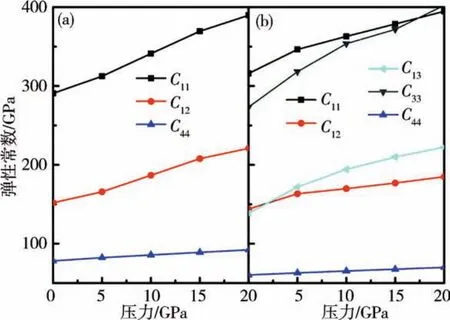
圖3 HfCr2合金彈性常數隨壓力的變化Fig.3 Pressure dependence of elastic constants for HfCr2alloy

合金的體模量B、剪切模量G和楊氏模量E等彈性性質也是描述合金性質的重要物理量.由立方相和六角相合金模量與彈性常數關系［37-38］，可以得到Voigt近似和Reuss近似下的BV、GV、BR及GR的表達式，再通過Hill近似［39］最終得到合金的體模量B、剪切模量G和楊氏模量E的計算公式：

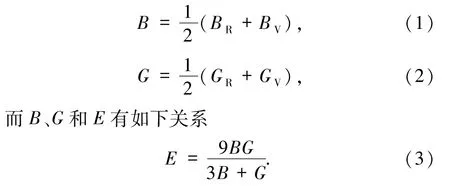
下標V表示Voigt近似結果，R表示Reuss近似結果.表3給出了2種相結構的體模量、剪切模量和楊氏模量的值，通過與其他理論和實驗研究工作給出的結果進行對比發現，總體上看符合的較好.

表3 HfCr2合金的體模量B、剪切模量G、楊氏模量E、泊松比ν和普格模量比G/BTab.3 Bulk modulus B（GPa），shear modulus G（GPa），Young's modulus E（GPa），Poisson's ratio ν and Pugh's modulus ratio G/B for HfCr2alloy

圖4 HfCr2合金體模量B、剪切模量G和楊氏模量E隨壓力變化Fig.4 Pressure dependence of bulk modulus B，shear modulus G and young’s modulus E for HfCr2alloy

圖4給出了2種相結構合金彈性模量同壓力的關系.在整個壓力范圍內，2種相結構的體模量B、剪切模量G和楊氏模量E均隨著壓力的增加而單調增加.對于2種結構而言，它們剪切模量的值比較接近，且在所有模量中始終保持最小，這表明2個相抵抗剪切的能力相當，并且都比較弱；同時還應注意到立方相的楊氏模量始終大于六角相的楊氏模量，這表明立方相結構抵抗單軸拉伸應力下彈性形變的能力要強于六角相.

2.4 合金的各向異性 對合金彈性各向異性的研究是非常重要的，因為它表征了晶體在不同方向上物理、化學特性相近的程度.目前已知的晶體都是彈性各向異性的，所以在晶體物理學或者工程學上對其各向異性的描述顯得尤為重要［40］.文中采用2種方法研究合金的彈性各向異性，一是引入普適的彈性各向異性因子AU，其定義式［41］為

若AU的值取0，則合金表現為各向同性；而取值越大，合金的各向異性將越強.二是引入體模量和剪切模量各向異性百分比AB和AG，其定義式［42］為：

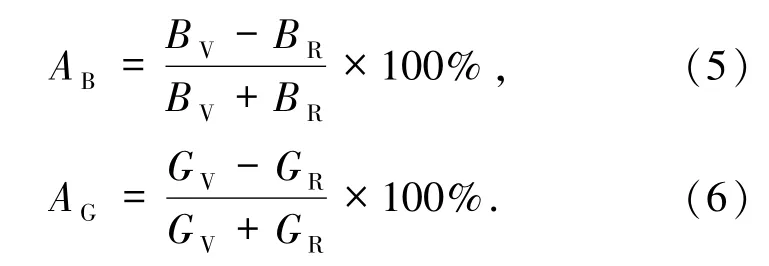
若AB和AG的值為0，則體模量和剪切模量表現出各向同性；若AB和AG的值取1，則表示體模量和剪切模量各向異性達到最強.圖5（a）給出了HfCr2合金的各向異性指數AU隨壓力變化的規律.在整個壓力范圍內：立方相各向異性指數AU的值很小，其表現出較強的彈性各向同性，且隨壓力的增長AU單調遞減，說明其彈性各向同性隨壓力增大而增強；而六角相各向異性指數AU的值始終比立方相要大，其表現出更強的各向異性，并且隨壓力的增長AU單調增大，因此六角相彈性各向異性隨壓力增大逐漸增強.圖5（b）則給出了合金的體模量和剪切模量各向異性百分比與壓力的關系.在研究的壓力范圍內：立方相結構AB的值為零，而AG的值始終都非常小，說明在立方相結構下體模量和剪切模量都表現出很強的各向同性；六角相結構AB和AG的值也都遠小于1，表明在該結構下體模量和剪切模量也表現出較強的各向同性，但在所有各向異性百分比值中，六角相的AG值始終最大，所以相對而言，六角相剪切模量的各向異性要更強一些.

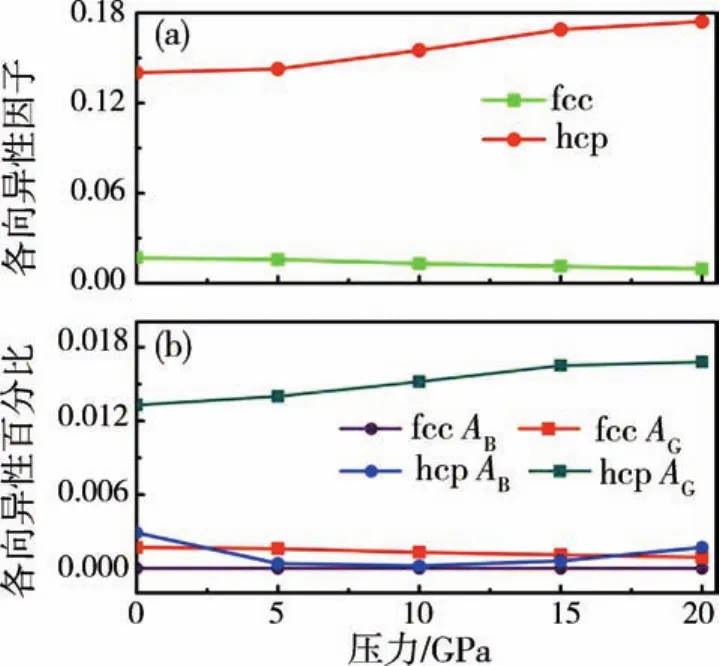
圖5 HfCr2合金（a）普適的彈性各向異性因子AU和（b）各向異性百分比AB、AG同壓力的關系Fig.5 Pressure dependence of（a）universal anisotropic index AU and （b）the percent anisotropy ABand AGfor HfCr2alloy

為了更系統地研究合金彈性模量各向異性，本文在圖6中給出了0 GPa下體模量和楊氏模量的三維（3D）方向示意圖.具體體模量和楊氏模量的計算公式［43］如下.

對于立方相有：

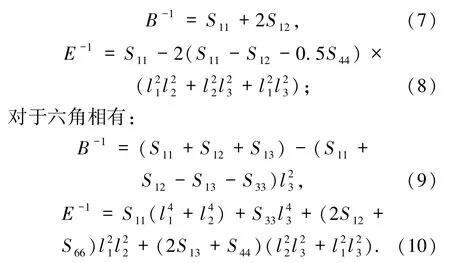
其中，Sij為彈性柔順常數，可以通過對彈性常數矩陣取逆得到，l1、l2和l3為方向余弦.對于各向同性系統而言，模量的3D方向示意圖將給出一個標準的球形；若是各向異性系統，模量的3D圖對于球形的偏離則反映出系統各向異性的程度.

圖6（a）中立方相合金體模量的3D圖為一個標準球形，即體模量表現出空間各向同性，與此前分析相一致；圖6（c）中六角相合金體模量的3D圖是一個沿著Bz方向因輕微形變而略扁的球，但其與標準球形相比偏離較小，因此體模量總體上仍然保持相對較強的各向同性；圖6（b）中立方相合金楊氏模量的3D圖與標準的球形存在著一定的偏離，但偏離程度較小，這說明楊氏模量總體上也呈現出空間各向同性；圖6（d）給出了六角相合金楊氏模量的3D圖，發現它較標準球形有更明顯的偏離，即其楊氏模量表現出一定的空間各向異性.

2.5 合金的脆性和延展性 脆性和延展性是合金屬性中非常重要的物理性質.在定量表征晶體材料脆性或者展性的方法中，具有普遍性的一種方法是由泊松提出的，即利用泊松比的值將材料定性歸類.泊松比的計算公式定義為：

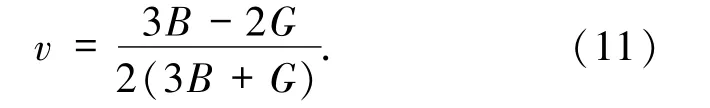
若泊松比大于0.3，物質表現出展性；反之則表現出脆性.另外一種常用的方法是基于Pugh提出的經驗表達式，即利用G/B的比值［44］判定材料脆性或延展性的本質.若比值小于0.5，合金的行為將表現出延展性的特征；反之，其行為將表現出脆性特征.如圖7（a）所示，0 GPa下2種相結構合金泊松比都大于0.3，表明2個合金相都呈現出延展性.泊松比隨著壓力的增加而增大，說明隨壓力增加2種合金的延展性有所提高，但研究表明六角相合金泊松比在整個壓力范圍內都大于立方相，這說明在研究的壓力范圍內六角相的延展性均要好于立方相.若用G/B的值來討論合金的延展性，如圖7（b）所示，所得結論與采用泊松比描述合金延展性給出的結論是一致的.表3中給出了前人計算所得到的立方相泊松比和普格模量比的值，其結果同樣表明立方相合金呈現出延展性.

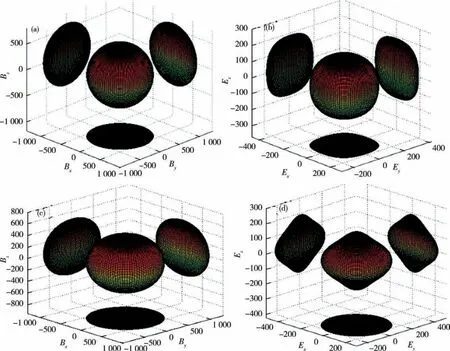
圖6 HfCr2合金依賴空間方位的體模量B和楊氏模量EFig.6 Directional dependence of the bulk modulus B（GPa）and directional dependence of the Young’s Modulus E（GPa）for HfCr2alloy

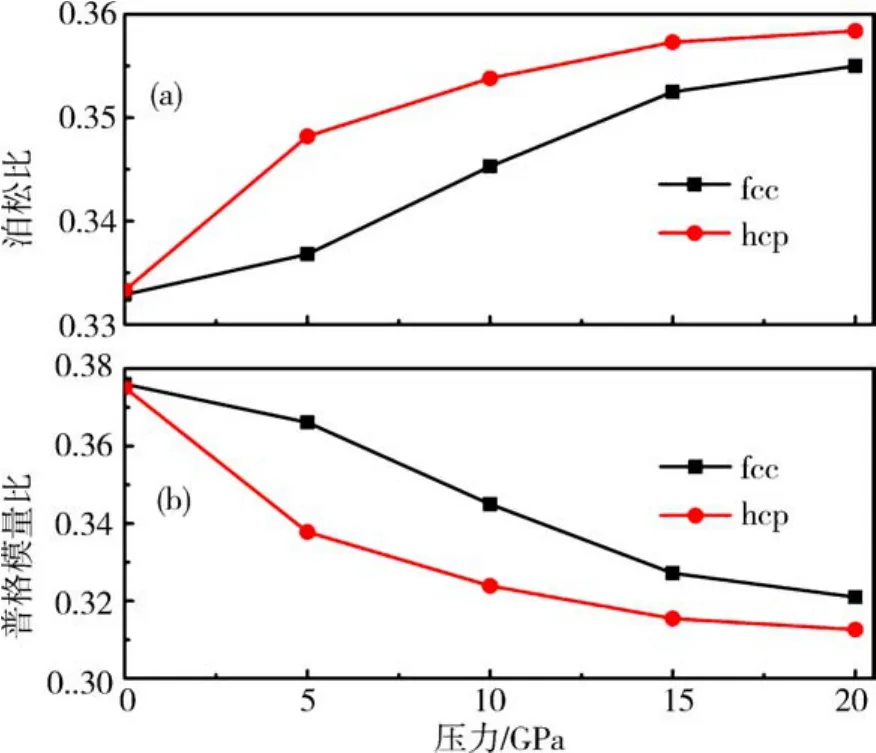
圖7 HfCr2合金（a）泊松比和（b）普格模量比G/B同壓力關系Fig.7 Pressure dependence of（a）Poisson’s ratios and （b）Pugh’s modulus ratios G/B for HfCr2alloy

2.6 應力-應變關系 材料的力學性能總是由缺陷所決定的，例如位錯和更復雜的斷裂，在無缺陷材料中斷裂與位錯形核的出現同理想的拉伸和剪切強度密切相關［45-46］，因此，研究理想的拉伸和剪切強度有著重要的意義.本文借助文獻［47-48］所描述的方法，計算了2種相結構的應力-應變關系，還討論了大應變下合金的力學性能.圖8（a）給出了立方相結構沿著［1 0 0］、［1 1 0］和［1 1 1］方向的單軸拉伸應力-應變曲線，原點附近小應變范圍內可以看到3條曲線幾乎重合，應力-應變曲線近似呈現線性關系.理論上，小應變下拉伸曲線線性部分的斜率，反映了楊氏模量在此方向上的強弱，據此可以看出0 GPa時該結構的楊氏模量有著較強的空間各向同性，這點與前面立方相楊氏模量3D圖給出的結果基本一致.隨著應變的增加，沿著3個方向的應力逐漸增加到最大值，分別為24.7、32.4和25.9 GPa，最大拉伸應力比約為1.0∶1.3∶1.0，大應變時拉伸強度各向異性較為明顯.在拉伸應力達到該方向應力極大值前立方相結構都是穩定的，此后隨著應變不斷增加，應力開始下降，結構開始變得不穩定.立方相結構理想的拉伸強度出現在［1 0 0］方向，其值為24.7 GPa.圖8（b）給出了立方相沿著（1 0 0）［0 0 1］、（1 0 0）［0 1 1］和（1 1 1）方向的剪切應力-應變曲線，圖中原點附近的曲線幾乎重合，應力隨應變增加近似線性增大，這表明剪切模量幾乎各向同性.沿3個方向最大剪切應力分別為23.4、20.7和19.0 GPa，相應比值約為1.2∶1.1∶1.0，此時的應變稱為臨界應變.應變較大時應力的各向異性體現得很明顯，沿著3個方向的應變分別超過各方向的臨界應變后，應力均隨應變增加逐漸減小，結構處于不穩定狀態.對于剪切應變而言，（1 1 1）方向為理想剪切強度出現的方向，其值為19.0 GPa.圖8中（c）和（d）分別給出了合金六角相結構拉伸和剪切情形下的應力-應變關系.如圖8（c）所示，在應變取值很小的區域內，結合數據可以發現相對于立方相而言，六角相沿著不同方向的拉伸曲線斜率有明顯差異，所以六角相楊氏模量的方向依賴性更強，這同前面給出的楊氏模量3D圖的分析結論相吻合.沿著和［0 0 0 1］方向的最大拉伸應力分別為32.5、26.8和25.2 GPa，對應的比值是1.3∶1.1∶1.0.大應變下應力的各向異性特征尤為突出.在3個方向的拉伸應力分別達到最大值前，六角相合金一直處于穩定狀態，之后隨應變增加結構開始變得不穩定.此結構合金的理想拉伸強度出現在［0 0 0 1］方向，其值為25.2 GPa.圖8（d）顯示，剪切應變取值在很小的范圍內時，相比于立方相結構剪切曲線而言，六角相沿著（0 0 0 1）和（0 0 0 1）方向的剪切曲線幾乎重合，表明在基面（0 0 0 1）內的剪切模量幾乎各向同性，而沿著方向的剪切曲線同其他2條曲線稍微有些分離，即該結構下的剪切模量表現出一定的空間各向異性.沿著方向最大剪切應力分別是21.4、19.7和17.8 GPa，對應比值是1.2∶1.1∶1.0，所以大應變時應力的各向異性特征更明顯.顯然沿著方向的最大剪切應力17.8 GPa為該結構下合金的理想剪切強度.

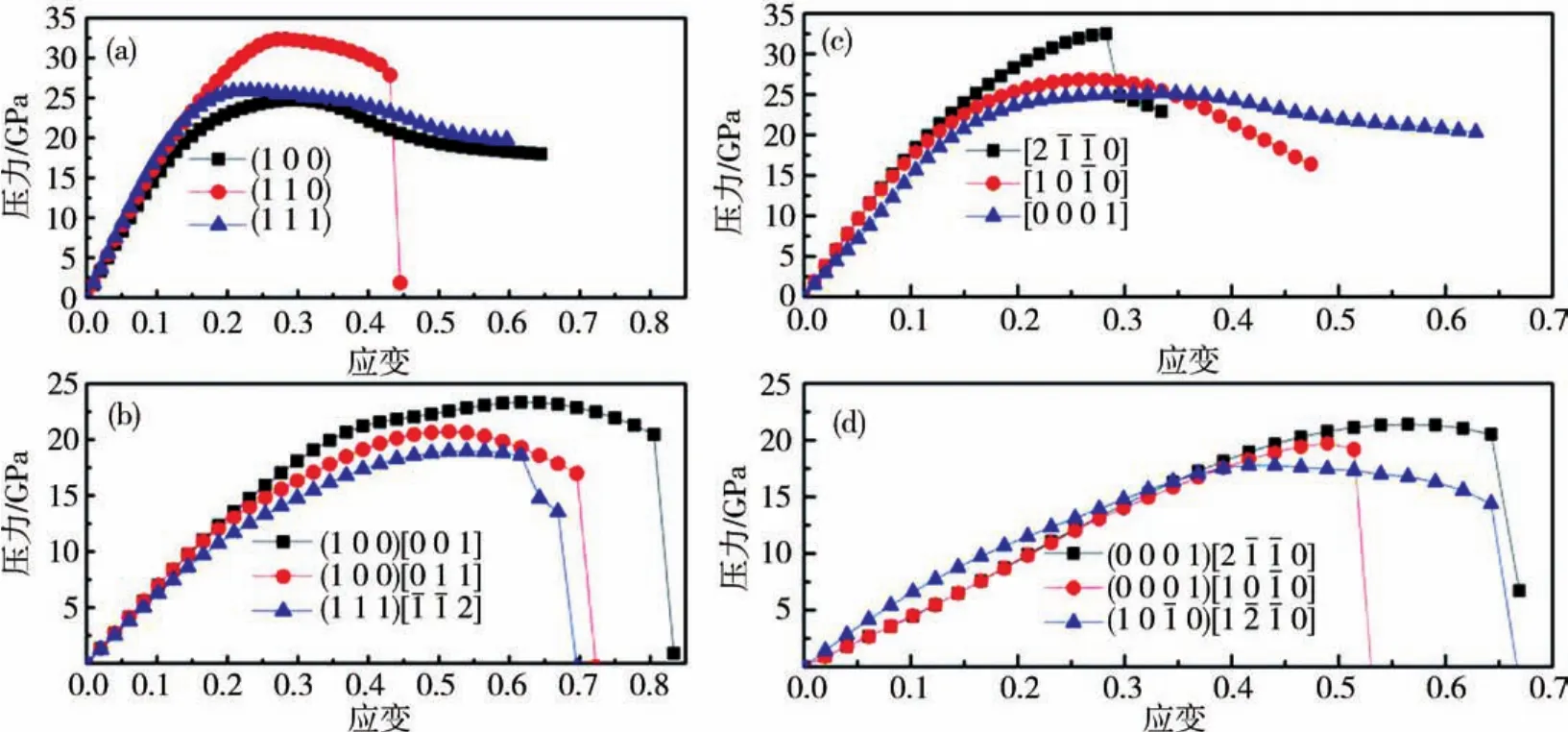
圖8 HfCr2合金立方和六角相沿各個方向的應力應變關系Fig.8 Calculated stress-strain relations of fcc phase and hcp phase in various directions for HfCr2alloy

3 結論

本文研究采用基于密度泛函理論的第一性原理平面波贗勢方法，系統地探索了HfCr2合金的立方相和六角相在0～20 GPa壓力范圍內的物理性質.具體研究內容包括合金結構穩定性、電子結構、彈性模量、各向異性、泊松比、脆性與延展性以及應力-應變曲線.對HfCr2合金2種相結構的研究表明，立方相和六角相均滿足力學穩定性要求，而從能量的角度看，立方相結構更為穩定，說明六角相為亞穩結構.對合金電子結構的分析表明，費米能級處態密度源自于Hf（Cr）原子p態和d態的貢獻，表現出一定的p-d軌道雜化行為.立方相結構費米能級處的態密度值小于六角相相應位置處的態密度值，因此立方相結構要更穩定.本文計算了2個相的彈性模量，發現在整個壓力范圍內，2個相的體模量、楊氏模量和剪切模量都隨壓力的增強而增大.計算同時表明在通常條件下，立方相顯示出較強的彈性各向同性，而六角相雖然總體上也表現出彈性各向同性，但與立方相相比則顯示出一定程度的各向異性.隨壓力的增加，立方相的彈性各向異性減弱，而六角相的彈性各向異性則增強.對體模量與剪切模量各向異性百分比的研究表明，在研究的壓力范圍內，2種相結構的體模量和剪切模量總體上都表現出較強的空間各向同性，但相對于六角相而言，立方相剪切模量表現出更強的各向同性.對彈性模量3D方向示意圖的研究也表明，0 GPa時2種結構的體模量總體上都表現出較強的各向同性，但相比于立方相的楊氏模量，六角相楊氏模量的各向異性要更強一些.在整個壓力范圍內，泊松比隨壓力增長單調增大，而G/B比值變化趨勢與此相反，二者都表明合金是延展性材料，且延展性隨壓力增大逐漸增強.應力-應變關系的研究表明，立方相結構理想的拉伸強度出現在［1 0 0］方向，其值為 24.7 GPa，而（1 1 1）［1—1—2］方向為理想剪切強度出現的方向，其值為19.0 GPa；六角相結構的理想拉伸強度出現在［0 0 0 1］方向，其值為25.2 GPa，沿著（1 0 1—0）［1—2 1—0］方向的最大剪切應力17.8 GPa為該結構下合金的理想剪切強度.