基于氣動/彈道耦合的激波針外形優化研究
單繼祥,趙 平,龔志斌,陳強洪
(中國工程物理研究院 總體工程研究所,四川 綿陽 621999)
對于以侵徹彈為代表的火箭彈,可通過提高其落地速度,以實現更優的綜合性能。因此,在氣動布局設計過程中應盡量減小氣動外形阻力。在彈體前安裝激波針是一種非常簡單、有效的超聲速減阻方法[1-3]。
激波針的減阻效果與其外形參數密切相關,國內外的相關研究主要集中在激波針的外形參數影響及其優化,包括激波針的長短、不同外形以及不同攻角時的氣動性能[4-10]。侯文新等[4]在Isinght優化平臺的基礎上,以熱流和阻力系數最小為目標,開展了激波針外形多目標優化設計。李永紅等[5]對多種外形激波針的減阻效果進行了比較,結果表明,半圓形激波針跨、超聲速減阻效果最優,但在亞聲速將增大阻力。
目前,關于激波針的優化研究主要是針對某一超聲速下特定馬赫數進行減阻優化,對其他馬赫數下的阻力特性不予考慮或設定約束。同時,不同馬赫數下激波針外形最優尺寸差異較大。但在火箭彈實際飛行過程中,馬赫數遍及低、亞、跨、超聲速,覆蓋范圍較廣,單單對某一代表性馬赫數下的外形進行優化難以實現性能最佳。
本文采用氣動/彈道耦合的優化方法,以具有頭部激波針的火箭彈為計算模型,結合試驗設計、近似模型、優化算法等技術,以落地速度最大作為優化目標,對激波針外形進行了優化設計,并對不同激波針外形阻力特性、彈道特性進行了對比研究,分析了激波針的減阻、增速機理。該研究為該類飛行器激波針的設計、優化提供了參考。
1 計算模型及彈道特性
1.1 計算模型
本文的計算模型如圖1所示。全彈采用尖拱外形頭部,旋成體彈身,“×”型尾翼。彈身半徑為200 mm,頭部尖拱段長度為300 mm。
基于增強減阻效果、降低氣動熱影響的考慮,激波針采用半球盤外形。該激波針具有半球體頭部和旋成體身部。初始激波針球頭半徑為80 mm,長度為彈身直徑的2倍,如圖1(b)所示。
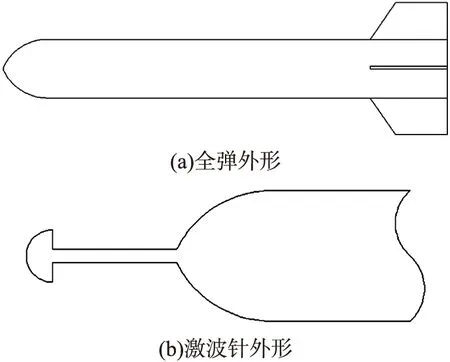
圖1 計算模型
1.2 彈道特性
本文計算時采用的彈道為理想條件下的慣性彈道。飛行過程中,全程攻角為0。無激波針時的彈道曲線如圖2所示。全彈主動段結束時的速度,即飛行過程中的最大速度約為900 m/s,然后飛行速度逐漸降低,當射程大于15 km后,其飛行速度平均在400 m/s,對應馬赫數約為1.2。飛行最大高度為16.5 km,射程為42.4 km。
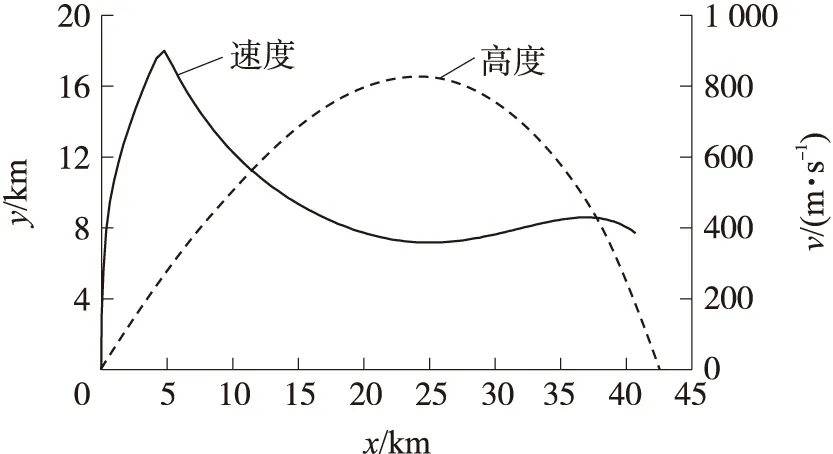
圖2 彈道曲線
2 優化方法
2.1 氣動/彈道耦合設計思路
圖3為氣動/彈道耦合設計思路與傳統設計思路的比較。
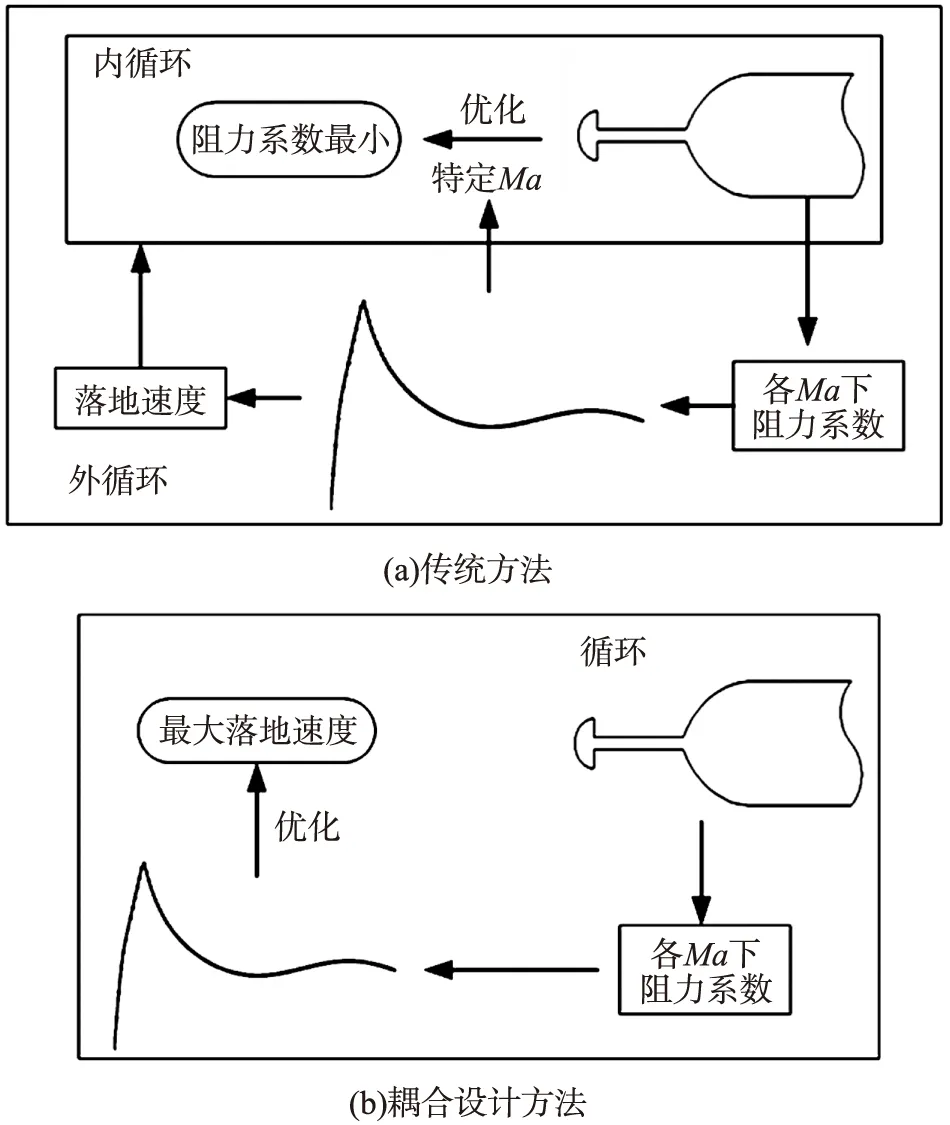
圖3 傳統設計方法與耦合設計方法的比較
傳統的激波針優化設計只針對主要飛行馬赫數開展優化,無法考慮全彈道內飛行馬赫數對氣動優化的影響。氣動/彈道耦合設計不是針對特定的彈道飛行馬赫數開展優化,而是采用數值模擬方法計算獲得某一外形全彈道典型馬赫數范圍內的阻力系數,并采用以上阻力系數開展飛行彈道計算,獲得對應外形的落地速度,即通過氣動、彈道的耦合計算獲得激波針外形參數與落地速度的直接對應關系,并以落地速度為直接優化目標開展激波針外形優化設計。
2.2 優化方法及流程
2.2.1 優化流程
不同于基于CFD的優化迭代方法,本文采用代理模型建立激波針外形參數與落地速度的預測模型,并采用遺傳算法(genetic algorithm,GA)實現滿足約束條件下的激波針外形優化,以獲得最大落地速度的激波針外形。優化流程圖如圖4所示。
如圖4所示,本文的優化步驟如下:
①利用拉丁超立方采樣法在整個計算空間抽樣獲得N個采樣點,建立設計空間里的激波針外形樣本方案;
②對N個樣本進行幾何建模,采用CFD方法計算各樣本方案典型馬赫數下的阻力系數,并通過彈道仿真獲得樣本對應的落地速度;
③用各個樣本方案的外形參數和對應的落地速度組成樣本庫,構建兩者之間的Kriging代理模型;
④分析代理模型精度,如果精度達不到要求,則回到①,增加樣本點數量,提高代理模型可信度,直到模型精度滿足要求;
⑤基于以上代理模型,以最大落地速度為優化目標,采用遺傳優化方法搜索最優激波針外形,并對該外形開展CFD計算及彈道計算,驗證落地速度。
2.2.2 Kriging代理模型
Kriging是一種使用廣義高斯方程作為基函數的特殊形式徑向基函數插值方法。該方法是根據樣本空間的位置與樣本之間的關聯程度,對不同的樣本賦予不同的權值,通過滑動加權平均,從而估計未知空間的樣本信息。
Kriging代理模型的預測響應值和均方誤差(mean square error,MSE)可以表示為
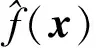
2.2.3 遺傳優化算法
遺傳優化算法是一種模擬生物學中進化理論的優化算法。遺傳優化算法首先生成初始種群,并計算種群中每個個體的適應度值,判斷是否滿足終止準則。若滿足要求,則停止計算,輸出優化最優解;若不滿足,則執行遺傳算子部分的選擇、變異、交叉操作,經過多次迭代實現種群的進化。通過遺傳優化算法可獲得全局最優解,且不依賴于初值。
2.3 數值模擬方法
全彈氣動特性的計算采用基于有限體積法的數值模擬方法,控制方程采用三維雷諾平均Navier-Stoke方程組,其形式如下:
式中:Q為守恒量;F,G,H為無黏通量;Fv,Gv,Hv為黏性通量。數值計算中的湍流模型采用k-ωSST模型。
2.4 計算方法驗證
本文對全彈氣動力的數值模擬結果和試驗結果進行了比較,以驗證數值模擬方法和網格的可靠性。
圖5是當Ma=1.9時,某模型有、無激波針時阻力系數CD的數值模擬和風洞試驗結果比較。可以看出,相同模型時零攻角阻力系數數值模擬結果與試驗結果基本一致,且各攻角時激波針減阻量的數值模擬結果和試驗結果較為吻合。采用本文的數值計算方法開展激波針優化設計是可行的。
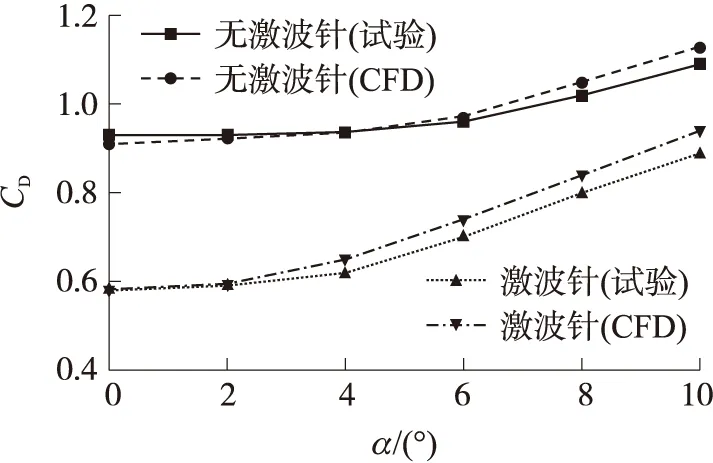
圖5 計算結果與風洞試驗結果比較(Ma=1.9)
3 優化結果與分析
3.1 不同馬赫數下激波針減阻特性
本文首先研究了亞、跨、超聲速來流條件下,球頭激波針參數對零攻角時全彈減阻效果的影響及其流動機理。
圖6、圖7分別是零攻角、不同馬赫數條件下,激波針長度、頭部半徑對減阻效果影響的曲線。圖中,rp為彈身半徑;rs為激波針半徑;l為激波針長度。
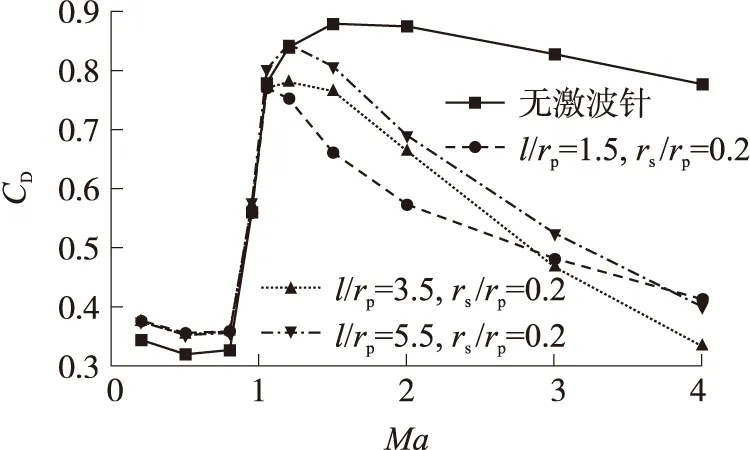
圖6 激波針長度對減阻效果的影響
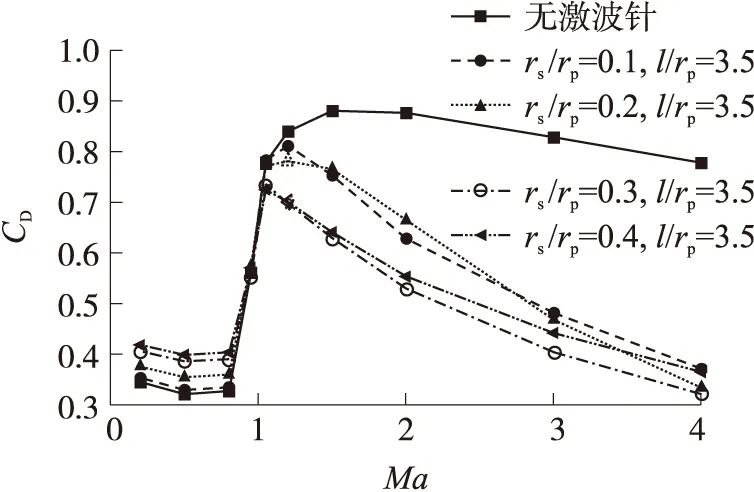
圖7 激波針頭部半徑對減阻效果的影響
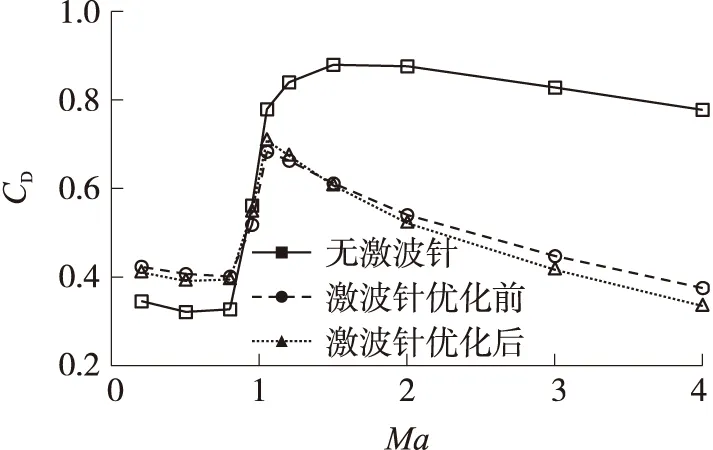
從圖中可以看出,亞聲速時,激波針的存在將導致全彈阻力增加,且阻力增量隨著球頭部半徑的增大而迅速增大,隨著激波針長度的增大基本不變。跨聲速時,部分外形時,激波針的存在將使全彈阻力減小,合理設計的激波針外形可實現跨聲速減阻,但其減阻效果并不明顯。超聲速時,各參數條件下,激波針均能起到較好的減阻效果,且隨著馬赫數的增大,相同激波針外形的減阻效果逐漸增強。同時,值得注意的是,各馬赫數下的最佳減阻外形不同,隨著馬赫數的增大,最佳激波針減阻外形的長度逐漸增大。
表1給出了典型馬赫數時激波針及彈體的阻力系數。圖8是典型馬赫數下,激波針外形對稱面頭部馬赫數云圖。
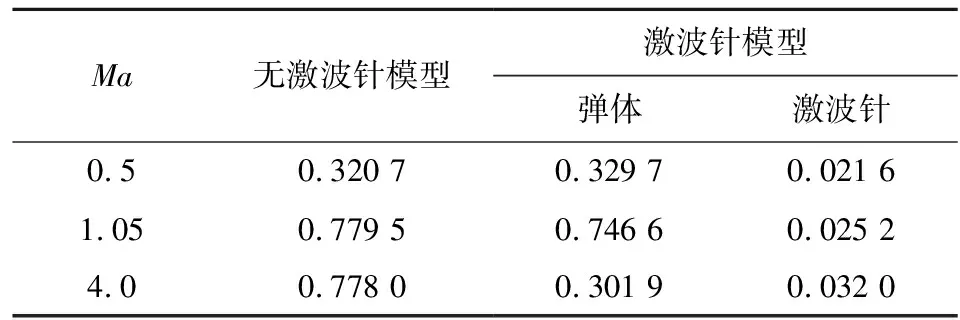
表1 典型馬赫數時激波針及彈體阻力系數

圖8 典型馬赫數下激波針附近馬赫數云圖
可以看出,各典型馬赫數下,激波針均產生了顯著的附加阻力。亞聲速時,激波針存在導致彈體阻力小幅增大,加上激波針產生的附加阻力,導致全彈阻力系數增大。跨、超聲速時,在頭部增加激波針,可消除光頭彈體頭部弓形激波,使彈體頭部波阻減小。跨聲速時,彈體阻力的減小量與激波針的附加阻力量值相當,導致激波針的減阻效果有限。隨著馬赫數的進一步增大,超聲速時彈頭波阻的減小幅度大于激波針附加阻力的增幅,從而導致全彈減阻量逐漸增大。
3.2 基于落地速度最大的激波針外形優化
針對半球形激波針外形,通過優化激波針球頭半徑rs及激波針長度l實現減阻,從而提高全彈的落地速度v。
該優化問題可歸納為
優化目標:maxv。
約束條件:射程X>42.4 km。
設計變量:球頭半徑rs∈[20 mm,80 mm],長度l∈[300 mm,1 100 mm]。
在初始優化外形方面,選取Ma=1.2時(無激波針時彈道主要飛行馬赫數)減阻效果較佳的激波針外形參數,rs=80 mm,l=460 mm。
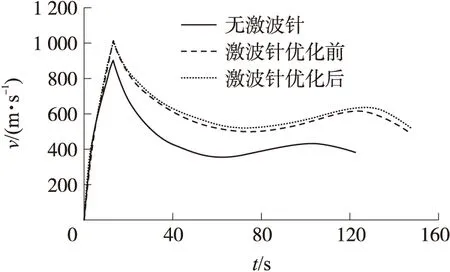
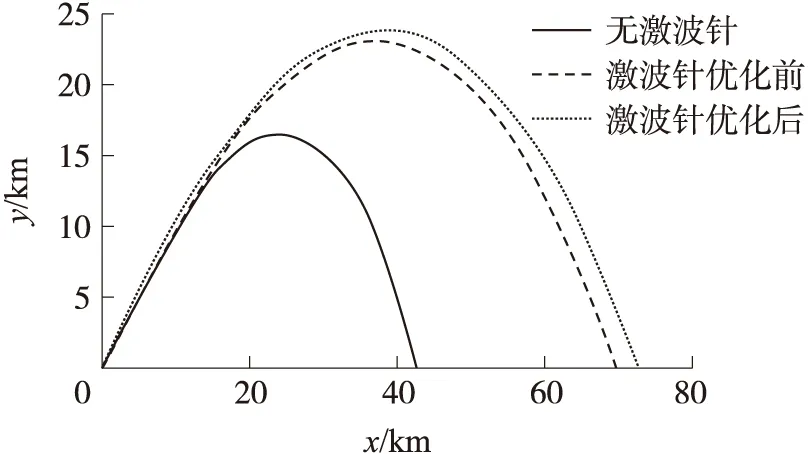
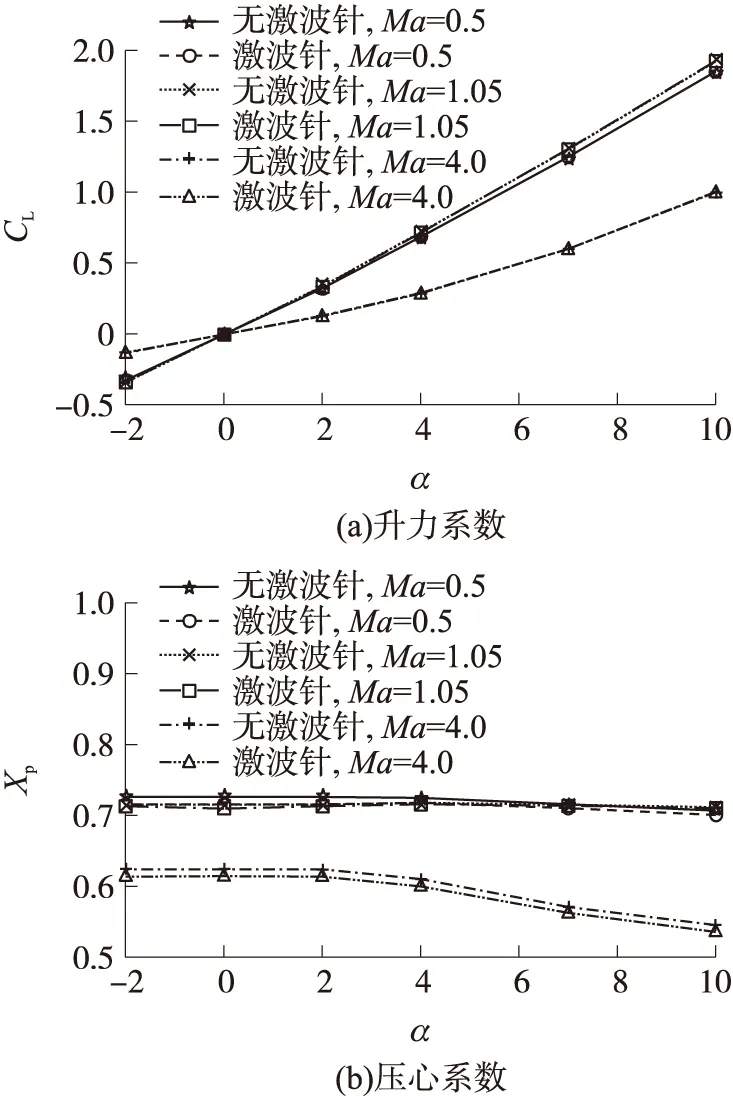
優化前后激波針外形參數如圖9所示,其各馬赫數下全彈阻力系數曲線如圖10所示。通過比較優化前后激波針外形參數,可以看出,優化后激波針長度有所增大,激波針球頭半徑則有所減小。激波針外形的以上變化將使亞聲速、超聲速時的阻力系數減小,跨聲速時(0.95≤Ma<1.5)的阻力系數增大。由優化前后激波針模型彈道飛行速度曲線的比較(如圖11所示)可以看出,與無激波針模型相比,隨著主動段(飛行馬赫數范圍為0.1 圖12是有、無激波針模型飛行彈道的比較。從中可以看出,增加頭部激波針后,全彈最大飛行高度、射程均大幅增加,提高了該彈的打擊范圍。與無激波針模型相比,優化后激波針模型最大高度由16.5 km提高到23.7 km左右,射程由42.4 km增大到72.3 km,提高了70.0%。與優化前激波針模型相比,優化后激波針模型射程進一步提高,使激波針對射程的改善效果進一步提高10.0%。這說明激波針優化對射程能力也有提高作用。 圖9 激波針優化前后外形示意圖 圖10 優化前后激波針模型阻力系數比較 圖11 有、無激波針模型飛行速度比較 圖12 有、無激波針模型飛行彈道比較 對于以慣性彈道飛行(零攻角)的無控彈,要求全彈有較高的靜穩定裕度,以減弱風干擾、推力偏心等干擾對落點精度的影響。 圖13是典型馬赫數下,有、無激波針模型全彈升力系數、壓力系數隨攻角的變化曲線。可以看出,與無激波針外形相比,優化后激波針模型升力系數CL、壓心系數Xp均變化較小。當Ma=4.0時,激波針對縱向氣動力影響最大,最大可使升力系數增加0.8%左右,壓心系數前移1%。總體而言,增加激波針對全彈升力特性、靜穩定特性均影響較小。 圖13 典型馬赫數下有、無激波針時全彈氣動力比較 本文采用數值模擬方法研究了亞跨超聲速范圍內球頭激波針外形參數對減阻效果的影響及其流動機理,并以最大落地速度為優化目標,基于氣動/彈道耦合優化方法對激波針外形進行了優化。結果表明: ①亞、跨聲速范圍內,由于激波針產生的附加阻力較大, 使得全彈阻力系數增大, 激波針無減阻效果;超聲速時,激波針的減阻效果明顯,且隨馬赫數的增大,最佳減阻外形的長度增大,半徑減小; ②基于氣動/彈道耦合的激波針外形優化方法充分考慮了氣動、彈道間的相互影響,優化后可使落地速度、射程在基礎上進一步提高10.0%左右; ③亞、跨聲速范圍內,增加激波針對全彈升力特性、靜穩定特性均影響較小。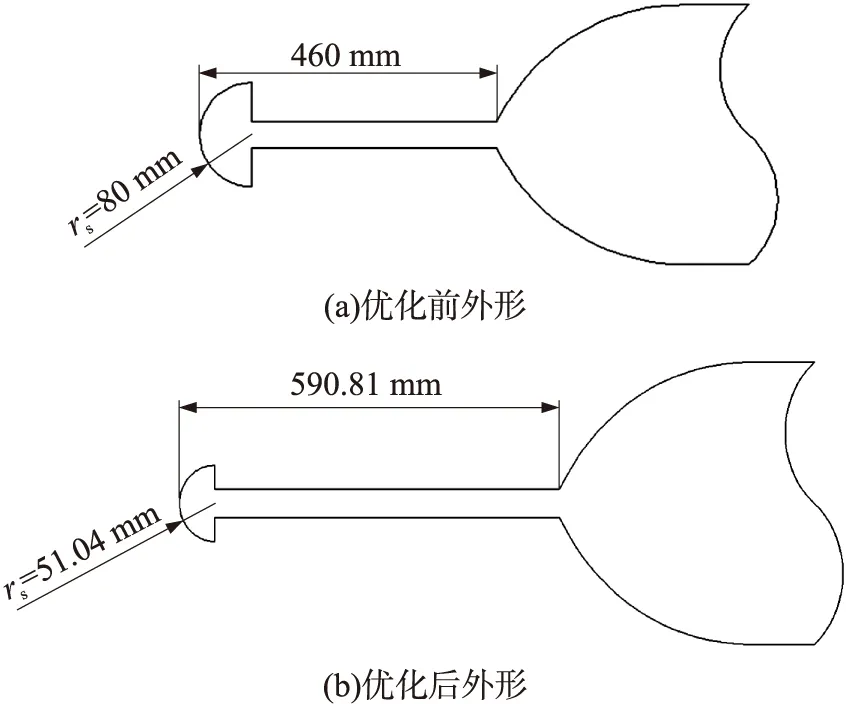
3.3 頭部激波針對全彈氣動特性的影響
4 結論

