高效可撤銷的身份基在線離線加密方案

王占君，馬海英，王金華，李 燕

1.南通大學 理學院，江蘇 南通 226019

2.南通大學 信息科學技術學院，江蘇 南通 226019

1 引言

1984 年，Shamir 首次提出了身份基加密（Identity-Based Encryption，IBE）[1]的概念。在IBE 中，用戶可以使用一個字符串（例如，家庭住址、身份證號、email地址等）表示自己的身份信息，密鑰生成中心（Key Generation Center，KGC）利用該身份信息和系統(tǒng)主密鑰為其生成用戶私鑰，加密者利用接收者身份信息和系統(tǒng)公鑰加密消息。IBE 刪除了傳統(tǒng)公鑰加密機制中證書驗證過程，提高了加密效率。隨后，學者們提出了許多實用的IBE 方案[2-4]，然而，在實際應用，用戶私鑰可能會泄漏、丟失或者到期，因此，IBE需要提供一種有效的成員私鑰撤銷機制。

針對IBE的成員撤銷問題，現(xiàn)有的解決方案利用完全子樹和子集不同方法可以實現(xiàn)成員撤銷[5]。由于利用完全子樹撤銷方法，用戶僅需存儲較短的私鑰，Boldyreva等人[6]基于該方法提出了成員撤銷的IBE方案。該IBE方案利用用戶身份和時間進行加密，KGC 根據(jù)最新成員撤銷列表，周期性地發(fā)布未撤銷用戶的更新鑰，使得未撤銷用戶利用相應的更新鑰可以重構自己的解密鑰。由于更新鑰的工作量過大，導致KGC 可能構成系統(tǒng)的瓶頸。該方案[6]僅滿足選擇身份模型下的安全性。為了提高系統(tǒng)的安全性，文獻[7]提出適應性安全的可撤銷IBE 方案，文獻[8-10]在此基礎上進一步增強系統(tǒng)安全，提出了抗密鑰暴露攻擊的可撤銷IBE 方案。然而，加密過程需要執(zhí)行一些橢圓曲線上的冪乘運算，很難適用于輕量級設備。

為了提高 IBE 中的加密效率，2008 年，Guo 等人提出了身份基在線離線加密方案[11]，將加密過程分解為離線和在線兩個階段，離線階段首先對大部分加密運算進行預處理生成離線密文，在線階段利用離線密文執(zhí)行少量簡單運算生成密文，提高了實際加密的效率。隨后，研究人員提出了一系列高效的身份基在線離線加密方案[12-16]和屬性基在線離線加密方案[17-18]。然而，現(xiàn)有的身份基在線離線加密方案都不能實現(xiàn)用戶撤銷的功能。

本文提出了一種高效的可撤銷成員的身份基在線離線加密。利用完全子樹方法實現(xiàn)用戶的撤銷，首先，生成一顆完全二叉樹，每個節(jié)點指定一個一次多項式f(x)=ax+1，利用該多項式將1 分解成兩個份額f(1)和f(T)，其中，T為時間且大于1，利用份額f(1)來生成用戶的身份私鑰，利用f(T)來生成用戶的更新鑰。密鑰生成中心周期性的發(fā)布更新鑰，任意非撤銷用戶可以重構自己的解密鑰。由于所有撤銷用戶都擁有相同的份額f(1)，其聯(lián)合起來也不能重構解密鑰，從而該方案可以抵抗聯(lián)合攻擊。為了減輕輕量級設備加密的負擔，利用在線離線技術，將加密過程分解為離線階段和在線階段。在得知消息和接受者身份前，離線階段執(zhí)行大部分的加密工作。一旦得知消息和接受者身份之后，輕量級設備利用離線密文經(jīng)過少量簡單運算即可快速生成密文。特別地，離線階段可在空閑時間利用高性能計算機執(zhí)行。與相關知名方案相比，本文方案不僅提高了KGC 生成更新鑰的效率，而且極大地減輕了輕量級設備的加密負擔。

2 雙線性對和DBDHI假設

雙線性對：設G和GT都是素數(shù)p階的循環(huán)群，g是群G的生成元，e:G×G→GT是一個映射，且滿足：（1）雙線性，對?u,v∈G,β,δ∈Z，則e(uδ,vβ)=e(u,v)δβ；（2）非退化性，e(g,g)≠1；（3）可計算性：對 ?u,v∈G，可在多項式時間內(nèi)計算e(u,v)，則稱e為一個雙線性對。

2(l+1)-DBDHI 假設：設g是群G的生成元，x∈，給定一個2(l+2)元組，則任意多項式時間算法A判定T=e(g,g)1/x或T是GT中的隨機元素的優(yōu)勢都是可以忽略的。

3 RIBOOE定義和安全模型

一個可撤銷成員的身份基在線離線加密（RIBO0E）方案由初始化（Setup）、私鑰生成（Genkey）、更新鑰生成（Updatekey）、解密鑰生成（Derivekey）、離線加密(Encoff)、在線加密 (Encon)、解密（Dec）、撤銷（Revoke）算法構成。

Setup（λ，Nmax）→PP,MK,RL,ST。KGC 運行初始化算法，輸入安全參數(shù)λ和用戶最大個數(shù)Nmax，輸出系統(tǒng)主密鑰MK，公共參數(shù)PP，撤銷列表RL，狀態(tài)ST。

Genkey(ID,MK,ST,PP)→SKID，ST′。KGC運行私鑰生成算法，輸入身份ID、管理員密鑰MK，狀態(tài)ST和公共參數(shù)PP，輸出ID的私鑰SKID和更新的狀態(tài)ST′。

Updatekey(T,PP,MK,RL,ST)→UKT,R。KGC運行更新鑰生成算法，輸入時間T、公共叁數(shù)PP、系統(tǒng)主密鑰MK、撤銷列表RL狀和態(tài)ST，輸出T時刻的更新鑰UKT,R其中R為T時刻的撤銷身份集合。

Derivekey (SKID,UKT,R,PP)→DKID,T/⊥。用戶運行解密鑰生成算法，輸入私鑰SKID，更新鑰UKT,R和公共參數(shù)PP，輸出解密密鑰DKID,T或失敗符號⊥。

Encoff(PP)→CToff。用戶可以利用高性能設備在空閑時間運行離線加密算法，輸入公共參數(shù)PP，輸出離線密文CToff。

Encon(PP,ID,T,M,CToff)→CTID,T。用戶利用輕量級設備運行在線加密算法，輸入公共參數(shù)PP、身份ID、時間T、消息M和離線密文CToff，輸出密文CTID,T。

Dec (CTID,T,DKID',T',PP)→M/⊥。接收者運行解密算法，輸入密文CTID,T、解密鑰DKID',T'和公共參數(shù)PP，當ID=ID′且T=T′時，輸出消息M，否則輸出失敗符號⊥。

Revoke(ID,T,RL,ST)→RL′。KGC 運行撤銷算法，輸入身份ID、時間T、撤銷列表RL和狀態(tài)ST，輸出更新后的撤銷列表RL′。

RIBOOE的安全性由攻擊者A和挑戰(zhàn)者C之間的游戲來定義如下。

開始：A提交挑戰(zhàn)身份ID*、挑戰(zhàn)時間T*、T*時刻的撤銷列表RL*給挑戰(zhàn)者C。

初始化：挑戰(zhàn)者C運行Setup算法，生成系統(tǒng)主密鑰MK、撤銷列表RL、狀態(tài)ST、公共參數(shù)PP，并將PP發(fā)送給敵手A。

階段1 敵手A可以適應性地詢問如下3個預言機。

（1）私鑰生成預言機OSK（·），敵手A 提交身份ID給C，C 運行Genkey(ID,MK,ST,PP)算法，返回SKID給A。

（2）更新鑰生成預言機OUK（·），敵手A 提交時間T給C，C運行Updatekey(T,PP,MK,RL,ST)算法，返回UKT,R給A。

（3）撤銷預言機ORev（·，·），敵手A提交身份ID和時間T給C，C 運行Revoke(ID,T,RL,ST)算法，并返回新的撤銷列表RL′給A。如果敵手A 詢問過，則C必須在T*時刻之前撤銷掉用戶ID*。

挑戰(zhàn)：敵手A提交兩個長度相等的消息M0，M1給C，C隨機選擇μ∈{0,1}，運行Encon(PP,ID,T,M,CToff)并將，返回給A。

階段2 與Phase1相同。

猜測：A輸出μ的猜測值μ′，如果μ′=μ，則稱A贏得該安全性游戲。

敵手A的優(yōu)勢AdvRIBOOE=|Pr[μ=μ′]-1/2|。如果任意多項式時間敵手A 贏得上述游戲的優(yōu)勢都是可以忽略的，則稱RIBOOE 在選擇撤銷身份列表（Selective-Revocation-List）模型下是安全的。

4 RIBOOE方案

本文方案利用完全子樹方法撤銷用戶。首先生成一棵完全二叉樹，每個節(jié)點指定一個一次多項式f(x)，使得f(0)=1。每個用戶被指定到一個葉子節(jié)點，獲得從其葉子節(jié)點到根節(jié)點路徑上每個節(jié)點處的身份私鑰。利用X=e(g,g)s加密消息。給定T時刻的撤銷用戶集合R，KGC生成非撤銷用戶的覆蓋集合，為覆蓋集合中的每個節(jié)點生成更新鑰，使得未撤銷用戶利用更新鑰可以計算Xf(T)，利用身份私鑰計算Xf(1)，由于f(x)為一次函數(shù)，利用Xf(T)和Xf(1)可以算出Xf(0)，可以成功解密密文。特別地，撤銷用戶僅能計算Xf(1)，即使任意多個撤銷用戶聯(lián)合起來也得不到f(x)上的其他點，不能重構函數(shù)f(x)，所以，無法獲知f(0)的值，導致撤銷用戶解密失敗。因此，本文方案滿足抗聯(lián)合攻擊性。

Setup(λ,Nmax)：該算法輸入安全參數(shù)λ和用戶最大個數(shù)Nmax，生成素數(shù)p階的雙線性群e:G×G→GT，令g為G的生成元。隨機選擇，計算，，生成存放(ID,u)的用戶列表UL，存放(u,fu(x))的函數(shù)列表FL。設M為消息空間，|M|=nM，選擇Hash 函數(shù)，然后，生成一棵完全二叉樹BT，使其至少有Nmax個葉子節(jié)點。對該樹的任意葉子節(jié)點u，隨機選擇一個一次函數(shù)fu(x)，使得fu(0)=1，并存放(u,fu(x))到FL。最后，輸出系統(tǒng)主密鑰MK=(y1,y2,FL)、撤銷用戶列表RL、狀態(tài)ST=(BT,UL) 和公共參數(shù)PP=(g,Y1,Y2,e(g,g),H1,H2)。

Genkey(ID,MK,ST,PP)：該算法輸入身份ID、系統(tǒng)主密鑰MK，狀態(tài)ST和公共參數(shù)PP。首先，選擇一個未使用的葉子節(jié)點u，將ID指定給葉子節(jié)點u，并保存該元組(ID,u)到UL中。然后，對于任意節(jié)點z∈Path(u)，檢索函數(shù)列表FL={(u,fu(x))|?u∈BT}，計算：

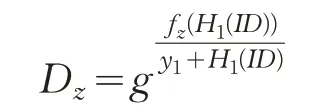
最后，輸出更新的狀態(tài)ST和用戶私鑰SKID={Path(u),。

Updatekey(T,PP,MK,RL,ST)：該算法輸入時間T、公共叁數(shù)PP、系統(tǒng)主密鑰MK、撤銷列表RL和狀態(tài)ST。首先利用RL定義T時間的撤銷用戶集合R，即如果存在 (ID′,T′)∈RL且T′≤T，則ID′∈R，根據(jù)用戶列表UL定義撤銷集合索引RI，得到撤銷用戶的覆蓋集合CVRI。然后，對任意z∈CVRI，計算：

最后，輸出更新的狀態(tài)和更新鑰UKT,R={CVRI,{Ez}z∈CVRI}。

DeriveKey(SKID,UKT,R,PP)：該算法輸入SKID={Path(u),{Dz}z∈Path(u)} ，UKT,R={CVRI,{Ez}z∈CVRI} ，如果ID?R，由完全子樹方法得z∈Path(u)∩CVRI，得到解密鑰：

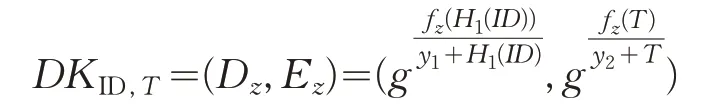
否則輸出⊥。

Encoff(PP) ：該算法輸入公共參數(shù)PP，隨機選擇s,δ,β∈Zp，計算R=e(g,g)s，R0=H2(R)，R1=(Y1gδ)ss，R2=(Y2gδ)s，輸出離線密文CToff=(R0,R1,R2,s,δ,β)。

Encon(PP,ID,T,M,CToff)：該算法輸入公共參數(shù)PP、身份ID、時間T、消息M和離線密文CToff，計算C=R0⊕M,C1=s(H1(ID)-δ)，C2=s(T-β)，輸出密文CTID,T=(C,C1,C2,R1,R2)

Dec(CTID,T,DKID',T',PP)該算法輸入密文CTID,T，解密鑰DKID',T'和公共參數(shù)PP，當ID=ID′且T=T′時，則計算：

輸出明文M=H2(e(g,g)s)。

Revoke(ID,T,RL,ST)：該算法輸入身份ID、時間T、撤銷列表RL、狀態(tài)ST=(T,UL)，如果(ID,*)∈UL，輸出⊥；否則將(ID,T)加入到RL中，輸出更新后的撤銷列表RL′。

5 安全性證明

定理如果2(l+1)-DBDHI假設成立，則本文RIBOOE方案在選擇撤銷身份列表模型下是安全的。

證明假定存在一個敵手A 能攻破RIBOOE 方案，則可以構造一個算法B攻破2(l+1)-DBDHI假設。

開始：A 提交挑戰(zhàn)身份ID*、挑戰(zhàn)時間T*和T*時刻的挑戰(zhàn)撤銷列表RL*。

（1）?z∈FixedSubset(ID*)，隨機選擇y∈Zp，隱式的保存(x=H1(ID*),αy)到FL；

（2）?z?FixedSubset(ID*)，隨機選擇y∈Zp，隱式的保存(x=H1(T*),αy)到FL，注意一次函數(shù)fu(x)被兩個點（0，1）和(x,αy)所確定。

B設置撤銷列表RL和狀態(tài)ST=(BT,UL)，隨機選擇π1，π2∈{1,2,…,l}，Iπ1，w1,w2,…,wπ1-1,wπ1+1,…,wl∈Zp，當i≠π1時定義，對系統(tǒng)運行時間T1,…,…,Tl，計算 2(l-1) 次多項式：

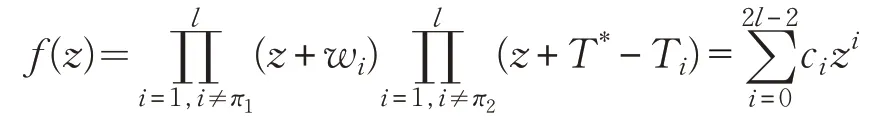
構造生成元：

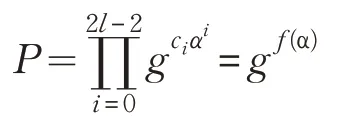
當i{1,…,l}{π1}時，B計算：

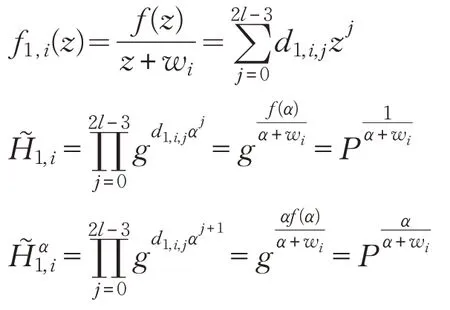
當i∈{1,…,l}{π2}時，B計算：

階段1 A 適應性的進行哈希函數(shù)隨機預言機、私鑰、更新鑰詢問。

針對哈希函數(shù)H1的詢問，假設第v次詢問的身份為IDv，B設置H1(IDv)=Iv。

針對身份IDi的私鑰詢問，當IDi≠ID*時，首先構造點（0，1）的臨時鑰部件：

若(IDi,*)∈UL，從UL中下載(IDi,u)，否則隨機選擇u使得u≠u*∧(*,u)?UL，并保存(IDi,u)到UL，然后得到Pathu。對節(jié)點z∈Pathu，檢索函數(shù)列表(u,fu(x))，若z∈FixedSubset(ID*)，此時(x=H1(ID*,αy)：

若z?FixedSubset(ID*)，此時 (x=T*,αy)：

當IDi=ID*時，此時必有ID*∈R*，從UL中下載(ID*,u*)，得到。對，此時(x=H1(ID*),αy)：

如果敵手A 進行時間Ti的更新鑰詢問，當Ti≠T*時，構造點（0，1）的臨時鑰部件：

定義Ti時刻的撤銷用戶集合R，并得到覆蓋集合CVRI，對節(jié)點z∈CVRI，檢索函數(shù)列表 (u,fu(x))。若z∈FixedSubset(ID*)，此時 (x=H1(ID*),αy)：

若z?FixedSubset(ID*)，此時 (x=T*,αy)：

當Ti=T*時，定義T*時刻的撤銷用戶集合R*，并得到覆蓋集合CVRI*。當ID*∈R*，F(xiàn)ixedSubset(ID*)={Path(u*)}，CVRI*∩FixedSubset(ID*)=? ，當ID*?R*，F(xiàn)ixedSubset(ID*)=? ，CVRI*?FixedSubset(ID*)=? ，總之CVRI*?FixedSubset(ID*)=?。對節(jié)點z∈CVRI*，檢索函數(shù)列表(u,fu(x))。由z?FixedSubset(ID*)，注意此時 (x=T*,αy)，計算：

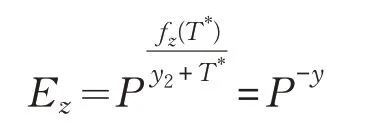
構造更新鑰為UKT,R=(CVRI,{Ez}z∈CVRI)。

挑戰(zhàn)：A 提交兩個消息M0、M1，B 隨機選擇μ∈{0,1}，d,m∈Zp，構造挑戰(zhàn)密文為：B隱式的設置s=1/α，δ=H1(ID*)+α(d+1),β=T*+α(m+1)：

當Z=e(P,P)1/α時 ，C=Mμe(P,P)s，C1,C2,R1,R2為Mμ的密文，當Z∈GT時，C,C1,C2,R1,R2為隨機消息的密文。

猜測：A 輸出猜測值μ′∈{0,1}。當μ′=μ時，B 輸出1，否則B輸出0。

6 性能比較和實驗分析

如表1 將本文RIBOOE 方案和兩個相關方案在效率和功能方面進行了比較，其中，假設素數(shù)p階的雙線性群e:G×G→GT中，E表示群G中的冪乘運算，mc表示Zp中的模乘運算，r表示撤銷用戶的個數(shù)，Nmax表示用戶最大個數(shù)。特別地，群G中冪乘的計算量遠遠大于Zp中模乘運算的計算量。

表1 本文方案與3個知名方案的性能比較

由表 1 可知，本文方案與 BGK 方案[6]和 JK[8]都能實現(xiàn)用戶撤銷，但BGK 的加密過程需要執(zhí)行橢圓曲線上的12 個冪乘運算，輕量級設備難以在短時間內(nèi)完成加密任務，且需要消耗大量電能。本文方案將加密分解成離線和在線兩個階段，加密者可以利用高性能計算機在可信環(huán)境下執(zhí)行離線加密，輕量級設備僅需執(zhí)行整數(shù)環(huán)上的兩個模乘運算即可生成密文，整數(shù)環(huán)上的模乘運算量遠遠小于橢圓曲線上的冪乘運算量。因此，與BGK方案和JK 方案相比，輕量級設備運行本文方案的加密算法效率得到了極大地提高。此外，本文方案的KGC私鑰更新工作量是BGK的1/7，是JK[8]的1/3。

WMW[15]提出了一種高效的可外包解密的身份基在線離線加密方案，該方案支持輕量級設備快速加密數(shù)據(jù)，但不能實現(xiàn)用戶撤銷的功能。與WMW[15]方案相比，本文方案支持用戶撤銷功能，盡管在線加密工作量比WMW[15]方案多執(zhí)行一個整數(shù)環(huán)上的模乘運算，由于整數(shù)環(huán)上的模乘運算量極小，輕量級設備完全能夠承擔。性能比較表明，本文方案不僅大大提高了輕量級設備的加密效率，而且極大地減少了KGC 私鑰更新的工作量，適合于輕量級設備保護用戶隱私信息。

7 結束語

本文提出高效可撤銷的身份基在線離線加密方案，該方案利用完全子樹方法實現(xiàn)用戶撤銷功能，利用在線離線技術提高輕量級設備加密效率。基于DBDHI 假設，證明本文方案是安全的。本文方案的優(yōu)勢主要表現(xiàn)在三個方面：（1）輕量級設備的加密效率很高；（2）KGC的私鑰更新工作量大大減少；（3）實現(xiàn)成員撤銷功能。因此，本文方案非常適合于移動環(huán)境中輕量級設備保護用戶隱私信息。