基于平板電極的半球諧振陀螺全角技術研究

蔣春橋, 江 黎，譚品恒，方海斌，卜繼軍

中國電子科技集團公司第二十六研究所, 重慶 400060)

0 引言

半球諧振陀螺(以下簡稱：半球陀螺)是一種固態哥氏振動陀螺，具有結構簡單、可靠性高等特點。在20世紀80年代，以美國Litton公司的產品為代表的半球陀螺在宇航領域得到成功應用。這種工作在力平衡模式(速率模式)下的半球陀螺具有高精度的優點，但測量范圍有限，帶寬較低，限制了其更廣泛的應用。近年來，法國Sagem公司研制的工作在全角模式(速率積分模式)下的半球陀螺，以其高動態、大帶寬、比例因子穩定等特點，而被廣泛用于戰術武器、艦船等領域。

國內半球陀螺的研究工作始于20世紀80年代，研制的半球陀螺工作在力平衡模式下，相應產品已成功應用于宇航領域[1]，在導彈領域的應用尚處于研究階段[2]。近年來，國內一些研究單位也開始了半球陀螺的全角模式研究，尚處于起步階段。本文對半球陀螺全角工作模式的振型控制和信號解算方法進行了研究。使用8個電極，采用時分復用的方式完成了全角模式振型控制和信號解算，并在FPGA+DSP的系統上進行了實現。實驗結果表明，兩件套半球陀螺樣機的測量范圍達±400 (°)/s，陀螺最大系統漂移為20 (°)/h。

1 半球陀螺敏感器件

半球陀螺敏感器件由半球型諧振子和平板電極組成，如圖1所示。諧振子和平板電極均由具有高品質因數(Q)值的石英材料通過精密磨削加工成型，并在表面進行金屬化處理。在平板電極上切割形成等角度分布的8個電極，用于諧振子的驅動和檢測。諧振子和平板電極通過精密微組裝工藝裝配在一起，保持諧振子唇口平面與平板電極間微小的間隙，由此形成平面電容，通過在諧振子和電極之間施加不同的電壓形成靜電力驅動諧振子振動。通過檢測諧振子與電極之間的間隙電容變化來表征諧振子的微振動。裝配好的諧振子和平板電極真空封裝在金屬殼體中，以隔離空氣阻尼的影響，保持諧振子的高Q值特性。

圖1 敏感器件實物圖

2 半球陀螺全角模式原理

當諧振子工作在四波腹模態時，假設外界旋轉角度為θ，在慣性力的作用下，諧振子的駐波與平板電極的相對位置會反向旋轉αθ。其中α為半球陀螺的進動因子，該進動因子與諧振子的結構形式有關。當結構形式為理想半球形時，α≈0.277 1。

理想諧振子的振動方程[3]為

(1)

(2)

與二維彈簧振子的傳遞函數一致，可用二維彈簧的簡化模型對球殼的振動進行分析，如圖2所示。

圖2 二維彈簧簡化模型

圖2(b)中坐標x和y分別代表0°激勵電極和45°檢測電極的位置，因此，諧振子的振動方程可簡化[4]為

(3)

(4)

式中：m為等效質量；c為等效阻尼；Ω為輸入角速率；f為外界驅動振子振動的力；Δmc、Δms表示質量分布不均勻；Δcc、Δcs表示阻尼分布不均勻；Δkc、Δks表示剛度分布不均勻。

要使質量分布不均勻和剛度分布不均勻不影響解算出的角度，q必須控制到0[5]，令

f=-2maω0[(CrI+CqJ)cosφ+(CaI+

(5)

得到陀螺的傳遞函數：

(6)

(7)

3 振型參數解算與振型控制

3.1 振型參數解算

兩路互成45°的電極的檢測信號[6]可表示為

x=acos 2θcosωτ-qsin 2θsinωτ

(8)

y=asin 2θcosωτ+qcos 2θsinωτ

(9)

解算振型參數時，在本地產生參考信號分別為

vrs=2sin(ωτ+δφ)

(10)

vrc=2cos(ωτ+(δφ)

(11)

用vrc、vrs分別與兩路檢測信號相乘并通過低通濾波器，濾除2倍頻信號并完成計算，得到：

cx=vrcx=acos 2θcosδφ-qsin 2θsinδφ

(12)

sx=vrsx=acos 2θsinδφ-qsin 2θcosδφ

(13)

cy=vrcy=asin 2θcosδφ-qcos 2θsinδφ

(14)

sy=vrsy=asin 2θsinδφ+qcos 2θcosδφ

(15)

(16)

S=2(cxcy+sxsy)=(a2-q2)sin 4θ

(17)

Li=2(cxsx+cysy)=(a2-q2)sin 2δφ

(18)

Q=2(cxsy+cysx)=2aq

(19)

(20)

得到駐波方位角、主振動幅度、正交振動幅度、相位誤差：

(21)

(22)

(23)

(24)

3.2 振型控制

由于全角模式下駐波在360°內自由進動，因此需要在360°內補充諧振子振動的能量，同時抑制正交振動。平板電極上的電極是等角度分離的8個電極，需要使用獨立電極施力的合力對諧振子的振型進行控制，其施力如圖3所示，同理可以施力抑制正交振動。

圖3 施力分解示意圖

4 全角模式振型控制實現與測試

全角模式振型控制電路采用FPGA+DSP的構架實現，其原理框圖如圖4所示。

圖4 硬件系統原理框圖

在FPGA內部完成解調、參考信號生成、控制信號合成，在DSP內部完成信號解算和PI控制信號生成。FPGA選用Xlinx公司的xc6slx45，DSP選用TI公司的TMS320F28335，搭建的陀螺系統如圖5所示。為了降低驅動信號對讀出信號的干擾，采用讀出和驅動分時復用的方法，對驅動信號進行隔離，檢測信號波形如圖6所示。為了驗證所設計的全角模式下半球陀螺的輸出有效性，搭建測試平臺對陀螺進行了角度/角速度試驗。

圖5 硬件實物圖

圖6 分時復用檢測信號波形

在1 (°)/s的轉速下，分別使陀螺旋轉0°、±30°、±45°和±90°，記錄測試數據并對其進行數據處理，如表1所示。對表中的數據用直線函數擬合，得到的比例因子為0.279 4，與理論計算值基本相符，線性度為0.001 4。經分析，線性度較差的原因是陀螺系統存在漂移，導致旋轉時間越長，系統漂移對解算角度輸出的影響越大。

表1 陀螺轉動角度和解算角度

分別在±0.1 (°)/s，±1 (°)/s，±5 (°)/s，±10 (°)/s，±50 (°)/s，±100 (°)/s，±200 (°)/s，±400 (°)/s條件下，測試了全角模式半球陀螺的線性度，如圖7所示，標度因子為0.275 3，角速率線性度為144×10-6。經分析，引起線性度不理想的因素仍是陀螺系統存在漂移；在0.001 (°)/s的條件下，測試了半球諧振陀螺的閾值，其數據如表2所示，半球諧振陀螺的閾值小于0.001 (°)/s。

圖7 陀螺角速度輸出數據及其線性擬合曲線

輸入角速率/[(°)·s-1]解算角速率/[(°)·s-1]-0.001-0.003 230-0.002 130.001-0.001 12

對半球陀螺進行長期靜態測試，讓陀螺敏感軸向指向東，陀螺輸入角速率為0，得到駐波角度曲線如圖8所示。由圖可見，駐波在不同角度下的系統漂移不一致，計入標度因子0.275 3，陀螺指向角度漂移最大值約為6.5 (°)/h。

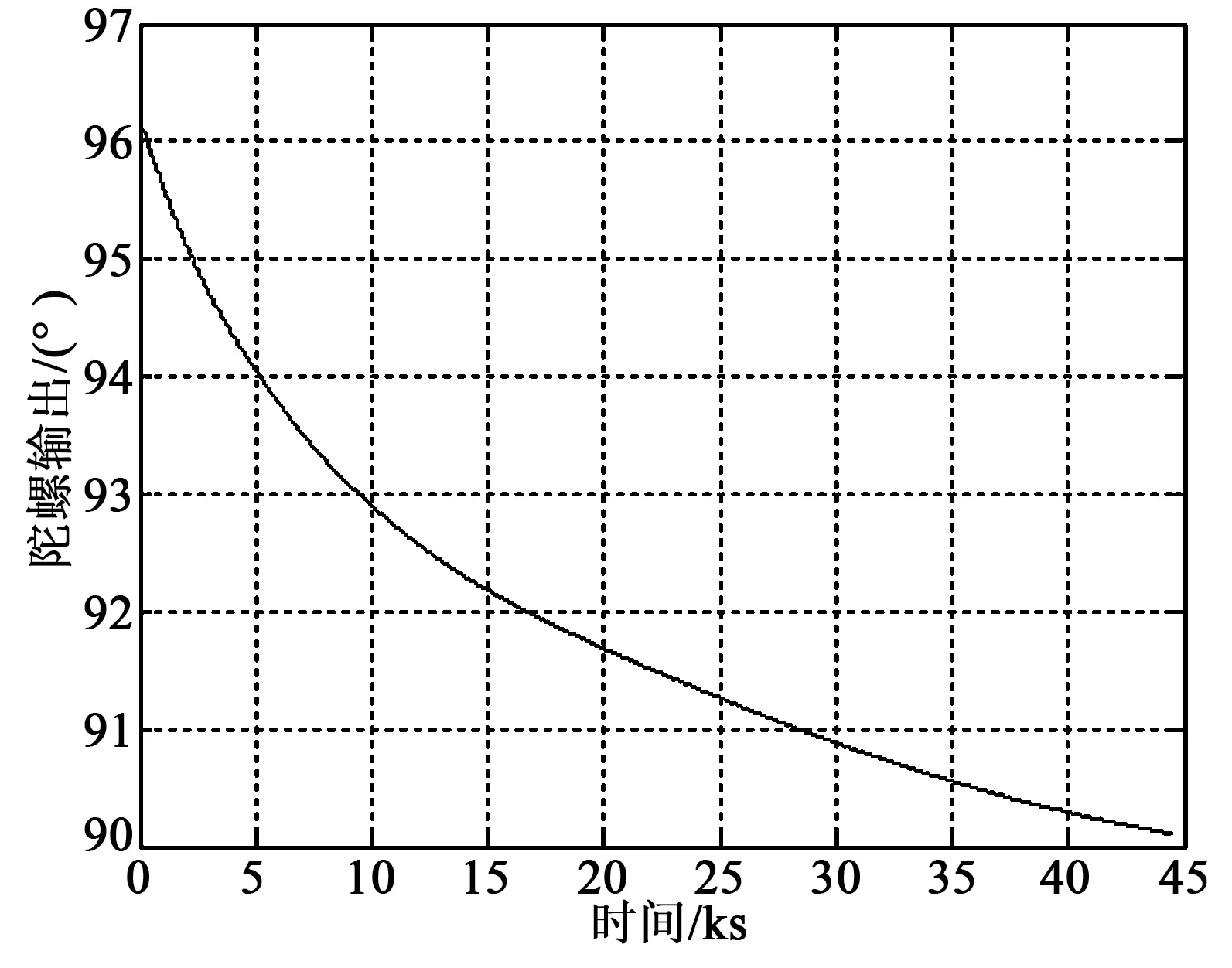
圖8 半球諧振陀螺長時漂移測試

為了獲取駐波的最大進動角速率，測試了低速轉動下陀螺的輸出曲線。當轉臺輸入0.1 (°)/s時，測試駐波位置在0°～90°進動時對應的角速率，如圖9所示。由圖可見，陀螺的角速率輸出以90°為周期成正弦分布，且重復性很好，正弦波的峰值約為20 (°)/h，即陀螺的最大系統漂移為20 (°)/h。

圖9 半球陀螺系統漂移測試曲線

5 結束語

本文對半球陀螺全角模式進行了研究，介紹了全角模式下半球陀螺的振型解算與驅動，并完成了兩件套半球陀螺樣機的全角模式系統實現。該系統完成了半球陀螺的穩幅控制和正交抑制，實現了速率積分陀螺的功能；同時，通過微分也能完成速率陀螺的功能。對該系統進行初步測試，得到了該速率積分陀螺的測量范圍，零位漂移等指標。相對于力平衡模式，該系統拓寬了測量范圍，為進一步提升全角半球陀螺的精度奠定了基礎。