探測器陣列靶的激光光斑圖像復原方法研究

程乙輪,何 楓,譚逢富,王振東,秦來安,靖 旭,張巳龍,侯再紅

(1.中國科學院安徽光學精密機械研究所大氣光學重點實驗室,安徽 合肥 230031;2.中國科學技術大學,安徽 合肥 230026)

1 引 言

激光在大氣中傳輸時由于受到湍流、熱暈和消光等因素的影響,激光器出口處激光功率密度分布與遠場光斑功率密度有較大的差異[1]。準確測量激光遠場光斑時空強度分布是直接獲取激光光束質量、激光到靶能量和光斑質心漂移等重要參數的有效手段,對于分析強激光在大氣中傳輸效應研究和評價強激光系統的光束控制能力、瞄準能力等具有重要的意義[2]。

目前,對于遠場激光的光斑能量分布測量方法主要是攝像法和陣列探測法[3]。攝像法采用非接觸式測量,具有結構簡單,易于獲得高分辨率的光斑圖像等優點,但較難實現對光斑空間分布的定量測量,僅適合于激光光斑相對空間分布實時測量[4]。陣列式探測法不受時間限制,具有精度高、實時性好等特點,在對激光器性能的測試中應用十分廣泛。其缺點為需要采用大量的探測器對遠場光斑進行采樣,而且對探測器的均勻性和穩定性有較高的要求。

特別是在對遠場大光斑進行測量時,由于靶板儀靶面尺寸大,所需探測器數量巨大,造成研發成本的急劇升高[5]。因此,利用已知采樣點光斑數據對光斑實現復原是通過探測器陣列靶獲得準確的遠場光斑參數不可避免的問題,解決這一問題的關鍵是尋求一種高精度的插值算法對采樣光斑圖像進行復原。傳統復原方法主要采用最鄰近插值算法和線性插值算法,雖然這兩種算法能滿足陣列靶的實時性要求,但其計算精度低,難以得到準確的遠場光斑參數。相比之下非線性插值算法計算精度高,但其復雜的處理過程增大了對時間的需求,難以在實時性較高的環境中得到應用。本文所提出的算法是一種改進型的非線性插值算法,該算法完美的繼承了非線性插值算法精度高的特點,同時也極大的縮短了算法處理時間。

2 基于改進型雙三次插值算法的光斑復原原理與方法

2.1 探測器陣列法采樣光斑復原原理

光電式探測器陣列靶測量系統是利用激光器發射的激光作為測量系統的輸入量,通過光電轉化模塊處理后的數字信號為輸出量。光電探測器陣列實現光電信號的轉換,光電信號經模塊化處理后實現數字化,最終發送至數據處理終端,完成數據處理和分析[6]。測量系統示意圖如圖1所示,探測器陣列靶靶面探測器分布如圖2所示。當激光照射在探測器表面時,探測器將激光能量響應轉換成相對應的電流響應,通過對所測得電流進行轉化計算得到與采樣光斑相對應探測器位置的灰度值g(x,y),最終在數據處理終端得到完整的遠場光斑圖像。

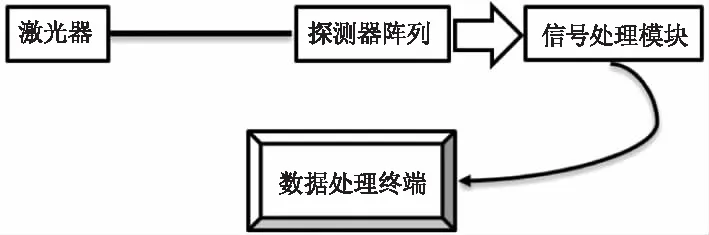
圖1 測量系統示意圖

圖2 探測器分布示意圖

2.2 改進型雙三次插值算法原理

由于靶面探測器分布稀疏,所以很難得到準確的激光測量參數。傳統的雙三次插值算法是利用bicubic核函數對插值點進行擬合計算,bicubic函數如公式(1)所示。該算法最大的優勢是充分考慮插值點與原圖像周圍16個相鄰的像素點的權重系數,將插值點坐標分割為整數部分和小數部分,根據周圍16個點的像素點距離插值點的位置關系按權重系數將其累加從而得到插值點的灰度值[7],該算法雖然增加了程序處理過程中的復雜性但極大的提高了計算精度。

S(x)=

(1)

式中,常數a一般情況下取a=-0.5；x為插值點與周圍點距離的小數部分。假設目標點的坐標為G(i+u,j+v),因該方法考慮到目標點周圍16個相鄰點的位置關系,則目標點的灰度值可由公式(2)、(3)、(4)、(5)得到。

G(i+u,j+v)=A*B*C

(2)

(3)

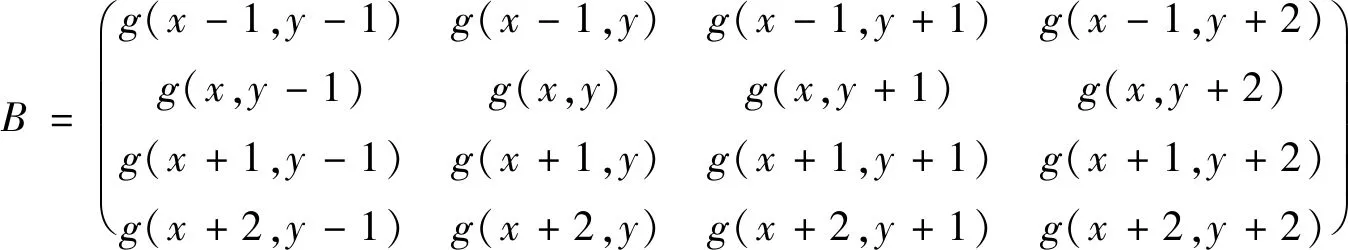
(4)

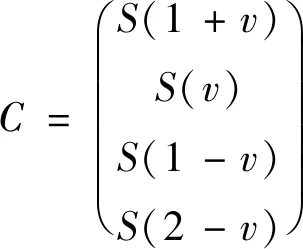
(5)

式中,u和v均為待插值點坐標的小數部分;g(x,y)為原圖像對應點的灰度值。對于傳統的雙三次插值算法在對每個待插值點計算時都要通過公式(1)去計算周圍點的權重系數,再通過公式(3)和公式(4)組成新的矩陣最后進行卷積計算得到完整的光斑圖像。假設采樣光斑分辨率為m×m,插值放大倍率為k,則插值處理后的光斑圖像分辨率為(m×k)×(m×k)。那么u和v將各產生k個不同的值,且其取值范圍為k-1/k到0。假設k取10,則u={0.1 0.2 0.3 … 0.9 0},所以在確定插值倍率的情況下,首先計算出u和v的取值通過公式(1)、公式(3)和公式(5)計算得到矩陣A和矩陣C,然后在插值處理過程中根據u和v的數值去調用矩陣A和矩陣C中對應的系數,這樣就能避免在對每個點進行插值的過程中不斷調用外部函數而造成計算時間的增加,在保證計算精度的同時有效的提升了插值處理時間。

3 仿真實驗

Step1:利用MATLAB生成一幅分辨率為100×100的雙高斯分布的光斑圖像,如圖3(a)所示。根據圖2所示的靶面探測器分布示意圖對圖3(a)所示光斑圖像探測器分布情況進行手動降采樣得到光斑圖像如圖3(b)所示。對圖3(b)所示采樣光斑圖像對圖像像素點提取重新整合得到整合光斑圖像如圖3(c)所示。

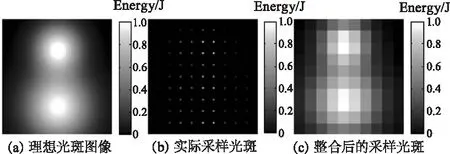
圖3 不同階段光斑圖像

Step2:整合后的光斑圖像分辨率為10×10,為了復原得到原始光斑圖像遂將插值倍率定為10。再分別利用最鄰近插值算法和雙線性插值算法對整合后的采樣光斑圖像以10倍倍率進行插值處理,得到插值后的光斑圖像如圖4(a)和圖4(b)所示。運用雙三次插值算法以相同倍率進行插值處理得到光斑圖像如圖4(c)所示。

圖4 不同算法得到復原光斑圖像

Step3:在確定插值倍率為10以后計算雙三次插值算法中u和v的值,得到u={0.1 0.2 0.3 … 0.9 0 },再通過公式(3)得到矩陣A如下所示,矩陣C為矩陣A的轉置。

(6)

在完成對矩陣A和矩陣C的求取后根據u和v的值在矩陣中調取相對應的元素進行插值最終完成光斑的復原處理,復原得到光斑圖像如圖4(d)所示。

4 仿真結果與分析

分析光斑總能量、質心坐標以及光斑環圍功率是評價光斑復原方法最直接有效的方法。光斑到靶能量能直接反應激光光束在大氣中的傳輸效應,通過對本文提及的幾種不同插值算法得到光斑圖像灰度值進行積分即可得到光斑的到總能量[8],在定量計算中令光斑峰值能量為1 J。求取光斑質心主要有:Hough 變換法、重心法、空間矩定位法[9]。重心法是最直接有效的一種方法。即將光斑視為一個實體,光斑圖像的灰度值視為光斑質量,通過計算其重心得到光斑的質心方法如公式(7)所示。

(7)

式中,x0、y0分別為光斑x軸方向和y軸方向質心坐標；X、Y為圖像x軸方向和y軸方向像素點個數；G(x,y)為圖像灰度值。針對不同的算法得到光斑參數如表1所示。

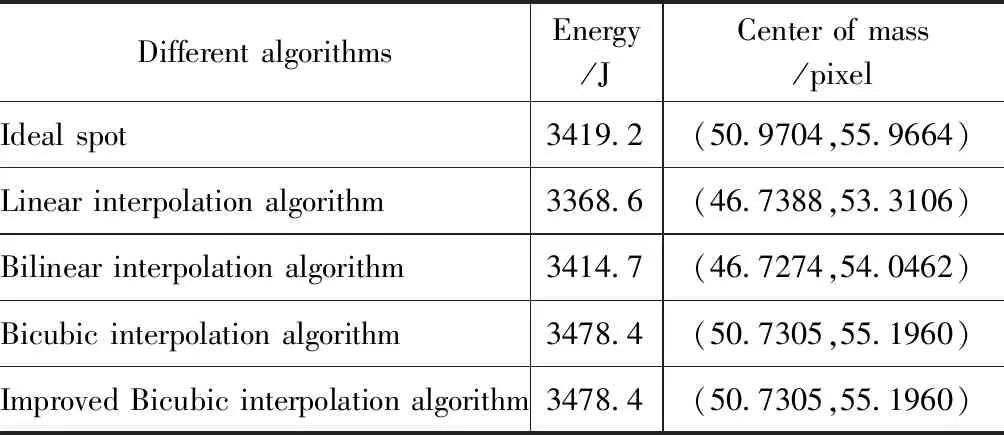
表1 針對不同的算法得到光斑參數

光斑的環圍功率是反映激光集中程度的重要參數,對分析激光系統光束控制能力和跟瞄能力具有重要的意義。所以分析對比理想光斑和復原后光斑的環圍功率能充分的反映算法的準確性。在求取光斑質心坐標后,以質心點處位置為圓心,則半徑為R的環圍區域(記為D0R)內的環圍功率PR可由公式(8)表示[10]：

(8)

式中,G(x,y)為光斑圖像的灰度值。環圍功率PR與光斑總能量的比值即為光斑的環圍功率比,以環圍半徑R為橫坐標,環圍功率比為縱坐標即可繪制出光斑的環圍功率曲線。利用不同算法得到的光斑繪制出的曲線圖如圖5所示。

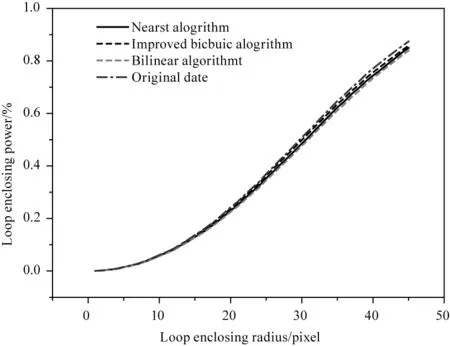
圖5 光斑環圍功率曲線

在應用陣列探測法測量光斑參數時,光斑復原算法所需的處理時間也是一個非常重要的影響因素。圖6為雙三次插值算法和改進后的雙三次插值算法在不同插值倍率下所需時間的曲線圖。

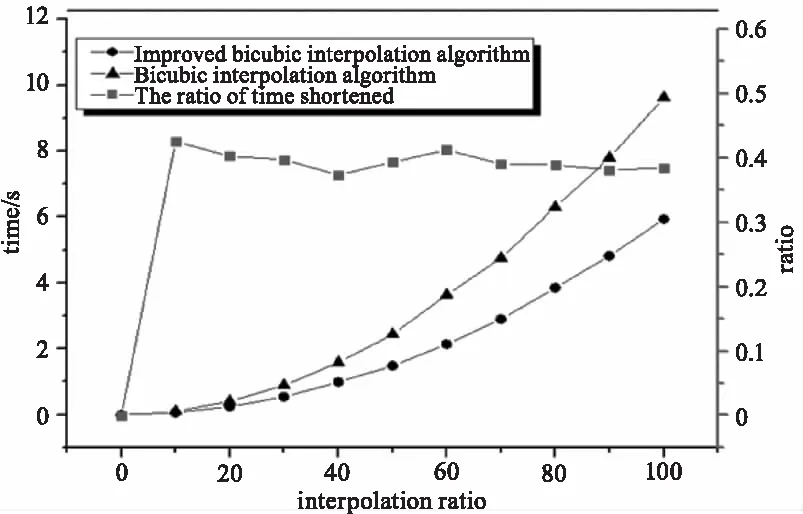
圖6 不同算法在不同插值倍率下處理時間曲線

5 結 論

本文仿真實驗所使用的MATLAB為2014版本,PC機處理器主頻為2.30 GHz的Core i5-6200U。觀察圖4可以明顯看出利用本文算法所復原的光斑清晰度在本文對比的幾種算法中有良好的表現。由表1可以看出本文提出的方法在求取光斑質心坐標時準確性較最鄰近插值算法和雙線性插值算法在x軸方向上均至少提升7.8 %,在y軸方向上至少提升3.3 %。算法優化前后在不同插值倍率下處理速度至少獲得35 %的提升。利用本文優化算法得到光斑的環圍功率曲線更接近原始光斑環圍功率曲線,在環圍功率取63.2 %時運用本文算法計算得到光斑環圍半徑為34.9 pixel,與理想原始光斑圖像相比誤差僅為1.7 %。綜合上述,本文所提出的算法能提升陣列探測法測量遠場光斑參數的準確性,該文為更好的應用陣列探測法提供了一種新的解決方法。