一類二階離散左定Sturm-Liouville問題的譜
王雅麗, 高承華
(西北師范大學數學與統計學院, 蘭州 730070)
1 引 言
近年來, 在許多物理問題中出現了邊界條件依賴特征參數的S-L問題, 引起了諸多學者的廣泛關注并獲得了許多深刻結果[1-4]. 如文獻[2]利用Prüfer變換研究了邊界條件依賴特征參數的特征值問題的S-L理論, 得到了特征值的存在性, 交錯性以及特征值對應特征函數的振蕩性. 文獻[4]得到了連續情形下問題的漸近公式及特征值的交錯性, 對應特征函數的振蕩性等性質.
對邊界條件依賴于特征參數的離散右定S-L問題的譜的研究也已經取得了豐富的結果[5-9]. 如2016年, 文獻[7]研究了如下邊界條件依賴線性特征參數的離散右定S-L問題:
的譜, 其中m(t)>0,t∈[1,T]Z, 即m(t)在[1,T]Z上不變號.對于邊界條件依賴特征參數的離散左定S-L問題的譜研究相對少見. 2017年, 文獻[10]研究了邊界條件依賴線性特征參數的離散左定S-L問題
的譜. 其中,r(t)在[1,T]Z上變號.受以上文獻的啟發, 本文研究如下二階離散左定S-L問題
的譜, 這里Δ是前差分算子, 滿足Δu(t)=u(t+1)-u(t),是后差分算子, 滿足u(t)=u(t)-u(t-1),λ是譜參數,p:[0,T]Z→(0,+),q:[1,T]Z→(0,+),r(t)≠0且在[1,T]Z上變號. 進一步推廣了文獻[10]的結果.
2 預備知識
本文總假定:
(A1) 對所有的t∈[0,T]Z有p(t)>0, 對所有的t∈[1,T]Z有q(t)≥0;
(A2)r(t)在t∈[1,T]Z上變號, 即在[1,T]Z上有m個點使得r(t)>0, 另外T-m個點使得r(t)<0;
(A3)δM正定, 其中δ=ad-bc,
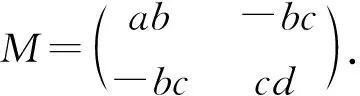
由(A3)可知,δab>0,δcd>0且detM=δbc>0, 于是ac>0,bd>0.
設y(t,λ)是方程(1)滿足初始條件
y(0,λ)=p(0)(cλ+d),Δy(0,λ)=aλ+b
(3)
的解, 則y(t,λ)為如下廣義Sturm序列:
y(0,λ)=p(0)(cλ+d);
y(1,λ)=(a+p(0)c)λ+(b+p(0)d);
(a+p(0)c)λi+Pi-1(λ),i=2,…,T
(4)
這里Pi-1(λ)是關于λ的i-1次多項式. 特別地,
(a+p(0)c)λT+1+PT(λ).
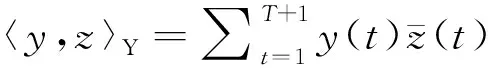
定義H:=Y⊕C. 則H在內積
之下構成Hilbert空間.
定義A:D(A)→H,
A(y,α)=(-(p(t)Δy(t))+q(t)y(t),
-ε(by(0)-dp(0)Δy(0))),
其中D(A)={(y,α)y∈Y, -ay(0)+cp(0)Δy(0)=α},ε=sgnδ. 于是問題(1)-(2)等價于AY=λSY, 這里S=(y,α)=(ry,α).
引理2.1算子A在D(A)上是正定的.
證明 由Hilbert空間中內積的定義可得
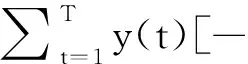
這里f=(y(0),p(0)Δy(0))T, 于是由(A1)及(A3)可知算子A正定.
3 主要結果
引理3.1多項式y(t-1,λ)與y(t,λ),t=1,…,T+1無相同零點.
證明 反設λ=λ0是y(t-1,λ)與y(t,λ)的零點. 則由(4)式可得y(t-2,λ0)=0. 進一步可得y(t-3,λ0)=…=y(1,λ0)=y(0,λ0)=0. 這與y(1,λ0)≠y(0,λ0)=0矛盾.
引理3.2設λ=λ0是y(t,λ)=0的零點, 則y(t-1,λ0)y(t+1,λ0)<0.
證明 由于y(t,λ0)=0, 由引理3.1可知y(t-1,λ0)≠0. 于是由(4)式可知
因此
y(t-1,λ0)y(t+1,λ0)=
由(7)式可知,y(T+1,λ)的最高次項為
(a+p(0)c)λT+1.
因此當λ足夠大時,y(t,λ)的符號取決于a+p(0)c的符號. 若a+p(0)c>0, 則
sgny(T+1,λ)=(-1)T-m+1,λ→-;
若a+p(0)c<0, 則
sgny(T+1,λ)=(-1)T-m,λ→-.

t∈[1,i-1]Z
和方程(1)以及y(i)=0組成問題的特征值. 特別地
則
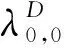
所以不失一般性接下來我們總假定
(A4)δ<0,c<0.
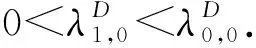
引理3.3多項式y(i,λ)=0與y(i+1,λ)=0,i=1,…,T的根滿足如下交錯性質:
(ii)y(i,λ)=0與y(i+1,λ)=0,i=1,…,T的正(負)根互相分離.
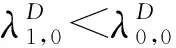
所以當r(1)>0時, 若λ→-則y(2,λ)→+; 若λ→+則y(2,λ)→+.于是y(2,λ)=0有兩個正根且滿足當r(1)<0時, 若λ→-則y(2,λ)→-; 若λ→+則y(2,λ)→-. 于是y(2,λ)=0有一個負根一個正根且滿足因此,y(1,λ)=0與y(2,λ)=0分別有1個, 2個單根且正(負)根互相分離.
不妨假設i=k-1時結論成立, 即y(k-1,λ)=0與y(k,λ)=0分別有k-1個、k個單根且正(負)根也有交錯性. 為簡單起見令


接下來考慮y(k,λ)=0與y(k+1,λ)=0的根的交錯性. 不妨設r(k)>0, 則r(t)在[1,k]Z上有mk-2+2個為正以及k-2-mk-2個為負. 由(4)式可知sgny(k+1,-)=-sgny(k,-),sgny(k+1,+)=-sgny(k,+),以及y(k+1,0)>y(k,0)>0, 且由引理3.2可知
u=1,2,…,mk-2+2,
v=1,2,…,k-2-mk-2.
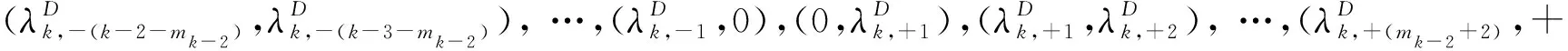
內各有y(k+1,λ)=0的一個根. 另一方面,y(k+1,λ)=0至多有k+1個根. 于是在這k+1個區間內y(k+1,λ)=0只有一個根. 因此y(k,λ)=0與y(k+1,λ)=0的正(負)根互相分離.綜上可知,y(i,λ)=0與y(i+1,λ)=0,i=1,…,T的正(負)根互相分離.證畢.
推論3.4由引理3.3可知, 問題(1),(3)恰有T+1個特征值且滿足
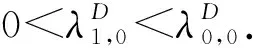
引理3.5假設(A1)~(A4)成立, 則
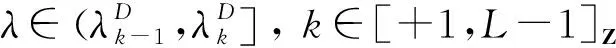

{y(1,λ), …,y(T,λ),y(T+1,λ)}
(5)
變號k-1次. 接下來討論如下序列的變號次數
{y(0,λ),y(1,λ),…,y(T,λ),y(T+1,λ)}
(6)
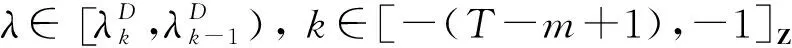
定理3.6假設(A1)~(A4)成立, 則
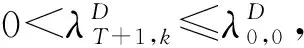
例3.7考慮如下離散左定S-L問題:
其中, |r(t)=16|,r(1)>0,r(2)>0,r(3)<0.則
y(0,λ)=-λ+1,
y(1,λ)=-4λ+3,
y(2,λ)=(2-r(1)λ)y(1,λ)-y(0,λ),
y(3,λ)=(2-r(2)λ)y(2,λ)-y(1,λ),
y(4,λ)=(2-r(3)λ)y(3,λ)-y(2,λ),
由Matlab 7.0軟件計算可得,

即
這與引理3.3的結論一致且問題共有4個特征值, 其中有1個負特征值, 3個正特征值. 接下來我們來驗證振蕩性.
{0.1067, 3.4267, 11.5957, 39.5568, 0},
{0.9599, 2.8396, 2.8978, 1.0970, 0},
{0.8301, 2.3205, -2.4958, -0.5290, 0},
{0.2439, -0.02439, 0.002399, 0.0001702, 0}.
從而可知問題的解y(t,λ),t=0, 1, 2,3,4變號k-1次.這與定理3.6的結論一致.

