非自治Kirchhoff型吊橋方程拉回D-吸引子的存在性

徐 玲， 張娟娟， 馬巧珍

(西北師范大學數學與統計學院, 蘭州 730070)

1 引 言

假設Ω是R2中的具有光滑邊界?Ω的有界開區域. 本文主要討論帶有強阻尼項Δ2ut的非自治Kirchhoff型吊橋方程

拉回D-吸引子的存在性，其中u(x,t)表示橋面在垂直方向的運動，k2>0表示彈性系數，常數p∈R表示作用在橋面末端的軸向外力，當p>0時表示橋被擠壓，否則橋被拉伸,

(F3) |f(u)|≤C2(1+|u|p)，?p≥1，?u∈R,

1990年，Lazer和McKenna[1]討論了吊橋方程

utt+Δ2u+αut+ku+=w(x,t)+f(x)

(2)

弱解的存在性.隨后，諸多學者研究了問題(2)的周期解和數值模擬[2-4].另一方面，鑒于吸引子能夠有效地描述非線性發展方程所產生的動力系統的最終狀態或長時間的發展行為, 很好地反映自然界的許多非線性現象，人們也開始廣泛研究非線性發展方程的吸引子及其性質[5-11]. 特別地，2005年，文獻[5]獲得了耦合吊橋方程全局吸引子的存在性.接著，人們對吊橋方程及耦合系統整體強解和吸引子的存在性進行了廣泛的研究[6-11].如果考慮到橋梁的軸向拉伸而產生的軸向拉力[12]，就得到了Kirchhoff型吊橋方程(1).

在文獻[13]中，當外力項g∈L(R+;L2(Ω))和時，作者獲得了方程(1)有界吸收集的存在性，并在g不顯含時間t時證明了該問題弱解的全局吸引子的存在性及正則性.然而對于問題 (1)拉回吸引子的存在性尚無相關結果.本文運用文[14-15]中的方法研究非線性項滿足條件(F1)～(F3)時問題(1)拉回D-吸引子的存在性.

2 預備工作

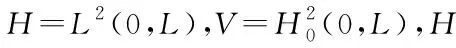
((u,v))，?u,v∈V.

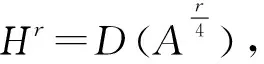
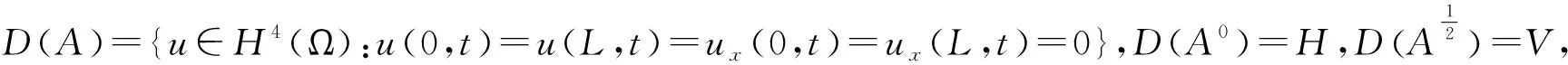
(3)

其中λ1>0是A的第一個特征值.

下面介紹本文用到的基本概念和抽象結論，參見文獻[14-15].

設(E,d)是完備的度量空間，(Q,ρ)為度量空間，也被稱為符號空間.我們定義共圈映射φ:R×Q×E為非自治動力系統，它是由連續的動力系統作用在符號空間Q上而獲得.特別地，θ={θt}t∈R是定義在Q上的動力系統，滿足以下性質：

(i)θ0(q)=q，?q∈Q；

(ii)θt+τ(q)=θt(θτ(q))，?q∈Q，τ,t∈R；

(iii) 映射(t,q)→θt(q)連續.

定義2.1若φ滿足

(i)φ(0,q,x)=x，?(q,x)∈Q×E；

(ii)φ(t+s,q,x)=φ(s,θt(q),φ(t,q,x)x)，?s,t∈R+，(q,x)∈Q×E,

則稱映射φ:R+×Q×E→E是由θ誘導出的共圈映射.

根據上述定義可知，(θ,φ)構成Q×E上的非自治動力系統.

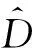
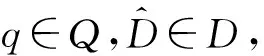
φ(t,θ-t(q),Dθ-t(q))?Bq，

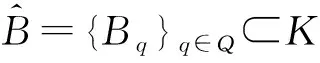
(i)P(∪t≥t0φ(t,θ-t(q),Dθ-t(q)))有界；

(ii) ‖(I-P)(∪t≥t0φ(t,θ-t(q),Dθ-t(q)))‖E≤ε，

則稱(θ,φ)為拉回D-條件(C)，其中P:E→E1是有界投影算子.

定理2.4設(θ,φ)是定義在Q×E上的非自治動力系統.如果

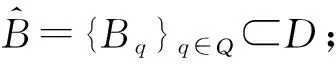
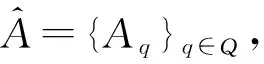
3 主要結果

問題(1)的解的適定性以及解對初值的連續依賴性可由Faedo-Galerkin逼近方法獲得，這里不再陳述，我們直接給出下面的結果.

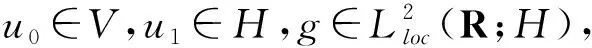
ut∈C(Rτ;V)，ut(t)∈C(Rτ;H)

(4)

其中Rτ=[τ,+).

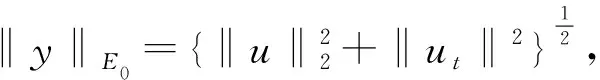
φ(t,τ,yτ0)=y(t+τ,τ,y0)=(u(t+τ),ut(t+

τ))，τ∈R，t≥0，y0∈E0

且

φ(t+s,τ,y0)=φ(t,s+τ,φ(s,τ,y0))，

τ∈R，s≥0，t≥0.

由上述定義可知，映射φ:E0→E0是連續共圈映射.

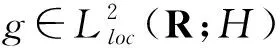
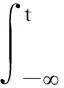
(5)

設Rδ是由全體泛函r:R→(0,+)構成的集合，存在常數δ>0，使得

(6)

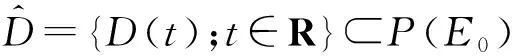
引理3.2[7,9]假設f∈C2(R)，f(0)=0且滿足(F3)，則f:V→H緊連續.

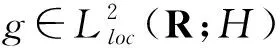
?t∈R,

其中δ>0是常數，Pm:V→span{w1,w2,…,wm}是正交算子.

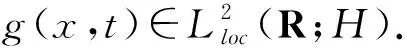
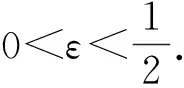
k2(u+,ψ)=(g(t),ψ)-(f(u),ψ)

(7)

由Young不等式和H?lder不等式可得

(8)

(9)

根據條件(F2)可得，存在常數K1>0,使得

(10)

由 (10) 式可得

(11)

由于

(12)

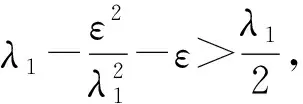
(13)

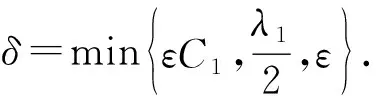
(14)

由條件(F1)可得，存在常數K2>0,使得

?u∈V

(15)

定義

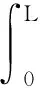
根據 (15) 式有W(t)≥0且

‖g(t)‖2+εp2

(16)

兩邊同時乘以eδt,有

‖g(t)‖2+εp2).

在[t-τ,t]上對上式取積分，可得

(17)

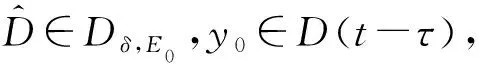
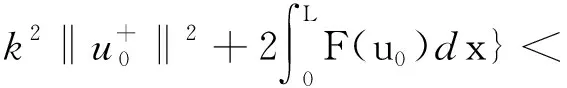
(18)

從而由(15)式可得到

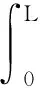
(19)

因此我們有

(20)

令

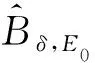
(21)

我們要得到問題 (1) 在E0中存在拉回Dδ,E-吸引子，由定理2.4知，我們只需驗證拉回Dδ,E0-條件(C).

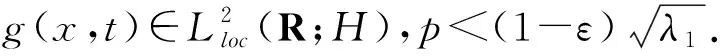
在H中用ψ2=u2t+εu2和方程(1)作內積可得

(g(t),ψ2)-(f(u),ψ2)

(22)

由于

(23)

(24)

由Poincaré不等式，Young不等式和H?lder不等式得

(25)

由于

|f(u),ψ2|≤|((I-Pm)f(u),ψ2)|≤

(26)

|g(t),ψ2|≤|((I-Pm)g(t),ψ2)|≤

(27)

將(23)～(27)式代入(22)式，得到

(28)

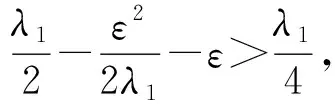
(29)

記

由(4)式可知

(30)

其中

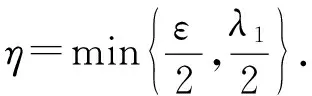
則由(29)式可得到

(31)

上式兩邊同乘eηt可得

(32)

利用Gronwall引理，對上式在[t-τ,t]上積分可得

χ(t)≤χ(t-τ)e-η τ+

(33)

由于

對?t∈R,ε1>0，存在t1∈(t-τ,t),τ1>0使得u(s)=u(s,t-τ,y0)∈Bδ.因此對任意τ≥τ1,s∈[t-τ,τ1],y0∈D(t-τ)有

(34)

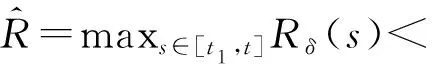
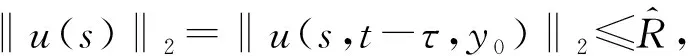
?s∈[t1,t],y0∈D(t-τ).

由引理3.2可知，?ε1>0,m≥m1,τ≥τ1，可得

(35)

再次，由引理3.3，取足夠大的m，使得

(36)

最后，由(6)式可知，存在τ2≥0，使得

(37)

取τ0=max{τ1,τ2}，由(34)～(37)式即得

y0∈D(t-τ).

從而由定理2.4可得到，問題(1)對應的非自治動力系統(θ,φ)在E0中存在拉回Dδ,E0-吸引子.證畢.