相干矢量表象中的量子相干性度量
丁 磊
(西南交通大學物理科學與技術學院, 成都 610031)
1 引 言
由量子態疊加原理產生的量子相干性是量子力學中最重要的基本特征之一,是量子世界從經典領域中分離出來的標志.在跨學科領域中,量子相干性扮演著極其重要的角色,比如納米熱力學[1],量子度量學[2],量子生物學[3]等. 在物理學中,它更是發揮著核心作用,能實現經典物理學和射線光學無法實現的一些應用. 量子相干性是量子物理和量子信息科學中的一個熱門的研究課題,是一些量子應用的基礎條件,如量子隱形傳態[4],量子信息分裂的量子參數估計等.
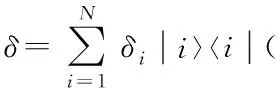

值得關注的是,人們已經注意到,在Baumgratz等人[5]提出的框架中,如果對量子態進行基矢變換,那么就會出現相干態與非相干態相互轉換的情況[10]. 進一步說就是基矢的變換,會導致同一量子態的相干性在同一度量下發生變化. 從物理學的角度出發,物理系統量子態的物理特性在相同度量下不應該隨基矢變換而改變,但是允許其數值隨度量方式的改變而改變. 王偉臣等人[10]已經提出獨立于基矢選擇的度量方式,重新定義的非相干態為經典最大混合態.
本工作在相干矢量表象下提出另一種獨立于基矢選擇的量子相干性度量,稱為相干矢量相干性. 給出了符合相干矢量相干性的非相干態、非相干算符和性質.
2 量子態的相干矢量
在介紹相干矢量相干性之前,本部分將簡短回顧量子態的相干矢量描述及其部分性質. 眾所周知,N維Hilbert空間H中的量子態用密度矩陣ρN來描述,ρN滿足厄米性、正定性和單位跡性. 同時,離散N維Hilbert空間H中的量子態ρN還可以用一個單位算符IN和SU(N)群的生成元展開并得到發展和廣泛應用[11-18]. 其中SU(N)群生成元由如下過程構成[17].
首先,在離散N維Hilbert空間H中的一組正交規范基{|i〉,(i=1,2,…,n)}下引入一組轉換投影算符:
Pij=|i〉〈j|
(1)
然后,利用以下這三組算符
Pll-lPl+1,l+1)

(2)
來構造生成元,其中1≤l≤N-1,1≤j (3) 其中i=1,2,…,N2-1,并滿足如下關系: (4) 利用Tr(ρN)=1,密度矩陣ρN可以表示成如下形式: (5) 根據文獻[16]中的球坐標觀點,在(N2-1)維相干矢量表象B(RN2-1)中,所有可描述密度矩陣的相干矢量形成一個閉合有界凸集,到達該閉合有界凸集邊界上的相干矢量的模長并不相等. 其中純態所對應的相干矢量的模長最大,為: (6) 同時,Schlienz等人[11]已經證明,當對N維Hilbert空間H中的密度矩陣ρN做一個酉變換UN時,該密度矩陣在相干矢量表象中對應的相干矢量做了一個(N2-1)維的轉動O(UN). 基于對密度矩陣做酉變換時,其在相干矢量表象中對應的相干矢量做旋轉的獨特性質,本文在相干矢量表象中利用相干矢量的歸一化模定義了一種新的量子相干性度量: (7) (8) 即為經典最大混合態. 實際上,這樣定義的非相干態是Baumgratz等人[5]定義的非相干態中δi全部相等時的那一類. 王偉臣[10]已經證明,把經典最大混合態作為非相干態時,非相干算符就只能是酉算符UN. 在本文定義的相干矢量相干性度量中,也是把非相干態定義為經典最大混合態,因此本文定義的非相干算符也是酉算符UN. 雖然本文定義的非相干態和非相干算符與文獻[5]中的不同,但是其提出的四個條件卻是普適的,所以本文依然需要依據其條件討論相干矢量相干性的性質. 性質a:非負性,即 0≤Ccv(ρN)≤1 性質b:凸性,量子態的混合態的相干矢量相干性不增大,即 證畢. 性質c:非相干算符作用下的不變性, 即 Ccv(ρN) 總的來說,相干矢量相干性度量完全符合Baumgratz框架的條件(C1)和(C3). 而量子態在非相干算符酉算符UN作用后,不管測量與否,其相干矢量相干性都保持不變. 本文在相干矢量表象中提出了一種新的量子相干性度量,即相干矢量相干性,其實質就是采用相干矢量的歸一化模長來度量量子相干性. 相干矢量相干性能避開相干態與非相干態隨基矢的選擇而相互轉換的問題,也就是對量子態進行幺正變換后其相干矢量相干性保持不變. 本文還在這種度量方式下討論了把非相干態定義為經典最大混合態和把非相干算符定義為酉算符的可行性. 最后,本文還得到了相干矢量相干性的三條性質:非負性、凸性和非相干算符,即幺正算符,作用下的量子相干性不變性. 這對探索量子相干性更好地度量和豐富量子資源理論具有一定的積極意義.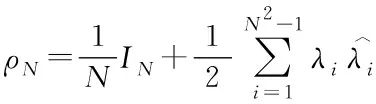
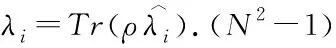
3 相干矢量相干性度量
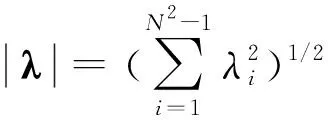
4 相干矢量相干性的性質

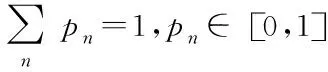
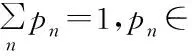
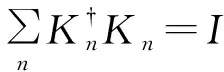
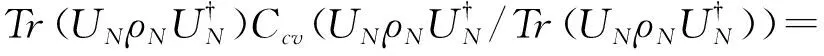
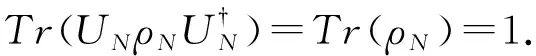
5 結 論

