信息傳播模型發展及其作用機理

曹莫言 彭宇楠

摘? 要? 為了使初學者對信息傳播動力學模型的演化路徑有一個基本的了解，文章以經典的SIR模型為基礎對信息傳播模型的發展過程及其作用機理做了全面的梳理，包括SIS模型、SIRS模型、SI模型、SEIR模型、SCIR模型、CSR模型和SEIRS模型，并對信息模型的演化路徑進行了總結。研究表明，中外學者通過對SIR參數以及路徑的擴充，擴展了其應用領域，并使模型符合信息傳播的規律的實際情況，在遇到輿情危機時更加快速識別并預防危機的進一步擴散。

關鍵詞? 信息傳播模型;發展過程;作用機理

中圖分類號? G354? ? ? 文獻標識碼? A? ? ? 文章編號? 2096-0360（2020）09-0009-05

隨著信息網絡和通訊技術的興起，信息在傳播速度和傳播范圍上顯現出前所未有的活力。網絡媒體時代，信息傳播環境復雜，傳統的信息源及信息傳播路徑發生了巨大的改變，因此，重構網絡信息傳播方式尤為重要。同時，信息傳播與人們的生活密切相關，影響社會價值的實現與安全穩定。網絡媒體傳播過程復雜、影響因素眾多，因此，在對主流媒體網站網絡信息傳播的監測數據分析的基礎上，如何詮釋網絡信息的傳播規律、影響要素及其內在聯系是揭示網絡信息傳播機理需要解決的核心問題。

中外學者除了對經典的傳染病模型進行了豐富的研究，還在這些經典的基礎模型上進行了改進、豐富和發展，但網絡媒體傳播機理的研究尚不完善，對其價值的實現過程缺乏深入研究。因此，信息傳播模型的研究具有很強的現實價值和理論價值。目前，暫未有學者對這些模型按照應用在信息傳播領域的時間進行整理排序，為了方便初學者對模型的初步了解，本文將對傳統模型演化進行歸納總結并啟發信息傳播新模型，在信息傳播上的應用按照時間發展順序進行梳理，總結歸納信息傳播模型的發展過程及其作用機理。

1? 信息傳播動力學模型發展過程

1.1? SIR模型

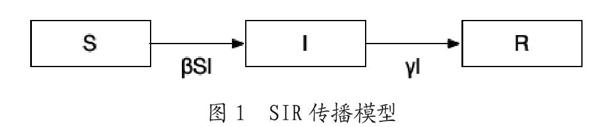
1927年Kermack[1]等最早在黑死病研究中提出SIR模型，將該地區人群分為三類：易感者（susceptibles）其數量記為，即t時刻未染病但可能染病人數。染病者（infectives）其數量記為，即t時刻已染病且具傳染力人數。移出者（removed）數量為，即t時刻已從染病人群移出數。此模型如圖1所示。

1964年Goffman[2]等將SIR模型應用于信息傳播領域，提出用傳染病的動力學模型來研究信息在人群中的傳播擴散。將該地區人群分為三類：易感節點（susceptibles）數量記為，即t時刻未接觸信息但可能接觸信息人數。傳播節點（infectives）數量記為，表示t時刻傳播信息的人數。免疫節點（removed）數量為，表示t時刻對信息免疫的人數。

在信息傳播領域，它建立基于以下三個基本假設[3]。1）此模型用于封閉環境，此環境的總人口恒為一個常數，即，或。2）信息傳播者一旦與信息接收者接觸便有傳播能力。即t時刻，單位時間傳播節點能把易感節點者也變成傳播節點的概率與此環境內信息接收者總數成正比，比例系數為，從而在t時刻單位時間內新的傳播節點為。3）t時刻，單位時間內從傳播節點移出的人數與傳播節點的數量成正比，比例系數為，從而單位時間內新的免疫節點的數量為。

其傳播途徑為傳播節點（I）是信息傳播的源頭，通過一定的概率把信息傳播給易感節點（S）。傳播節點（I）通過比例系數變為免疫節點，免疫節點不可再進行信息傳播。式（1）為SIR模型的作用機理，其中，、分別表示初始狀態下傳播節點、易感節點在總人群中的比例。

SIR模型簡單，適用范圍較窄，但是一個經典的模型，各個模型都是由此發展而來的，此模型適用于倉室較為簡單，同時具備易感節點、傳播節點和免疫節點，并且免疫節點沒有機會再變為易感節點或者傳播節點的情形。

1.2? SIS模型

1932年，Kermack[1]等對模型進行了優化，

首次提出閾值理論，建立SIS模型。1971年G.H.Weiss和M.Dishon[4]將模型應用于數學領域。2001年Romauldo Pasto-Satorras和Alessandro Vespignani[5]將模型應用于信息傳播領域。將該地區的人群分為兩類：易感節點（S）和傳播節點（I），其意義同上。SIS傳播模型可用圖2描述。

其傳播途徑為傳播節點（I）是信息的源頭，通過一定的概率把信息傳播給易感節點（S）。傳播節點（I）以一定的概率被治愈，變為易感節點（S），易感節點（S）接觸傳播節點（I）后會有一定概率進行傳播。式（2）為SI模型的作用機理。其中表示初始狀態下傳播節點在總人群中的比例。

SIS模型適用于信息傳播者停止傳播信息后，通過接觸傳播者，有一定概率變為傳播者的情形，同時，信息傳播者中沒有免疫節點。

1.3? SIRS模型

2004年，Gruhl[6]等基于SIRS傳播模型研究博客網絡話題，將該地區的人群分為S、I、R三類其意義同上，SIRS傳播模型可用圖3描述。

傳播節點（I）是信息的源頭，通過一定的概率β把信息傳播給易感節點（S）。傳播節點（I）通過比例系數γ變為免疫節點（R），免疫節點（R）不可再進行信息傳播，但此后信息傳播者僅暫時免疫，單位時間內將有δR暫時免疫節點再次變為易感節點（S）。式（3）為SIRS模型的作用機理，其中，、分別表示初始狀態下傳播節點、易感節點在總人群中的比例。

SIRS模型適用于傳播節點變為免疫節點后，以一定概率喪失免疫變為易感節點的情形，此模型沒有永久的信息免疫節點。

1.4? SI模型

Hethcote H W和Driessche P V[7]將SI模型在1991年應用于數學領域，Zhao[8]等2009年基于SI模型，提出博客突發性話題傳播模型且引入個體適應度為模型中的經驗參數。將該地區的人群分為S、I兩類，其意義同上。SI傳播模型可用圖4描述。

傳播節點（I）是信息的源頭，通過一定的概率把信息傳播給易感節點（S）。傳播節點（I）無法停止信息傳播。式（4）為SI模型的作用機理，其中，表示初始狀態下傳播節點在總人群中的

比例。

SI模型用以描述那些突然爆發尚缺乏有效控制的信息傳播情景。例如社會危機事件，這種事件受眾數量巨大、信息交互高效、爆發式增長形成網絡輿情。

1.5? SEIR模型

Schwartz I B[9]在1983提出SEIR模型。Stehle J，Voirin N和Barrat A[10]等人在2011年將SEIR模型應用于信息傳播領域。將該地區的人群分為四類：易感節點（S）、潛伏節點（E）、傳播節點（I）和免疫節點（R）。潛伏節點（Exposed）數量記為E（t），表示t時刻接收但不能傳播信息的人數，其余節點意義同上。SEIR傳播模型可用圖5描述。

易感節點（S）在接觸傳播節點（I）之后以一定概率β變為潛伏節點（E），潛伏節點（E）在接觸易感節點（S）時，不可以將易感節點（S）變為傳播節點（I）或潛伏節點（E），接著潛伏節點（E）以一定概率ω變為傳播節點（I），這時候的傳播節點（I）可以將易感節點（S）變為潛伏節點（E）。傳播節點（I）會以一定概率γ變為免疫節點（R）。免疫節點（R）具有永久的免疫力。式（5）為SEIR模型的作用機理，其中，、、分別表示初始狀態下潛伏節點、易感節點、傳播節點在總人群中的比例。

SEIR模型用以描述具有潛伏狀態的情形，潛伏狀態意味著節點接收到信息，但不能傳播，例如某些信息可能需要用戶登陸才能傳播，潛伏節點有一定概率變為傳播節點。

1.6? SCIR模型

Newman M E J[11]在2002提出SCIR模型，Garas A，Argyrakis P和Rozenblat C等人[12]在2010年將SCIR模型應用于經濟領域，Fei Xiong[13]等在2012年將SCIR模型應用于信息傳播領域。將該地區的人群分為四類：易感節點（S）、接觸節點（C）、傳播節點（I）和免疫節點（R）。接觸節點（Contracted）數量記為C（t），表示t時刻已經接收到了信息，但是沒有決定好是否傳播信息的人數，其他節點意義同上。SCIR傳播模型可用圖6描述。

傳播節點（I）是傳染病的源頭，通過一定的概率把傳染病傳染給易感節點（S）使得易感節點（S）變為接觸節點（C），以一定概率使得易感節點（S）變為傳播節點（I）。接觸節點（C）通過比例系數變為傳播節點（I），以比例系數直接變為免疫節點（R），免疫節點（R）不可再進行信息傳播。式（6）為SCIR模型的作用機理，其中，

、、分別表示初始狀態下接觸節點、易感節點、免疫節點在總人群中的比例。k是每個人的平均聯系人數。

SCIR模型用以描述具有接觸狀態的情形，接觸狀態意味著節點接收到信息，但沒有決定好是否傳播，例如某些信息可能不知道真偽，用戶還在觀望。

1.7? CSR模型

2012年，王輝[14]等基于CSR提出移動社交網絡謠言傳播模型，并比對了該模型與CSR 模型、SIR模型的傳播效果。該模型將社交網絡節點分為：輕信者（Credulous），類似于易染者，即指傳播初期未聽到謠言且易相信謠言的群體。傳播者（Spreader），輕信者在聽信謠言后成為新的信息傳播者。理性人（Rationals），類似于免疫者。該模型中理性人存在三種人群，一小部分在傳播開始前便存在，另一部分為傳播者失去傳播興趣后成為了理性人最后一種是在傳播過程中遇到了理性人從而轉變為理性人的。CSR傳播模型如圖7所示。

輕信者（C）在收到傳播者（S）傳播的謠言后，以接受概率p接受這個謠言，并變為新的傳播者（S），傳播概率p是與雙向社會加強有關的概率函數。傳播者（S）在在遇到理性人（R）后以概率v接受理性人（R）說服變為理性人（R）。式（7）為CSR模型的作用機理，其中，、分別表示初始狀態下傳播者和輕信者在總人群中的比例，是每個人的平均聯系人數。

CSR模型用以描述謠言傳播模型，將人群分為輕信者、傳播者和理性人。

1.8? SEIRS模型

陳福集[15]等再2014年提出基于話題衍生性的SEIRS網絡輿情傳播演化模型，通過案例分析對該模型進行數據仿真。將該地區的人群分為四類：易感節點（S）、潛伏節點（E）、傳播節點（I）和免疫節點（R），SEIRS傳播模型如圖8所示。

易感節點（S）在接觸傳播節點（I）之后以一定概率ρ變為潛伏節點（E），潛伏節點（E）在接觸易感節點（S）時，不可以將易感節點（S）變為傳播節點（I）或潛伏節點（E），接著潛伏節點（E）以一定概率β變為傳播節點（I），以一定概率ε變為免疫節點（R）。傳播節點（I）會以一定概率γ變為免疫節點（R）。免疫節點（R）不可再進行信息傳播，但傳播者停止傳播后還，單位時間內將有一定比例δ的免疫節點（R）喪失免疫變為易感節點（S）從而可能再次被感染，將有一定比例τ的免疫節點（R）喪失免疫變為傳播節點（I）進行傳播。式（8）為SEIRS模型的作用機理，其中，

、、分別表示初始狀態下潛伏節點、傳播節點、免疫節點在總人群中的比例，為傳染，是患病率，為治愈率，為直接免疫率，為免疫退化率，為話題衍生率，A為網民隨時間的輸入率。

SEIR模型用以描述具有潛伏狀態的情形，潛伏狀態意味著節點接收到信息，但不能傳播，同時免疫節點有一定概率重新變成易感節點或傳播節點。

2? 信息傳播模型演化路徑及未來趨勢

2.1? 演化路徑

1927年，Kermac[1]等在研究黑死病時提出SIR倉室模型，后學者發現這個模型同樣可以用于信息傳播領域。下面的演化時間是按照模型應用于信息傳播領域的時間順序進行排列的。如圖9所示。

1964年SIR模型應用于信息傳播領域，而后所有的模型都是基于SIR模型發展而來的。2001年模型SIS應用于信息傳播領域，SIS模型去除SIR模型的免疫節點（R），增加了I-S路徑，2004年建立了基于SIRS的博客網絡話題傳播模型，該模型相對于SIR模型增加了一個R-S的路徑，SIS模型無免疫期，免疫節點（R）有一定概率立即變為傳播節點（I），而SIRS模型有暫時的免疫期，節點變為免疫節點（R），節點在這期間不會被感染，會以比例喪失免疫力而變成易感節點（S）。SIR模型中的節點變為免疫節點（R）后獲得了終身免疫。2009年基于SI模型提出了博客網絡中突發性話題的傳播模型，并在模型中引入了個體適應度作為經驗參數，SI模型去除了SIR模型中的免疫節點（R），SI模型中的免疫節點（I）會一直進行信息傳播，2011年SEIR模型應用于信息傳播領域，SEIR比SIR多了一個潛伏節點（E），該節點表示接收到了信息，但不能傳播，潛伏節點（E）以一定概率變為傳播節點（I）。2012年SCIR模型應用于信息傳播領域，SCIR模型比SIR模型多了一個接觸節點（C），該節點表示接收到了信息，但未決定是否進行傳播，同時，值得注意的是，SCIR模型取消了I-R路徑。2012年基于CSR提出了移動社交網絡謠言傳播模型。2014年提出基于話題衍生性的SEIRS網絡輿情傳播演化模型，相對于SEIR模型多了一個R-S路徑，病人康復后只有暫時免疫力，并對其他路徑進行了改進，單位時間內將有比例的潛伏節點（E）失去傳播興趣變為免疫節點（R）。一定比例的免疫節點（R）喪失免疫變為易感節點（S）從而可能再次被感染，將有一定比例的免疫節點（R）喪失免疫變為傳播節點（I）進行傳播。

除上述模型外，還有很多基于上述模型發展，比如顧亦然和夏玲玲[16]在SEIR模型的基礎上，提出一個具有潛伏期的在線社交網絡謠言傳播模型，并給出一種在線社交網絡謠言抑制策略;丁學君[17]構建了基于SCIR的微博網絡輿情話題傳播模型并進行了仿真，表明該模型可以很好地描述微博網絡中的輿情話題傳播規律。王金龍[18]根據在線社交網絡信息傳播特點提出了一種基于用戶相對權重的社交網絡信息傳播模型，討論了不同路徑的信息傳播影響力，并與SIR模型在不同網絡拓撲下進行了仿真實驗。這些模型基于上述模型進行發展演化，從而更加精準地描述信息傳播規律。

2.2? 未來趨勢

隨著人們的生活與互聯網越來越緊密，無線網絡技術、移動終端設備設施的迅猛發展與升級換代，線上交流越來越方便，許多信息都是從線上平臺獲知，例如微信、微博，再如Twitter、Facebook、Instagram等，這些網絡媒體充斥著大量的信息。目前，人們從傳統的看報、廣播和電視等獲取信息的低效又低速到現在信息與移動互聯網、移動媒體結合的高速又高效，信息模型發生了翻天覆地的變化，越來越多的學者基于SIR模型對倉室設置、傳播路徑和異質性方面等進行了改進，使模型更加符合特定信息傳播的規律，除了以上列舉的單一群體模型外，目前很多學者對復合群體模型和微觀個體模型進行了研究。對信息傳播的精準研究有利于政府對謠言等有害因素的控制，從而為大眾創造一個更加安全、高效、智慧、穩定的網絡環境，傳遞更加準確的信息。

3? 結論

本文介紹了信息模型的發展并且對SIR、SIS、SIRS、SI、CSR、SEIR、SCIR和SEIRS模型的傳播路徑、傳播機理和應用等進行了簡單的梳理，以上模型是比較經典的信息傳播模型，目前還有很多新興模型，這些模型也都是根據這些經典模型提出的，學者通過對倉室設置、傳播路徑和異質性方面[19]等進行了改進，使模型更加符合特定信息傳播的規律，節點屬性變化走勢更加接近真實網絡，例如謠言傳播、輿情傳播等，從而更好地模擬出各類網絡媒體的信息傳播規律。

參考文獻

[1]W.O.Kermack，A.G.McKendrick.A Contribution to the Mathematical Theory of Epidemics[J].Proceedings of the Royal Society of London.Series A，Containing Papers of a Mathematical and Physical Character，1927，115（772）：1095-1934.

[2]Goffman W，Newill V A.Generalization of Epidemic Theory： An Application to the Transmission of Ideas[J].Nature，1964，204（4955）：225-228.

[3]李可嘉，王義康.改進SIR模型在社交網絡信息傳播中的應用[J].電子科技，2013，26（8）：168-171.

[4]Ben-Naim E，Krapivsky P L. Scaling behavior of threshold epidemics[J].The European Physical Journal B，2012，85（5）：145-471.

[5]Pastor-Satorras R，Vespignani A. Epidemic Spreading in Scale-Free Networks[J].Physical Review Letters，2001，86（14）：3200-3203.

[6]Gruhl D，Liben-Nowell D， Guha R， et al. Information diffusion through blogspace[J].ACM SIGKDD Explorations Newsletter，2004，6（2）：43-52.

[7]Hethcote H W，Driessche P V.Some epidemiological models with nonlinear incidence[J].Journal of Mathematical Biology，1991，29（3）：271-287.

[8]Zhao L，Yuan R，Guan X，et al.Propagation Modeling and Analysis of Incidental Topics in Blogosphere[M]//Online Communities and Social Computing.Springer Berlin Heidelberg，2009.

[9]Schwartz I B，Smith H L. Infinite subharmonic bifurcation in an SEIR epidemic model[J].Journal of mathematical biology，1983，18（3）.

[10]Juliette Stehlé，Voirin N，Barrat A，et al. Simulation of an SEIR infectious disease model on the dynamic contact network of conference attendees[J].BMC Medicine，2011，9（1）：87.

[11]Newman M E J. Spread of Epidemic Disease on Networks[J]. Physical Review E，2002，66（1Pt2）：016128.

[12]Garas A，Argyrakis P，Rozenblat C，et al.Worldwide spreading of economic crisis[J].New Journal of Physics，2010，12（2）：185-188.

[13]Xiong F， Liu Y， Zhang Z J， et al. An information diffusion model based on retweeting mechanism for online social media[J].Physics Letters A，2012，376（30-31）：2013-2014.

[14] Wang H，Deng L，Xie F，et al. A new rumor propagation model on SNS structure[C]//IEEE International Conference on Granular Computing.IEEE Computer Society，2012.

[15]陳福集，陳婷，鄭小雪.一類新SEIRS模型上的網絡輿情傳播行為研究[J].情報資料工作，2014（4）：62-67.

[16]顧亦然，夏玲玲.在線社交網絡中謠言的傳播與抑制[J].物理學報，2012，61（23）：544-550.

[17]丁學君.基于SCIR的微博輿情話題傳播模型研究[J].計算機工程與應用，2015，51（8）：20-26，78.

[18]王金龍，劉方愛，朱振方.一種基于用戶相對權重的在線社交網絡信息傳播模型[J].物理學報，2015，64（5）：71-81.

[19]張發，李璐，宣慧玉.傳染病傳播模型綜述[J].系統工程理論與實踐，2011，31（9）：1736-1744.