基于熵分析的電動汽車電機及電機控制器熱管理系統研究

李夔寧　鄧廷婷　謝翌　吳存學　王平忠

摘 要：為使能量損失最小，從熱力學的角度對電動汽車電機及電機控制器熱管理系統的串聯構型和并聯構型進行熵分析，得到系統的有效能損失和不可逆度，并通過仿真分析得到兩種構型的系統不可逆度與車速、冷卻液流量和空氣流量的關系。結果表明兩種構型的系統不可逆度隨冷卻液流量和空氣流量的變化趨勢相似，并聯構型在低車速下較串聯構型具有優勢，但隨著車速增加，串聯構型將更具有優勢且占優勢的車速區間更大。最后，以不可逆度最小為目標，對每一車速工況進行最優冷卻液流量和空氣流量匹配。關鍵詞：電動汽車;電機及電機控制器;熱管理系統;熵分析;不可逆度中圖分類號：U469.72 ?文獻標識碼：A ?文章編號：1671-7988（2020）08-09-05

Abstract：?In order to minimize the energy loss， this paper calculated the entropy production of the series configuration and parallel configuration of the thermal management system of the motor and motor controller for electric vehicles from the perspective of thermodynamics， and obtained the effective energy loss and irreversibility of the system. The relationship among the irreversibility， the vehicle speed，?the coolant flow rate and the air flow rate of the two configurations was obtained by simulating. The results show that the trend of irreversibility with coolant flow and air flow of the two configurations is similar. The parallel configuration has advantages over the series configuration at low vehicle speed， but the series configura?-tion will be better as the vehicle speed increases， and its dominant speed range is larger. Finally， this paper aimed at the minimum irreversibility and optimized the optimal coolant flow rate and air flow rate?for each vehicle speed.Keywords： Electric vehicle; Motor and motor controller; Thermal management; Entropy analysis; IrreversibilityCLC NO.： U469.72 ?Document Code： A ?Article ID：?1671-7988（2020）08-09-05

前言

電動汽車的驅動電機通常具有很高的功率密度，會帶來嚴重的溫升問題，從而對電機的運行性能、效率以及使用壽命產生顯著的影響[1]。電機控制器作為驅動系統中的關鍵部件，其控制箱體內的IGBT功率模塊會因為長時間的運行以及頻繁開閉而產生大量的熱量，從而影響電機的輸出特性以及驅動系統的可靠性[2]。目前對電機及電機控制器的熱管理的研究主要集中在電機與電機控制器本身散熱結構的優化上，如文獻[3-5]，對于熱管理系統的單獨研究僅少數學者涉及，如Wulff C等人[6]研究了電機及逆變器的溫度對電驅動系統的效率的影響，以實現冷卻系統中對元件的最優溫度控制。王慶年等人[7]研究了電機及電機控制器的串聯液冷模式，提出了電機最佳冷卻水溫度控制策略。在電機及電機控制器的熱管理結構上，在目前的研究中大多采用了二者串聯的結構，如文獻[8]。

另一方面，電機及電機控制器熱管理系統作為一個能量系統，存在能量的消耗和損失。由于一切實際過程均存在不可逆損失，而熵產是系統不可逆性大小的度量，是系統有效能向無效能轉變造成的，采用熱力學方法對熱力系統或熱力過程進行分析，可以從更本質的層面對系統或過程的能量損失進行優化，實現從根本上節能的目的。Bejan A[9]提出了熵產最小化方法用于熱力系統的優化。Bahmanyar M E等人[10]采用熵產分析方法對垂直蒸汽發生器的性能進行了分析，通過減少熵產來實現垂直蒸汽發生器的性能優化。陳則韶等人[11]研究了熱泵系統的不可逆度，并對熱泵系統的熱力參數進行了優化。熵產分析法在多個領域進行了廣泛研究，然而該方法在電動汽車的熱管理方面卻鮮少有運用。

針對目前電機及電機控制器集成化、一體化的發展趨勢，電機及電機控制器熱管理系統構型單一、系統研究不充分等不足，結合熵產分析方法在能量系統分析上的優點與廣泛運用的基礎，本文在研究過程中主要作出了如下貢獻：同時研究了電機及電機控制器熱管理系統的串聯構型和并聯構型，為電機及電機控制器的熱管理構型設計作出了新的參考;將熵產分析法運用到熱管理系統中，定義了系統的不可逆度，并以此為指標對兩種構型的不可逆性進行比較以及實現運行時冷卻液流量和空氣流量的最優匹配。

1?熱管理系統的熵分析

1.1 熱力學模型分析

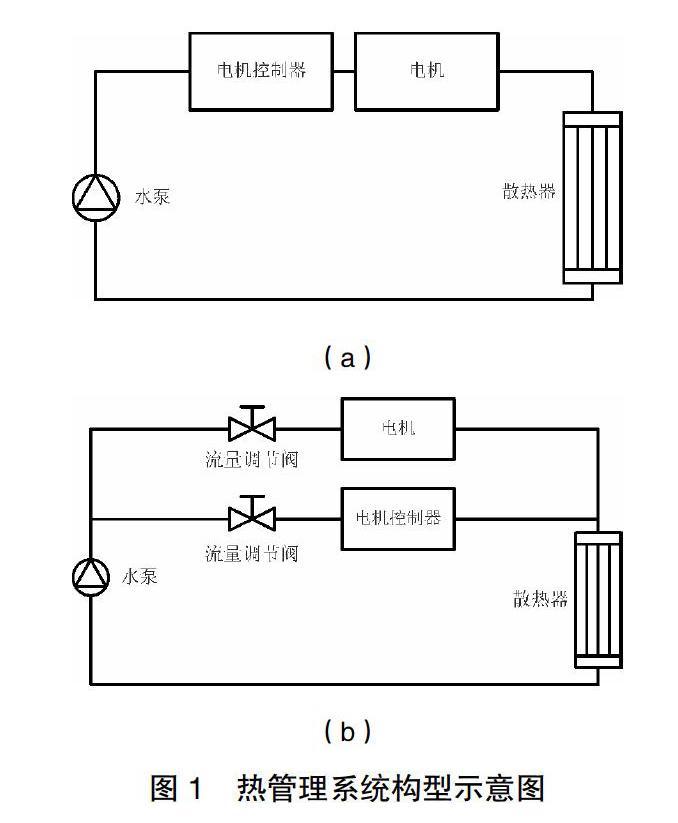
本文研究的串聯形式和并聯形式的熱管理系統構型示意圖分別如圖1中（a）和（b）所示。

對熱管理系統進行熵分析之前，對該系統做如下條件設定：

（1）不計連接管道內熵產損失;

（2）系統處于穩定狀態;

（3）冷卻液為不可壓縮流體;

（4）驅動水泵和流量調節閥內為絕熱流動;

（5）所有流體均視為常物性。

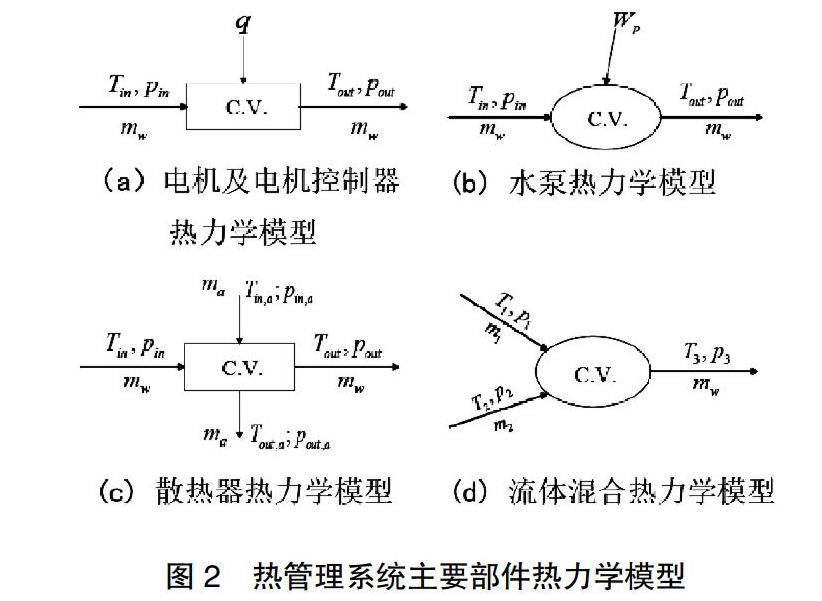
根據圖1所示的構型圖，系統中每一部件均視為控制體積，其中電機水套與電機控制器冷板內的流動及換熱情況類似，其熱力學模型如圖2中（a）所示，水泵的熱力學模型如圖2中（b）所示，散熱器熱力學模型如圖2中（c）所示。在并聯構型下，混合過程存在熵產，其熱力學模型如圖2中（d）所示。

圖中q為電機或電機控制器傳給冷卻液的熱量，Wp為水泵電機輸出的功率，Tin和pin為部件入口冷卻液溫度和壓力，Tout和pout為部件出口冷卻液溫度和壓力，Tin，a和pin，a為散熱器進口空氣的溫度和壓力，Tout，a和pout，a為散熱器出口空氣的溫度和壓力，mw為流過該部件的冷卻液質量流量，ma為空氣質量流量，下標為1、2的參數表示并聯構型中支路的相應參數，下標為3的參數表示混合后相應參數。

1.2?部件及系統的熵分析

在穩定流動的情況下，各部件的熵產計算公式可參考文獻[12]中相應部件的熵產計算式，其中水泵及流量調節閥的熵產Sg計算式為：

各部件的熵產計算式已知后，根據圖1所示構型示意圖，將各部件的熵產相加即可得到的系統熵產。

1.3?系統不可逆度分析

熵產是有效能向無效能轉變造成的，因此系統熵的變化是系統無效能變化的度量。在不可逆過程中，系統的有效能損失為：

對于純電動汽車，動力電池的電能是唯一的能量來源，不可逆過程中損失的有效能最終都是電能的損失。因此本文將系統運行過程中的有效能損失Wu與該過程中電池放出電量E的比值定義為系統的不可逆度，其表達式為：

不可逆度可以評價不同系統的不可逆性，不可逆度越小，則系統的不可逆性越小，通過直接比較不同系統的不可逆度的大小，可以確定哪一個系統更優。對于已給定的系統，可以以不可逆度最小為目標，來優化運行工況，實現節能目的。

2 熱管理系統的仿真分析

2.1 仿真模型的驗證

對于系統仿真模型，本文通過實驗驗證了模型的準確性。實驗過程如圖3所示，驗證結果如表1所示。仿真結果與試驗結果的相對誤差在5%以內，符合實際需求。

完成模型驗證后，本文采用相同的建模方法對另一型號的電機及電機控制器的熱管理系統進行了仿真分析。本文分別計算了兩種構型在環境溫度為35℃時，汽車分別在30km/h、60 km/h和90km/h的車速工況下，穩態運行時電機及電機控制器熱管理系統的冷卻液流量、空氣流量與系統不可逆度的關系，并以最小不可逆度為目標優化得到在合理溫度范圍內的冷卻液流量與空氣流量的最佳匹配。為此，本文將17組冷卻液流量（4L/min至20L/min，以1L/min遞增）與11組空氣流量（0.2kg/s至1.2kg/s，以0.1kg/s遞增）進行正交組合，計算得到每一組空氣流量和冷卻液流量下的各部件和系統的不可逆度，以及各部件出口冷卻液溫度，并從中分析得到系統不可逆度與冷卻液流量、空氣流量的關系，以及符合條件的最優空氣流量和冷卻液流量組合。其中對于并聯構型，冷卻液流量的控制是指主路流量從4L/min至20L/min逐一與空氣流量匹配，電機冷卻支路與電機控制器冷卻支路的流量按1：1進行分配，即支路冷卻液流量是從2L/min至10L/min，以0.5L/min遞增。

本文使用的冷卻液為純水，主要部件溫度控制范圍如表2所示。

2.2 仿真結果分析

2.2.1?系統不可逆度與冷卻液流量、空氣流量的關系

從仿真結果分析發現，串聯構型和并聯構型的系統不可逆度隨冷卻液流量和空氣流量的變化趨勢相似，本文以串聯構型為例進行分析，兩構型的區別在下一部分討論。圖4和圖5分別從不同角度反映了串聯構型分別在車速30 km/h至90km/h時系統不可逆度與冷卻液流量和空氣流量的關系。

從圖4中可知，車速在30km/h時，冷卻液流量一定，在空氣流量較小的情況下，隨著空氣流量的增加，系統不可逆度快速增加，在空氣流量為0.5kg/s左右時，系統不可逆度達到極大值，然后隨著空氣流量增加不可逆度快速降低，在0.8kg/s時達到極小值，之后隨空氣流量增加系統不可逆度先出現小幅上升然后緩慢下降，即系統不可逆度會出現兩次極大值，一次極小值。而隨著車速、冷卻液流量的增加，極值出現的趨勢逐漸減弱。車速60km/h時，每一冷卻液流量下，均只有一個極大值，至90km/h，極值趨勢已不明顯。綜上所述，在低車速時，系統不可逆度會隨著空氣流量的增加呈現波動變化，出現兩次極大值和一次極小值，而隨著車速的增加，第二個極大值、極小值和第一個極大值將逐漸消失而出現空氣流量與系統不可逆度呈負相關的趨勢，車速越大，趨勢越明顯，且這種趨勢是從小冷卻液流量開始逐步變化的，流量越小，趨勢越明顯。

從圖5中可以看出，車速30km/h時，冷卻液流量在10L/min以下時，隨著冷卻液流量的增加，系統不可逆度變化小，冷卻液流量在10L/min以上后，隨冷卻液流量的增加，系統不可逆度近似線性增加;車速在60km/h和90km/h時，系統不可逆度隨冷卻液流量的變化趨勢相同，均隨著冷卻液流量的增大而降低，并在冷卻液流量較大的情況下，下降趨勢變平緩，該變化趨勢與30km/h車速下的變化趨勢相反。本文以串聯構型為例，對比了30km/h和60 km/h車速在0.6kg/s的空氣流量下，各部件在不同冷卻液流量下的熵產，如表3所示。

結合表3與上文各部件的熵產計算式，水泵的不可逆損失主要由流體流動引起，其余三部件的不可逆損失則是由不等溫傳熱和流體流動兩部分引起。而由表3可知，在四個部件中散熱器的不可逆損失最大，約占總不可逆損失的90%。在低車速下，電機及電機控制器發熱量小，隨冷卻液流量的增加，各部件進出口流體溫差變化小，則傳熱不可逆損失變化小，系統的不可逆損失主要受流體流動影響，因此在30km/h車速時，隨冷卻液流量的增加，系統不可逆度會增加。當車速為60 km/h時，電機發熱量增大，各部件進出口流體的溫差增大，系統的不可逆損失主要受傳熱的影響，盡管隨冷卻液流量的增加，由流體流動引起的不可逆損失增大，但流體的進出口溫差減小，傳熱不可逆損失減小，其中散熱器的不可逆損失減小較多，因此系統不可逆損失隨冷卻液流量的增加而出現減小的趨勢。

2.2.2 串聯構型與并聯構型的比較分析

為了比較串聯構型與并聯構型的差異，本文對比了每一車速下空氣流量分別在0.3kg/s、0.6kg/s、0.9kg/s和1.2kg/s時，串聯構型與并聯構型在相同冷卻液流量下的系統不可逆度的差值，如圖6所示。

車速為30km/h時，在相同工況下，差值均為正值，串聯構型的系統不可逆度大于并聯構型的系統不可逆度。車速在60km/h和90km/h時，除部分小空氣流量和小冷卻液流量的組合中串聯構型的系統不可逆度大于并聯構型的系統不可逆度外，其余情況均為串聯構型的系統不可逆度小于并聯構型的系統不可逆度。

在上述分析中，值得注意的是，當車速大于等于60 km/h后，對于冷卻液流量較小時出現的串聯構型系統不可逆度大于并聯構型的情況，在運行過程中，電機及電機控制器的出口冷卻液溫度會大于其允許溫度，達不到散熱需求，因此在實際運行時，并不允許這種冷卻液流量與空氣流量的組合。即實際運行時，在?60km/h至90km/h時，串聯構型的系統不可逆度均小于并聯構型的。由此可見，并聯構型的優勢主要在車速較小時體現，車速較大時則是串聯構型更具有優勢，且從圖6可知，串聯構型占優勢的車速區間更大。

2.2.3 兩種構型的冷卻液流量和空氣流量的最優匹配

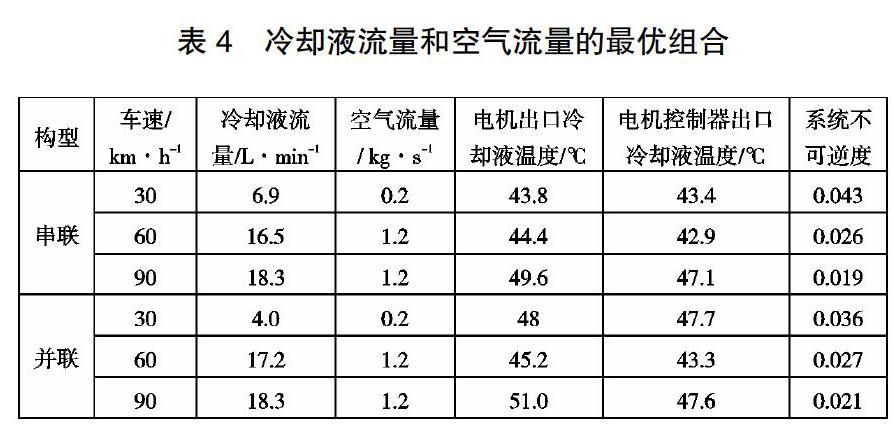
本文采用MATLAB對每一種構型在每一車速條件下的187組數據進行擬合，最終得到相應車速條件下滿足溫度要求的不可逆度最小的空氣流量和冷卻液流量組合，如表5所示。

3 結論

（1）串聯和并聯構型的系統不可逆度隨空氣流量和冷

卻液流量的變化趨勢相似;

（2）并聯構型的優勢主要在車速較小時體現，車速較大時則是串聯構型更具有優勢，且串聯構型占優勢的車速區間更大;

（3）采用熵產分析方法可實現熱管理系統運行參數的優化。

參考文獻

[1] 和偉超.電動汽車用永磁同步電機水冷系統設計及溫升分析[D].浙江大學，2013.

[2] 姜坤，李濤，張永亮.電機控制器IGBT模塊水冷散熱研究[J].電子科技，2017，30（2）：68-71.

[3] CAVAZZUTI M，GASPARI G， STEFANO P，et al.?Thermal manage?-ment of a Formula E electric motor： Analysis and optimization[J].?Applied Thermal Engineering， 2019， 157： 113733.

[4] KYUHO S，YONG-BOK L，SEOK-MYENG J，et al.Thermal analysis of high-speed permanent magnet motor with cooling flows supported on gas foil bearings： part I-coupled thermal and loss modeling[J]. Journal of Mechanical Science and Technology， 2015， 29（12）： 5469-5476.

[5] ILYIN M V， VILKOV E A， GULYAEV I V. A thermal model of an IGBT module taking into account thermal interconnections between chips[J]. Russian Electrical Engineering， 2019， 90（1）： 6-10.

[6] WULFF C， MANNS P， HEMKEMEYER D， et al. Choice of energetically optimal operating points in thermal management of electric drivetrain components[C]//Energy and Thermal Manage?-ment，?Air-Conditioning， and Waste Heat Utilization， 2019： 3-14.

[7] 王慶年，韓彪，王鵬宇，等.電動汽車冷卻系統設計及電機最優冷卻溫度控制[J].吉林大學學報（工學版），2015，45（1）：1-6.

[8] CHOWDHURY S， LEITZEL L， ZIMA M， et al. Total thermal man?-agement of battery electric vehicles （bevs）[J]. SAE Technical Paper， 2018， 37（26）： 1-7.

[9] BEJAN A.Entropy Generation minimization： The new thermodyna?-mics of finite-size devices and finite-time processes[J]. Journal of Applied Physics， 1996， 79（3）： 1191-1218.

[10]?BAHMANYAR M E， TALEBI S.A performance analysis of vertical steam generator using an entropy generation method[J].?Annals of Nuclear Energy， 2019， 125： 212-221.

[11]?陳則韶，李川，江斌.熱泵系統的不可逆度及其熱力參數優化[J].工程熱物理學報，2015，36（06）：1159- 1163.

[12]?LI H， FIGLIOLA R. Optimization of an automotive cooling system based on exergy analysis[J]. SAE Technical Paper， 2004， 1： 1-13.

[13]?王洋.流動與混合過程中不可逆損失的研究[D].哈爾濱工業大學， 2008.