機場出租車可插隊排隊問題研究
徐若寅

摘 要:在機場、高鐵站、客車站等大型運輸樞紐中,常常會有出租車蓄車池的存在,伴隨的問題是如何優化出租車的資源。但是因為這些客運站距離市區較遠,如果乘客的乘車距離較短,就會造成運送他們的出租車收益較低的情況,本文根據采用可插隊排隊論模型【1】,以一個機場舉例,探究了出租車在蓄車池中的運行規律,給予部分出租車插隊的權利。
關鍵詞:大型運輸樞紐;出租車資源調度;可插隊排隊論模型
一、問題闡述
以一批次C輛出租車為單位,假設客流量充足,具有優先權的出租車會在優先等待區等待,當具有優先權的出租車達到一個批次的數量且當前載客批次的出租車全部載客駛出乘車區時,具有優先權的出租車可以駛入乘車區。
擁有優先權的出租車很難有需要排隊的情況,而普通出租車的數量也會處于動態平衡中。
假定出租車隊伍中有Z輛出租車時,出租車的到達率等于運行過程中的平均到達率K1,如果任意一輛無優先權的出租車進入蓄車池,那么它前面的出租車數在Z上下波動。所以如果暫時忽略前方Z輛出租車,則本問題可等同于一批乘客對一批出租車服務的具有優先級的排隊論模型。
則滿足一個批次的平均到達率為K_1/C批次/min,即服從泊松分布,其中D%是搭載過短程旅客的具有優先權的出租車比例。一個批次出租車在乘車區等待乘客滿足等上一個批次的數量需要時間N,服從指數分布。
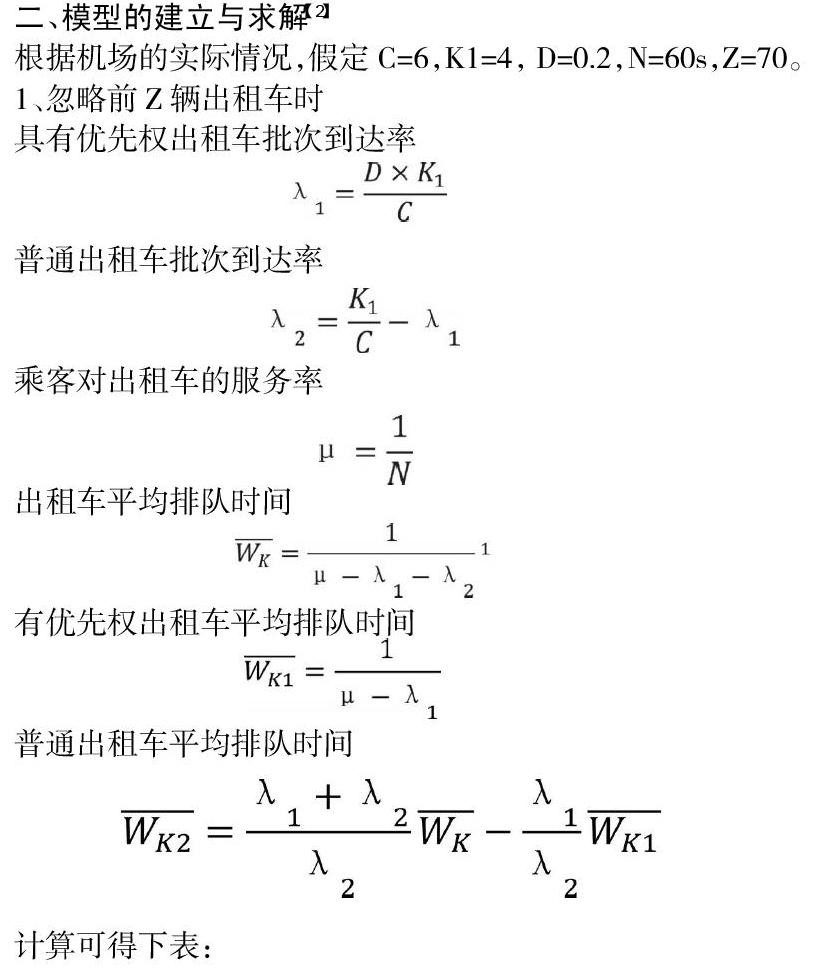
二、模型的建立與求解【2】
根據機場的實際情況,假定C=6,K1=4, D=0.2,N=60s,Z=70。
三、結語
本文依據出租車蓄車池的基本情況,采用了可插隊排隊論模型,會給予短途載客再次往返的司機一定的“優先權”,緩解了部分短程出租車收益較低的問題。
參考文獻:
[1]弗雷德里克.S.希利爾,杰拉爾德.J.利伯曼.運籌學導論[M].第8版.北京:清華大學出版社,2007.8:747-791.
[2]姜啟源,謝金星,葉俊.數學模型[M].第5版.北京:高等教育出版社,2018.5.

