曲軸扭振分析CAE 方法改進與探討

彭宇明 甘金科 劉 磊 羅 振 吳有彬

（1-先進驅動節能技術教育部工程研究中心 四川 成都 610031 2-西南交通大學機械學院 3 柳州龍杰汽車配件有限責任公司）

引言

扭振是指具有扭轉彈性的軸系所做的各截面間存在幅值和相位差的角振動。曲軸在受到大小和方向都作周期性變化的激勵力矩時會產生較大的扭轉振動，這樣會給發動機工作可靠性、穩定性和發動機性能帶來很大影響，甚至會導致曲軸斷裂[1]，引發重大事故。因此，發動機及附件的設計制造都對軸系扭振計算具有非常強烈的要求和重要的意義。采用集總參數模型與分布參數模型都可以對發動機曲軸系的扭振進行計算[2]，不過對具有復雜幾何邊界的曲軸系進行精確的扭振分析具有較高難度，目前工程界常采用集總參數模型進行軸系的扭振計算分析。

一些商用軟件如AVL-excite、GT-power 等都提供基于集總參數法進行軸系扭振計算的快速工具，計算結果的置信度始終有較大的困擾。集總參數法對曲軸系統進行準確的扭振分析需要盡可能求得相對精確的轉動慣量和扭轉剛度數據，各集中質量點的轉動慣量可以依靠三維建模軟件準確獲得，各集中質量點之間的剛度為半拐結構的扭轉剛度，半拐扭轉剛度的準確計算則是影響分析結果的關鍵點。

以某四缸汽油機曲軸系為研究對象，針對目前工程上普遍采用的集總參數法中對計算結果影響較大的半拐剛度計算進行了深入的分析和探討，改進了半拐扭轉剛度有限元計算分析方法，使計算結果更符合實際運轉情況；提出了快速有效的對軸系扭振集總參數模型置信度的校核方法，通過臺架試驗對扭振計算結果進行了驗證對比。

1 半拐剛度的計算方法

1.1 經驗公式法計算半拐剛度

經驗公式主要針對單位曲柄進行計算，曲柄結構由2 個半段主軸頸、2 個曲柄臂、以及一個曲柄銷所組成，如圖1 所示。其剛度是這3 部分剛度的合成，并且在計算中做了如下假設：不考慮單位曲柄組成部分相互間的影響；將曲柄臂認為是一個純彎曲梁；主軸頸、曲柄銷作純扭轉變形。根據材料力學的相關公式即可算得曲柄結構的基本剛度公式，其值的2 倍即為半拐剛度值。

其他的經驗公式還包括西馬連科（Zimanenko）公式、克·威爾遜（Ker Wilson）公式、中國船級社推薦公式等，這些公式都具有不同的適用范圍，曲柄上的油孔結構、曲柄臂復雜的幾何邊界等因素對計算結果也具有一定的影響，若要在工程上采用公式法進行半拐剛度的計算，則需要進行廣泛的修正，但通常難以得到較為準確的計算結果。

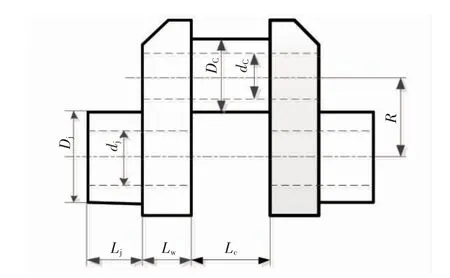
圖1 單位曲拐圖

中國船級社推薦公式：

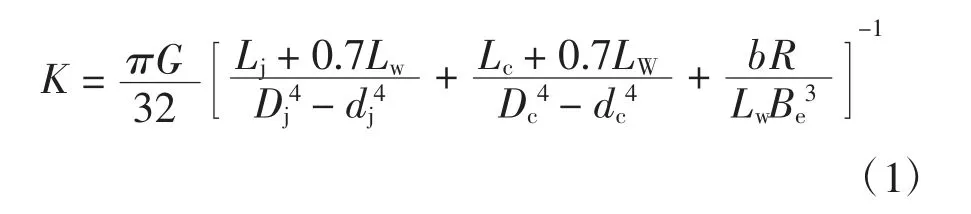
其中曲柄銷與主軸頸有重疊度時b=0.7；無重疊度時b=0.8。

1.2 仿真方法計算半拐剛度

1.2.1 商用軟件剛度算法

在AVL-excite、GT-power 等軟件中提供了一種基于幾何型面特征的半拐剛度工程計算方法，該方法實質上也是基于修正的經驗公式進行計算，忽略了主軸頸、曲柄臂、曲柄銷各部件之間的彈性變形影響。使用者通過輸入組成半拐結構的曲柄銷、主軸頸、曲柄臂3 部分的幾何參數，軟件會自動進行扭轉剛度的計算，由于不能表達所有的細節特征，其計算精度往往不高，計算結果用于一維扭振當量計算與臺架試驗容易出現一定的偏差，有時偏差還較大，所以軟件本身也不建議采用此方法來作為主要精確計算扭振的依據。

1.2.2 有限元方法計算半拐剛度

有限元法計算半拐剛度可以充分考慮到模型表面的幾何特征以及各部分結構之間的彈性變形和阻尼的影響。文獻[3-6]中都提到了采用有限元方法計算曲柄或半拐的扭轉剛度，其計算邊界條件都是在一端施加全約束而在另一端直接施加扭矩，不過這種邊界條件的加載方法與半拐結構實際的受力情況不太相符。此外，在后處理部分扭轉剛度的計算中，影響計算精度的關鍵點也沒有提及，所以文獻中針對半拐扭轉剛度的精確計算過程看似合理，但還存在一定偏差，還需進一步分析。

2 半拐剛度有限元優化計算方法

2.1 有限元模型的建立

所提出的計算方法同樣基于有限元法。創建半拐三維模型（包含半個主軸頸、半個曲柄銷、一個曲柄臂結構）并進行適當簡化處理，得到半拐模型如圖2 所示。

圖2 半拐模型

采用ansys 軟件建立有限元模型，由于半拐模型表面具有較復雜的曲面邊界，選用solid187 二階四面體單元劃分網格。半拐的材料參數為：彈性模量210GPa，泊松比0.3。

2.2 邊界條件的施加

對半拐模型施加邊界條件應該考慮與實際受力情況相符，以此保證扭轉剛度計算結果盡可能與實際情況相符。曲軸上各個曲拐結構承受著連桿大頭傳遞過來的力而相互扭轉，致使曲柄銷有繞主軸頸軸線扭轉的趨勢，因此這里提出計算半拐剛度的邊界條件為：主軸頸端面施加全約束，曲柄銷端面施加以主軸頸軸線為軸心的扭矩。在主軸頸軸線上建立質量單元，通過將該質量單元與曲柄銷端面節點耦合的方式以實現上述邊界條件的加載，如圖3 所示。

2.3 基于扭轉中心的半拐剛度計算

圖3 邊界條件的施加

實際扭轉中心的提取是計算扭轉半徑的關鍵，也是正確求解扭轉剛度的基礎。文獻[7-8]中在計算相對扭轉角時將主軸頸軸線作為扭轉中心。理論上，扭轉中心是零變形點，以主軸頸軸線施加扭矩其扭轉中心應該位于該軸線上，但實際上曲軸是個彈性體，再加上各部分的相互約束作用，會導致扭轉中心發生偏移，半拐結構受力變形的實際扭轉中心位于曲柄銷端面靠下的位置，如圖4 所示。經計算若是采用主軸頸軸線作為扭轉中心，計算結果偏差可能會高達20%以上。此外網格離散程度的不同會影響扭轉中心的獲取。在劃分網格時需要對曲柄銷端面扭轉中心處的網格進行加密處理，如圖2b 所示。計算后的半拐變形云圖如圖5 所示，可見曲柄銷端面變形位移最小點確實位于該端面靠下的位置，該點即為扭轉中心點。

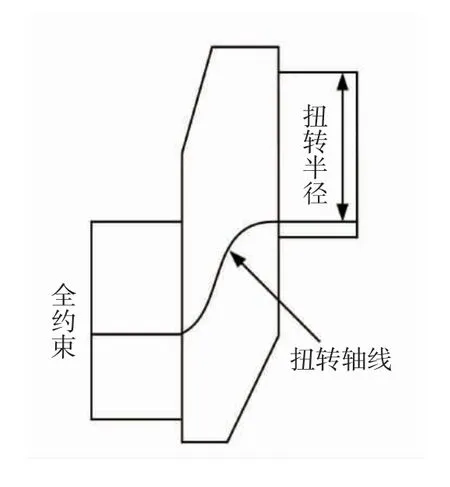
圖4 半拐扭轉軸線示意圖

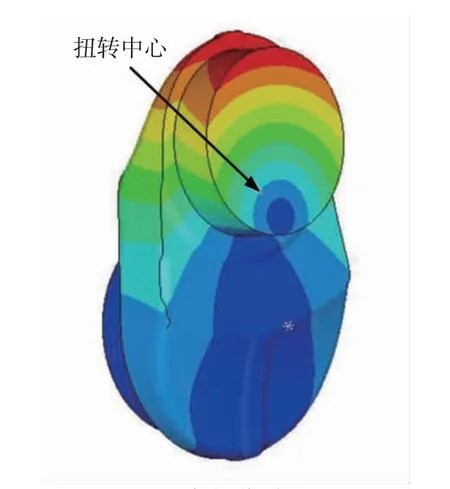
圖5 半拐位移云圖

表1 為分別采用經驗公式法（中國船級社推薦公式）、AVL 軟件計算法和優化計算法計算的半拐剛度數據匯總，以及前2 種計算方法與優化計算方法剛度值之間的相對誤差，從表中可以看出采用不同的計算方法半拐剛度值具有較大的差異，其中采用經驗計算方法最大的誤差值達到了21%。

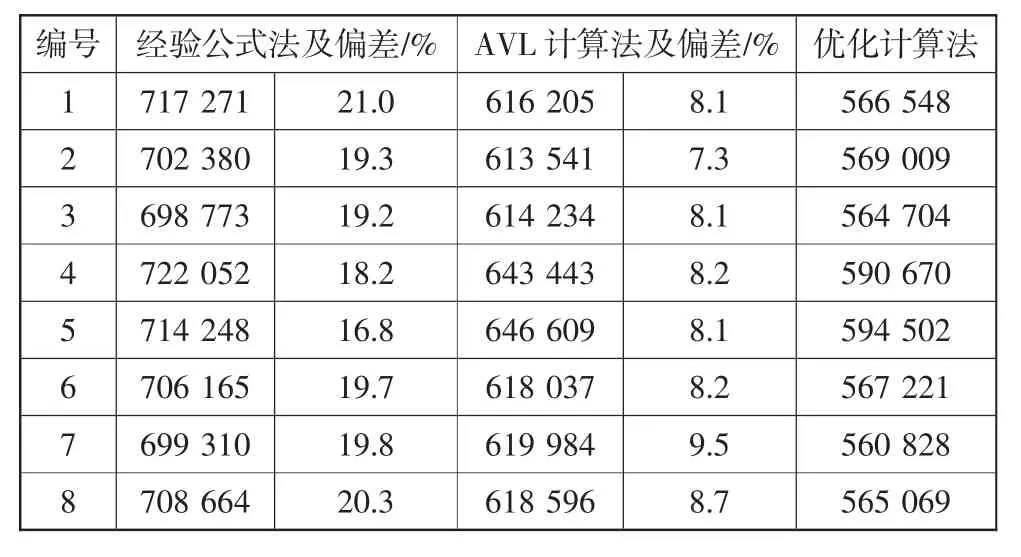
表1 采用不同方法計算的半拐扭轉剛度 N·m·s/rad

3 快速檢驗與校核

檢驗剛度計算準確性最準確的方法是通過實驗測試，但測試半拐剛度的實驗相對困難復雜。通常，三維曲軸的扭振模態分析結果是比較可靠合理的，通過一維集總參數扭振計算結果與其進行對比，可以快速地判斷集總參數模型的合理性，此外通過與臺架強迫扭轉振動測試結果進行對比，以間接驗證半拐剛度計算方法的準確性。

3.1 三維有限元扭振模態分析

建立包含皮帶輪和飛輪部件的曲軸模型，導入ansys workbench 軟件建立有限元模型。利用動能相等原理將活塞連桿組質量等效為集中質量點加載到對應曲柄銷中心位置。此外，對曲軸系模型進行模態分析需設置適當的約束條件以反映曲軸系的實際工作狀態，在主軸頸處施加徑向約束以便于得到軸系準確的扭振特性[9]。軸系前2 階扭轉模態如圖6 所示，其中一階扭轉固有頻率為491.4 Hz，二階扭轉固有頻率為1 101.7 Hz。

3.2 集總參數模型校核

采用表1 中的各組剛度數據并在AVL-excite 軟件中建立軸系扭振仿真分析模型。求解曲軸系的自由振動微分方程即求得曲軸系的扭振固有頻率和振型，主要關注前2 階低頻率下的振動，高階振動一般不會在發動機轉速范圍內出現共振。采用各組剛度數據和有限元方法計算的軸系扭振固有頻率如表2所示，可見采用優化計算方法剛度數據所得軸系固有頻率與有限元法計算結果最為接近，說明采用優化計算方法的結果精度更加可靠。

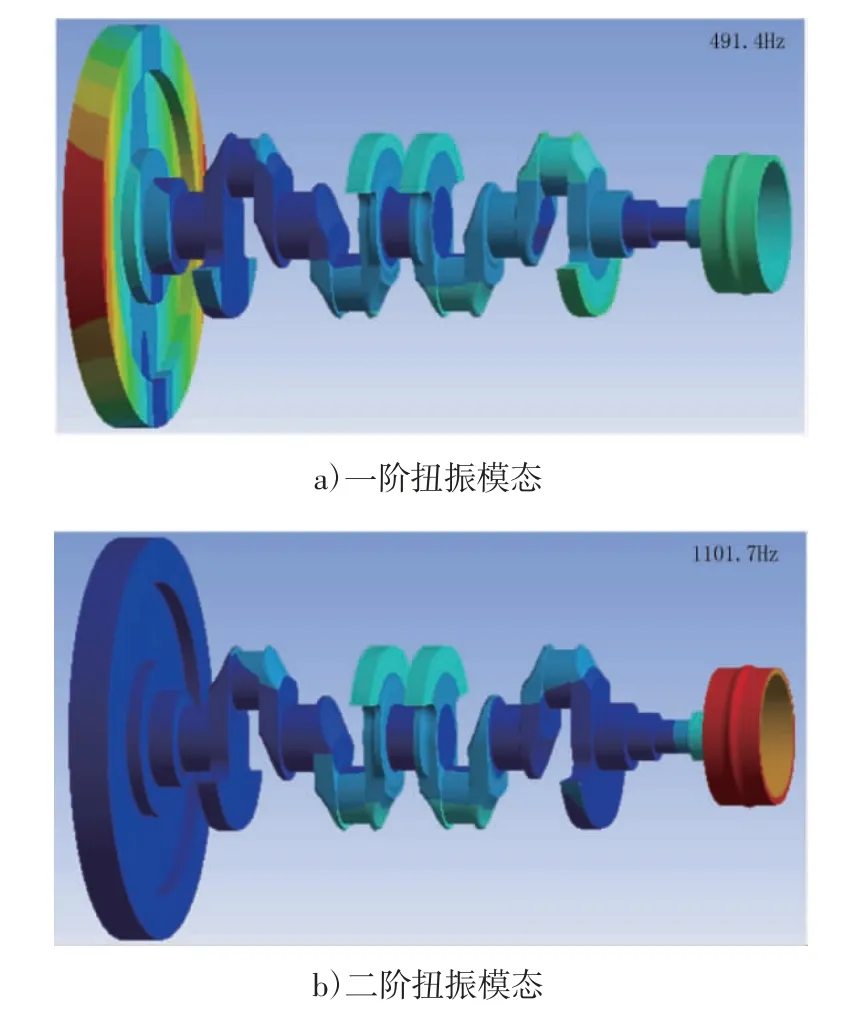
圖6 有限元模型固有特性分析

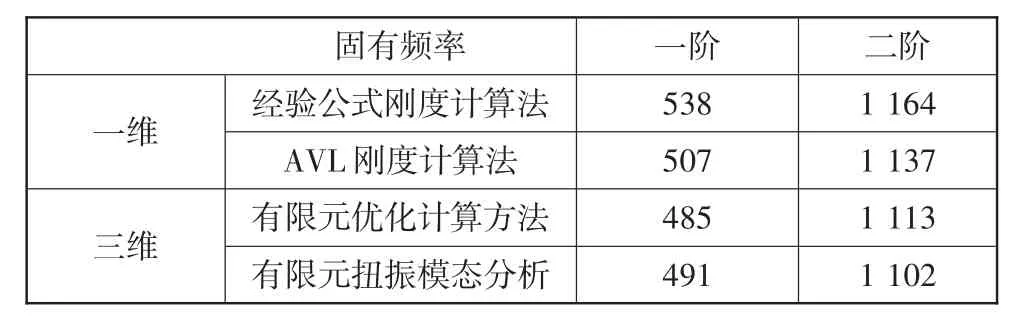
表2 不同剛度計算方法的軸系集總參數模型固有頻率與三維計算結果對比 Hz

4 扭振試驗與仿真結果對比

在發動機臺架上進行扭振試驗，數據采集系統和分析軟件為ANZT10 扭振測試儀及其配套軟件，測得轉速范圍在1 000 rpm 到5 500 rpm 之間曲軸前端扭振角位移隨轉速變化的曲線。在扭振試驗過程中，通過在曲軸前端安裝光電編碼器來測得扭轉振動的角位移，如圖7 所示。

圖7 臺架試驗臺以及傳感器安裝

圖8 為帶減振器并采用優化方法剛度數據的強迫振動各諧次仿真結果和試驗結果的對比。由于2諧次波受滾振影響較大，在工程上對軸系的運行可靠性影響較小，這里主要對比分析4、6、8 主諧次波。其中試驗結果4 諧次臨界轉速和對應扭振振幅分別為4 300 rpm/0.114°，6 諧次臨界轉速和對應扭振振幅分別為3 050 rpm/0.036 5°，8 諧次臨界轉速和對應扭振振幅分別為4 250 rpm/0.069 2°、2 250 rpm/0.036 8°，并且從圖中可看出仿真和試驗各諧次的扭振振幅變化趨勢完全一致，共振點對應的臨界轉速基本相同。個別諧次波仿真結果和試驗結果的扭振振幅值有一定偏差，4 諧次中在低轉速段出現較大的偏差是由于滾振導致的測試誤差，以及模型中一維阻尼參數的取值依照工程經驗所設置的，工程上在合理的范圍內。

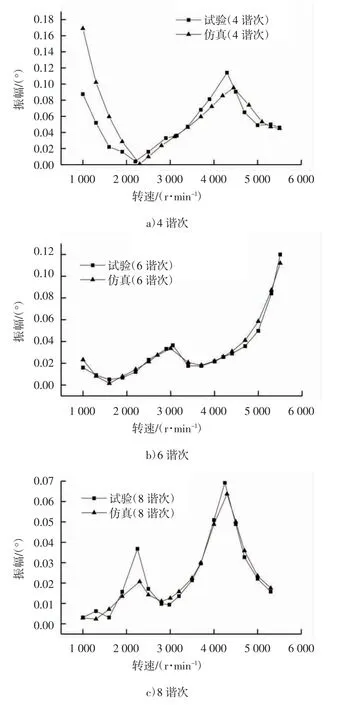
圖8 仿真與試驗各諧次扭振振幅對比

5 結論

為了準確求得集總參數模型中的剛度參數，建立了半拐有限元模型，分析其邊界條件的施加以及扭轉中心的獲取，通過仿真計算以及試驗得到軸系強迫振動結果并進行了對比，得出了以下結論：

1）采用有限元方法對半拐剛度進行計算，其邊界條件需與結構實際受力情況一致。

2）對半拐剛度計算結果分析發現，具有彈性的半拐部件在受到扭矩的情況下，扭轉中心不會產生于主軸頸軸線上，而是會發生偏移，會影響到對扭轉剛度的計算。

3）三維扭振模態分析結果可以較好地用來快速校核集總參數模型的置信度。

4）發動機軸系扭振臺架試驗和相應的扭振仿真分析相互對比結果表明，相對于其他方法，基于準確的扭轉中心半拐剛度計算法能夠獲得更好的計算精度，更有利于準確的軸系扭振計算及減振效果分析。