永磁超環面電機模糊終端滑模的直接轉矩控制

劉 欣， 王佳奇

(天津工業大學天津市現代機電裝備技術重點實驗室， 天津, 300387)

近年來，集成電機技術迅速發展，由于其大轉矩、高效率以及高可靠性等優點在工業生產中得到了廣泛的應用[1-2]。永磁超環面電機是一種新型的集成電機，它結合了永磁同步電機與行星輪蝸桿傳動，具有定子到轉子的減速功能，實現了電磁動力裝置和減速機構的完美結合，具有結構緊湊與傳遞效率高的優點，在車輛、軍事以及航空航天等空間利用率較高的領域具有廣闊的應用前景[3-6]。

國內外對永磁超環面電機的研究主要集中于電磁特性的分析和電機結構的優化[7-9]。文獻[10]中使用新型指數趨近律的滑模控制策略對永磁超環面電機進行控制，解決了傳統指數趨近律滑模增益選取難的問題，并且縮短了穩態時間，增強了魯棒性，但是存在抖振問題。文獻[11]在內模控制與雙閉環控制相結合的基礎上加入了模糊控制，與傳統雙閉環控制系統相比，響應速度、超調量以及轉矩波動等性能都有明顯的優勢，但是由于實際生產條件與理論研究有較大偏差，理想內模控制的實現較為困難。

永磁超環面電機由于結構和行星輪自轉的影響，使輸出轉速與電磁轉矩具有較大的波動，過大的輸出波動易給傳動精度帶來不良影響，因此設計有效的控制器減小輸出波動尤為重要。滑模控制器對數學模型精度要求不高并且具有抗干擾能力[12]，可以解決永磁超環面電機數學模型的精度以及外部干擾對控制系統參數產生影響等問題。模糊控制可以在線調節滑模控制器參數。文獻[13]將滑模控制器與模糊控制相結合應用于永磁同步電機中，提高了系統動靜態性能，減小了電磁轉矩的脈動。

1 結構原理和波動特性分析

永磁超環面電機的結構示意圖如圖1所示，主要組成為：1環面蝸桿內定子、2行星輪、3環面外定子、4行星架轉子。內定子外環面上均勻分布空間螺旋的電樞槽，槽內安放著電樞線圈，形成電樞繞組。在環面蝸桿內定子與環面外定子之間均勻安裝著行星輪，在行星輪上均勻鑲嵌著永磁齒。永磁超環面電機電樞繞組接通三相交流電，在環面蝸桿內定子表面形成空間螺旋的旋轉磁場，旋轉磁場對行星輪產生沿著行星輪表面的一個切向作用力和一個軸向作用力，切向作用力使行星輪自轉，軸向作用力使行星輪公轉。環面外定子產生與旋轉磁場作用力大小相等、方向相反的作用力，2個作用力相互平衡，使行星輪平穩地進行公轉和自轉。行星輪的中心軸都與行星架連接，行星輪的公轉帶動行星架的轉動。

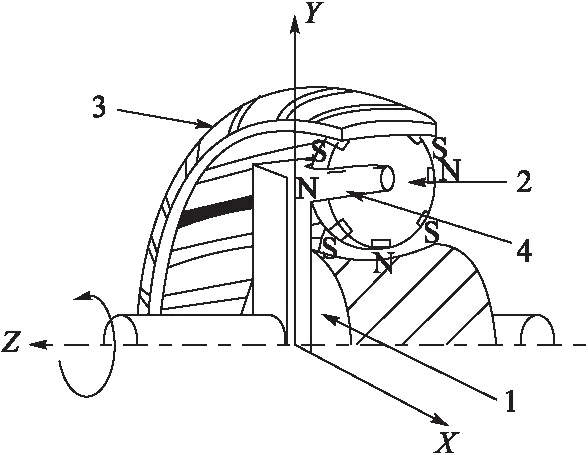
圖1 超環面電機結構示意圖

圖2為蝸桿繞組與行星輪永磁齒的嚙合關系，當蝸桿繞組通入三相交流電時，會產生磁鏈，行星輪周期性公轉和自轉引起磁鏈對應的電感發生變化，以其中一相繞組為例，對A1電流元進行分析，把它分解為一個沿行星輪切線方向即行星輪自轉方向的電流i1和一個沿蝸桿切線方向即行星輪公轉方向的電流i2，分別取2個分量進行分析，根據雙反應理論將i1產生的磁動勢幅值分解到直軸和交軸上，聯立單位面積氣隙磁導可得到直軸和交軸上的基波磁感應強度，于是可得到基波氣隙磁場和漏磁場所產生的自感磁鏈，進而得到i1產生的自感方程為：

LAA1=Ls0+Ls2cos(2θ)

(1)

同理可得到i2作用下產生自感方程為：

LAA2=Ls0+Ls2cos(2θ2)

(2)

式中：LAA1為由i1產生的A相定子繞組自感；LAA2為由i2產生的A相定子繞組自感；Ls0為永磁超環面電機A相定子繞組自感平均值；Ls2為永磁超環面電機A相定子繞組自感二次諧波的幅值；θ為行星輪公轉的電角度；θ2為行星輪自轉的電角度。

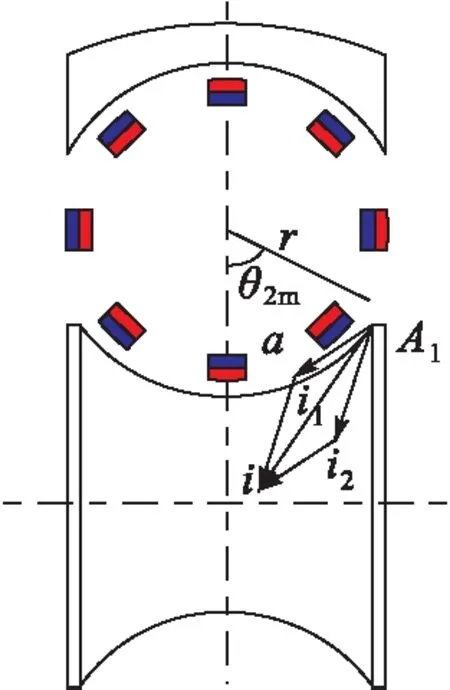
圖2 蝸桿繞組與行星輪永磁體嚙合關系

為了統一變量，結合永磁超環面電機的傳動特性可得到行星輪公轉電角度與行星輪自轉電角度的關系，此關系表示為運動參數k：

(3)

式中：θm為行星架轉子機械角度；θ2m為行星輪自轉機械角度；ωe為行星架轉子的電角速度；ω2為行星輪自轉的電角速度；np為蝸桿內定子的極對數；np2為行星輪的極對數。根據轉化機構法，給永磁超環面電機傳動系統加上虛擬角速度-ωe，可得到行星輪自轉方向到環面外定子的傳動比為：

(4)

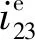
(5)

將i2產生的自感的影響加入到i1產生的自感中，即i1和i2產生的2個電感的合成，合成后的電感為：

(6)

式中：r為行星輪半徑；a為行星輪與蝸桿內定子的中心距。為了化簡電感方程，可引入表示蝸桿內定子與行星輪尺寸關系的結構參數m：

(7)

把結構參數m代入式(6)可得到永磁超環面電機A相繞組的電感方程為：

LAA(θ)=Ls0+Ls2(1-mcos(2kθ))cos(2θ)

(8)

永磁超環面電機環面蝸桿內定子繞組電感一個周期內的電感如圖3所示。

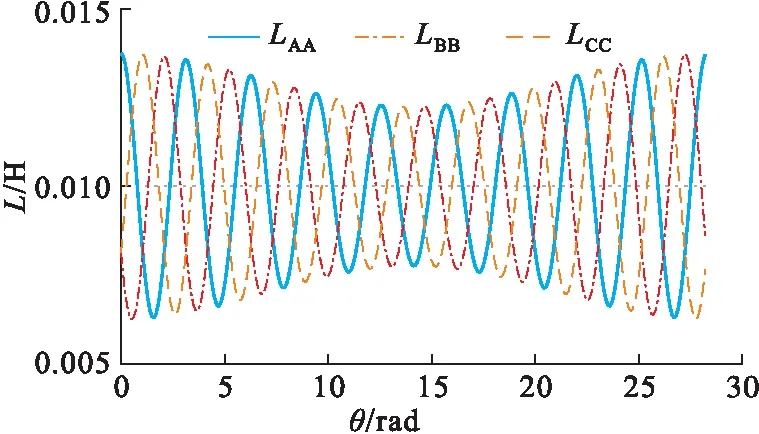
圖3 永磁超環面電機蝸桿繞組電感

蝸桿繞組電感在一個大周期內含有1/k個小周期。行星輪永磁齒產生的勵磁磁勢等效為勵磁線圈通虛擬勵磁電流If產生，且If恒定。行星輪在蝸桿內定子的包角范圍內進行電磁嚙合，由于行星輪的公轉的同時發生自轉，行星輪參與嚙合的永磁齒數量發生周期性變化，因此使行星輪永磁齒產生的磁鏈發生周期性變化，經分析可得到行星輪永磁齒磁鏈方程為：

ψfA(θ)=If[Ls0+Ls2(1-mcos(2kθ))]cosθ

(9)

式中：ψfA為行星輪永磁齒磁鏈。由蝸桿內定子三相繞組對稱性可得到行星輪永磁齒的磁鏈，由于磁鏈和電感的周期性變化導致輸出轉速和電磁轉矩具有周期性波動，為了對電機進行針對性的控制，減小輸出轉速和電磁轉矩的波動顯得尤為重要。

2 數學模型和動態特性分析

不計渦流磁滯損耗以及鐵心飽和效應，建立永磁超環面電機的數學模型，蝸桿內定子d、q軸磁鏈方程為：

(10)

式中：Ld(θ)、Lq(θ)分別為d、q軸電感。電流方程為：

(11)

式中：β為蝸桿內定子A相電流電角度；Ima為蝸桿內定子繞組三相電流幅值。電壓方程為：

(12)

式中：ud、uq分別為d、q軸電壓；id、iq分別為d、q軸電流；R為蝸桿內定子電阻；ψd(θ)為蝸桿內定子d軸的磁鏈；ψq(θ)為蝸桿內定子q軸的磁鏈。根據機電能量轉換原理，通過磁場儲能對行星架轉子角位移的偏導數可得靜止坐標系下的電磁轉矩方程，結合d、q坐標系下磁鏈方程和電流方程可得d、q坐標系下的電磁轉矩方程和運動方程為：

(13)

(14)

式中：TL為負載轉矩；J為轉動慣量；B為摩擦系數。

為了得知永磁超環面電機電磁轉矩和輸出轉速從起動到穩態的變化情況，需要對其動態特性進行分析。使用狀態空間分析法中的數學模型表示法，得到其動態方程為：

(15)

根據式(15)，可對永磁超環面電機進行動態特性分析，其中電機參數有m=0.4、k=1/9、R=8 Ω、Ls2=0.003 H、J=0.08 kg·m2、B=0.02 kg·m2/s、np=4、If=50 A，得到動態響應曲線如圖4和圖5所示。

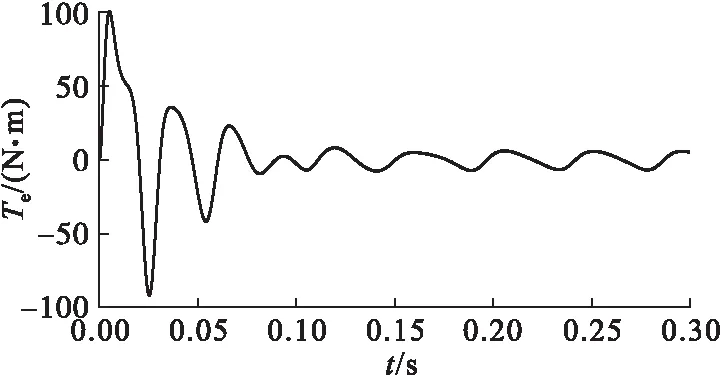
圖5 永磁超環面電機電磁轉矩

由圖4和圖5可以看出永磁超環面電機在空載起動時在瞬態調整過程初期輸出轉速會產生沖擊。起動階段轉速的超調量為44%，達到穩態的時間為0.1 s。穩態后輸出轉速具有周期性波動，輸出轉速范圍為705～787 r/min，波動幅度為82 r/min。電磁轉矩在調整階段產生較大的沖擊，穩態后產生周期性波動，電磁轉矩范圍為-7.1～6.2 N·m，波動幅度為13.3 N·m。

3 控制器設計

3.1 磁鏈環和轉矩環的super-twisting滑模控制器設計

本文在磁鏈環和轉矩環使用2個super-twisting滑模控制器代替滯環控制器，super-twisting算法可以表示為：

(16)

式(16)控制算法不需要對滑模變量s求導，在滑模面上收斂且穩定的充分必要條件為[14]：

Kp>AM/Bm

(17)

式中：AM為控制器輸出量二階導數上限絕對值的最大值，BM、Bm分別為控制器輸出量二階導數下限的最大值和最小值。

為了獲得磁鏈環、轉矩環控制器表達式，分別定義磁鏈、轉矩滑模變量為：

(18)

super-twisting滑模的趨近律中的開關函數在原點附近存在不連續性，會造成電磁轉矩和輸出轉速的脈動問題，所以使用連續且光滑的雙曲正切函數代替開關函數，根據super-twisting算法的二階滑模基本原理，此時永磁超環面電機控制系統中磁鏈環與轉矩環控制器的表達式分別為：

(19)

(20)

式(19)和式(20)設計的控制器由3部分組成，第1部分為冪次趨近率，主要影響控制速度。第2部分為滑模變量的積分函數，主要影響控制精度，第3部分為擾動部分。其中Kp1>0、Kp2>0、Ki1>0、Ki2>0，r1、r2為待設計參數，且0≤r≤0.5。永磁超環面電機特殊結構以及行星輪自轉產生擾動量為：

f=2nprLso/a(z2+z3)

(21)

3.2 轉速環終端滑模控制器設計

選用終端滑模控制器對轉速進行控制，定義狀態誤差為：

(22)

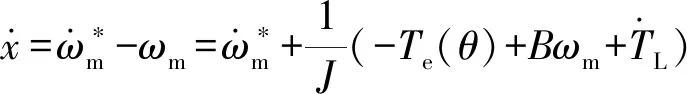
(23)

定義終端滑模面函數為：

(24)

對于式(24)轉速誤差系統，設計如下轉矩的控制率：

(25)

(26)

(27)

式中：k1、k2、k3、β、p、q為待設計參數,k1>J/TL；Ted是對滑模運動的趨近運動階段進行控制；Ten是對滑模面附近并沿著滑模面運動時進行控制。

取李雅普諾夫函數V=0.5s2對式(26)控制器進行穩定性證明：

(28)

當k2≥0、k3≥0時，可以證明轉速環終端滑模控制器的穩定性。

3.3 轉速環模糊終端滑模控制器設計

終端滑模控制中一個關鍵的問題就是存在抖振現象，在轉速環的控制器設計中，結構參數m和運動參數k可以看作控制器參數且由分析可知在m、k可取值的范圍內，取較大的值時輸出波動較小，所以當輸出轉速波動增大時可以通過對速度環終端滑模控制器中的m、k進行調節來減小輸出波動，但是取值過大會影響系統的響應速度，因此在轉速環的終端滑模控制器中設計模糊控制器，輸入為轉速的誤差值x，輸出為m、k的調節值。使用模糊控制器對m、k進行整定，減小輸出轉速與電磁轉矩的波動，又可以得到較快的響應速度。模糊終端滑模控制率設計如下：

(29)

式中：Δm、Δk為2個模糊控制器的輸出量，即m、k的調節后的增量。根據不同的輸入，選擇不同的輸出，將x、m、k分別分為7個等級，根據模糊滑模控制原理定義如下：

x(Δm)(Δk)={NB NM NS ZO PS PM PB}

當輸出轉速的誤差x較大時取較大的m、k以減小輸出轉速的波動。當x較小時，為了增快系統響應速度需要減小m、k。根據上述分析可以制定以下模糊規則表1。

表1 模糊規則表

輸入量x,輸出量Δm和Δk的隸屬度函數如圖6～8所示。利用重心法進行反模糊化，確定具體的參數值。

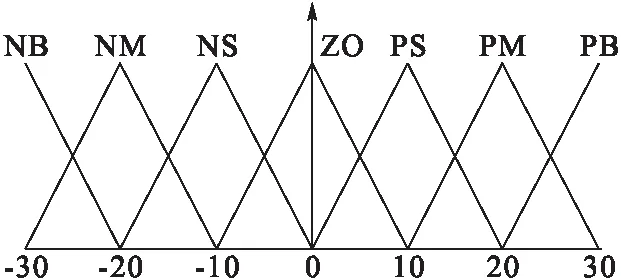
圖6 x的隸屬度函數

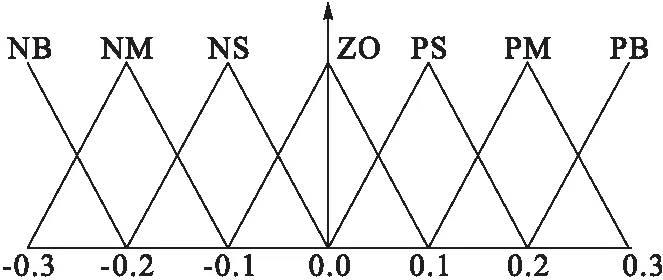
圖7 Δm的隸屬度函數

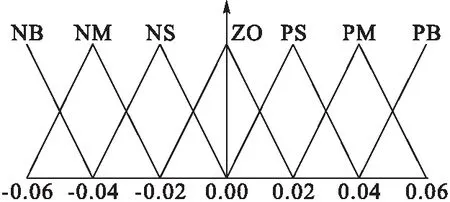
圖8 Δk的隸屬度函數

4 仿真分析

根據本文的理論分析可設計永磁超環面電機模糊終端滑模的直接轉矩控制策略，控制系統框圖見圖9，模糊終端滑模控制器框圖見圖10。

圖9 控制系統框圖

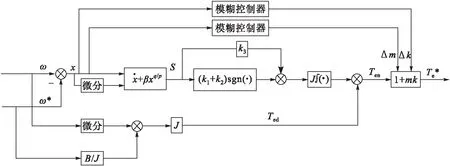
圖10 模糊終端滑模控制器框圖

由圖9～10可對永磁超環面電機控制系統進行分析，通過矢量脈寬調制技術作用于逆變器產生三相電壓，整個控制系統使用雙閉環反饋控制，在外環的轉速環使用模糊終端滑模控制器，輸入轉速的誤差，輸出參考轉矩。結合直接轉矩控制在內環的轉矩環和磁鏈環分別使用super-twisting滑模控制器，分別輸入轉矩和磁鏈的誤差，輸出為d、q軸的電壓，通過3個控制器共同對永磁超環面電機進行控制。

為了驗證該控制策略的有效性，建立了永磁超環面電機模糊終端滑模的直接轉矩控制的仿真模型，轉速環分別使用終端滑模控制器以及模糊終端滑模控制器進行仿真對比。模糊滑模控制器參數為β=100、p=9、q=7、k1=600、k2=300、k3=2 500。Super-twisting控制器參數為r=0.5、Kp1=100、Ki1=1、Kp2=100、Ki2=1。仿真結果見圖11～16。

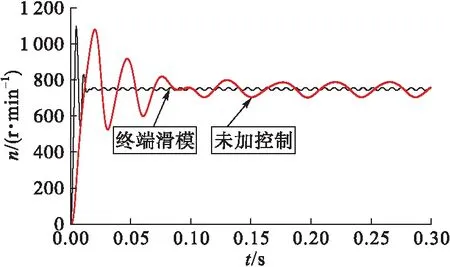
圖11 未加控制與終端滑模輸出轉速對比

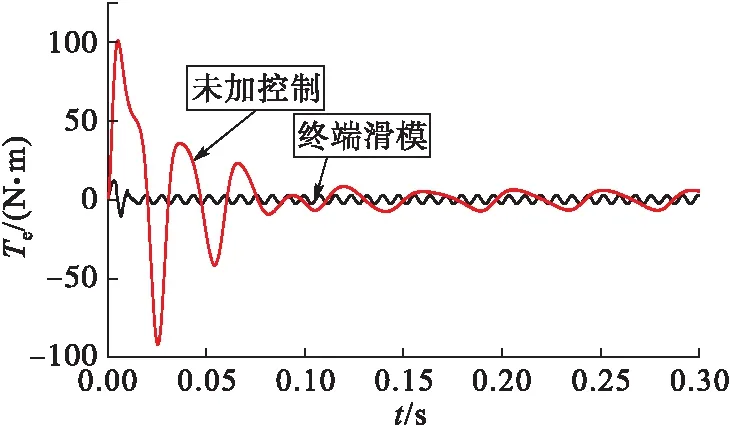
圖12 未加控制與終端滑模電磁轉矩對比

圖11和圖12為永磁超環面電機終端滑模的直接轉矩控制與未加控制策略的響應對比，可知控制后達到穩態的時間為0.02 s，比未加控制時的時間縮短了80%，具有更快速的動態響應性能。達到穩態后電機輸出轉速產生周期性波動，波動范圍為740～758 r/min，比未加控制時減小了78%。因此該控制策略能極大地改善輸出轉速的波動情況。電磁轉矩在達到穩態前的最大沖擊為12 N·m，穩定后波動范圍為-2.6～2.6 N·m，波動幅度為5.2 N·m，比未加控制減小了61%。

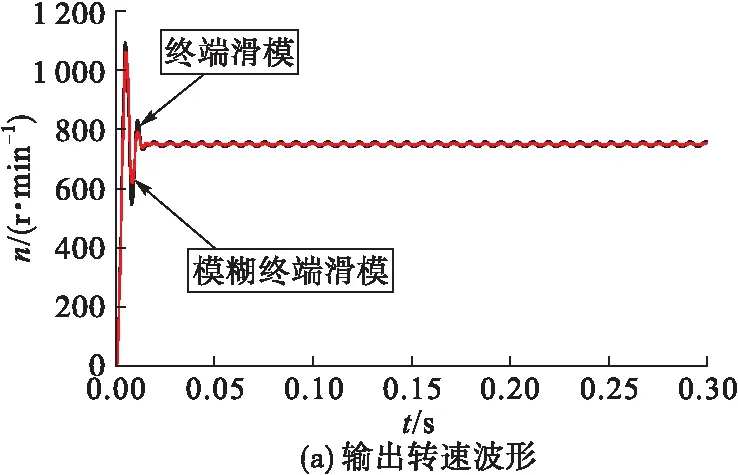
圖13 終端滑模與模糊終端滑模輸出轉速對比

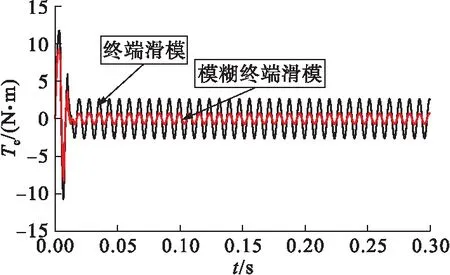
圖14 終端滑模與模糊終端滑模電磁轉矩對比

圖13和圖14為永磁超環面電機模糊終端滑模的直接轉矩控制與終端滑模的直接轉矩控制的響應對比，可知前者的輸出轉速在調整階段超調量為38%，比未加控制以及使用終端滑模時減小了6%，輸出轉速的超調得到了一定程度的抑制，達到穩態后輸出轉速產生周期性波動，但波動范圍進一步減小，其波動范圍為746～754 r/min，波動幅度為8 r/min，比使用終端滑模控制時減小了55.6%，輸出轉速的波動情況進一步改善。電磁轉矩在達到穩態前的最大沖擊為9.2 N·m，比使用終端滑模時減小23.3%。穩定后波動范圍-0.7～0.7 N·m，波動幅度為1.4 N·m，比使用終端滑模時減小73%，因此終端滑模控制結合模糊控制后可以使永磁超環面電機更穩定地進行轉矩輸出。

圖15和圖16為永磁超環面電機模糊終端滑模的直接轉矩控制在0.15 s時突加TL=2.5 N·m的負載轉矩時的響應，可知在外加干擾的情況下，永磁超環面電機也能快速恢復到給定的的轉速值，并且電磁轉矩在0.15 s時發生突變，最終穩定在2.5 N·m，因此該控制策略對外加干擾具有魯棒性。

圖15 模糊終端滑模突加負載時輸出轉速

圖16 模糊終端滑模突加負載時電磁轉矩

5 結語

本文根據永磁超環面電機的結構特點和行星輪周期性運轉的運動特性，推導了周期性變化的電磁參數，建立了該電機的數學模型并進行了動態特性分析。在控制系統內環的super-twisting滑模控制器中加入了與電機參數有關的擾動量。針對該電機輸出的周期性波動，在外環的轉速環設計了以該電機結構參數與運動參數增量調節控制器參數的模糊終端滑模控制器。仿真實驗表明，此控制策略有效地提高了永磁超環面電機系統響應速度，減小了輸出轉速與電磁轉矩的波動，并且還對外加干擾具有較強的魯棒性能。