MW級空間核反應堆系統熱管式輻射散熱器分析及優化

張昊春，劉秀婷，魏前明，游爾勝，孫銘遠

(1.哈爾濱工業大學 能源科學與工程學院，黑龍江 哈爾濱 150001；2.中國核動力研究設計院 中核核反應堆熱工水力技術重點實驗室，四川 成都 610213)

空間核動力系統因其輸出功率高、能量密度大、工作時間長[1]成為深空探測最具發展前景的選擇之一。由于大功率空間核反應堆系統需要大量散熱，故其輻射散熱部分體積通常占據整體的60%左右，因此，對大功率空間核反應堆系統的輻射散熱器進行設計和分析優化具有實際意義和參考價值。

已有的熱管式空間冷卻堆熱電轉換系統皆為概念設計方案，主要是堆芯熱管所選用的工質和熱電轉化方式不同。如采用鋰熱管冷卻堆芯、分段式靜態熱電偶轉換器進行熱電轉換的HP-STMCs[2]和采用鈉熱管冷卻堆芯、堿金屬熱電轉換裝置(AMTEC)進行熱電轉換的SAIRS[3](scalable AMTEC intergraded reactor space power system)熱管式空間冷卻堆，以上兩種系統均采用鉀熱管通過散熱器將廢熱排向太空。此外，還有用于火星表面活動的電源、熱量通過鈉熱管被帶出堆芯傳遞到能量轉化系統的HOMER[4](heatpipe-operated mars exploration reactor)，通過自由活塞式斯特林發電機實現熱電轉換的kW級空間核反應堆電源Kilopower等[5]。近年來熱管式輻射散熱器的性能研究是國內外研究熱點，謝榮建[6]運用遺傳算法對地球靜止軌道熱控系統中熱管輻射散熱器進行性能研究，得出了熱控制要求下最輕的散熱器質量。劉逍等[7]對空間堆熱管式輻射散熱器進行初步設計分析，得到了相應功率下，必要熱管根數及最佳冷卻流體流量。Jebrail等[8]對熱管式熱電偶散熱器進行了研究。Bieger[9]對微重力環境下的熱管長度、厚度參數進行優化設計，在滿足熱管散熱功率的條件下，得出其設計熱管的最佳參數。Sam等[10]提出一種應用于實際工程設計的熱管式散熱器的優化，考慮到功率最大的狀態、太陽能通量、散熱和元件的設計溫度上限，確定最佳散熱器的尺寸。Wenwen等[11]為俄羅斯TOPAZ-Ⅱ空間核電源系統提出了一種堿金屬熱管式散熱器，采用以鉀為工質的高溫熱管，絲網作為芯層，采用不銹鋼制成，通過輻射散熱，選擇整體碳翅片覆蓋和連接熱管作為整個輻射散熱器。本文基于熱管式散熱器的工作原理，通過遺傳算法，獲得多因素下散熱器質量的最優解，以降低空間核反應堆的運行負荷。

1 工作原理

圖1 空間熱管式輻射散熱系統示意圖

熱管式空間輻射散熱器由多個熱管式輻射散熱器單元組成，其工作流程為：流動的冷卻劑工質從熱源吸收經熱電轉換后的廢熱，在冷卻劑工質流經輻射散熱器時，熱量被傳遞至輻射散熱器，輻射散熱器上安裝熱管，熱量經熱管傳遞給輻射翅片，輻射翅片底部加裝隔熱層，屏蔽熱量向航天器的輻射，熱量最后通過輻射排向外太空。圖1為空間熱管式輻射散熱系統示意圖。熱管管殼材料選取高強度質量比、高導熱率的鎳合金，工作介質選擇熔點為98 ℃、沸點為892 ℃的液態金屬鈉[12]，其工作溫度為600～1 200 ℃，熱管吸液芯材料選擇鉬錸合金(Mo-14%Re)[13]，熱管與裸碳纖維翅片焊接選用導熱系數為219 W/(m·K)的活性釬焊合金Ticusil[14]，熱管冷凝段釬焊連接裸碳纖維翅片[15]。冷卻劑回路工作介質選擇液態金屬鉀，其物性參數參見文獻[16-17]。熱管的工作原理如圖2所示。典型的熱管由熱管外殼、緊貼內壁的吸液芯毛細多孔材料、端蓋構成。熱管被加熱的一端稱為蒸發段，熱量經熱管壁傳遞給吸液芯(多孔材料)，再傳遞給吸液芯中的液態工作介質使之蒸發氣化，該熱量即為液態工作介質的蒸發潛熱，由于熱管蒸發段蒸氣溫度高所引起的壓力差驅動蒸氣從中心氣腔流向熱管另一端，高溫蒸氣在另一端遇冷凝結，同時釋放出潛熱，這一端被稱為冷凝段。熱管冷凝段冷凝的飽和液體由于受到管芯多孔材料的毛細力重新流回蒸發段。如此循環往復，熱量便由熱管一端傳遞至另一端。

圖2 熱管工作原理示意圖

2 參數選擇和模型建立

2.1 主要設計參數

參考輻射散熱器的經典參數，對于MW級空間核電源，堆芯功率為3.2 MW，轉換效率為31.8%，廢熱排出要求為2.18 MW[15]。輻射散熱器進口溫度為800 K，冷卻劑回路質量流量為8 kg/s，冷卻劑回路管道直徑為50 mm。輻射散熱器中熱管的尺寸參數列于表1。

表1 輻射散熱器熱管設計參數

冷卻劑回路工作介質可選擇液態金屬鉀(臨界溫度2 222 K，臨界壓力16.2 MPa)，鉀物性參數可由式(1)～(4)計算。

λ=92.95-0.058 1T+11.727 4×10-6T2

(1)

cp=1 436.72-0.580T+4.627×10-4T2

(2)

lnμ=-6.484 6-0.429 03lnT+485.3/T

(3)

ρ×10-3=0.902 813 76-0.169 907 11×

(T×10-3)-0.268 647 69(T×10-3)2-

0.505 681 88(T×10-3)3-0.465 379 12×

(T×10-3)4+0.203 781 07(T×10-3)5-

0.034 771 31(T×10-3)6

(4)

式中：ρ為液體密度，kg/m3；λ為導熱系數，W/(m·K)；cp為比定壓熱容，kJ/(kg·K)；T為溫度，K；μ為動力黏度，Pa·s。

2.2 換熱計算

1) 熱管式輻射散熱器與宇宙空間輻射散熱

當MW級空間輻射散熱器正常工作時，熱量來源為冷卻劑溫降，熱量去向為空間環境的輻射散熱，選取第i個熱管式輻射散熱器單元作為研究對象，熱管式輻射散熱器單元由單根熱管、加裝在熱管兩側的裸碳纖維翅片組成。由于MW級航天飛行器處于深空宇宙，無對流換熱，考慮到熱管的等溫性，將三維翅片沿熱管方向簡化成單位長度的二維翅片模型，如圖3所示。

圖3 二維翅片輻射散熱模型

記翅長(相鄰熱管間距)為Lf、翅厚δf、翅根溫度為Tr。以翅根與翅片下端絕熱層的交點為坐標原點建立直角坐標系。x在0～Lf之間取值，y在0～δf之間取值，n為節點個數。

二維模型內部節點控制方程[18]如下：

?2T/?x2+?2T/?y2=0

(5)

上邊界：

λT(i,ny)=λT(i,ny-1)-

(6)

式中：ε為發射率；σ為輻射常數，W/(m2·K2)。

運用有限差分和迭代法，可計算二維翅片模型穩態熱分布，通過迭代計算可得出單位翅長輻射面各點的溫度。求得輻射面各點溫度后，可由式(7)計算熱管式輻射散熱器單元的輻射散熱量。

(7)

2) 熱管式輻射散熱器的單元流體換熱計算

熱量由冷卻劑傳遞到熱管蒸發段外壁的過程中，換熱熱阻分為兩部分：(1) 冷卻劑與冷卻劑管道的對流換熱；(2) 熱量由冷卻劑管內壁傳遞到冷卻劑管外壁。則該過程總的換熱熱阻R1[19]為：

(8)

式中：din、dout、lp和tp分別為冷卻劑管道內徑、外徑、長度和厚度，m；λcp為冷卻劑管道管壁徑向導熱系數，W/(m·K)；hc為冷卻劑管道管內換熱系數，W/(m2·K)。

再考慮熱量由熱管蒸發段外壁傳遞至裸碳纖維翅片翅根處的換熱熱阻R2。

R2=Rhpv+Rhpc+R0

(9)

設熱量從熱管蒸發段管壁外部傳到熱管蒸發段內表面過程中沿管壁徑向的導熱熱阻為Rhpv，則有：

(10)

式中：dhpvi、dhpvo和thpv分別為熱管蒸發段內徑、外徑和管壁厚度，m；λhp為熱管管材徑向導熱系數，W/(m·K)。

熱管吸液芯管芯的結構選擇流動阻力小、毛細力大的干線芯管芯，熱管沿管徑方向的熱阻很小，且由于熱管沿軸向的等溫性，則可忽略熱管工質從熱管蒸發段到冷凝段的換熱熱阻。設熱量從熱管冷凝段管壁內部傳到冷凝段外表面過程中沿管壁徑向的導熱熱阻為Rhpc，則有：

(11)

式中，dhpci、dhpco分別為熱管冷凝段內徑、外徑，m。

設熱量通過熱管冷凝段外壁與翅片連接的釬焊層的導熱熱阻為R0，則：

(12)

式中：λ0為釬焊層材料徑向導熱系數，W/(m·K)；t0為釬焊層厚度，m。

則冷卻劑傳遞到裸碳纖維翅片翅根總換熱熱阻R可由下式計算：

R=R1+R2

(13)

3) 熱管式輻射散熱器系統熱分析

已知熱管式輻射散熱器冷卻劑入口溫度Tf1,1及總設計散熱功率Q0，采用迭代法從第1個熱管式輻射散熱器單元開始計算，對熱管式輻射散熱器系統進行熱分析。

假設第i個熱管式輻射散熱器單元冷卻劑出口溫度為Tf2,1，根據式(14)可計算熱管式輻射散熱器單元單位時間內從冷卻劑吸收的熱量Qi，由式(5)可計算裸碳纖維翅片翅根溫度Tr，進而由式(7)可求得熱管式輻射散熱器單元的輻射散熱量QR,i。

Qi=cpm(Tf1,i-Tf2,i)

(14)

A=N(2Lf+do)lhpc

(15)

M=2NLflhpcδfρfin+

(16)

式中：ρfin為裸碳纖維翅片密度，kg/m3；ρhp為熱管材料密度，kg/m3。

3 分析及優化

3.1 熱管式輻射散熱器質量影響因素

選取冷卻劑質量流量m、裸碳纖維翅片長度Lf、裸碳纖維翅片厚度δf、熱管式輻射散熱器入口溫度Tf1為優化參數對熱管式輻射散熱器系統質量M進行優化。

1) 翅片厚度δf

選取Lf=5 cm、m=7 kg/s、Tf1=800 K，探討δf對M的影響，結果示于圖4。使用鉀作為冷卻劑，當δf由0.1 mm增加到0.9 mm時，M先減小后增大，當δf為0.2 mm時，M取得最小值972.9 kg。這是因為當δf過小時，由熱管傳遞至裸碳纖維翅片的熱量也很小，導致裸碳纖維翅片表面溫度過低，熱管式輻射散熱器單元輻射散熱量小，所需輻射單元數較多，故熱管式輻射散熱器系統總質量增加。

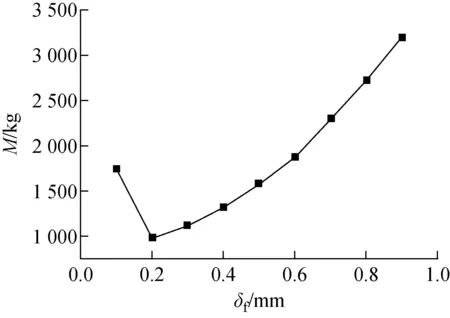
圖4 σf對M的影響

2) 翅片長度Lf

選取δf=0.2 mm、m=7 kg/s、Tf1=800 K，探討Lf對M的影響，結果示于圖5。從圖5可看出，當Lf從1.5 cm到9.5 cm變化時，熱管式輻射散熱器質量呈現先減小后增大的趨勢，當Lf為5 cm時熱管式輻射散熱器質量取得最小值972.9 kg。這是由于Lf增加到一定程度時，裸碳纖維翅片熱阻很大，外側表面溫度很低，導致其輻射能力變差。

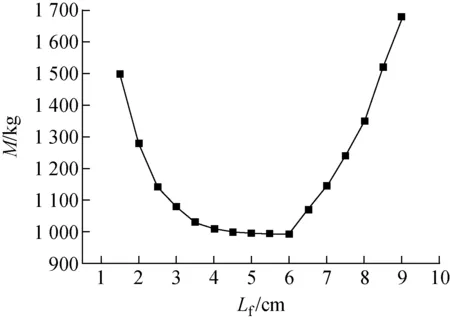
圖5 Lf對M的影響

3) 冷卻劑質量流量m

選取δf=0.2 mm、Lf=5 cm、Tf1=800 K，探討m對M的影響，結果示于圖6。當冷卻劑質量流量m增大時，熱量經由冷卻劑至裸碳纖維翅根的R越小，則Tr越大，進而裸碳纖維翅片輻射熱量越大，熱管式輻射散熱器系統質量越小。當質量流量大于9 kg/s時，熱管式輻射散熱器系統質量基本不變，考慮到泵功率不應超出核電源電功率的5%，且當質量流量大于9 kg/s時，熱管式輻射散熱器系統質量基本不變，則流量m取9 kg/s為宜。

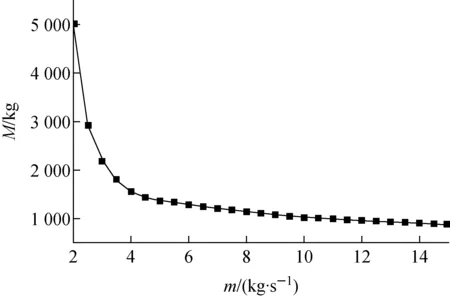
圖6 m對M的影響

4) 入口溫度Tf1

選取δf=0.2 mm、Lf=5 cm、m=7 kg/s，探討Tf1對M的影響，所得變化關系曲線如圖7所示。當熱管式輻射散熱器入口溫度Tf1增大時，Tr越大，裸碳纖維翅片輻射熱量越大，熱管式輻射散熱器系統質量M越小。但依靠增加熱管式輻射散熱器入口溫度Tf1來降低熱管式輻射散熱器系統質量制約因素很多，故結合前人設計經驗熱管式輻射散熱器入口溫度Tf1選擇800 K為宜。

圖7 Tf1對M的影響

3.2 遺傳算法對輻射散熱器質量的優化

1)Lf變化時輻射散熱器優化結果

在其他參數不變的情況下，選取裸碳纖維翅片長度Lf為4.5～5.5 cm，利用遺傳算法，設置初始種群數n為40、交叉率Pc為0.7、變異概率Pm為0.001 5、最大代數為150、代溝G為0.9，得到的最終優化結果如圖8所示。圖8表明，當Lf取5 cm時，M取得最小值912.10 kg。遺傳算法結果表明，當Lf取5.07 cm時，M取得最小值912.066 kg，此結果表明Lf在5 cm附近時M取得最小值。

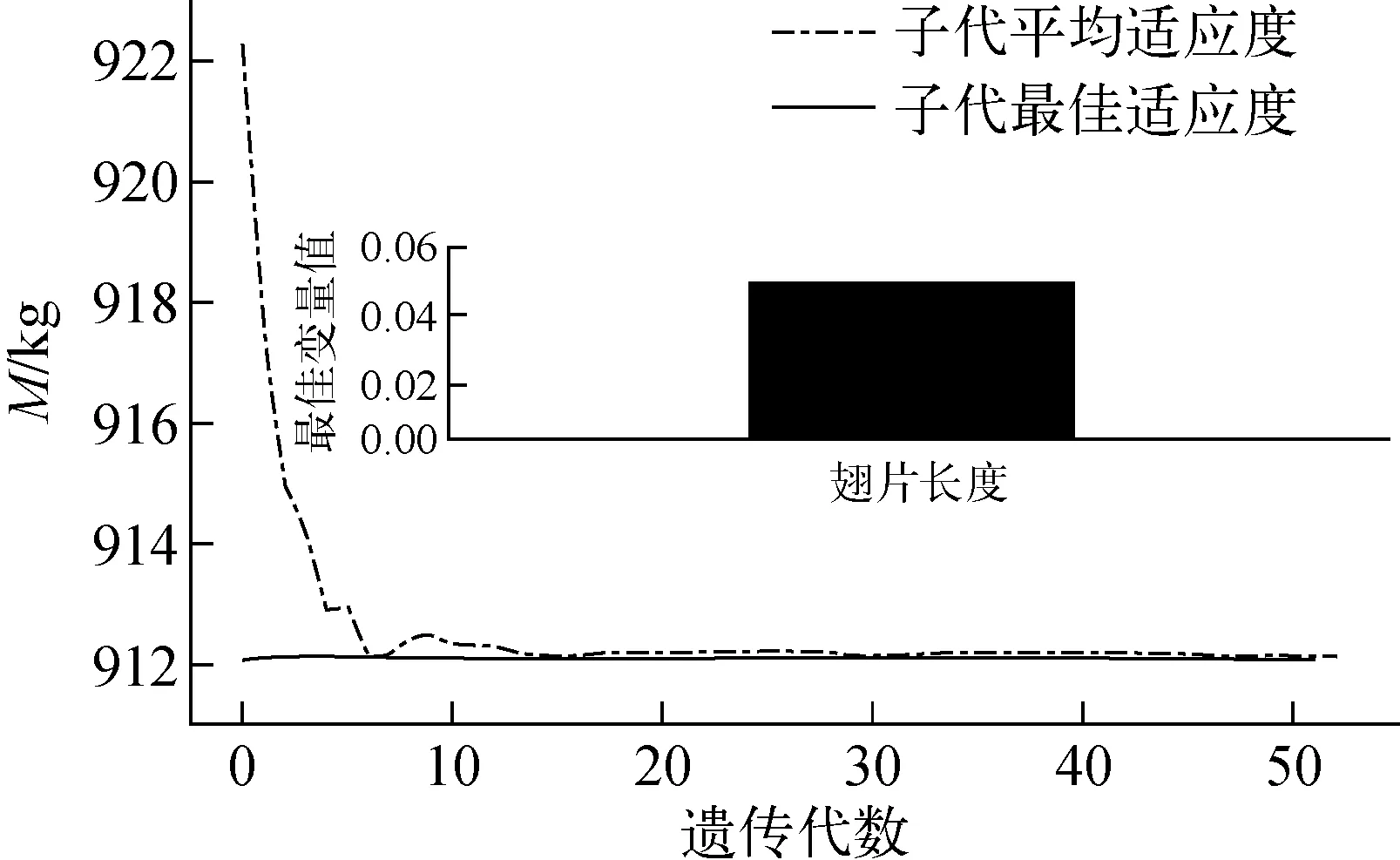
圖8 裸碳纖維翅片長度遺傳算法優化結果

2)δf變化時輻射散熱器優化結果

在其他參數不變的情況下，選取δf為0.1～0.2 mm，利用遺傳算法，設置遺傳算法參數如前文所述，得到優化結果如圖9所示。

圖9 裸碳纖維翅片厚度遺傳算法優化結果

圖9表明，當δf取0.16 mm時M取得最小值907.816 kg。為更好地探討輻射散熱器的質量優化和對比分析，采取多參數優化所得結果。

3) 多參數輻射散熱器質量優化

選取Lf為4.5～5.5 cm、δf為0.1～0.2 mm、m為6～9 kg/s、Tf1為400～800 K。設置遺傳算法運行參數，其中初始種群數n為40、編碼串長l為37、交叉率Pc為0.7、變異概率Pm為0.001 5、最大代數為150、代溝G為0.9。變量與目標函數M的遺傳算法如圖10所示。

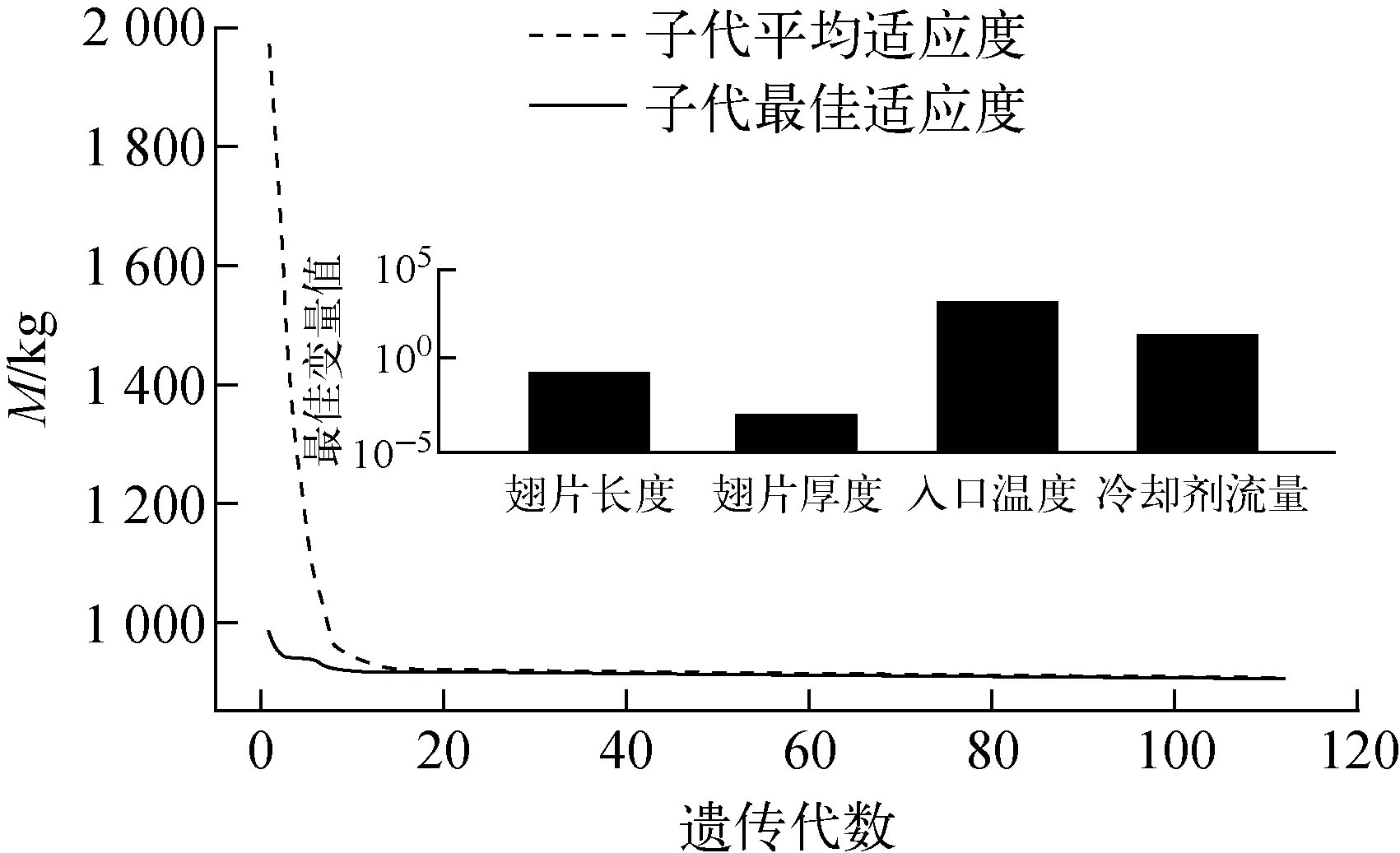
圖10 多變量遺傳算法優化結果

比較遺傳算法和窮舉法的結果可知：對于窮舉法，當Lf取5 cm、σf取0.2 mm時，M取得最小值912.10 kg；對于遺傳算法，當Lf取5.07 cm、δf取0.16 mm、Tf1取800 K、m取9 kg/s時，M取得最小值906.593 kg，優化了0.63%的系統質量。

4 結論

本文對MW級空間核反應堆系統的熱管式輻射散熱器進行了設計，并以輻射散熱器質量為優化目標，在遺傳算法的基礎上研究了冷卻劑質量流量m、裸碳纖維翅片長度Lf和厚度δf及輻射散熱器入口溫度Tf1對散熱器質量M的影響，得到以下結論：

1) 建立了熱管式輻射散熱器熱阻分析數學模型，計算得到了不同工況下輻射散熱器的系統質量，并給出了最優解；

2) 散熱器質量M隨質量流量m、入口溫度Tf1的增加而減小，取m為9 kg/s時可獲得較好優化結果；

3)M隨Lf和δf的增大呈先減小后增大的趨勢，Lf為5 cm和δf為0.2 mm時取得最小值972.9 kg；

4) 當Tf1=800 K、Lf=5 cm、δf=0.16 mm、m=9 kg/s時，M最小，此時M為906.593 kg，優化了0.63%的系統質量。