電網超低頻振蕩影響因素綜合分析與抑制措施研究

賀子潤，陳 振2，邢昊中

(1.輸配電裝備及系統安全與新技術國家重點實驗室(重慶大學)，重慶 400044；2.國網四川省電力公司電力科學研究院，四川 成都 610041)

0 引 言

2019年6月，西南電網與華中電網正式異步聯網運行，西南電網的水電占比高達70%以上，超低頻振蕩風險十分顯著。當發生超低頻振蕩時，系統內所有機組共同振蕩，頻率和功率也發生持續振蕩，突出特點是振蕩頻率低、振型特殊，所有機組轉速同調變化，無明顯的機間振蕩,是一種與傳統低頻振蕩機理完全不同的振蕩。

目前對于超低頻振蕩的研究主要從機理分析和控制措施方面開展研究。

1)在機理分析方面：文獻[1]在孤島系統中分析了水輪機調速器等參數對振蕩的影響。文獻[2]通過對大量試驗數據及水輪機調速器模型分析得出水電機組一次調頻是產生超低頻振蕩的直接原因。文獻[3]通過建立典型孤島送出系統，利用特征根分析和時域仿真方法對超低頻振蕩模式進行排查和分析；并通過靈敏度分析，研究了水輪機引水系統水錘效應時間常數、調速器參數對超低頻振蕩的影響。文獻[4]分別在單機系統研究了一次調頻過程不穩定導致的超低頻振蕩事件，研究超低頻振蕩的振蕩頻率、阻尼、振蕩表現等特征，并引入伯德圖方法分析詳細模型下的振蕩頻率和阻尼。文獻[5]進一步研究多機系統的超低頻振蕩的分析，并提出相應的等值方法。文獻[6]利用值集法提出了一套用于超低頻振蕩穩定分析的多參數圖形分析工具，并研究水輪機特性系數對穩定性的影響。文獻[7]利用復轉矩系數法研究了超低頻振蕩產生的機理以及水輪機調速器、汽輪機調速器、負荷模型和系統慣量對超低頻振蕩的影響，并將超低頻振蕩歸類為小干擾頻率穩定范疇。文獻[8]分析了水輪發電機調速系統對超低頻振蕩的影響及模型適用性問題。

2)在控制措施方面目前主要采用以下兩種措施：一是調整水電機組調速器參數，其優點是從源頭治理超低頻振蕩，并不影響水電消納。文獻[9-10]通過調整調速器PID參數大小實現超低頻振蕩的有效抑制，然而該方法的缺點是降低了水電調節速度，影響調頻能力。為解決此問題，文獻[11-12]同時考慮超低頻振蕩抑制和一次調頻性能的影響，建立調速器PID參數的優化模型，在抑制超低頻振蕩和維持調頻能力間取得平衡。二是直流附加控制措施。文獻[13]通過時域仿真，提出了直流附加頻率控制的參數設計原則。文獻[14]提出超低頻振蕩的多直流協調控制策略。利用直流進行控制的缺點是會將送端的擾動傳遞給受端，造成受端的功率波動，影響受端電網的安全穩定運行。

為綜合分析超低頻振蕩的影響因素并提出相應的控制措施，首先建立超低頻振蕩分析的單機帶負荷模型，并基于穩定域的思想綜合分析了電網超低頻振蕩的影響因素。在此基礎上，考慮水錘效應的不確定性，建立了調速器參數的優化模型，并提出優化模型的智能求解方法。

1 超低頻振蕩影響因素綜合分析

1.1 超低頻振蕩分析模型與方法

單機帶負荷系統是分析頻率穩定的最簡單系統，反映了系統發電和負荷之間的平衡及有功頻率控制的動態過程。基于單機帶負荷系統，分析系統發生超低頻振蕩的產生機理，其方框圖如圖1所示。

圖1 單機帶負荷系統

發電機的轉子運動方程：

(1)

式中：TJ為發電機慣性時間常數；Δω為發電機的轉速偏差；ΔPm為原動機的機械功率輸出偏差；ΔPe為發電機的電磁功率偏差；D為發電機的阻尼系數。

若忽略系統網損，僅考慮負荷的頻率變化，則有

ΔPL=ΔPe=KLΔω

(2)

式中：ΔPL為負荷的有功變化量；KL為負荷頻率調節效應系數。

由式(1)、式(2)可得發電機和負載的傳遞函數為

(3)

因D和KL的作用相同，可令Ds=D+KL。

水輪機的傳遞函數為

(4)

式中：Δμ為水輪機的導葉開度偏差；TW為水錘效應時間常數，其值隨負荷變化，滿載時TW取值為0.5～4.0 s。

目前，水輪機廣泛使用并聯型比例-積分-微分(proportion integration differentiation,PID)調速器進行調速，通過比例環節、積分環節、微分環節并聯共同控制水輪機的導葉開度，這里采用的并聯型PID調速器其傳遞函數為

(5)

式中：KP為調速器的比例系數；KI為調速器的積分系數；KD為調速器的微分系數；bP為調差系數；Ty為伺服系統時間常數。

通過上述傳遞函數，可以構造一個含水輪機調速器系統的單機帶負荷系統模型，用于分析超低頻振蕩的形成機理，其系統結構如圖2所示。

圖2 水輪機組成的單機帶負荷系統結構

超低頻振蕩分析方法主要包括復阻尼轉矩方法與特征根分析方法。前者利用復阻尼轉矩理論，將調速通道的阻尼轉矩分解為同步轉矩KmS和阻尼轉矩KmD。阻尼轉矩大于0，則表示調速通道提供正阻尼，否則提供負阻尼。阻尼轉矩絕對值的大小，表明調速通道提供正/負阻尼的大小。后者建立系統的傳遞函數，通過求解特征多項式的解判斷系統的穩定性，特征值實部大于0，表明系統失穩，否則表明系統穩定。

1.2 超低頻振蕩影響因素綜合分析

利用穩定域的思想，對影響超低頻振蕩的因素進行綜合分析。將各基本參數設置為：TJ=10 s，Ds=0.689，KP=0.5，KI=1.0，bP=0.04，Ty=0.2 s。分別設TW為0.5 s、0.7 s、0.9 s、1.1 s，在0～20范圍內改變KP、KI，對每一組參數，若求得的特征根實部為負數，即系統穩定時，在(KP，KI)平面上畫圈；若求得的特征根實部為正數，即系統不穩定時，在(KP，KI)平面上畫叉，由此得到不同TW下KP、KI對系統穩定性的影響分布圖，如圖3所示。

由圖3可知，當KP、KI一定時，增大TW，系統的穩定性顯著變差；當TW、KI一定時，增大KP，系統的穩定性先變好，再變差；當TW、KP一定時，增大KI，系統的穩定性變差。

2 考慮水錘效應不確定性的調速器參數優化模型與求解

2.1 考慮水錘效應不確定性的調速器參數優化模型

由前述分析可知，引起電網超低頻振蕩的一個重要原因是調速器參數設置不合理從而導致調速器產生負阻尼轉矩，通過優化調速器參數是抑制超低頻振蕩的一個有效手段。然而，現有致力于解決超低頻振蕩問題的水輪機調速器控制設計方法，更多地考慮了系統的穩定性，忽略了調速器需要承擔跟蹤負荷波動的任務，且調速器的穩定性與跟蹤性能直接存在矛盾。因此需要在優化調速器阻尼性能的同時，考慮到調速器的跟蹤性能。

另外，水錘效應時間常數TW也是影響水電為主電網超低頻振蕩的關鍵因素，其值的大小會隨著發電機出力的改變而改變。然而，現有的調速器優化模型中，往往忽略了TW的變化，認為其值為定值，導致參數優化結果難以適應運行狀態的改變。

為解決上述問題，根據歷史數據的統計結果，對TW在取值范圍內離散化處理，并得到確定各離散值對應概率的大小。這里假定TW離散概率分布如表1所示。

表1 TW的離散概率分布

另外，提出以誤差平方和時間乘積積分(integral time square error，ITSE)準則刻畫調速器的跟蹤性能，其表達式為

(6)

式中，ΔPm,i(t)為第i種工況下，水輪機輸入階躍響應后，輸入的時間響應與其穩態值之差。

在上述基礎上，建立調速器參數優化模型：

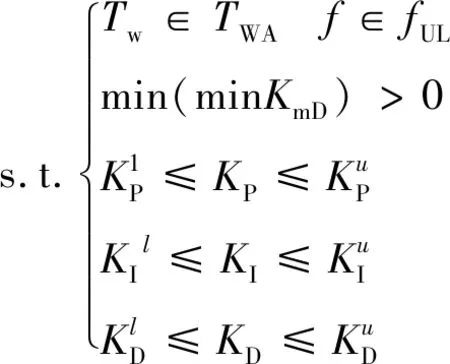
(7)

2.2 調速器優化模型求解

利用粒子群優化(particle swarm optimization,PSO)方法對上述參數優化模型求解，基于PSO的調速器參數優化模型的求解流程如圖4所示。

圖3各參數對超低頻振蕩穩定域的影響

圖4 調速器參數優化模型求解流程

3 算例驗證

對于超低頻振蕩問題，由于多機系統可以解耦成單機系統進行分析，因此以圖1所示的水輪機組單機帶負荷為例來驗證所提調速器參數優化算法的有效性。設定調速器的原始參數分別為KP=0.8、KI=1.2、KD=1.0。調速器參數的取值范圍均取為[0,5]，利用所提模型進行調速器參數優化，調速器參數分別為KP=5、KI=2.32、KD=5。

在4種不同TW取值下，參數優化前后水輪機-調速器通道在超低頻段的阻尼轉矩系數對比和參數優化前后的系統階躍響應曲線對比，分別如圖5、圖6所示。

由上述對比可知，所提方法能有效提升水輪機的阻尼系數，防止出現負阻尼的現象，從而避免系統發生超低頻失穩。另外，由于在優化模型中考慮了多種運行工況下的TW值，因此參數優化結果具有一定的魯棒性。

4 結 語

1)由超低頻振蕩影響因素綜合分析可知，當KP、KI一定時，增大TW，系統的穩定性顯著變差；當TW、KI一定時，增大KP，系統的穩定性先變好，再變差；當TW、KP一定時，增大KI，系統的穩定性變差。

2)考慮水錘效應不確定性的參數優化模型能有效抑制超低頻振蕩現象，并且具有一定的魯棒性。

圖5參數優化前后的阻尼系數對比

圖6參數優化前后的階躍響應對比