基于GIOWA算子的我國碳排放量的組合預測研究

陸玉玲

(安徽財經大學統計與應用數學學院，安徽蚌埠233030)

由于二氧化碳等溫室氣體的大量排放，氣候變暖問題已經成為當今時代面臨的一項重大挑戰，它對社會的健康可持續發展產生了重大的威脅。目前，我國是世界上最大的二氧化碳排放國，對碳排放進行科學準確地預測，有助于政府制定合理的碳減排政策，對推動我國生態文明建設和經濟高質量發展具有重要的作用。

針對碳排放預測研究，學者們主要采用兩類模型進行建模分析，分別是單一預測模型和組合預測模型。(1)單一預測模型。趙息等學者基于中國1980—2009年的碳排放數據，運用離散二階差分方程預測模型對碳排放進行預測[1]；鄧小樂和孫慧利用STIRPAT模型對西北五省區碳排放峰值進行了預測[2]；何永貴和于江浩基于河北省2003—2014年碳排放數據，運用灰色GM(1,1)預測模型對河北省2015—2020年碳排放量進行預測[3]；董聰等學者采用BP神經網絡對我國碳排放量進行預測[4]。(2)組合預測模型。肖枝洪和王明浩采用ARIMA模型與BP神經網絡集成的組合模型，對中國碳排放量進行預測研究，結果表明組合模型預測誤差較小[5]；Wang和Ye采用中國1953—2013年化石能源消費中的碳排放量數據，運用灰色模型、非線性灰色多變量模型和改進的非線性灰色多變量模型預測中國2020年的碳排放量，結果表明非線性灰色多變量模型具有最高的準確率[6]；劉炳春等學者基于主成分分析(PCA)和支持向量回歸(SVM)兩種方法構建組合預測模型對中國2016—2021年碳排放量進行預測，結果表明PCA-SVR組合模型誤差低于單項預測模型的誤差[7]。

本文選取中國1989—2018年間的碳排放量數據，在多元線性回歸、指數平滑和ARIMA(0,2,0)三種單項預測模型的基礎上，構建廣義誘導有序加權平均(GIOWA)組合預測模型對我國未來五年的碳排放量進行預測，為我國碳減排政策的制定提供一定的參考。本文的后續結構安排為：第一部分是建立單項預測模型對我國碳排放量進行預測；第二部分是建立基于GIOWA算子的組合預測模型對中國碳排放量進行預測；第三部分是根據單項預測模型和組合預測模型的碳排放量預測結果給出本文的結論。

1 全國碳排放量單項預測

1.1 多元線性回歸模型

選取城鎮化率(urbant/%：城鎮常住人口占總人口的比重)、能源消費強度(eit/噸標準煤/萬元：能源消費總量與國內生產總值GDP的比)、人均GDP(pgdpt/元/人)、產業結構(indt/%：第二產業增加值占GDP的比重)四個影響因素作為多元線性回歸模型的自變量，全國碳排放量(yt/百萬噸)作為模型的因變量，并將所有變量進行對數化處理以建立多元線性回歸模型。考慮到通貨膨脹因素的影響，GDP利用居民消費價格指數折算為1989年不變價。所有數據來源于《BP世界能源統計年鑒》、EPS全球統計數據庫和國家統計局。

運用逐步回歸法，得到如下多元線性回歸模型：

lnyt=-3.8686+0.2606lnurbant+1.0537lneit+0.9722lnpgdpt+0.4898lnindt+εt

(-19.4554) (4.2840) (36.9728) (45.1510) (12.6002)

(1)

1.2 Hlot-Winters 非季節指數平滑預測

對我國碳排放量進行對數化處理，運用Hlot-Winters 非季節指數平滑法，使用Eviews 7軟件計算得到阻尼因子為α=0.96和β=1，趨勢項為0.0216，截距項為9.1511，而預測出2019—2023年間各年的二氧化碳排放量。Hlot-Winters 非季節指數平滑方法的預測公式為：

(2)

式(2)中，T是待估計樣本的期末值[8]，k為T期到預測期的間隔期數。

1.3 自回歸移動平均ARIMA模型

首先，對中國碳排放量序列y進行對數化處理得到序列lny，經檢驗序列lny不平穩，然后，對lny進行差分處理，得到平穩的二階差分序列記為z，其自相關函數、偏自相關函數圖形如圖1所示。

圖1 zt序列的樣本自相關函數圖與偏相關函數圖

該序列在5%的顯著性水平下接近于一個白噪聲，因此可建立零階MA(0)模型[9]：

zt=εt

(3)

則對中國碳排放量對數序列lnyt可建立ARIMA(0,2,0)模型，即

lnyt=2lnyt-1-lnyt-2+εt

(4)

表1列出了多元線性回歸、Hlot-Winters 非季節指數平滑和ARIMA(0,2,0)三種單項預測模型的預測值和精度。由表1可知，同一單項預測模型在不同時點上的預測精高低是不相同的，因此有必要使用廣義誘導有序加權平均(GIOWA)的組合預測模型。

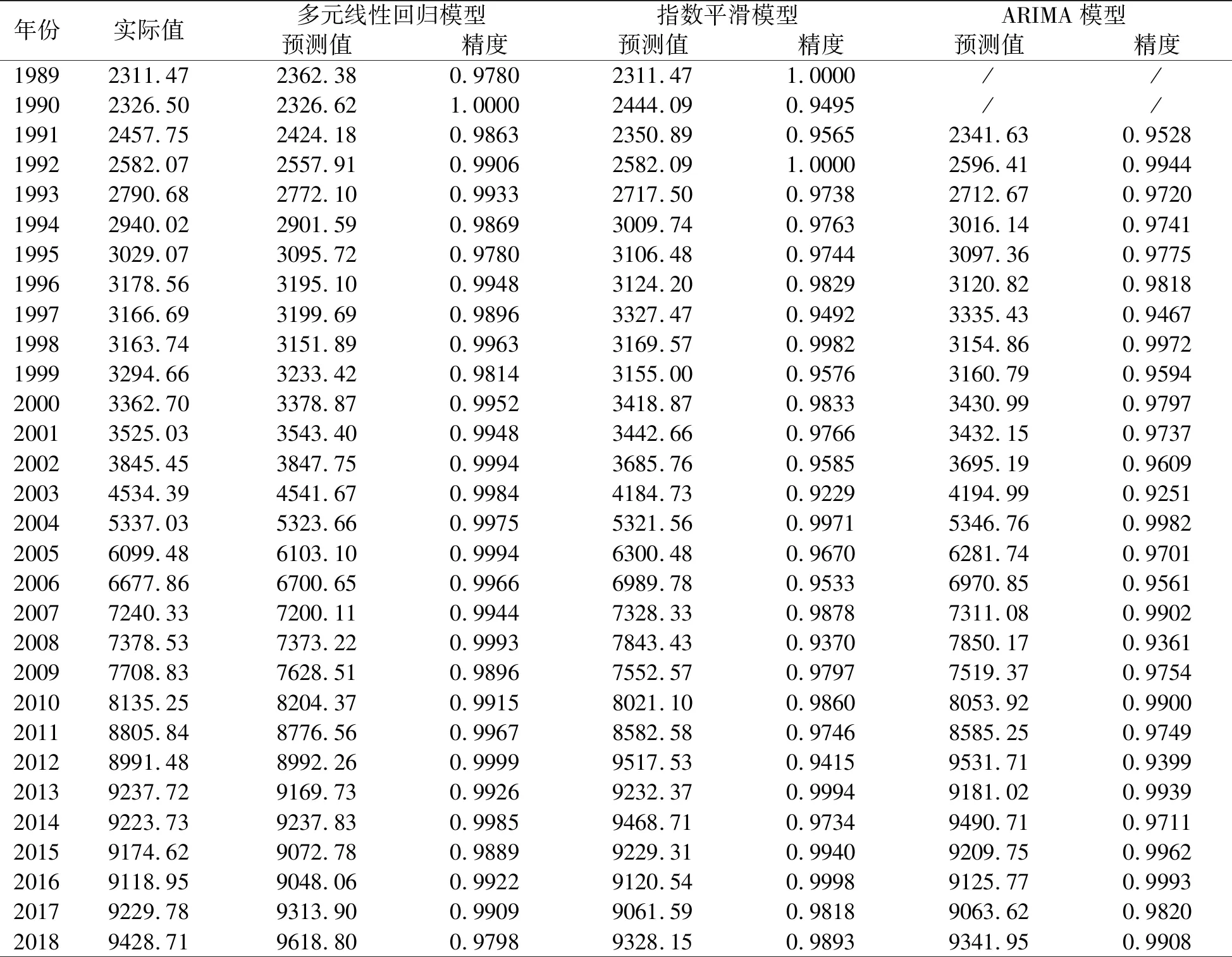
表1 1989—2018年全國碳排放量3種單項預測值和精度

2 基于GIOWA算子的全國碳排放量組合預測模型

2.1 GIOWA組合預測模型的建立

對于碳排放觀測值序列yt>0(t=1,2,…,28)，本文使用多元線性回歸模型、Hlot-Winters 非季節指數平滑和ARIMA三種單項預測模型對其進行預測，設yit為第i種預測方法在第t期預測值，本文將預測值的誘導值設定為預測精度αit，且第i種預測方法第t期的預測精度計算公式為：

(i=1,2,3;t=1,2,…,28)

(5)

將3種單項預測方法在期的預測精度與其對應的預測值可以看做3個二維向量：<α1t,y1t>，<α2t,y2t>，<α3t,y3t> ，將3種單項預測方法在t時刻的預測精度序列α1t，α2t，α3t按照從小到大的順序進行排列，則誘導有序第i種預測模型第t期λ次冪誤差為：

(i=1,2,3;t=1,2,…,28)

(6)

其中，α-index(it)表示誘導有序第i種預測方法的預測精度的下標。

計算樣本期內GIOWA組合預測模型第t期組合預測的λ次冪誤差，公式為：

(7)

其中，w1≥0,w2≥0,w3≥0,w1+w2+w3=1。

計算樣本期內GIOWA組合預測次冪誤差平方和，公式為：

(8)

因此，本文在λ次冪誤差平方和最小的準則下，建立組合預測優化模型：

(9)

計算樣本期間內組合預測模型的預測值，公式為：

(10)

2.2 實證結果與分析

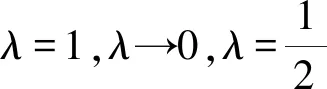
(1)λ=1時廣義誘導有序加權平均(GIOWA)組合預測模型

對應的誘導有序誤差信息矩陣為：

(11)

使預測誤差平方和最小的IOWA組合預測模型為：

(12)

使用LINGO10.0軟件求得權重：w1=0.9660,w2=0,w3=0.0340

得IOWA組合預測模型為：

(13)

樣本期內組合預測誤差平方和：Q=42236.14。

(2)λ→0時廣義誘導有序加權平均(GIOWA)組合預測模型

對應的誘導有序對數誤差信息矩陣為：

(14)

使得對數誤差平方和最小的IOWGA組合預測模型為：

(15)

使用LINGO10.0軟件求得權重：w1=1,w2=0,w3=0

得IOWGA組合預測模型為：

(16)

樣本期內組合預測對數誤差平方和為1.848×10-3。

(17)

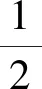
(18)

使用LINGO10.0軟件求得權重：w1=0.9832,w2=0,w3=0.0168

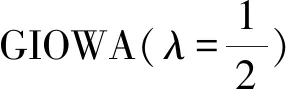
(19)

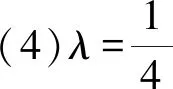
(20)

(21)

使用LINGO10.0軟件求得權重：w1=0.9944,w2=0,w3=0.0056

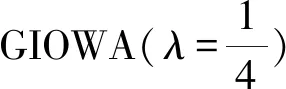
(22)

表2給出了λ取不同值時情況下的廣義誘導有序加權平均組合預測模型的預測值。

表2 取不同值時情況下的GIOWA組合預測模型的預測值

2.3 預測效果評價

為了比較3種單項預測模型和4種GIOWA組合預測模型的有效性，選取以下五個誤差指標作為判斷標準：

(1)平方和誤差(SSE)：

(2)均方根誤差(RMSE)：

(3)平均絕對誤差(MAE)：

(4)平均相對誤差(MAPE)：

(5)均方根相對誤差(RMSRE)

表3給出了所有預測模型的評價指標值以及其歸一化處理結果，并給出了每個模型的平均精度。從表3可以看出，四種GIOWA組合預測模型的各項誤差指標均低于三種單項預測模型，且組合預測模型的平均精度均達到99.4%，高于三種單項預測模型的平均精度，表明基于GIOWA 算子的組合預測模型能夠提高我國碳排放量的預測精度。

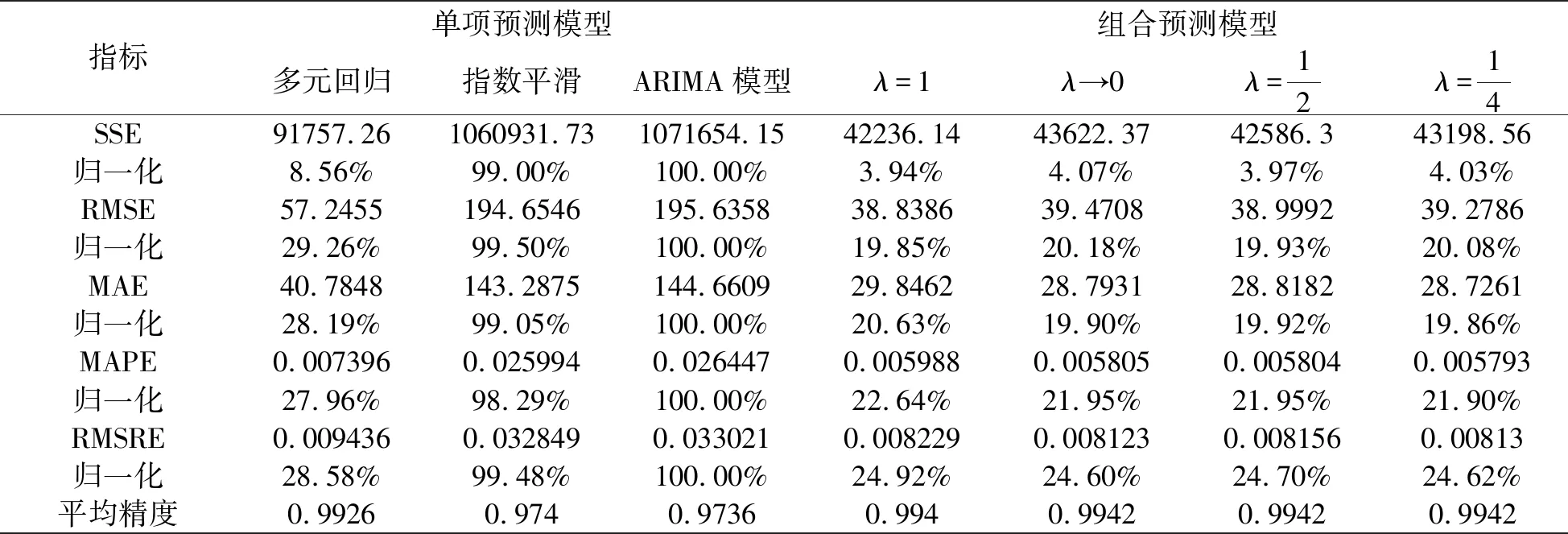
表3 預測效果評價指標體系

2.4 未來五年的碳排放量的預測值

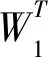
根據三種單項預測模型的權重可以計算我國在2019—2023年間各年的排放量的預測值，具體結果見表4。由表4可以看出，四種組合預測模型的預測結果非常接近，可見具有較高的預測精度。2019—2023年我國碳排放量穩步增長，年均增長速度分別為4.1066%、2.5782%、2.5788%、2.5793%、2.5799%。

表4 2019—2023年我國碳排放量的預測值(單位：百萬噸)

使用Hlot-Winters 非季節指數平滑預測方法對我國2019—2023年間的GDP進行預測，根據GDP和碳排放量的預測值可以計算出我國碳排放強度。2019—2023年間我國碳排放強度呈下降趨勢，年均下降速度分別為3.0996%、4.5222%、4.5217%、4.5212%、4.5207%。

3 結論

本文基于1989-2018年全國的二氧化碳排放量數據，首先，使用多元線性回歸模型、Hlot-Winters 非季節指數平滑模型和ARIMA(0,2,0)三種單項預測模型對我國碳排放量進行預測，其次，以誤差平方和最小為準則，建立基于GIOWA算子的我國碳排放量組合預測模型，并通過預測效果評價指標體系對單項預測模型和組合預測模型的有效性進行比較，研究結果表明：組合預測模型的平均預測精度高于三種單一的預測模型，有效克服了各單項預測模型的缺點；未來五年，我國碳排放總量處于增長趨勢，但是碳排放強度呈下降趨勢。

通過對我國碳排放量進行預測，可以看出我國節能減排任重而道遠，因此，我國需要積極引進國外先進生產技術，加強科技創新，提高能源利用效率，促進清潔能源的開發和使用，從而減少碳排放和推動我國碳排放量在2030年達到峰值目標的實現。