數列通頂問題
一、填空題
1.(2019年全國Ⅰ卷)記Sn為等差數列{an}的前n項和,若a1≠0,a2=3a1,則________.
2.(2019年西安市期中卷)設Sn為數列{an}的前n項和,且a1=-1,an+1=SnSn+1,則Sn=________.
3.將全體正整數排成如下4列數陣:
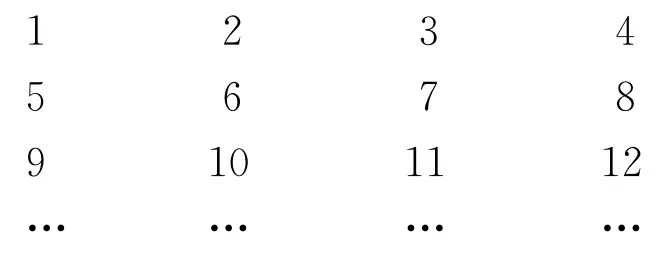
其中cm表示數陣中第m行第3列的數,則cm=________.
4.已知數列{an}對任意的p,q∈N*,滿足ap+q=apaq,且a1=2,則an=________.
5.設集合A={x|x=2n,n∈N*},B={x|x=2n-1,n∈N*},數列{an}即為A∪B中元素從小到大排成的數列,如a1是A∪B中的最小數,則an=________.
6.已知數列{an}的首項為a1=2,且,記Sn為數列{an}的前n項和,則Sn=________.
8.設數列{an}為等差數列,{bn}為等比數列,數列{cn}的前n項和為Sn,且cn=an+bn,若2Sn+2cn=n2+3n+2,則an=________,bn=________.
9.已知正項數列{an}的首項為1,且對于一切正整數n都有an+1,則數列的通項公式是an=________.
10.(2019年讓西師大附中月考卷)定義:稱為n個正數P1,P2,…,Pn的“均倒數”.若數列{an}的前n項的“均倒數”為,則數列{an}的通項公式為________.
二、解答題
11.已知有窮數列{an}共有2k項,其中整數k≥2,前n項和為Sn,且a1=2,Sn=,其中常數a>1.
(1)求數列{Sn}的通項公式;

12.(2019年天津市模擬卷)已知首項為2的數列{an}的前n項和為Sn,若點(an+1,Sn)在函數的圖象上,設bn=log2an.
(1)判斷數列{bn}是否為等差數列,并說明理由;

13.設數列{an},{bn}滿足a1=4,a2=.
(1)證明:an>2,0<bn<2(n∈N*);

14.已知數列{an}的首項.
(2)是否存在互不相等的正整數m,s,n,使m,s,n成等差數列,且am-1,as-1,an-1成等比數列?如果存在,請給出證明;如果不存在,請說明理由.


