輔助函數(shù)，如何構(gòu)造

李 紅 倉萬林

問題1：為什么導(dǎo)數(shù)還可以繼續(xù)求導(dǎo)數(shù)？

問題2：什么情況下要構(gòu)造輔助函數(shù)后再求導(dǎo)？

同學(xué)們，在導(dǎo)數(shù)學(xué)習(xí)時(shí)，你是不是有以上的疑問？

那么，在你的理解中，導(dǎo)數(shù)究竟是什么呢？再來看一下導(dǎo)數(shù)的概念（蘇教版選修2-2第14頁）：

若f(x)對(duì)于區(qū)間內(nèi)任一點(diǎn)都可導(dǎo)，則f(x)在各點(diǎn)的導(dǎo)數(shù)也隨自變量x的變化而變化，因而也是自變量x的函數(shù)，該函數(shù)稱為f(x)的導(dǎo)函數(shù)，記做f'(x).

在不引起混淆時(shí)，導(dǎo)函數(shù)f'(x)也簡(jiǎn)稱為f(x)的導(dǎo)數(shù)．

導(dǎo)數(shù)本身也是一種函數(shù)．既然導(dǎo)數(shù)可以分析函數(shù)的性質(zhì)，當(dāng)然可以對(duì)導(dǎo)數(shù)繼續(xù)求導(dǎo)分析導(dǎo)數(shù)的性質(zhì)了，問題1 是很自然的．

如何有針對(duì)性地構(gòu)造輔助函數(shù)分析其性質(zhì)呢？舉例來看．

例1已知函數(shù)y=f(x)，x∈[0,2π]的導(dǎo)函數(shù)f'(x)的圖象，如圖所示，則y=f(x)的單調(diào)增區(qū)間為________.

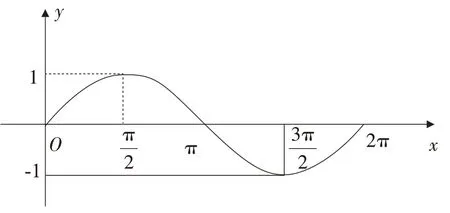
圖1

解析：由圖1 得到，x∈[0,π]時(shí)，f'(x)≥0，故y=f(x)的單調(diào)增區(qū)間為[0,π].

敲黑板

利用導(dǎo)數(shù)分析函數(shù)性質(zhì)時(shí)，常用方法是構(gòu)造輔助函數(shù)．

敲黑板

這個(gè)概念題就曾經(jīng)坑了不少同學(xué)．你掉坑了嗎？

用導(dǎo)數(shù)分析函數(shù)性質(zhì)的問題中，對(duì)于原函數(shù)我們通常分析其單調(diào)性；對(duì)于導(dǎo)函數(shù)，我們一般研究其表達(dá)式的符號(hào)是正還是負(fù)．

例2（2019屆南師附中、天一中學(xué)、海門中學(xué)、淮陰中學(xué)調(diào)研）已知函數(shù)f(x)=的極大值為1．

（1）求m的值；

解析：（1）m=1（過程略）.

所以h(x)在(1,+∞)上單調(diào)遞增，

所以f(x0)＞g(x0)．

以下解題過程請(qǐng)同學(xué)們自行完成.

收納袋

輔助函數(shù)的構(gòu)造：1.抓住核心的總體或者部分結(jié)構(gòu)；2.所構(gòu)造的函數(shù)要易于求導(dǎo)，易于判斷導(dǎo)數(shù)的正負(fù).

本題是用導(dǎo)數(shù)工具分析函數(shù)性質(zhì)的綜合性問題，涉及三個(gè)輔助函數(shù)的構(gòu)造.以輔助函數(shù)1為例來分析.

表1：例2中輔助函數(shù)1構(gòu)造方案比較（x＞1）