中立型隨泛函微分方程解的存在唯一性

何曉瑩

（廣西科技大學理學院，廣西柳州545006）

0 引言

隨機泛函微分方程可看成是泛函微分方程和隨機微分方程的推廣，它不僅取決于系統當前的狀態，還與事物的過去狀態有關，故被廣泛應用于生物、物理、金融、力學、生態學、神經網絡及工程等各領域[1-2].中立型隨機泛函微分方程是隨機泛函微分方程理論中一類重要的方程.它所描述的動力系統不僅依賴于目前的狀態和過去一段時間的狀態，還依賴于過去一段時間狀態的變化率，具有廣泛的應用.

近年來，非線性期望理論受到廣泛的關注.2005年，PENG[3-5]創建了G-期望理論體系，是一種非線性期望.在G-期望框架下，引入了相關的G-正態分布、G-布朗運動和G-Ito?積分.隨之很多文章對G-布朗運動進行了深入研究[6-8].在這個基礎上，文獻[9]研究了G-隨機微分方程解的存在性和唯一性，但中立型隨機泛函微分方程還未涉及.

本文在局部非利普希茨條件下研究G-布朗運動驅動的中立型隨機泛函微分方程（G-NSFEs）解的存在唯一性.

1 預備知識

考慮如下的G-NSFEs：有：

初始值x0=ξ={ξ(θ):-τ≤θ≤0}∈K，xt={x(t+θ):-τ≤θ≤0}為K值隨機過程.D∶K →Rd，f∶[0,T]× K → Rd，g∶[0,T]× K → Rd×m和h∶[0,T]× K→ Rd×m是Borel可測的.

為了證明本文的主要結果，給出如下假設：

假設Ⅰ存在某個函數H(t,u):[0,T]×[0,+∞)→[0,+∞)和κ∈(0,1)，使得對任意t∈[0,T]和x∈K，有：

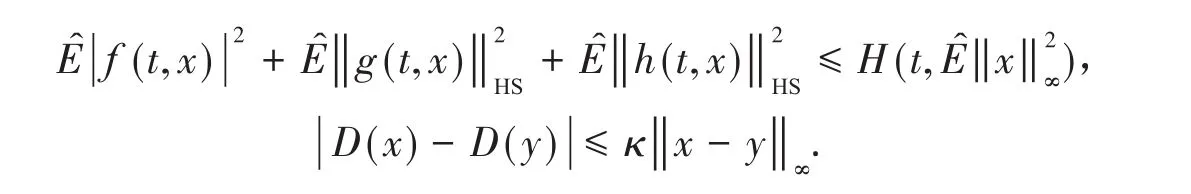
‖?‖HS表示Hilbert-Schmidt范數，其中，對固定的u∈[0,+∞)，函數H(t,u)關于t局部可積；對固定的t∈[0,T]，函數H(t,u)關于u連續且非降；對任意γ＞0，u0≥0，積分方程在[0,T]內有解.

假設Ⅱ存在某個函數G(t,u):[0,T]×[0,+∞)→[0,+∞)，使得對任意t∈[0,T]和x,y∈K，有：

其中：G(t,0)=0，對固定u∈[0,+∞)，函數G(t,u)關于t局部可積；對固定t∈[0,T]，函數G(t,u)關于u連續且非降；對某個常數α＞0，如果存在一個非負連續函數z(t)滿足:

則有z(t)=0.

引理1[7]對p≥1，T≥0和η∈MpG([0,T];Rd)，有:

且對p≥2，存在常數Cp＞0，有：

引理2[10]（Doob鞅不等式） 對p＞1，{x(t)}t≥0是G-鞅和[a,b]是正實數的有界區間，當x∈MGp([0,T];Rd)，存在，有

引理3[11]對于方程其中u(t0)=u0，u0≥0.若H(t,u)滿足假設Ⅰ，則對于任意的γ＞0，方程存在一個局部解.

2 解的存在唯一性

利用Picard迭代法給出方程（1）解的存在唯一性結論.設x0(t)=ξ(0)，對于n=1,2,…，令xn0=ξ，并定義如下迭代序列：

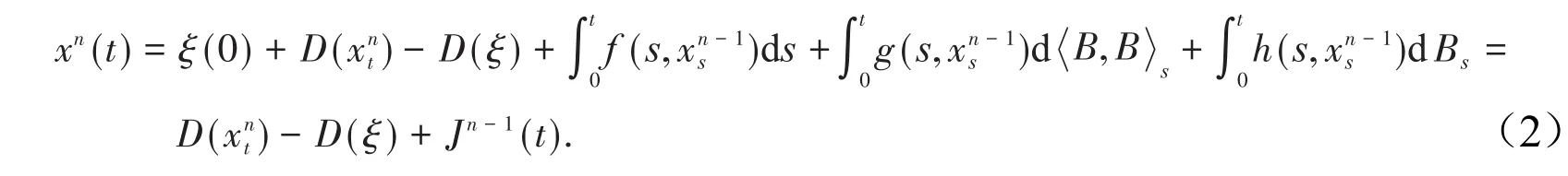
式中：

定理1設{xn(t)}n≥1是式（2）所定義的隨機序列過程，D(x),f(t,x),g(t,x),h(t,x)滿足假設Ⅰ和假設Ⅱ，則對于是一致有界的.

證明由假設Ⅰ，?t∈[0,T]，有：

取u0∈ R+，使得

對式（3）兩邊取上確界和G-期望，可得：

對?t∈[0,T]，有：

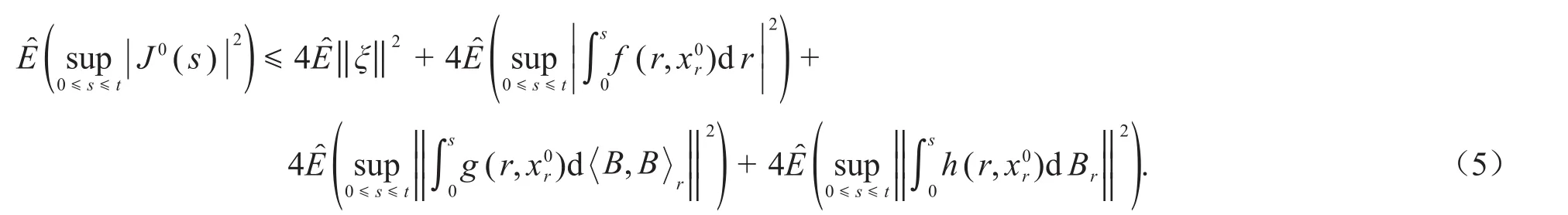
再由引理1和引理2，式（5）化為：

將式（6）代入式（4），由假設Ⅰ有：

這里用到了t≥0和假設Ⅰ中H(t,u(t))關于u(t)是單調非降的.

對式（9）兩邊取上確界和G-期望，有：

由引理1和引理2，可知：

由于函數u(t)在[0,T]上連續，則：

且由假設Ⅰ，H(t,u(t))關于u(t)是單調非降的，故對于t∈[0,T]，H(t,u(t))≤H(t,p0)成立.

將式（11）代入式（10），再由假設Ⅰ和式（12）可得：

假設n=m時，對?t∈[0,T]，下列不等式成立，

則對?t∈[0,T]，類似于式（7）的推論，有：

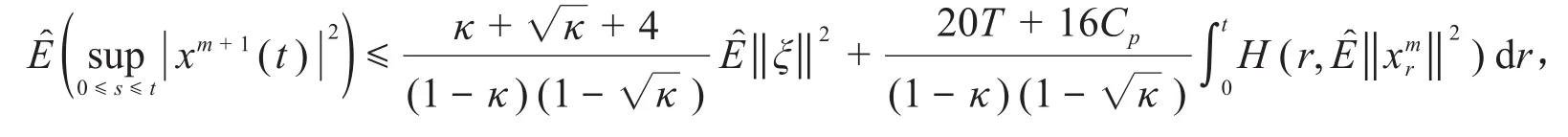
另外，與式（13）類似的推導，可推出：

由于u(t)在[0,T]上連續，故存在常數M ＞0，對?t∈[0,T],n∈N，有定理1證畢.

定理2假設Ⅰ和假設Ⅱ成立，則對?t∈[0,T]，方程（1）存在唯一解.

證明 先證明{xn(t)}n≥1為柯西序列.由式（2）可得：

對式（17）兩邊取上確界和G-期望，有：

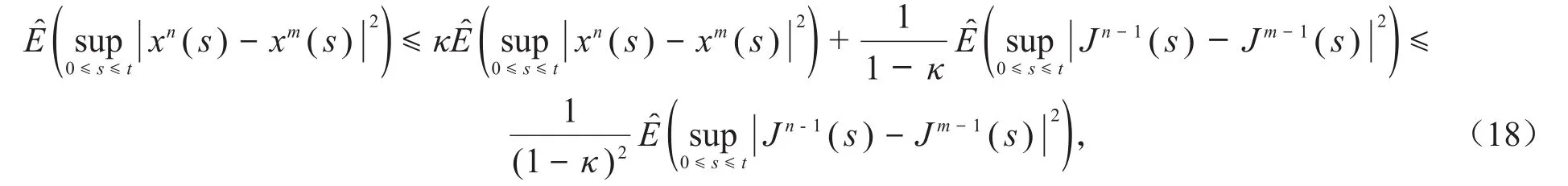
由基本不等式(a+b+c)2≤3a2+3b2+3c2，有：

再由引理1、引理2和假設Ⅱ，可得：

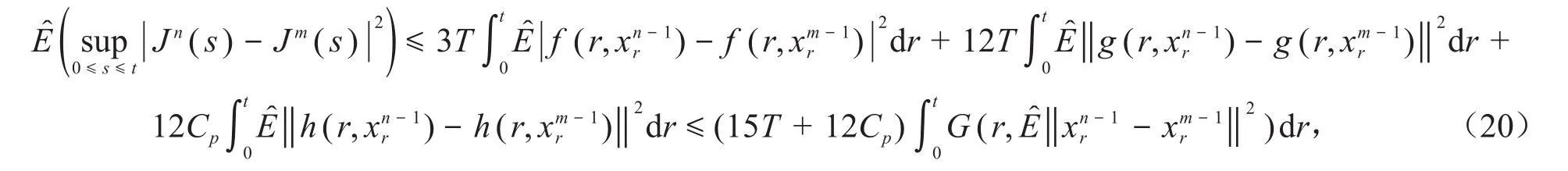
將式（20）代入式（18），可知：

由Fatou引理，可知：

再由假設Ⅱ，有：

由定理1及上述證明可知，對任意固定的T＞0，{xn(t)}是收斂的Cauchy序列.設其極限為x(t).類似于式（21）的推導，有：

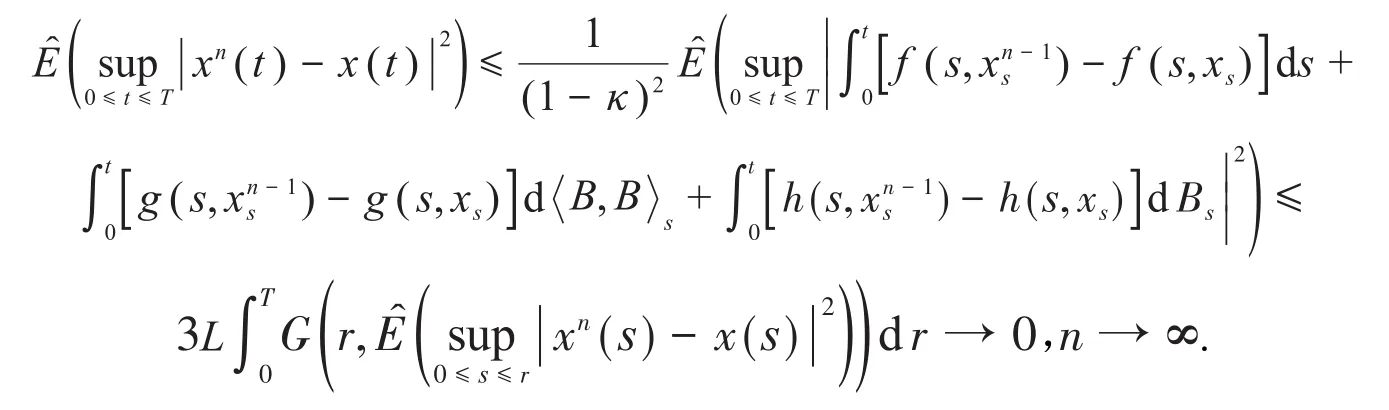
對式（2）兩邊取極限，可知x(t)滿足方程（1），故解的存在性得證.

再證明唯一性.設x(t)和y(t)為方程（1）兩個解，類似式（21）的證明可得：

對?t∈[0,T]，有：

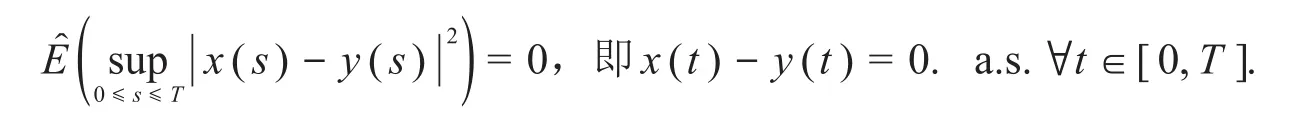
故定理2證畢.