構建立體幾何模型,小議棱錐的外接球問題
◇ 甘肅 茍丫丫
與球相關的切接問題是高考命題的熱點,也是考生理解上的難點、易失分點,命題角度多變,要求學生有較強的空間想象能力,在把握題意的基礎上對要解決的問題有豐富的聯想能力;在解決問題的過程中有良好的平面幾何計算能力.在平時的教學中,教師應利用信息技術演示球的內接幾何體,讓學生有直觀想象的依據.本文就棱錐的外接球問題做如下模型探討.
1 補形法,簡化問題求解
例1球面上有四個點P,A,B,C,滿足PA,PB,PC 兩兩垂直,且PA=3,PB=4,,則球的表面積等于
分析在三棱錐P-ABC 中,棱PA,PB,PC 兩兩互相垂直,是本題解題的題眼.解決立體幾何問題應多觀察,多思考,大膽假設,小心求證.這樣的三棱錐來源于以為長寬高的長方體,它們的外接球是同一個球體,而長方體的外接球問題學生是熟悉的.此時,球的直徑是長方體的體對角線.
解析
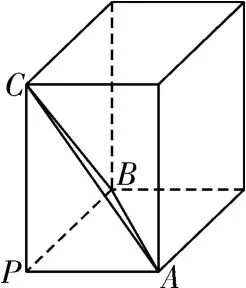
圖1
2 利用對稱中心,直接求解
例2已知S-ABC 為棱長為a 的正四面體,求它的外接球的半徑.
分析正四面體與它的外接球都是中心對稱的幾何體,故正四面體的中心既是它的外接球球心,又是它的內切球球心.如圖2,M 為點S 在平面ABC 上的射影,即為△ABC 的中心,也是重心,球心O 在SM 上.
解析
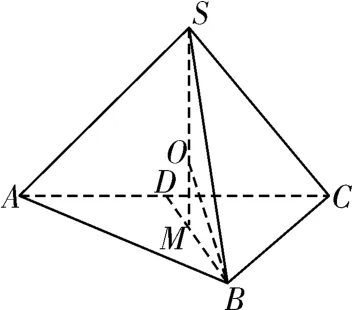
圖2
又有OM2+MB2=OB2,即
例3體積為的正四棱錐S-ABCD 的底面中心為O,SO 與側面成的角的正切值為那么過SABCD 的各頂點的球的表面積是( ).
A.32π B.24π C.16π D.12π
分析設正四棱錐的底面邊長為a,高為h,題設給出了正四面體的體積,有又給出SO 與側面成的角的正切值為是底面邊長a 和高h 的第二個關系式.根據兩個條件,可求出底面邊長a和高h,再去解決它的外接球問題.
解析
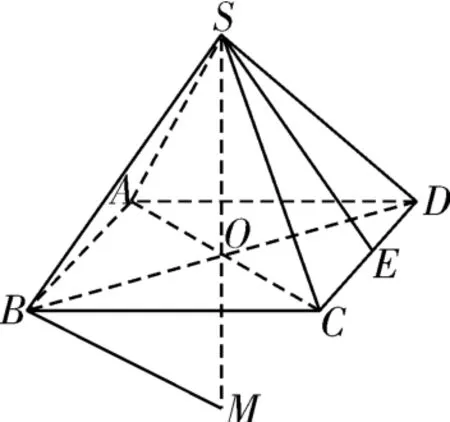
圖3
方法1延長SO 交球面于點M,則S,B,M 均在球面上,且SM=2R,∠SBM=90°.
在Rt△SMB 中,由射影定理得
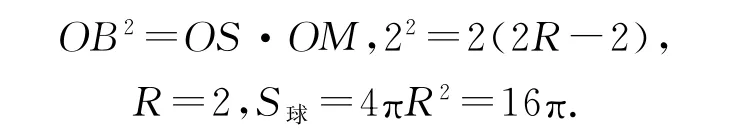
方法2同例2的解法,可得=4πR2=16π.
3 類比圓的性質,轉化問題求解
例4如圖4,在平面四邊形ABCD 中,AB=將其沿對角線BD折成四面體A′-BCD,使面A′BD⊥面BCD,若四面體A′-BCD 的頂點在同一球面上,則該球的表面積為( ).
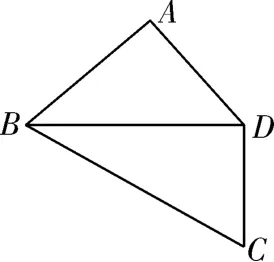
圖4
分析先根據題意,得出折疊后四面體的特征,再解決它的外接球問題.
解析
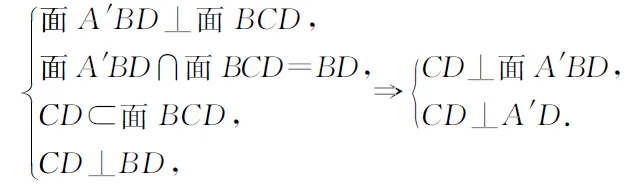
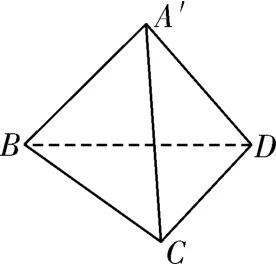
圖5
類比圓,直徑所對的圓周角為直角,那么內接于球的A′-BCD 中,BC 所對的兩個角都是直角,故BC為球的直徑.所以
點評
對于不同于例1、例2的四面體的外接球問題,要通過認真審題,研讀題意,大膽猜想,小心論證,抓住特征,解決問題.
雖然棱錐的外接球問題題型多變,但只要抓住問題的實質,透過現象看本質,就能找出棱錐的特征,還是可類比圓的內接三角形問題.只有細心研讀題意,緊密聯系生活實際,正確歸類問題,建立恰當的數學模型,才能順利解決問題!

